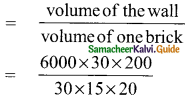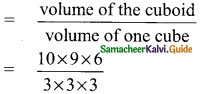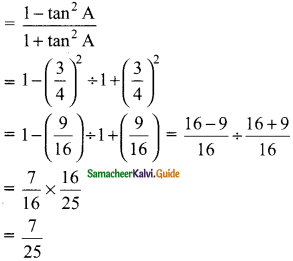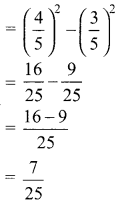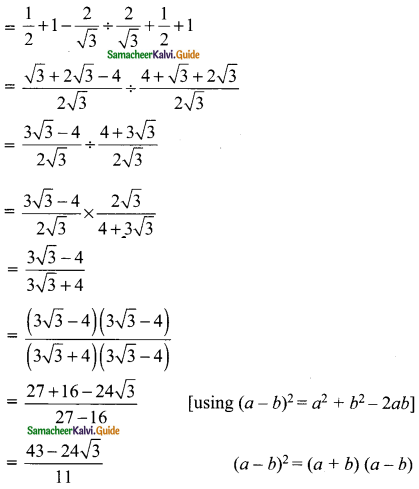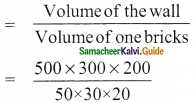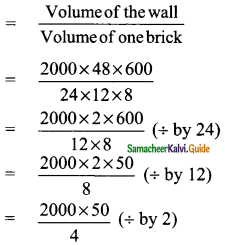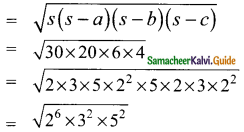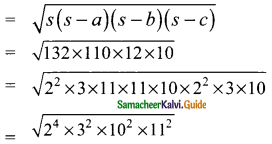Category: Class 9

Students can download Maths Chapter 1 Set Language Ex 1.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.3

Question 1.
Using the given venn diagram, write the elements of

(i) A
(ii) B
(iii) A∪B
(iv) A∩B
(v) A – B
(vi) B – A
(vii) A’
(viii) B’
(ix) U
Solution:
(i) A = {2, 4, 7, 8, 10}
(ii) B = {3, 4, 6, 7, 9, 11}
(iii) A∪B = {2, 3, 4, 6, 7, 8, 9, 10, 11}
(iv) A∩B = {4, 7}
(v) A – B = {2, 8, 10}
(vi) B – A = {3, 6, 9, 11}
(vii) A’ = {1, 3, 6, 9, 11, 12}
(viii) B’ = {1,2, 8, 10, 12}
(ix) U = {1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12}

Question 2.
Find A∪B, A∩B, A – B and B – A for the following sets
(i) A = {2, 6, 10, 14} and B = {2, 5, 14, 16}
Solution:
A∪B = {2, 6, 10, 14} ∪ {2, 5, 14, 16}
= {2, 5, 6, 10, 14, 16}
A∩B = {2, 6, 10, 14} ∩ {2, 5, 14, 16}
= {2, 14}
A – B = {2, 6, 10, 14} – {2, 5, 14, 16}
= {6, 10}
B – A = {2, 5, 14, 16} – {2, 6, 10, 14}
= {5, 16}

(ii) A = {a, b, c, e, u} and B = {a, e, i, o, u}
Solution:
A∪B = {a, b, c, e, u} ∪ {a, e, i, o, u}
= {a, b, c, e, i, o, u}
A∩B = {a, b, c, e, u} ∩ {a, e, i, o, u}
= {a, e, u}
A – B = {a, b, c, e, u} – {a, e, i, o, u}
= {b, c}
B – A = {a, e, i, o, u} – {a, b, c, e, u}
= {i, o}

(iii) A = {x : x ∈ N, x ≤ 10} and B = {x : x ∈ W, x < 6}
Solution:
A = {1, 2, 3, 4, 5, 6,7, 8, 9, 10} and B = {0, 1, 2, 3, 4, 5}
A∪B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} ∪ {0, 1, 2, 3, 4, 5}
= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A∩B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} ∩ {0, 1, 2, 3, 4, 5}
= {1, 2, 3, 4, 5}
A – B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} – {0, 1, 2, 3, 4, 5}
= {6, 7, 8, 9, 10}
B – A = {0, 1, 2, 3, 4, 5} – {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
= {0}

(iv) A = Set of all letters in the word “mathematics” and B = Set of all letters in the word “geometry”
Solution:
A = {m, a, t, h, e, i, c, s}
B = {g, e, o, m, t, r, y}
A∪B = {m, a, t, h, e, i, c, s} ∪ {g, e, o, m, t, r, y}
= {a, c, e, g, h, i, m, o, r, s, t, y}
A∩B= {m, a, t, h, e, i, c, s} ∩ {g, e, o, m, t, r, y}
= {e, m, t}
A – B = {m, a, t, h, e, i, c, 5} – {g, e, o, m, t, r, y}
= {a, c, h, i, s}
B -A = {g, e, o, m, t, r, y} – {m, a, t, h, e, i, c, s}
= {g, o, r, y}

Question 3.
If U = {a, b, c, d, e, f, g, h), A = {b, d, f, h} and B = {a, d, e, h}, find the following sets.
(i) A’
Solution:
A’ = U – A
= {a, b, c, d, e, f, g, h} – {b, d, f, h)
= {a, c, e, g}

(ii) B’
Solution:
B’ = U – B
= {a, b, c, d, e, f, g, h} – {a, d, e, h}
= {b, c, f, g}

(iii) A’∪B’
Solution:
A’∪B’ = {a, c, e, g} ∪ {b, c,f, g}
= {a, b, c, e, f, g}

(iv) A’∩B’
Solution:
A’∩B’ = {a, c, e, g} ∩ {b, c, f, g}
= {c, g}

(v) (A∪B)’
Solution:
A∪B = {b, d, f, h} ∪ {a, d, e, h}
= {a, b, d, e, f, h}
(A∪B)’ = U – (A∪B)
= {a, b, c, d, e, f, g, h} – {a, b, d, e, f, h}
= {c, g}

(vi) (A∩B)’
Solution:
(A∩B) = {b, d, f, h) ∩ {a, d, e, h)
= {d, h}
(A∩B)’ = U – (A∩B)
= {a, b, c, d, e, f, g, h} – {d, h}
= {a, b, c, e, f, g}

(vii) (A’)’
Solution:
A’ = {a, c, e, g}
(A’)’ = U – A’
= {a, b, c, d, e, f, g, h} – {a, c, e, g}
= {b, d, f, h}

(viii) (B’)’
Solution:
B’ = {b, c, f, g}
(B’)’ = U – B’
= {a, b, c, d, e, f, g, h) – {b, c, f, g)
= {a, d, e, h}

Question 4.
Let U = {0, 1, 2, 3, 4, 5, 6, 7} A = {1, 3, 5, 7} and B = {0, 2, 3, 5, 7}, find the following sets.
(i) A’
Solution:
A’ = U – A
= {0, 1, 2, 3, 4, 5, 6, 7} – {1, 3, 5, 7}
= {0, 2, 4, 6}

(ii) B’ = U – B
Solution:
= {0, 1, 2, 3, 4, 5, 6, 7} – {0, 2, 3, 5, 7}
= {1, 4, 6}

(iii) A’∪B’
Solution:
A’∪B’ = {0, 2, 4, 6,}∪{1, 4, 6}
{0, 1, 2, 4, 6}

(iv) A’∩B’
Solution:
A’∩B’ = {0, 2, 4, 6,}∩{1, 4, 6}
{4, 6}

(v) (A∪B)’
Solution:
A∪B = {1, 3, 5, 7}∪{0, 2, 3, 5, 7}
= {0, 1, 2, 3, 5, 7}
(A∪B)’ = U – (A∪B)
{0, 1, 2, 3, 4, 5, 6, 7} – {0, 1, 2, 3, 5, 7}
{4, 6}

(vi) (A∩B)’
Solution:
(A∩B)= {1, 3, 5, 7}∩{0, 2, 3, 5, 7}
= {3, 5, 7}
(A∩B)’ = U – (A∩B)
= {0, 1, 2, 3, 4, 5, 6, 7} – {3, 5, 7}
= {0, 1, 2, 4, 6}

(vii) (A’)’
A’ = {0, 2, 4, 6}
(A’)’ = U – A’
= {0, 1, 2, 3, 4, 5, 6, 7} – {0, 2, 4, 6}
= {1, 3, 5, 7}

(viii) (B’)’
B’ = {1, 4, 6}
(B’)’ = {0, 1, 2, 3, 4, 5, 6, 7} – {1, 4, 6}
= {0, 2, 3, 5, 7}

Question 5.
Find the symmetric difference between the following sets.
(i) P = {2, 3, 5, 7, 11} and Q = {1, 3, 5, 11}
Solution:
Use anyone of the formula to find A & B
AΔB = (A – B)∪(B – A) or AΔB = (A∪B) – (A∩B)
P∪Q = {2, 3, 5, 7, 11} ∪ {1,3,5, 11}
= {1, 2, 3, 5, 7, 11}
P∩Q = {2, 3, 5, 7, 11}∩{1, 3, 5,11}
= {3, 5, 11}
PΔQ = (P∪Q) – (P∩Q)
= {1, 2, 3, 5, 7, 11} – {3, 5, 11}
= {1, 2, 7}
(OR)
P – Q = {2, 3, 5, 7, 11} – {1, 3, 5, 11}
= {2,7}
Q – P = {1, 3, 5, 11} – {2, 3, 5, 7, 11}
= {1}
PΔQ = (P – Q)∪(Q – P)
= {2, 7} ∪ {1}
= {1, 2, 7}

(ii) R = {l, m, n, o, p} and S = {j, l, n, q}
Solution:
R- S = {l, m, n, o, p} – {j, l, n, q}
= {m, o, p}
S – R = {j, l, n, q} – {l, m, n, o, p}
= {j, q}
RΔS = (R – S)∪(S – R)
= {m, o, p} – {j, q} = {j, m, o, p, q)
(OR)
R∪S = {l, m, n, o, p} ∪ {j,l,n,q}
= {l, m, n, o, p, j, q}
R∩S = {l, m, n, o,p} ∩ {j, l, n, q}
= {l, n}
RΔS = (R∪S) – (R∩S)
= {l, m, n, o, p, j, q} – { l, n}
= {m, o, p, j, q}

(iii) X = {5, 6, 7} and Y = {5, 7, 9, 10}
Solution:
X∪Y = {5, 6, 7} ∪ {5, 7, 9, 10}
= {5 ,6, 7, 9, 10}
X∩Y = {5, 6, 7} ∩ {5, 7, 9, 10}
= {5, 7}
XΔY = (X∪Y) – (X∩Y)
= {5, 6, 7, 9, 10} – {5, 7}
= {6, 9, 10}
OR
X – Y = {5, 6, 7} – {5, 7, 9, 10} = {6}
Y – X = {5, 7, 9, 10} – {5, 6, 7} = {9, 10}
XΔY = (X – Y) ∪ (Y – X)
= {6}∪{9, 10}
= {6, 9, 10}

Question 6.
Using the set symbols, write down the expressions for the shaded region in the following

Solution:

Question 7.
Let A and B be two overlapping sets and the universal set U. Draw appropriate Venn diagram for each of the following,
(i) A∪B
(ii) A∩B
(iii) (A∩B)’
(iv) (B – A)’
(v) A’∪B’
(Vi) A’∩B’
(vii) What do you observe from the Venn diagram (iii) and (v)?
Solution:
(i) A∪B

(ii) A∩B

(iii) (A∩B)’

(iv) (B – A)’

(v) A’∪B’

(Vi) A’∩B’

(vii) What do you observe from the diagram (iii) and (v)?
From the diagram (iii) and (v) we get (A∩B)’ = A’∪B’

Students can download Maths Chapter 3 Algebra Ex 3.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.3

Question 1.
Check whether p(x) is a multiple of g(x) or not.
(i) p(x) = x³ – 5x² + 4x – 3; g(x) = x – 2
Solution:
p(x) = x³ – 5x² + 4x – 3
P(2) = (2)³ – 5(2)² + 4(2) – 3
= 8 – 5(4) + 8 – 3
= 8 – 20 + 8 – 3
= 16 – 23
= -7
p{2) ≠ 0
∴ p(x) is not a multiple of g(x)

Question 2.
By remainder theorem, find the remainder when p(x) is divided by g(x) where,
(i) p(x) = x³ – 2x² – 4x – 1; g(x) = x + 1
Solution:
p(x) = x³ – 2x² – 4x – 1
p(-1) = (-1)³ – 2(-1)² – 4(-1) – 1
= 1 – 2 + 4 – 1
= 4 – 4 = 0
∴ The remainder = 0

(ii) p(x) = 4x³ – 12x² + 14x – 3; g(x) = 2x – 1
Solution:
p(x) = 4x³ – 12x² + 14x – 3

= 4 × \(\frac{1}{8}\) – 12 × \(\frac{1}{4}\) + 14 × \(\frac{1}{2}\) – 3
= \(\frac{1}{2}\) – 3 + 7 – 3
= \(\frac{1}{2}\) – 6 + 7
= \(\frac{1}{2}\) + 1
= \(\frac{3}{2}\)
∴ The reminder is \(\frac{3}{2}\)

(iii) p(x) = x³ – 3x² + 4x + 50; g(x) = x – 3
Solution:
p(x) = x³ – 3x² + 4x + 50
p(3) = 3³ – 3(3)² + 4(3) + 50
= 27 – 27 + 12 + 50
= 62
The remainder is 62.

Question 3.
Find the remainder when 3x³ – 4x² + 7x – 5 is divided by (x + 3)
Solution:
p(x) = 3x³ – 4x² + 7x – 5
When it is divided by x +3,
p(-3) = 3(-3)³ – 4(-3)² + 7(-3) – 5
= 3(-27) – 4(9) – 21 – 5
= -81 – 36 – 21 – 5
= -143
The remainder is -143.

Question 4.
What is the remainder when x²⁰¹⁸ + 2018 is divided by x – 1.
Solution:
p(x) = x²⁰¹⁸ + 2018
When it is divided by x – 1,
p(1) = 1²⁰¹⁸ + 2018
= 1 + 2018
= 2019
The remainder is 2019.

Question 5.
For what value of k is the polynomial
p(x) = 2x³ – kx² + 3x + 10 exactly divisible by x – 2
Solution:
p(x) = 2x³ – kx² + 3x + 10
When it is exactly divided by x – 2,
P(2) = 0
2(2)³ – k(2)² + 3(2) + 10 = 0
2(8) – k(4) + 6 + 10 = 0
16 – k(4) + 6 + 10 = 0
16 – 4k + 6 + 10 = 0
32 – 4k = 0
32 = 4k
∴ k = \(\frac{32}{4}\)
= 8
The value of k = 8

Question 6.
If two polynomials 2x³ + ax² + 4x – 12 and x³ + x² – 2x + a leave the same remainder when divided by (x – 3), find the value of a and also find the remainder.
Solution:
p(x₁) = 2x³ + ax² + 4x – 12
When it is divided by x – 3,
p(3) = 2(3)³ + a(3)² + 4(3) – 12
= 54 + 9a + 12 – 12
= 54 + 9a ……….(R₁)
p(x₂) = x³ + x² – 2x + a
When it is divided by x – 3,
p(3) = 3³ + 3² – 2(3) + a
= 27 + 9 – 6 + a
= 30 + a ………(R₂)
The given remainders are same (R₁ = R₂)
∴ 54 + 9a = 30 + a
9a – a = 30 – 54
8a = -24
∴ a = -24/8
= -3
Consider R₂,
Remainder = 30 – 3
= 27

Question 7.
Determine whether (x – 1) is a factor of the following polynomials:
(i) x³ + 5x² – 10x + 4
Solution:
p(x) = x³ + 5x² – 10x + 4
p(1) = 1³ + 5(1) – 10(1) + 4
= 1 + 5 – 10 + 4
= 10 – 10
= 0
∴ x – 1 is a factor of p(x)

(ii) x⁴ + 5x² – 5x + 1
Solution:
p(1) = 1⁴ + 5(1)² – 5(1) + 1
= 1 + 5 – 5 + 1
= 7 – 5
= 2
= 0
∴ x – 1 is not a factor of p(x)

Question 8.
Using factor theorem, show that (x – 5) is a factor of the polynomial
2x³ – 5x² – 28x + 15
Solution:
p(x) = 2x³ – 5x² – 28x + 15
x – 5 is a factor
p(5) = 2(5)³ – 5(5)² – 28(5) + 15
= 250 – 125 – 140 + 15
= 265 – 265
= 0
∴ x – 5 is a factor of p(x)

Question 9.
Determine the value of m, if (x + 3) is a factor of x³ – 3x² – mx + 24.
Solution:
p(x) = x³ – 3x² – mx + 24
when x + 3 is a factor
P(-3) = 0
(-3)³ – 3(-3)² – m(-3) + 24 = 0
-27 – 27 + 3m + 24 = 0
-54 + 24 + 3m = 0
-30 + 3m = 0
3m = 30
m = \(\frac{30}{3}\)
= 10
The value of m = 10

Question 10.
If both (x-2) and (x – \(\frac{1}{2}\)) are the factors of ax² + 5x + b, then show that a = b.
Solution:
p(x) = ax² + 5x + b
when (x-2) is a factor
P(2) = 0
a(2)² + 5(2) + b = 0
4a + 10 + b = 0
4a + b = -10 …….(1)
when (x – \(\frac{1}{2}\)) is a factor
p(\(\frac{1}{2}\)) = 0
a\((\frac{1}{2})^2\) + 5(\(\frac{1}{2}\)) + b = 0
Multiply by 4
a + 10 + 4b = 0
a + 46 = -10 …….(2)
From (1) and (2) we get
4a + b = a + 4b
4a – a = 4b – b
3a = 3b
a = b
Hence it is proved.

Question 11.
If (x – 1) divides the polynomial kx³ – 2x² + 25x – 26 without remainder, then find the value of k.
Solution:
p(x) = kx³ – 2x² + 25x – 26
When it is divided by x – 1
P(1) = 0
k(1)³ – 2(1)² + 25(1) – 26 = 0
k – 2 + 25 – 26 = 0
k + 25 – 28 = 0
k – 3 = 0
k = 3
The value of k = 3

Question 12.
Check if (x + 2) and (x – 4) are the sides of a rectangle whose area is x² – 2x – 8 by using factor theorem.
Solution:
Let the area of a rectangle be p(x)
p(x) = x² – 2x – 8
When x + 2 is the side of the rectangle
p(-2) = (-2)² – 2(-2) – 8
= 4 + 4 – 8
= 8 – 8
= 0
When x – 4 is the side of the rectangle.
P(4) = (4)² – 2(4) – 8
= 16 – 8 – 8
= 16 – 16
= 0
(x + 2) and (x – 4) are the sides of a rectangle

Students can download Maths Chapter 3 Algebra Ex 3.6 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.6

Question 1.
Factorise the following.
(i) x² + 10x + 24
Solution:
Product = 24, sum = 10

Split the middle term as 6x and 4x
x² + 10x + 24 = x² + 6x + 4x + 24
= x(x + 6) + 4 (x + 6)
= (x + 6) (x + 4)

(ii) z² + 4z – 12
Solution:
Product = -12, sum = 4

Split the middle term as 6z and -2z
z² + 4z – 12 = z² + 6z – 2z – 12
= z(z + 6) – 2 (z + 6)
= (z + 6) (z – 2)

(iii) p² – 6p – 16
Solution:
Product = -16, sum = -6

Split the middle term as – 8p and 2p
p² – 6p – 16 = p² – 8p + 2p – 16
= p(p – 8) + 2 (p – 8)
= (p – 8) (p + 2)

(iv) t² + 72 – 17t
Solution:
Product = +72, sum = -17

Split the middle term as -9t and -8t
t² – 17t + 72 = t² – 91 – 8t + 72
= t(t – 9) – 8 (l – 9)
= (t – 9) (t – 8)

(v) y² – 16y – 80
Solution:
Product = -80, sum = -16

Split the middle term as -20y and 4y
y² – 16y – 80 = y² – 20y + Ay – 80
= y(y – 20) + 4 (y – 20)
= (y – 20) (y + 4)

(vi) a² + 10a – 600
Solution:
Product = -600, sum =10

Split the middle term as 30a and -20a
a² + 10a – 600 = a² + 30a – 20a – 600
= a(a + 30) – 20 (a + 30)
= (a + 30) (a – 20)

Question 2.
Factorise the following.
(i) 2a² + 9a + 10
Solution:
Product = 2 × 10 = 20, sum = 9

Split the middle term as 5a and 4a
2a² + 9a + 10 = 2a² + 5a + 4a + 10
= a(2a + 5) + 2 (2a + 5)
= (2a+ 5) (a+ 2)

(ii) 5x² – 29xy – 42y²
Solution:
Product = 5 × -42 = -210, sum = -29

Split the middle term as -35x and 6x
5x² – 29xy – 42y² = 5x² – 35xy + 6xy – 42y²
= 5x (x – 7y) + 6y (x – 7y)
= (x – 7y) (5x + 6y)

(iii) 9 – 18x + 8x²
Solution:
Product = 9 × 8 = 72, sum = -18

Split the middle term as -12x and -6x
9 – 18x + 8x² = 8x² – 18x + 9
= 8x² – 12x – 6x + 9
= 4x (2x – 3) – 3 (2x – 3)
= (2x – 3) (4x – 3)

(iv) 6x² + 16xy + 8y²
Solution:
Product = 6 × 8 = 48, sum = 16

Split the middle term as 4xy and 12xy
6x² + 16xy + 8y² = 6x² + 12xy + 4xy + 8y²
= 6x (x + 2y) + 4y(x + 2y)
= (x + 2y) (6x + 4y)
= 2(x + 2y) (3x + 2y)

(v) 12x² + 36x²y + 27y²x²
Solution:
3x²2 [4 + 12y + 9y²]
= 3x² [9y² + 12y + 4]
Product = 9 x 4 = 36, sum =12

Split the middle term as 6y and 6y
12x² + 36x²y + 21y²x² = 3x² [9y² + 12y + 4]
= 3x² [9y² + 6y + 6y + 4]
= 3x² [3y(3y + 2) + 2(3y + 2)]
= 3x² (3y + 2) (3y + 2)
= 3x² (3y + 2)2

(vi) (a + b)² + 9 (a + b) + 18
Solution:
Let (a + b) = x
x² + 9x + 18
Product =18, sum = 9
Split the middle term as 6x and 3x
x² + 9x + 18 = x² + 6x + 3x + 18
= x (x + 6) + 3 (x + 6)
= (x + 6) (x + 3)
But x = a + b
(a + b)² + 9(a + b) + 18 = (a + b + 6) (a + b + 3)

Question 3.
Factorise the following.
(i) (p – q)² – 6(p – q) – 16
Solution:
Let (p – q) = x
(p – q)² – 6 (p – q) – 16 = x² – 6x – 16
Product = -16, sum = -6

Split the middle term as -8x and 2x
x² – 6x – 16 = x² – 8x + 2x – 16
= x(x – 8) + 2(x – 8)
= (x – 8) (x + 2)
(But x = p – q)
= (p – q – 8) (p – q + 2)

(ii) m² + 2mn – 24n²
Solution:
Product = -24, sum = 2

Split the middle term as 6mn and -4mn
m² + 2mn – 24m² = m² + 6mn – 4mn – 24n²
= m(m + 6n) – 4n (m + 6n)
= (m + 6n) (m – 4n)

(iii) √5 a² + 2a – 3√5?
Solution:
Product = √5 × – 3√5 = -15, sum = 2

Split the middle term as 5x and -3x
√5 a² + 2a – 3√5 = √5a² + 5a – 3a – 3√5
= √5 a(a + √5) – 3(a + √5)
= (a + √5) (√5a – 3)

(iv) a⁴ – 3a² + 2
Solution:
Let a² = x
a⁴ – 3a² + 2 = (a²)² – 3a² + 2
= x² – 3x + 2
Product = 2 and sum = -3

Split the middle term as -x and -2x
x² – 3x + 2 = x² – x – 2x + 2
= x(x – 1) – 2(x – 1)
= (x – 1) (x – 2)
a⁴ – 3a² + 2 = (a² – 1)(a² – 2) [But a² = x]
= (a + 1) (a – 1) (a² – 2)

(v) 8m³ – 2m²n – 15mn²
Solution:
8m³ – 2m²n – 15mn² = m(8m² – 2mn – 15n²)
Product = 8(-15) = -120 and sum = -2

Split the middle term as -12mn and 10mn
8m³ – 2m²n – 15mn² = m[8m² – 2mn – 15n²]
= m[8m²– 12mn + 10mn- 15n²]
= m[4m (2m – 3n) + 5n(2m – 3n)]
= m(2m – 3n) (4m + 5n)

(vi) \(\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{2}{x y}\)
Solution:

Students can download Maths Chapter 3 Algebra Ex 3.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.2

Question 1.
Find the value of the polynomial f(y) = 6y – 3y² + 3 at
(i) y = 1
(ii) y = -1
(iii) y = 0
Solution:
(i) When y = 1
f(y) = 6y – 3y² + 3
f(1) = 6(1) – 3(1)² + 3
= 6 – 3 + 3 = 6

(ii) When y = – 1
f(y) = 6y – 3y² + 3
f(-1) = 6(-1) – 3(-1)² + 3
= – 6 – 3 + 3
= – 6

(iii) When y = 0
f(y) = 6y – 3y² + 3
f(0) = 6(0) – 3(0)² + 3
= 0 – 0 + 3
= 3

Question 2.
If p(x) = x² – 2√2x + 1, find p(2√2).
Solution:
p(x) = x² – 2√2x + 1
p(2√2) = (2√2)² – 2√2 (2√2) + 1
= 8 – 8 + 1
= 0 + 1
= 1

Question 3.
Find the zeros of the polynomial in each of the following.
(i) P(x) = x – 3
Solution:
p( 3) = 3 – 3
= 0
p(3) is the zero of p(x)

(ii) p(x) = 2x + 5
Solution:

= -5 + 5
= 2(0)
= 0
Hence –\(\frac{5}{2}\) is the zero of p(x).

(iii) q(y) = 2y – 3
Solution:

= 2 × 0
= 0
Hence \(\frac{3}{2}\) is the zero of q(y).

(iv) f(z) = 8z
Solution:
f(0) = 8 × 0
= 0
Hence 0 is the zero of f(z)

(v) p(x) = ax when a ≠ 0
Solution:
p(0) = a(0)
= 0
Hence, 0 is the zero of p(x)

(vi) h(x) = ax + b, a ≠ 0, a, b∈R
Solution:

Hence –\(\frac{b}{a}\) is the zero of h(x).

Question 4.
Find the roots of the polynomial equations.
(i) 5x – 6 = 0
Solution:
5x = 6
x = \(\frac{6}{5}\)
\(\frac{6}{5}\) is the root of the polynomial.

(ii) x + 3 = 0
Solution:
x = -3
-3 is the root of the polynomial.

(iii) 10x + 9 = 0
Solution:
10x = -9
x = –\(\frac{9}{10}\)
–\(\frac{9}{10}\) is the root of the polynomial.

(iv) 9x – 4 = 0
Solution:
9x = 4
x = \(\frac{4}{9}\)
\(\frac{4}{9}\) is the root of the polynomial.

Question 5.
Verify whether the following are zeros of the polynomial, indicated against them,or not.
(i) p(x) = 2x – 1, x = \(\frac{1}{2}\)
Solution:
p (\(\frac{1}{2}\)) = 2(\(\frac{1}{2}\)) – 1
= 1 – 1
= 0
∴ \(\frac{1}{2}\) is the zero of the polynomial.

(ii) p(x) = x³ – 1, x = 1
Solution:
p(1) = 1³ – 1
= 1 – 1
= 0
∴ 1 is the zero of the polynomial

(iii) p(x) = ax + b, x = \(\frac{-b}{a}\)
Solution:
p(\(\frac{-b}{a}\)) = a(\(\frac{-b}{a}\)) + b
= -b + b
= 0
∴ \(\frac{-b}{a}\) is the zero of the polynomial. a

(iv) p(x) = (x + 3) (x – 4); x = -3, x = 4
Solution:
P(-3) = (-3 + 3) (-3 – 4)
= (0) (-7)
= 0
P( 4) = (4 + 3) (4 – 4)
= (7) (0)
= 0
∴ -3 and 4 are the zeros of the polynomial.

Question 6.
Find the number of zeros of the following polynomials represented by their graphs.

Solution:
(i) Number of zeros = 2 (The curve is intersecting the x-axis at 2 points)
(ii) Number of zeros = 3 (The curve is intersecting the x-axis at 3 points)
(iii) Number of zeros = 0 (The curve is not intersecting the x-axis)
(iv) Number of zeros = 1 (The curve is intersecting at the origin)
(v) Number of zeros = 1 (The curve is intersecting the x-axis at one point)

Students can download Maths Chapter 3 Algebra Ex 3.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.4

Question 1.
Expand the following:
(i) (2x + 3y + 4z)²
(ii) (-p + 2q + 3r)²
(iii) (2p + 3) (2p – 4) (2p – 5)
(iv) (3a + 1) (3a – 2) (3a + 4)
Solution:
We know that (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac
(i) (2x + 3y + 4z)² = (2x)² + (3y)² + (4z)² + 2(2x) (3y) + 2(3y) (4z) + 2(4z) (2x)
= 4x² + 9y² + 16z² + 12xy + 24yz + 16xz

(ii) (-p + 2q + 3r)² = (-p)² + (2q)² + (3r)² + 2(-p) (2q) + 2(2q)(3r) + 2(3r) (- p)
= p²+ 4q² + 9r² – 4pq + 12qr – 6pr

(iii) (2p + 3) (2p – 4) (2p – 5)
[Here x = 2p, a = 3, b = -4 and c = -5]
= (2p)³ + (3 – 4 – 5) (2p)² + [(3)(-4) + (-4)(-5) + (3) (-5)] 2p + (3) (-4) (-5)
= 8p³ + (-6)(4p²) + (-12 + 20 – 15) 2p + 60
= 8p³ – 24p² – 14p + 60

(iv) (3a + 1) (3a – 2) (3a + 4)
[Here x = 3a, a = 1, b = -2 and c = 4]
= (3a)³ + (1 – 2 + 4) (3a)² + [(1)(-2) + (-2) (4) + (4) (1)] (3a) + (1) (-2) (4)
= 27a³ + 3(9a²) + (-2 – 8 + 4) (3a) – 8
= 27a³ + 27a² – 18a – 8

Question 2.
Using algebraic identity, find the coefficients of x², x and constant term without actual expansion.
(i) (x + 5)(x + 6)(x + 7)
Solution:
[Here x = x, a = 5, b = 6, c = 7]
(x + a) (x + b) (x + c) = x³ + (a + b + c)x² + (ab + bc + ac)x + abc
coefficient of x² = 5 + 6 + 7
= 18
coefficient of x = 30 + 42 + 35
= 107
constant term = (5) (6) (7)
= 210

(ii) (2x + 3)(2x – 5) (2x – 6)
Solution:
[Here x = 2x, a = 3, b = -5, c = -6]
(x + a) (x + b) (x + c) = x³ + (a + b + c)x² + (ab + bc + ac)x + abc
coefficient of x² = (3 – 5 – 6)4 [(2x)² = 4x²]
= (-8) (4)
= -32
coefficient of x = [(3)(-5) + (-5)(-6) + (-6)(3)](2)
= (-15 + 30-18) (2)
= (-3) (2)
= -6
constant term = (3) (-5) (-6)
= 90

Question 3.
If (x + a)(x + b)(x + c) = x³ + 14x² + 59x + 70, find the value of
(i) a + b + c
(ii) \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}\)
(iii) a² + b² + c²
(iv) \(\frac{a}{bc} + \frac{b}{ac} + \frac{c}{ab}\)
Solution:
(x + a) (x + b) (x + c) = x³ + 14x² + 59x + 70
x³ + (a + b + c)x² + (ab + bc + ac)x + abc = x³ + 14x² + 59x + 70
a + b + c = 14, ab + bc + ac = 59, abc = 70
(i) a + b + c = 14

(ii) \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}\) = \(\frac{bc+ac+ab}{abc}\)
= \(\frac{59}{70}\)

(iii) a² + b² + c² = (a + b + c)² – 2 (ab + bc + ac)
= (14)² – 2(59)
= 196 – 118
= 78

Question 4.
Expand:
(i) (3a – 4b)³
Solution:
(a – b)³ = a³ – b³ – 3ab (a – b)
(3a – 4b)³ = (3a)³ – (4b)³ – 3(3a)(4b)(3a – 4b)
= 27a³ – 64b³ – 36ab (3a – 4b)
= 27a³ – 64b³ – 108a²b + 144ab²

(ii) [x + \(\frac{1}{y}]^{3}\)
Solution:
(a + b)³ = a³ + b³ + 3ab (a + b)

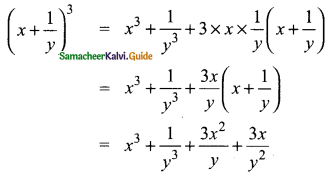
Question 5.
Evaluate the following by using identities:
(i) 98³
Solution:
98³ = (100 – 2)³ [(a – b)³ = a³ – b³ – 3ab (a – b)]
= 100³ – (2)³ – 3(100) (2) (100 – 2)
= 1000000 – 8 – 600(98)
= 1000000 – 8 – 58800
= 1000000 – 58808
= 941192

(ii) 1001³
Solution:
(1001)³ = (1000 + 1)³
[(a + b)³ = a³ + b³ + 3ab (a + b)]
= (1000)³ + 1³ + 3(1000) (1) (1000 + 1)
= 1000000000 + 1 + 3000 (1001)
= 1000000001 + 3003000
= 1003003001

Question 6.
If (x + y + z) = 9 and (xy + yz + zx) = 26, then find the value of x² + y² + z².
Solution:
x + y + z = 9; xy + yz + zx = 26
x² + y² + z² = (x + y + z)² – 2xy – 2yz – 2xz
= (x + y + z)² – 2 (xy + yz + zx)
= 9² – 2(26)
= 81 – 52
= 29

Question 7.
Find 27a³ + 64b³, If 3a + 4b = 10 and ab = 2
Solution:
3a + Ab = 10, ab = 2
27a³ + 64b³ = (3a)³ + (4b)³
[a³ + b³ = (a + b)³ – 3 ab (a + b)]
= (3a + 4b)³ – 3 × 3a × 4b (3a + 4b)
= 103 – 36ab (10)
= 1000 – 36(2)(10)
= 1000 – 720
= 280

Question 8.
Find x³ – y³, if x – y = 5 and xy = 14.
Solution:
x – y = 5, xy = 14
x³ – y³  = (x – y)³ + 3xy (x – y)
= 5³ + 3(14) (5)
= 125 + 210
= 335

Question 9.
If a + \(\frac{1}{a}\) = 6, then find the value of a³ +\(\frac{1}{a^3}\)
Solution:
a + \(\frac{1}{a}\) = 6 [a³ + b³ = (a + b)³ – 3ab (a + b)]

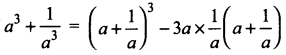
= 6³ – 3(6)
= 216 – 18
= 198

Question 10.
If x² + \(\frac{1}{x^2}\) = 23, then find the value of x + \(\frac{1}{x}\) and x³ + \(\frac{1}{x^3}\)
Solution:

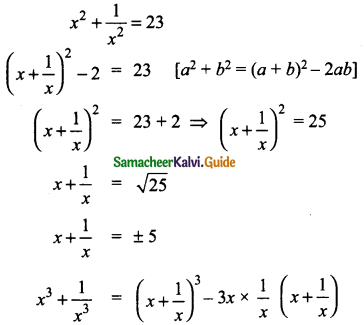
When x = 5 [a³ + b³ = (a + b)³ – 3ab (a + b)]
= (5)³ – 3(5)
= 125 – 15
= 110
when x = -5
x³ + \(\frac{1}{x^3}\) = (-5)³ – 3(-5)
= -125 + 15
= -110
∴ x³ + \(\frac{1}{x^3}\) = ±110

Question 11.
If (y – \(\frac{1}{y})^{3}\) = 27 then find the value of y³ – \(\frac{1}{y^3}\)
Solution:

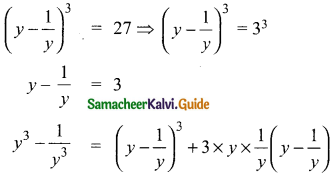
= 3³ + 3(3)
= 27 + 9
= 36

Question 12.
Simplify:
(i) (2a + 3b + 4c) (4a² + 9b² + 16c² – 6ab – 12bc – 8ca)
(ii) (x – 2y + 3z) (x² + 4y² + 9z² + 2xy + 6yz – 3xz)
Solution:
x³ + y³ + z³ – 3xyz ≡ (x + y + z) (x² + y² + z² – xy – yz – zx)
(i) (2a + 3b + 4c) (4a² + 9b² + 16c² – 6ab – 12bc – 8ea)
= (2a)³ + (3b)³ + (4c)³ – 3 (2a) (3b) (4c)
= 8a³ + 27b³ + 64c³ – 72abc

(ii) (x – 2y + 3z) (x² + 4y² + 9z² + 2xy + 6yz – 3xz)
= x³ + (-2y)³ + (3z)³ – 3(x) (-2y) (3z)
= x³ – 8y³ + 27z³ + 18xyz

Question 13.
By using identity evaluate the following:
(i) 7³ – 10³ + 3³
Solution:
x³ + y³ + z³ – 3xyz = (x + y + z) (x² + y² + z² – xy – yz – zx)
We know that a + b + c = 0 then a³ + b³ + c³ = 3ab
a + b + c = 7 + (-10) + 3
= 10 – 10
= 0
∴ 7³ – 10³ + 3³ = 3(7) (-10) (3)
= -630

(ii) 1 + \(\frac{1}{8}\) – \(\frac{27}{8}\)
Solution:
We know that a³ + b³ + c³ = 0 then a + b + c = 3abc

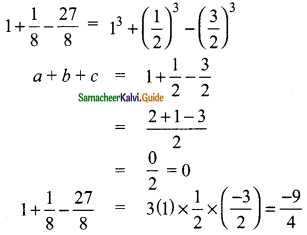
Question 14.
If 2x -3y – 4z = 0, then find 8x³ – 27y³ – 64z³.
Solution:
We know x³ +y³ + z³ – 3xyz = (x + y + z) (x² + y² + z² – xy – yz – zx)
x³ + y³ + z³ = (x + y + z) (x² +y² + z² – xy – yz – zx) + 3xyz
8x³ – 27y³ – 64z³ = (2x)³ + (-3y)³ + (-4z)³
= (2x – 3y- 4z) [(2x)² + (-3y)² + (-4z)² – (2x)(-3y) – (-3y) (-4z) -(-4z)(2x)] + 3(2x)(-3y)(-4z)
= 0 (4x² + 9y² + 16z² + 6xy – 12yz + 8xz) + 72xyz
= 72xyz
8x³ – 27y³ – 64z³ = 72xyz

Students can download Maths Chapter 1 Set Language Ex 1.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.2

Question 1.
Find the cardinal number of the following sets.
(i) M = {p, q, r, s, t, u}
(ii) P = {x : x = 3n + 2, n ∈ W and x < 15}
(iii) Q = {y : y = \(\frac{4}{3n}\), n ∈ N and 2 < n ≤ 5}
(iv) R = {x : x is an integer, x ∈ Z and – 5 ≤ x < 5}
(v) S = The set of all leap years between 1882 and 1906.
Solution:
(i) n (M) = 6
(ii) n (P) = 5 [n = {0, 1, 2, 3 . . . . 14}]
(iii) Since n = {3, 4, 5} ; n (Q) = 3
(iv) X = {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4} ∴ n (R) = 10
(v) S = {1884, 1888, 1892, 1896, 1904}; n (S) = 5

Question 2.
Identify the following sets as finite or infinite.
(i) X = The set of all districts in Tamilnadu.
(ii) Y = The set of all straight lines passing through a point.
(iii) A = {x : x ∈ Z and x < 5}
(iv) B = {x : x² – 5x + 6 = 0, x ∈ N}
Solution:
(i) Finite
(ii) Infinite set (many lines can be drawn from a point)
(iii) Infinite set {A = ……. -2, -1, 0, 1, 2, 3, 4}
(iv) Finite set [x² – 5x + 6 = 0 ⇒ (x – 3) (x – 2) = 0; x = 3 and 2]

Question 3.
Which of the following sets are equivalent or unequal or equal sets?
(i) A = The set of vowels in the English alphabets.
B = The set of all letters in the word “VOWEL”
(ii) C = {2, 3, 4, 5}
D = {x : x ∈ W, 1 < x < 5}
(iii) X = {x : x is a letter in the word “LIFE”}
Y = {F, I, L, E}
(iv) G = {x : x is a prime number and 3 < x < 23}
H = {x : x is a divisor of 18}
Solution:
(i) Equivalent set [n(A) = n(B) = 5] ∴ A ≈ B
(ii) Unequal sets [C = {2, 3, 4, 5}; D = {2, 3, 4}]
(iii) Equal sets [X = {L, I, F, E}; Y = {F, I, L, E} [n(X) = 4 = n(Y)] ∴ X ≈ Y
(iv) Equivalent sets [G = {5, 7, 11, 13, 17, 19}; H = {1, 2, 3, 6, 9, 18}]
[n(G) = n(H) = 6 ∴ G ≈ H)]

Question 4.
Identify the following sets as null set or singleton set.
(i) A = {x : x ∈ N, 1 < x < 2}
(ii) B = The set of all even natural numbers which are not divisible by 2
(iii) C = {0}.
(iv) D = The set of all triangles having four sides.
Solution:
(i) Null set [No natural numbers is in between 1 and 2]
(ii) Null set [All the even natural numbers are not divisible by 2]
(Hi) Singleton set [n (C) = 1]
(iv) Null set [All the triangles has 3 sides]

Question 5.
State which pairs of sets are disjoint or overlapping?
(i) A = {f, i, a, s} and B = {a, n, f, h, s}
A = {f, i, a, s} and B = {a, n, f, h, s}
A and B are overlapping sets

(ii) C = {x : x is a prime number, x > 2} and D = {x : x is an even prime number}
C= {3, 5, 7…….}
D = {2}
C and D are disjoint sets

(iii) E = {x : x is a factor of 24} and F = {x : x is a multiple of 3, x < 30}
E = {1, 2, 3, 4, 6, 8, 12, 24}
F = {3, 6, 9, 12, 15, 18, 21, 24, 27} [Hint: E ∩ F = {3, 6, 24, …….}]
E and F are overlapping sets

Question 6.
If S = {square, rectangle, circle, rhombus, triangle}. List the elements of the following subset of S.
(i) The set of shapes which have 4 equal sides.
(ii) The set of shapes which have radius.
(iii) The set of shapes in which the sum of all interior angles is 180°.
(iv) The set of shapes which have 5 sides.
Solution:
(i) Subset of S = {square, rhombus}
(ii) Subset of S = {circle}
(iii) Subset of S = {triangle}
(iv) Subset of S = { }

Question 7.
If A = {a,{a, b}}, write all the subsets of A.
Solution:
A = {a, {a, b}}
Subset of A are Ø, {a}, {a, b}, {a, {a, b}} (or) { }, {a}, {a,b, {a,{a,b}}
P(A) = {Ø, {a}, {a, b}, {a {a, b}} (or) {{ }, {a}, {a,b, {a,{a,b}}

Question 8.
Write down the power set of the following sets.
(i) A = {a, b}
(ii) B = {1, 2, 3}
(iii) D = {p, q, r, s}
(iv) E = Ø
Solution:
(i) A = {a, b)
P(A) = {{},{a},{b}, {a, b}}

(ii) B = {1, 2, 3}
P(B) = {{}, {1}, {2}, {3}, {1,2}, {2, 3}, {1,3}, {1,2,3}}

(iii) D = {p, q, r, s}
P(D) = {{},{p},{q},{r},{s},{p, q} {p, r} {p, s}
{q, r}, {q, s}, {r, s}, {p, q, r} {q, r, s}
{p, r, s} {p, q, s} {p, q, r, s}}

(iv) E = Ø
P(E) = {{}}
Note: (empty set is the subset of all the sets)

Question 9.
Find the number of subsets and the number of proper subsets of the following sets.
(i) W = {red, blue, yellow}
(ii) X = {x² : x ∈ N, x² ≤ 100}
Solution:
(i) W = {red, blue, yellow}
n (W) = 3
The number of subsets of W = n [P(W)] = 2^m
= 2³ = 8
Number of proper subsets of W = n[P(W)] – 1
= 8 – 1
= 7 (or)
Number of proper subsets of W = 2^m – 1
= 2³ – 1 = 8 – 1 = 7

(ii) X = {x² : x ∈ N, x² ≤ 100}.
X= {1,2, 3, 4, …. 10}
n(X) = 10
The number of subsets of X = n[P(X)]
= 2^m
= 2¹⁰ = 1024
Number of proper subsets of X = 2^m – 1
= 1024 – 1
= 1023

Question 10.
(i) If n(A) = 4, find n[P(A)]
(ii) If n(A) = 0, find n[P(A)]
(Hi) If n[P(A)] = 256, find n(A)
Solution:
(i) n (A) = 4
n [P(A)] = 2^m = 2⁴
= 16

(ii) n (A) = 0
n [P(A)] = 2^m = 2° = 1

(iii) n [P(A)] = 256

2^m = 2⁸
∴ n (A) = 8

శ్రీ సాయి దీక్షా విధానము

Students can download Maths Chapter 1 Set Language Ex 1.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.1

Question 1.
Which of the following are sets?
(i) The collection of prime numbers upto 100
(ii) The collection of rich people in India
(iii) The collection of all rivers in India
(iv) The collection of good hockey players
Solution:
(i) It is a set
(ii) It is not a set (The word “rich” is not well defined)
(iii) It is a set
(iv) It is not a set (The word “good” is not well defined)

Question 2.
List the set of letters of the following words in Roster form.
(i) INDIA
(ii) PARALLELOGRAM
(iii) MISSISSIPPI
(iv) CZECHOSLOVAKIA
Solution:
(i) A = {I, N, D, A}
(ii) B = {P, A, R, L , E, O, G, M}
(iii) C = {M, I, S, P}
(iv) D = {C, Z, E, H, O, S, L, V, A, K, I}

Question 3.
Consider the following sets A = {0, 3, 5, 8}, B = {2, 4, 6, 10} and C = {12, 14, 18, 20}.
(a) State whether True or False:
(i) 18 ∈ C
(if) 6 ∉ A
(iii) 14 ∉ C
(iv) 10 ∈ B
(v) 5 ∈ B
(vi) 0 ∈ B
Solution:
(i) True
(ii) True
(iii) False
(iv) True
(v) False
(vi) False

(b) Fill in the blanks:
(i) 3 ∈ …………
(ii) 14 ∈…………
(iii) 18 ……….. B
(iv) 4 ………. B
Solution:
(i) A
(ii) C
(iii) ∉
(iv) ∈

Question 4.
Represent the following sets in Roster form.
(i) A = The set of all even natural numbers less than 20.
(ii) B = {y : y = \(\frac{1}{2n}\), n∈N, n ≤ 5}
(iii) C = {x : x is perfect cube, 27 < x < 216}
(iv) D = {x : x ∈Z, – 5 < x ≤ 2}
Solution:
(i) A= {2, 4, 6, 8, 10, 12, 14, 16, 18}
(ii) B = {\(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{6}\), \(\frac{1}{8}\), \(\frac{1}{10}\)}
(iii) C = {64, 125}
(iv) D = {-4, -3, -2, -1, 0, 1, 2}

Question 5.
Represent the following sets in set builder form.
(i) B = The set of all cricket players in India who scored double centuries in one day internationals.
(ii) C = {\(\frac{1}{2}\), \(\frac{2}{3}\), \(\frac{3}{4}\), …….}
(iii) D = The set of all Tamil months in a year.
(iv) E = The set of odd Whole numbers less than 9.
Solution:
(i) B = {x : x is a set of all cricket players in India who scored double centuries in one day internationals}
(ii) C = {x : n ∈ N, x = \(\frac{n}{n + 1}\) }
(iii) D = {x : x ∈ set of all Tamil months in a year}
(iv) E = {x : x is an odd whole number and x < 9}

Question 6.
Represent the following sets in descriptive form.
(i) P = { January, June, July}
(ii) Q = {7, 11, 13, 17, 19, 23, 29}
(iii) R = {x : x∈N, x < 5}
(iv) S = {x : x is a consonant in English alphabets}
Solution:
(i) P = The set of all months beginning with the letter “J”
(ii) Q = The set of all prime numbers between 5 and 31
(iii) R = The set of natural numbers less than 5
(iv) S = The set of consonants in English alphabets

Read More:

ముకుందమాలా

Students can download Maths Chapter 8 Statistics Ex 8.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 8 Statistics Ex 8.1

Question 1.
In a week, temperature of a certain place is measured during winter are as follows 26°C, 24°C, 28°C, 31°C, 30°C, 26°C, 24°C. Find the mean temperature of the week.
Solution:
Mean temperature of the week

= 27°C
Mean temperature of the week 27° C

Question 2.
The mean weight of 4 members of a family is 60 kg. Three of them have the weight 56 kg, 68 kg and 72 kg respectively. Find the weight of the fourth member.
Solution:
Weight of 4 members = 4 × 60 kg
= 240 kg
Weight of three members = 56 kg + 68 kg + 72 kg
= 196 kg
Weight of the fourth member = 240 kg – 196 kg
= 44 kg

Question 3.
In a class test in mathematics, 10 students scored 75 marks, 12 students scored 60 marks, 8 students scored 40 marks and 3 students scored 30 marks. Find the mean of their score.
Solution:
Total marks of 10 students = 10 × 75 = 750
Total marks of 12 students = 12 × 60 = 720
Total marks of 8 students = 8 × 40 = 320
Total marks of 3 students = 3 × 30 = 90
Total marks of (10 + 12 + 8 + 3) 33 students
= 750 + 720 + 320 + 90
= 1880
Mean of marks = \(\frac{1880}{33}\)
= 56.97 (or) 57 approximately
Aliter:
Total number of students = 10+12 + 8 + 3
= 33
Mean of their marks

= 56.97 (or) 57 approximately

Question 4.
In a research laboratory scientists treated 6 mice with lung cancer using natural medicine. Ten days later, they measured the volume of the tumor in each mouse and given the results in the table.

find the mean.
Solution:

\(\bar { x }\) = \(\frac{Σfx}{Σf}\)
= \(\frac{2966}{21}\)
= 141.238
= 141.24
The Arithmetic mean = 141.24 mm³

Question 5.
If the mean of the following data is 20.2, then find the value of p.

Solution:

\(\bar { x }\) = \(\frac{Σfx}{Σf}\)
20.2 = \(\frac{610+20p}{30+p}\)
610 + 20 p = 20.2 (30 + p)
610 + 20 p = 606 + 20.2 p
610 – 606 = 20.2 p – 20 p
4 = 0.2 p
p = \(\frac{4}{0.2}\)
= \(\frac{4×10}{2}\)
= 20
The value of p = 20

Question 6.
In the class, weight of students is measured for the class records. Calculate mean weight of the class students using direct method.

Solution:

Arithmetic mean \(\bar { x }\) = \(\frac{Σfx}{Σf}\)
= \(\frac{2010}{50}\)
= 40.2
Arithmetic mean = 40.2

Question 7.
Calculate the mean of the following distribution using Assumed Mean Method.

Solution:
Assumed Mean (A) = 25

Arithmetic mean (\(\bar { x }\)) = A+\(\frac{Σfd}{Σf}\)
= 25 + \(\frac{270}{63}\)
= 25 + 4. 29
Assumed Mean = 29.29

Question 8.
Find the Arithmetic Mean of the following data using Step Deviation Method:

Solution:
Assumed Mean (A) = 32

Arithmetic mean = A+\(\frac{Σfd}{Σf}\) × c
= 32 + (\(\frac{-77.5}{105}\)×4)
= 32 – 2.95
= 29.05
Arithmetic mean = 29.05

Students can download Maths Chapter 7 Mensuration Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 7 Mensuration Additional Questions

I. Choose the Correct Answer

Question 1.
If the sides of a triangles are 5 cm, 6 cm and 7 cm then the area is ……..
(a) 18 cm²
(b) 6 √2 cm²
(c) 6 √6 cm²
(d) 6 √3 cm²
Solution:
(c) 6 √6 cm²

Question 2.
The perimeter of an equilateral triangle is 60 cm then the area is ………
(a) 60 √3 cm²
(b) 20 √3 cm²
(c) 50 √3 cm²
(d) 100 √3 cm²
Solution:
(d) 100 √3 cm²

Question 3.
The total surface area of the cuboid with dimension 20 cm × 30 cm × 15 cm is ………
(a) 2700 cm²
(b) 1500 cm²
(c) 2500 cm²
(d) 3000 cm²
Solution:
(a) 2700 cm²

Question 4.
The number of bricks each measuring 70 cm × 80 cm × 40 cm that will be required to build a wall whose dimensions are 7 m × 8 m × 4 m is ……..
(a) 4000
(b) 3000
(c) 2000
(d) 1000
Solution:
(d) 1000

Question 5.
The volume of a cube is 4913 m² then the length of its side is ……..
(a) 13 m
(b) 17 m
(c) 34 m
(d) 27 m
Solution:
(b) 17 m

II. Answer the Following Questions

Question 6.
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non parallel sides are 14 m and 13 m. Find the area of the field.
Solution:
The non parallel sides are 13 m and 14 m. Draw BE || AD. Such that BE = 13 m
∴ ABED is a parallelogram

To find Area of a ΔBCE
a = 13 m, b = 15 m and c = 14 m
s = \(\frac{a+b+c}{2}\)
= \(\frac{13+15+14}{2}\)
= \(\frac{42}{2}\)
= 21 m
s – a = 21 – 13 = 8 m
s – b = 21 – 15 = 6 m
s – c = 21 – 14 = 7 m
Area of a ΔBCE

= 2² × 3 × 7
= 84 m²
Let the height of the triangle BF be x
Area of the ΔBEC = 84 m²
= \(\frac{1}{2}\) × b × h = 84
= \(\frac{1}{2}\) × 15 × h = 84
x = \(\frac{84×2}{15}\)
= \(\frac{56}{5}\) m
= 11.2 m
Area of parallelogram ABED = base × height sq. units
= 10 × 11.2 m²
= 112 m²
∴ Area of the field = Area of ΔBCE + Area of parallelogram ABED
= 84 m² + 112 m²
= 196 m²
(OR)
Area of the field = Area of the trapezium ABCD
= \(\frac{1}{2}\) h (a + b)
= \(\frac{1}{2}\) × 11.2 (25 + 10)
= \(\frac{1}{2}\) × 11.2 (35)
= 196 m²

Question 7.
Find the area of a quadrilateral ABCD in which AB = 8 cm, BC = 6 cm, CD = 8 cm, DA = 10 cm and AC = 10 cm and ⌊B = 90°.
Solution:

In ΔABC, ⌊B = 90°
∴ ABC is a right angle triangle
Area of the right ΔABC = \(\frac{1}{2}\) × AB × BC sq.units
= \(\frac{1}{2}\) × 8 × 6 cm²
= 24 cm²
In ΔACD a = 10 cm, b = 8 cm and c = 10 cm
s = \(\frac{a+b+c}{2}\)
= \(\frac{10+8+10}{2}\)
= \(\frac{28}{2}\)
= 14 cm
s – a = 14 – 10 = 4 cm
s – b = 14 – 8 = 6 cm
s – c = 14 – 10 = 4 cm
Area of ΔACD = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{14×4×6×4}\)
= \(\sqrt{2×7×4×2×3×4}\)
= 4 × 2 \(\sqrt{21}\) cm²
= 8\(\sqrt{21}\) cm²
= 8 × 4.58
= 36.64 cm²
Area of the quadrilateral ABCD
= Area of ΔABC + Area of ΔACD
= 24 cm² + 36.64 cm²
= 60.64 cm²
Area of the quadrilateral = 60.64 cm²

Question 8.
The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of Rs 7.50 per m².
Solution:
Length of the room (l) = 5 m
Breadth of the room (b) = 4 m
Height of the room (h) = 3 m
Area for white washing = Lateral surface area of four walls + Area of the ceiling
= 2(l + b) × h + (l × b)
= 2(5 + 4) × 3 + (5 × 4) m²
= (2 × 9 × 3 + 20) m²
= (54 + 20) m²
= 74 m²
Cost of white washing for one m² = Rs 7.50
Cost of white washing for 74 m² = Rs 74 × 7.50
= Rs 555
The required cost = Rs 555

Question 9.
How many hollow blocks of size 30 cm × 15 cm × 20 cm are needed to construct a wall 60 m in length 0.3 m in breadth and 2 m in height.
Solution:
Length of a wall = 60 m = 6000 cm
Breadth of a wall = 0.3 m = 30 cm
Height of a wall = 2 m = 200 cm
Volume of the wall = l × b × h sq. unit
= 6000 × 30 × 200 cm³
For hollow block
l = 30 cm, b = 15 cm, h = 20 cm
Volume of one hollow block = l × b × h
= 30 × 15 × 20 cm²
Number of hollow blocks required

= 4000
∴ Number of bricks = 4000

Question 10.
Find the number of cubes of side 3 cm that can be cut from a cuboid of dimensions 10 cm × 9 cm × 6 cm.
Solution:
Side of a cube = 3 cm
Volume of a cube = a³ cm
= 3 × 3 × 3 cm³
Length of the cuboid (l) = 10 cm
Breadth of the cuboid (b) = 9 cm
Height of the cuboid (h) = 6 cm
Volume of the cuboid = l × b × h cu. unit
= 10 × 9 × 6 cm
Number of cubes

∴ Number of cubes = 20

Students can download Maths Chapter 6 Trigonometry Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Additional Questions

I. Choose the Correct Answer

Question 1.
The value of cosec² 60 – 1 is equal to ……..
(a) cos² 60
(b) cot² 60
(c) sec² 60
(d) tan² 60
Solution:
(b) cot² 60

Question 2.
The value of cos 60° cos 30° – sin 60° sin 30° is equal is ……..
(a) cosec 90°
(b) tan 90°
(c) sin 30° + cos 30°
(d) cos 90°
Solution:
(d) cos 90°

Question 3.
The value of \(\frac{sin 57°}{cos 33°}\) is …….
(a) cot 63°
(b) tan 27°
(c) 1
(d) 0
Solution:
(c) 1

Question 4.
If 3 cosec 36° = sec 54° then the value of x is ……..
(a) 0
(b) 1
(c) \(\frac{1}{3}\)
(d) \(\frac{3}{4}\)
Solution:
(c) \(\frac{1}{3}\)

Question 5.
If cos A cos 30° = \(\frac{√3}{4}\), then the measures of A is ……..
(a) 90°
(b) 60°
(c) 45°
(d) 30°
Solution:
(b) 60°

II. Answer the Following Question

Question 1.
Given Sec θ = \(\frac{13}{12}\). Calculate all other trigonometric ratios.
Solution:
In the right triangle ABC

BC² = AC² – AB²
= 13² – 12²
= 169 – 144
= 25
∴ BC = \(\sqrt{25}\)
= 5

Question 2.
If 3 cot A = 4 check weather \(\frac{1- tan²A}{1+ tan²A}\) = cos² A – sin² A or not?
Solution:
3 cot A = 4
cot A = \(\frac{4}{3}\)
In the right ΔABC

AC² = AB² + BC²
= 4² + 3²
= 16 + 9
= 25
= \(\sqrt{25}\)
= 5

Hence \(\frac{1- tan²A}{1+ tan²A}\) = cos² A – sin² A
R.H.S = cos² A – sin² A

L.H.S = R.H.S

Question 3.
Evaluate \(\frac{sin 30° + tan 45° – cosec 60°}{sec 30° + cos 60° + cot 45°}\)
Solution:
sin 30° = \(\frac{1}{2}\); tan 45° = 1; cosec 60° = \(\frac{2}{√3}\); sec 30° = \(\frac{2}{√3}\); cos 60° = \(\frac{1}{2}\); cot 45° = 1
\(\frac{sin 30° + tan 45° – cosec 60°}{sec 30° + cos 60° + cot 45°}\)

The value is \(\frac{43-24√3}{11}\)

Question 4.
Find A if sin 20° tan A sec 70° = √3
Solution:
sin 20° . tan A . sec 70° = √3
sin 20° . sec 70° . tan A = √3
sin (90° – 70°). sec 70° . tan A = √3
cos 70° × latex]\frac{1}{cos 70°}[/latex] tan A = √3
tan A = √3
tan A = tan 60°
∴ ∠A = 60°

Question 5.
Find the area of the right triangle with hypotenuse 8 cm and one of the acute angles is 57°
Solution:
In the ΔABC

sin C = \(\frac{AB}{AC}\)
Sin 57° = \(\frac{AB}{8}\)
0.8387 = \(\frac{AB}{8}\)
∴ AB = 0.8387 × 8
= 0.71 cm
In the ΔABC
cos C = \(\frac{BC}{AC}\)
cos 57° = \(\frac{BC}{8}\)
0.5446 = \(\frac{BC}{8}\)
BC = 0.5446 × 8
= 4.36
Area of the right ΔABC
= \(\frac{1}{2}\) × AB × BC sq. units
= \(\frac{1}{2}\) × 6.71 × 4.36 cm²
= 14.62 cm²
Area of the Δ = 14.62 cm²