Students can download Maths Chapter 7 Mensuration Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 7 Mensuration Additional Questions
I. Choose the Correct Answer
Question 1.
If the sides of a triangles are 5 cm, 6 cm and 7 cm then the area is ……..
(a) 18 cm²
(b) 6 √2 cm²
(c) 6 √6 cm²
(d) 6 √3 cm²
Solution:
(c) 6 √6 cm²
Question 2.
The perimeter of an equilateral triangle is 60 cm then the area is ………
(a) 60 √3 cm²
(b) 20 √3 cm²
(c) 50 √3 cm²
(d) 100 √3 cm²
Solution:
(d) 100 √3 cm²
![]()
Question 3.
The total surface area of the cuboid with dimension 20 cm × 30 cm × 15 cm is ………
(a) 2700 cm²
(b) 1500 cm²
(c) 2500 cm²
(d) 3000 cm²
Solution:
(a) 2700 cm²
Question 4.
The number of bricks each measuring 70 cm × 80 cm × 40 cm that will be required to build a wall whose dimensions are 7 m × 8 m × 4 m is ……..
(a) 4000
(b) 3000
(c) 2000
(d) 1000
Solution:
(d) 1000
Question 5.
The volume of a cube is 4913 m² then the length of its side is ……..
(a) 13 m
(b) 17 m
(c) 34 m
(d) 27 m
Solution:
(b) 17 m
![]()
II. Answer the Following Questions
Question 6.
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non parallel sides are 14 m and 13 m. Find the area of the field.
Solution:
The non parallel sides are 13 m and 14 m. Draw BE || AD. Such that BE = 13 m
∴ ABED is a parallelogram
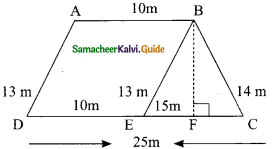
To find Area of a ΔBCE
a = 13 m, b = 15 m and c = 14 m
s = \(\frac{a+b+c}{2}\)
= \(\frac{13+15+14}{2}\)
= \(\frac{42}{2}\)
= 21 m
s – a = 21 – 13 = 8 m
s – b = 21 – 15 = 6 m
s – c = 21 – 14 = 7 m
Area of a ΔBCE
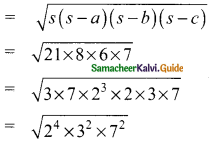
= 2² × 3 × 7
= 84 m²
Let the height of the triangle BF be x
Area of the ΔBEC = 84 m²
= \(\frac{1}{2}\) × b × h = 84
= \(\frac{1}{2}\) × 15 × h = 84
x = \(\frac{84×2}{15}\)
= \(\frac{56}{5}\) m
= 11.2 m
Area of parallelogram ABED = base × height sq. units
= 10 × 11.2 m²
= 112 m²
∴ Area of the field = Area of ΔBCE + Area of parallelogram ABED
= 84 m² + 112 m²
= 196 m²
(OR)
Area of the field = Area of the trapezium ABCD
= \(\frac{1}{2}\) h (a + b)
= \(\frac{1}{2}\) × 11.2 (25 + 10)
= \(\frac{1}{2}\) × 11.2 (35)
= 196 m²
![]()
Question 7.
Find the area of a quadrilateral ABCD in which AB = 8 cm, BC = 6 cm, CD = 8 cm, DA = 10 cm and AC = 10 cm and ⌊B = 90°.
Solution:
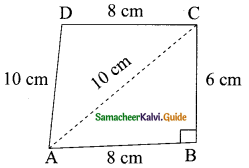
In ΔABC, ⌊B = 90°
∴ ABC is a right angle triangle
Area of the right ΔABC = \(\frac{1}{2}\) × AB × BC sq.units
= \(\frac{1}{2}\) × 8 × 6 cm²
= 24 cm²
In ΔACD a = 10 cm, b = 8 cm and c = 10 cm
s = \(\frac{a+b+c}{2}\)
= \(\frac{10+8+10}{2}\)
= \(\frac{28}{2}\)
= 14 cm
s – a = 14 – 10 = 4 cm
s – b = 14 – 8 = 6 cm
s – c = 14 – 10 = 4 cm
Area of ΔACD = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{14×4×6×4}\)
= \(\sqrt{2×7×4×2×3×4}\)
= 4 × 2 \(\sqrt{21}\) cm²
= 8\(\sqrt{21}\) cm²
= 8 × 4.58
= 36.64 cm²
Area of the quadrilateral ABCD
= Area of ΔABC + Area of ΔACD
= 24 cm² + 36.64 cm²
= 60.64 cm²
Area of the quadrilateral = 60.64 cm²
![]()
Question 8.
The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of Rs 7.50 per m².
Solution:
Length of the room (l) = 5 m
Breadth of the room (b) = 4 m
Height of the room (h) = 3 m
Area for white washing = Lateral surface area of four walls + Area of the ceiling
= 2(l + b) × h + (l × b)
= 2(5 + 4) × 3 + (5 × 4) m²
= (2 × 9 × 3 + 20) m²
= (54 + 20) m²
= 74 m²
Cost of white washing for one m² = Rs 7.50
Cost of white washing for 74 m² = Rs 74 × 7.50
= Rs 555
The required cost = Rs 555
![]()
Question 9.
How many hollow blocks of size 30 cm × 15 cm × 20 cm are needed to construct a wall 60 m in length 0.3 m in breadth and 2 m in height.
Solution:
Length of a wall = 60 m = 6000 cm
Breadth of a wall = 0.3 m = 30 cm
Height of a wall = 2 m = 200 cm
Volume of the wall = l × b × h sq. unit
= 6000 × 30 × 200 cm³
For hollow block
l = 30 cm, b = 15 cm, h = 20 cm
Volume of one hollow block = l × b × h
= 30 × 15 × 20 cm²
Number of hollow blocks required
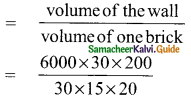
= 4000
∴ Number of bricks = 4000
![]()
Question 10.
Find the number of cubes of side 3 cm that can be cut from a cuboid of dimensions 10 cm × 9 cm × 6 cm.
Solution:
Side of a cube = 3 cm
Volume of a cube = a³ cm
= 3 × 3 × 3 cm³
Length of the cuboid (l) = 10 cm
Breadth of the cuboid (b) = 9 cm
Height of the cuboid (h) = 6 cm
Volume of the cuboid = l × b × h cu. unit
= 10 × 9 × 6 cm
Number of cubes
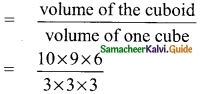
∴ Number of cubes = 20