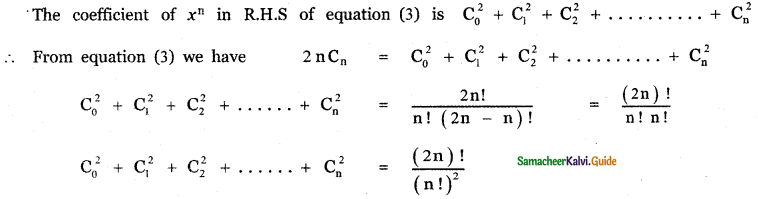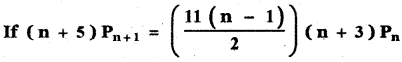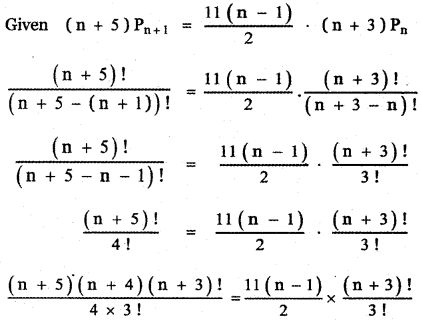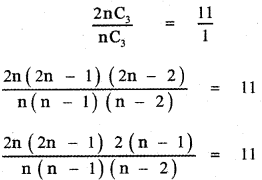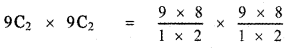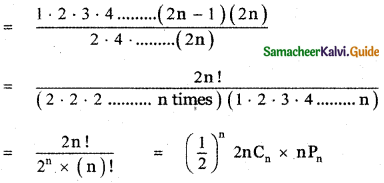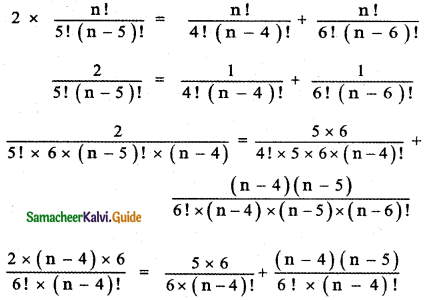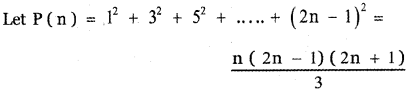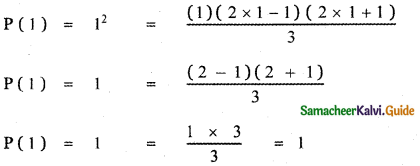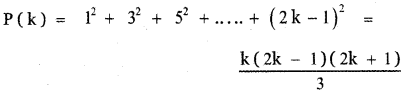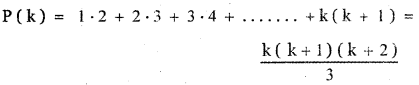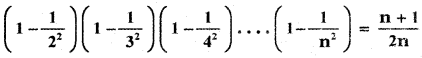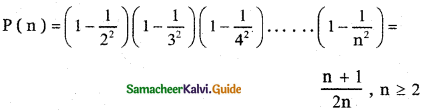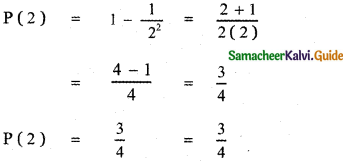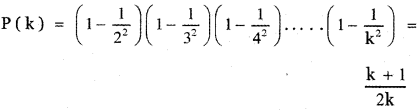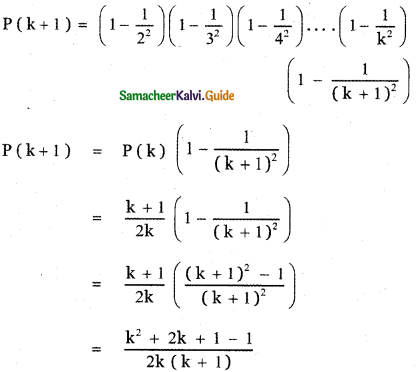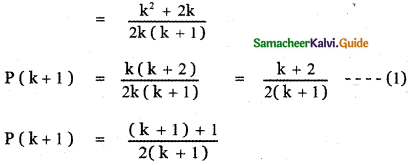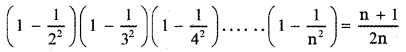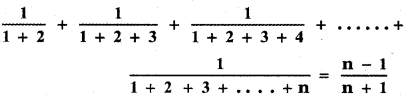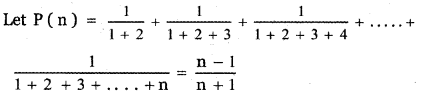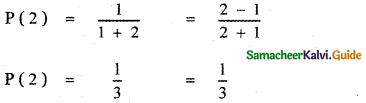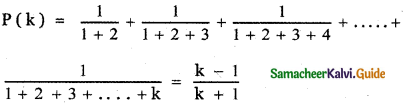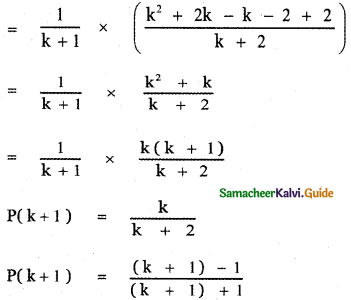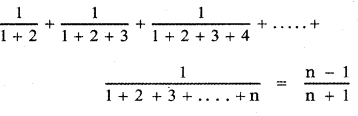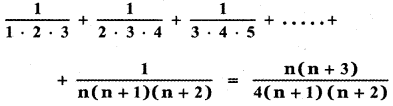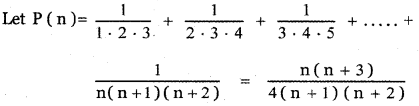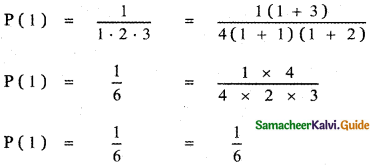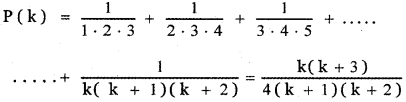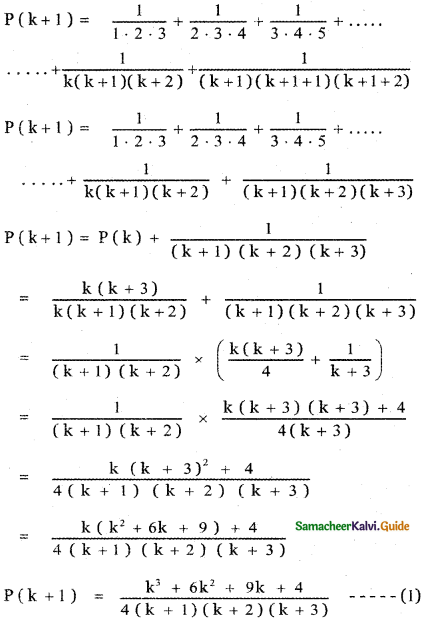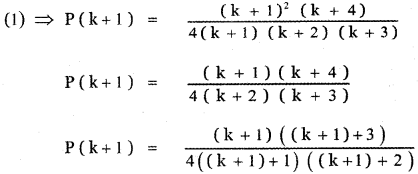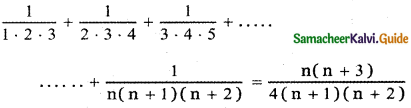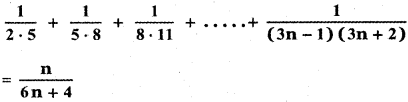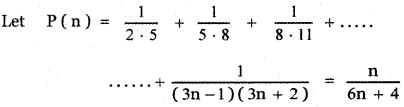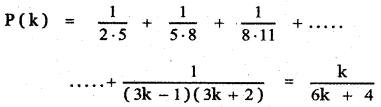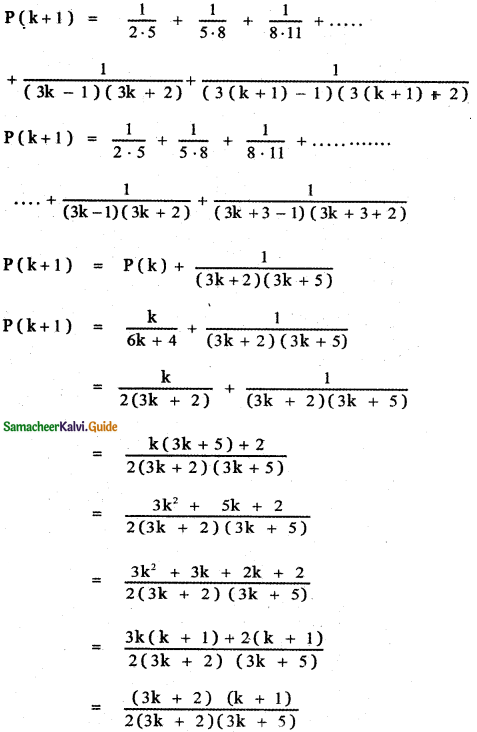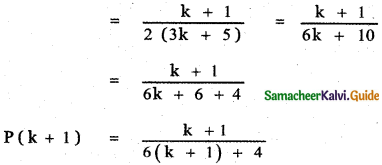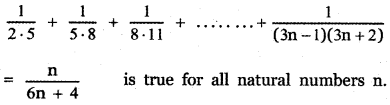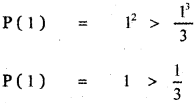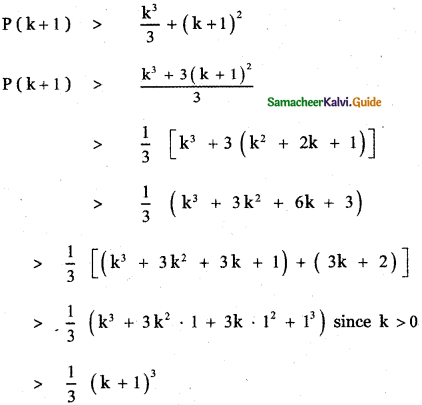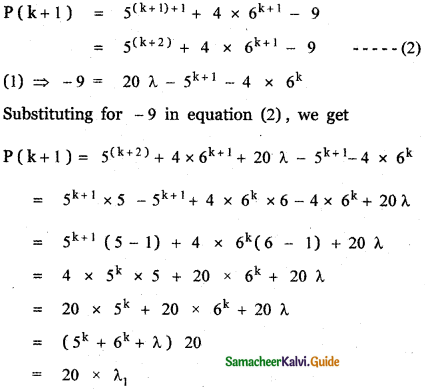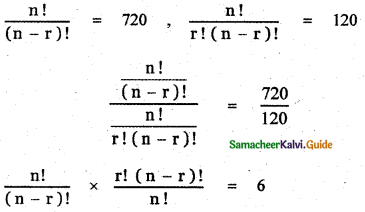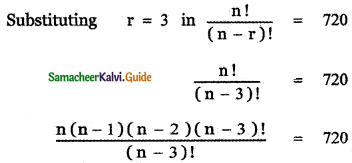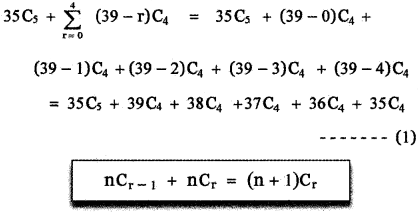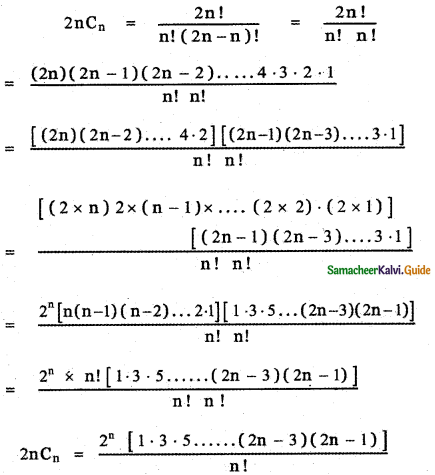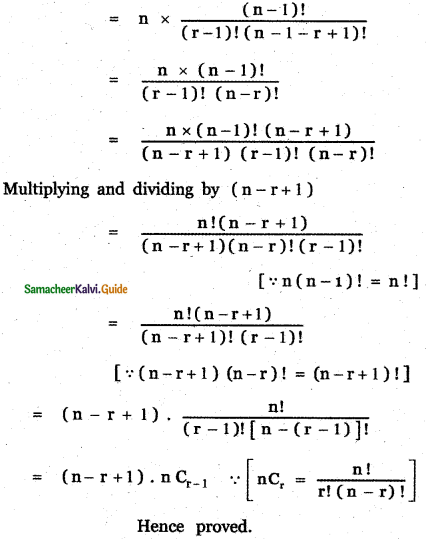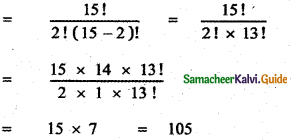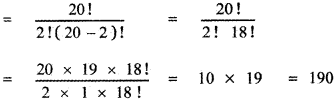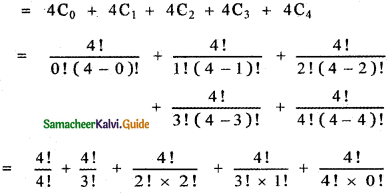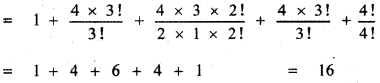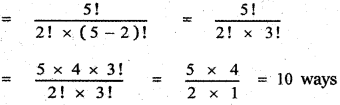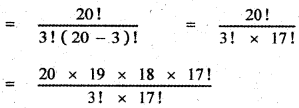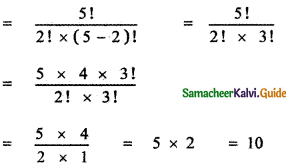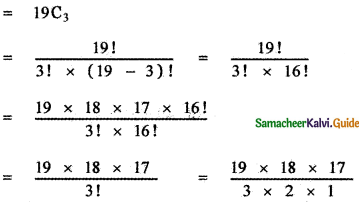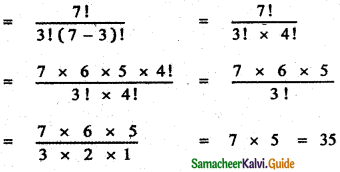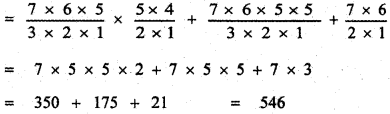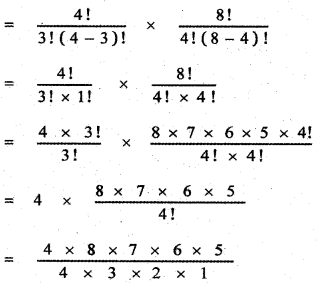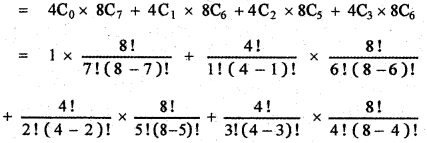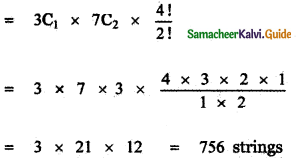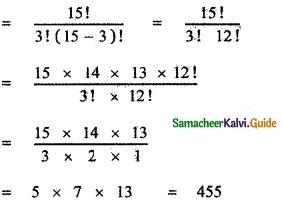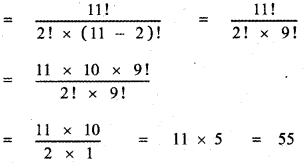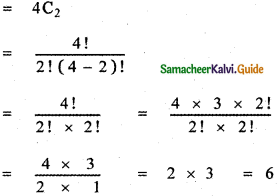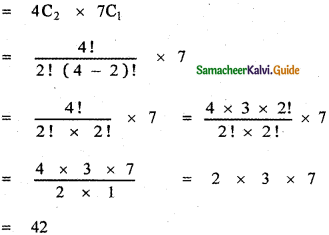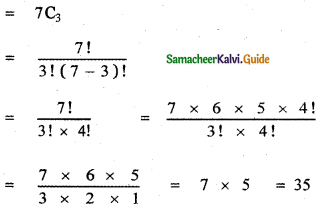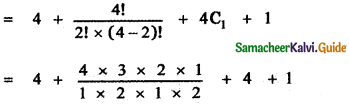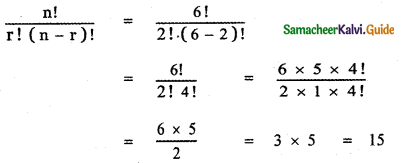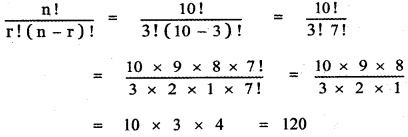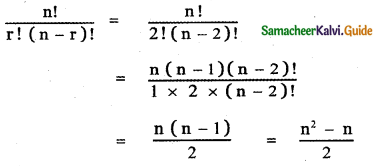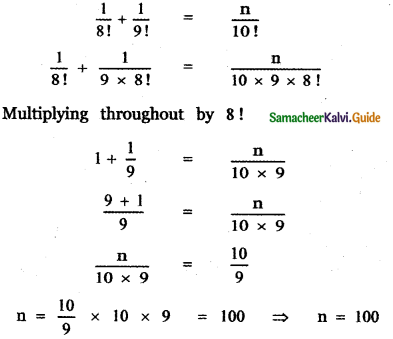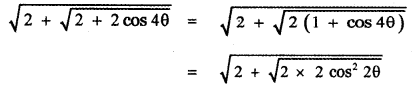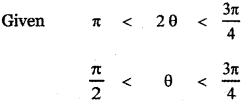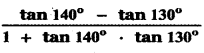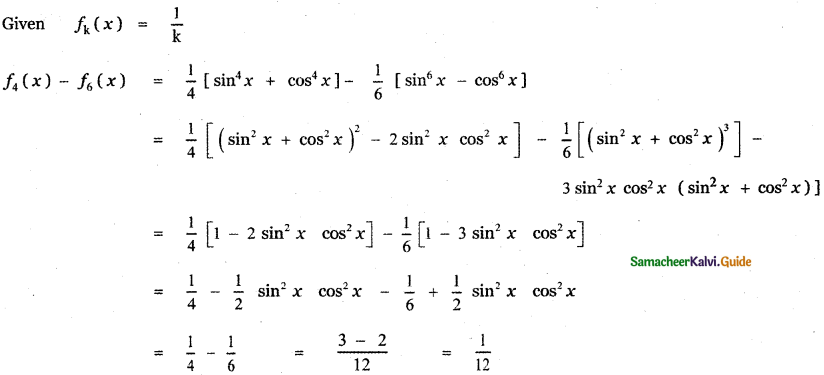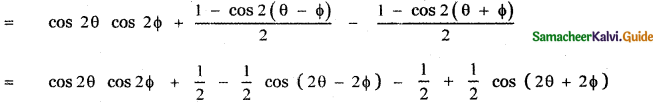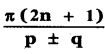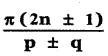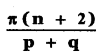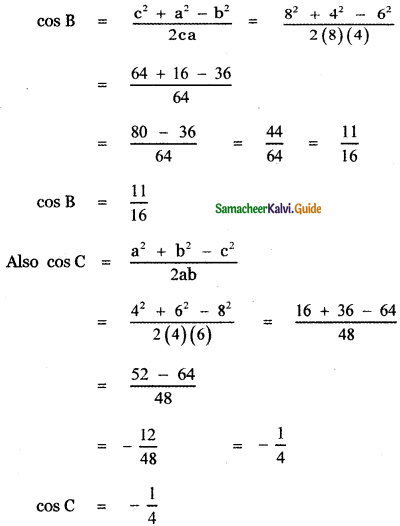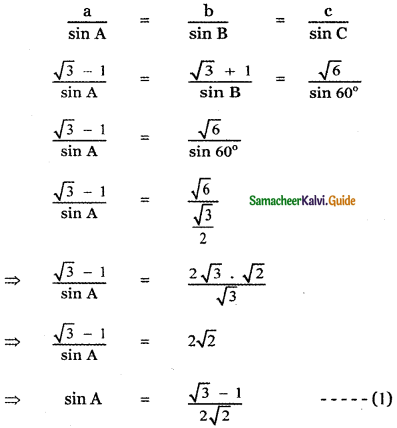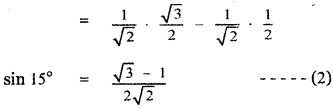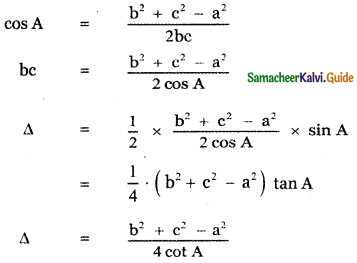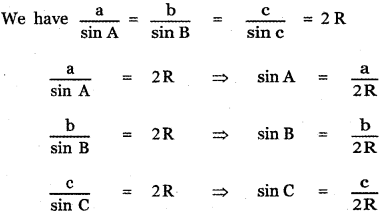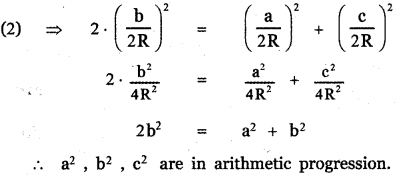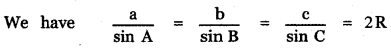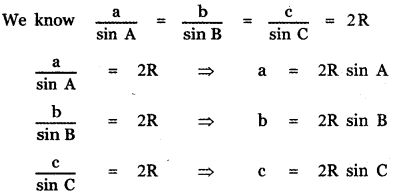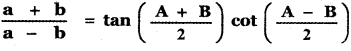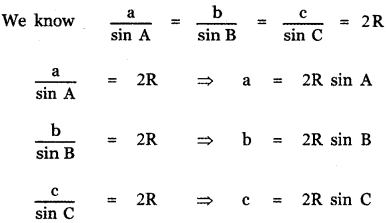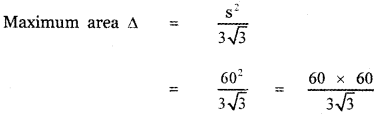Category: Class 11

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 5 Binomial Theorem, Sequences and Series Ex 5.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.1

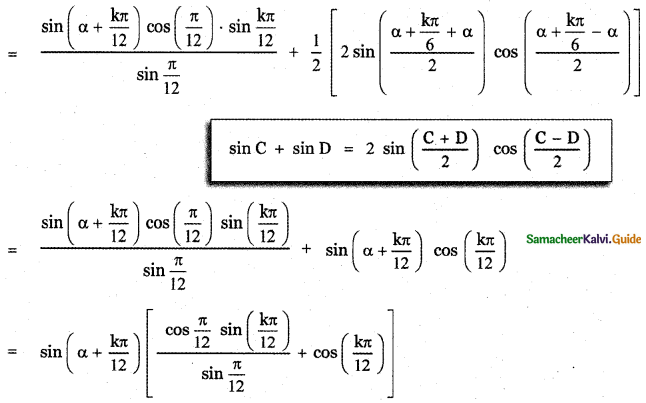
Question 1.
Expand
(i) \(\left(2 x^{2}-\frac{3}{x}\right)^{3}\)
(ii) \(\left(2 x^{2}-3 \sqrt{1-x^{2}}\right)^{4}+\left(2 x^{2}+3 \sqrt{1-x^{2}}\right)^{4}\)
Answer:
(i) \(\left(2 x^{2}-\frac{3}{x}\right)^{3}\)

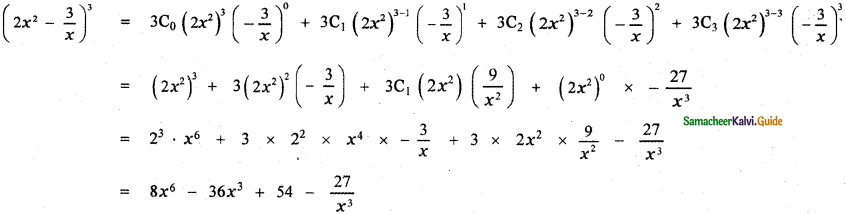
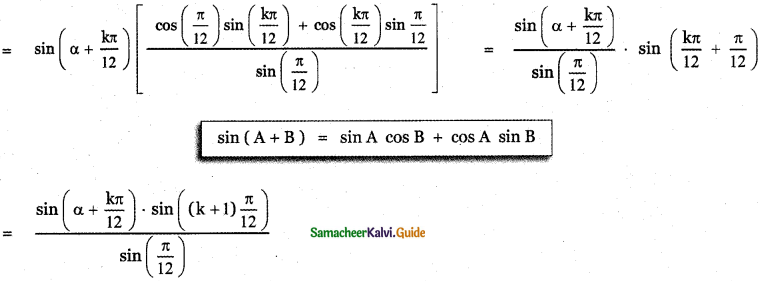
(ii) \(\left(2 x^{2}-3 \sqrt{1-x^{2}}\right)^{4}+\left(2 x^{2}+3 \sqrt{1-x^{2}}\right)^{4}\)

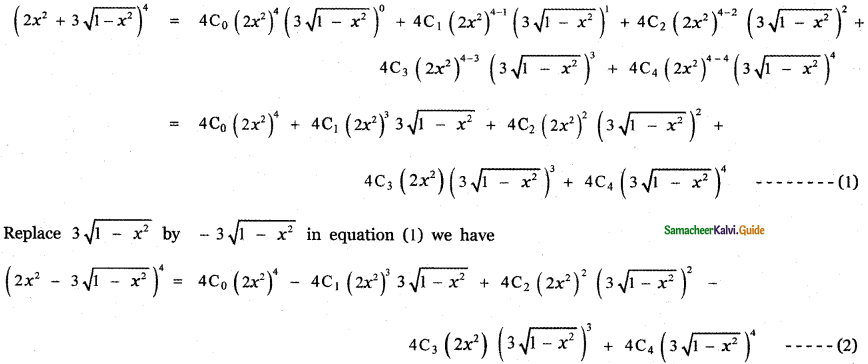
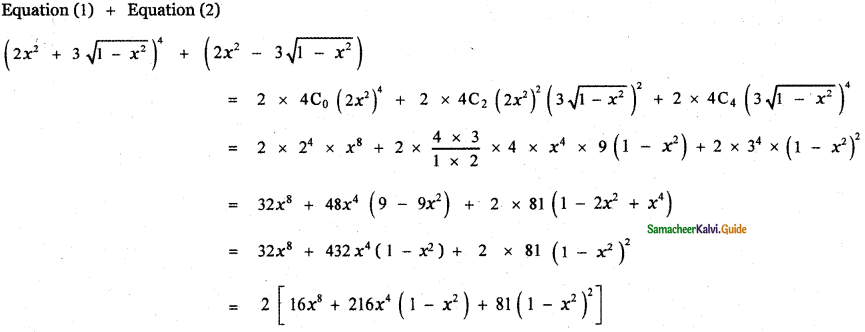
Question 2.
Compute
(i) 102⁴
(ii) 99⁴
(iii) 9⁷
Answer:
(i) 102⁴
102⁴ = (100 + 2)⁴

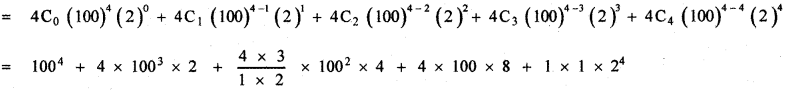
= 100000000 + 8 × 1000000 + 24 × 10000 + 3200 + 16
= 100000000 + 8000000 + 240000 + 3216
= 108243216

(ii) 99⁴
99⁴ = (100 – 1)⁴

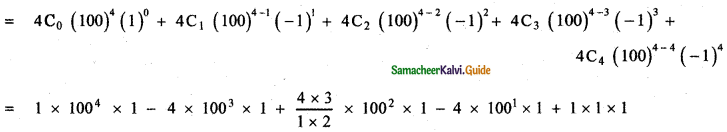
= 100000000 – 4 × 1000000 + 6 × 10000 – 400 + 1
= 100000000 – 4000000 + 60000 -400+1
= 96059601

(iii) 9⁷
9⁷ = (10 – 1)⁷


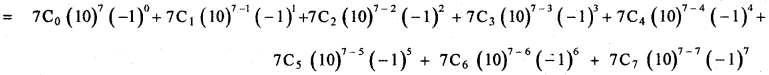
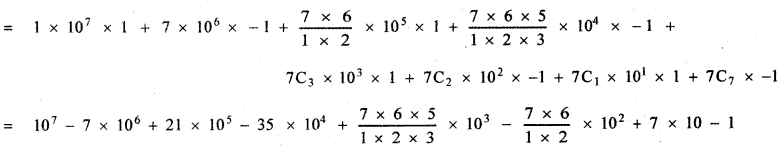
= 10³ (10⁴ – 7 × 10³ + 21 × 10² – 35 × 10 + 35) – 21 × 100 + 70 – 1
= 10³ (10000 – 7000 + 2100 – 350 + 35 ) – 2100 + 70 – 1
= 10³ (12135 – 7350) – 2031
= 10³ × 4785 – 2031
= 4785000 – 2031
= 4782969

Question 3.
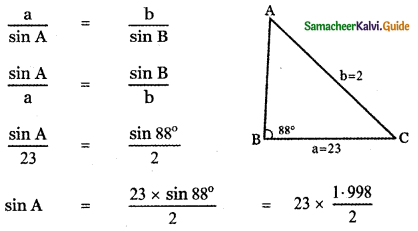
Using binomial theorem, indicate which of the following two number is larger. (l.Ol)1000000, 10000 Answer:

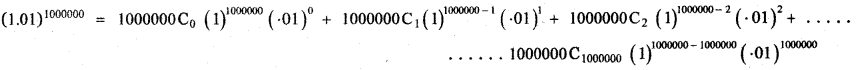
= 1000000C₀ + 1000000C₁( . 01) + …………………….
= 1 + 1000000 × 0 . 01 + ……………………..
= 1 + 10000 + other positive terms
= 10001 + other positive terms
(1.01)^1000000 – 10000 = 10001 + other positive terms – 10000 > 0
∴ (1.01)^1000000 > 10000 ⇒ (1.01)^1000000 is larger.

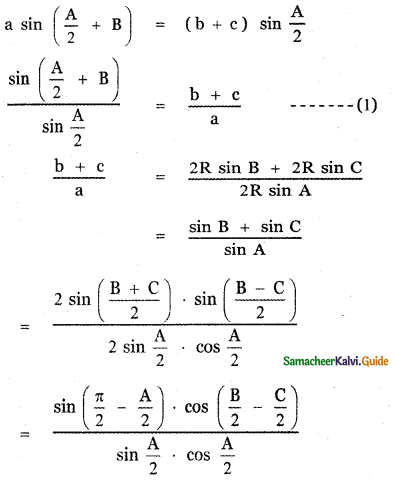
Question 4.
Find the coefficient of x¹⁵ in \(\left(x^{2}+\frac{1}{x^{3}}\right)^{10}\)
Answer:
General term T_r+1 = nC_r x^n-r . a^r
∴ In the expansion \(\left(x^{2}+\frac{1}{x^{3}}\right)^{10}\)

To find the coefficient of x¹⁵, Put 20 – 5r = 15
20 – 15 = 5r ⇒ 5r = 5 ⇒ r = 1
∴ T_{1 + 1} = 10C₁x^{20 – 5} ⇒ T₂ = 10 . x¹⁵
∴ The coefficient of x¹⁵ is 10

Question 5.
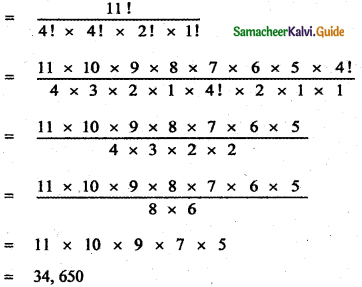
Find the coefficient of x6 and the coefficient of x² in \(\left(x^{2}-\frac{1}{x^{3}}\right)^{6}\)
Answer:
The general terms is T_r+1 = nC_ra^n-r . a^r
∴ The general term in the expansion of \(\left(x^{2}-\frac{1}{x^{3}}\right)^{6}\) is

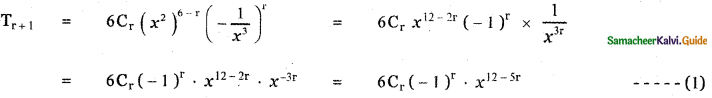
To find the coefficient of x⁶ , Put 12 – 5r = 6
12 – 6 = 5r ⇒ 5r = 6 ⇒ r = \(\frac{6}{5}\) which is impossible.
∴ There is no x⁶ term in the expansion.
To find the coefficient of x²,
Put 12 – 5r = 2
⇒ 12 – 2 = 5r
⇒ 10 = 5r
⇒ r = \(\frac{10}{5}\) = 5
Substituting in (1) we have

T₃ = 15
∴ The coefficient of x² is 15

Question 6.
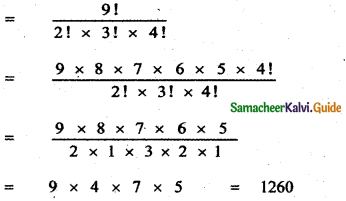
Find the coefficient of x⁴ in the expansion of (1 + x³)⁵⁰ \(\left(x^{2}+\frac{1}{x}\right)^{5}\)
Answer:


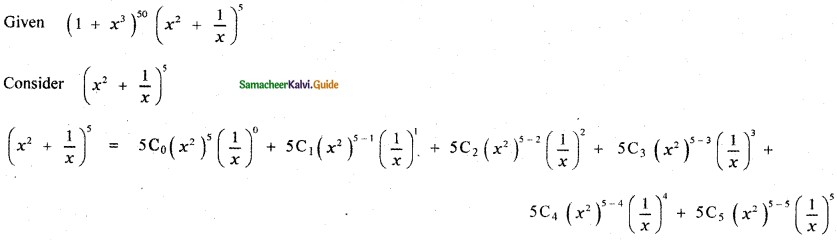
= 10x⁴ × 1 + 5 × 1225 x⁴ + 19600 x⁴ + 500 x⁴
= x⁴ (10 + 6125 + 19600 + 500) = 26235 . x⁴
∴ The coefficient of x⁴ is 26235.

Question 7.
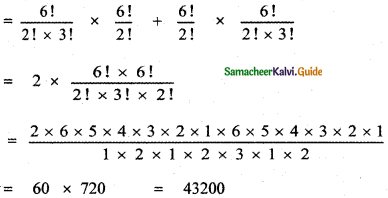
Find the constant term of \(\left(x^{3}-\frac{1}{3 x^{2}}\right)^{5}\)
Answer:


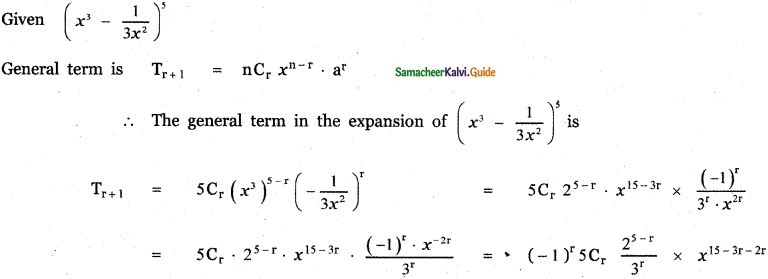
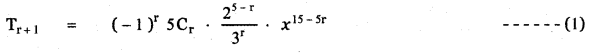
To get the constant term,
Put 15 – 5r = 0
⇒ 5r = 15
⇒ r = 3

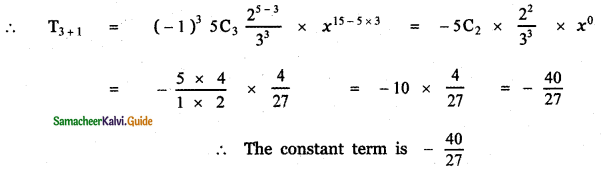
Question 8.
Find the last two digits of the number 3⁶⁰⁰.
Answer:
Consider 3⁶⁰⁰
3⁶⁰⁰ = (3²)³⁰⁰ = 9³⁰⁰ = (1o – 1)³⁰⁰

= 10³⁰⁰ – 300 (10)²⁹⁹ + ………………. + 300 C₁ × 10 × – 1 + 1 × 1 × 1
= 10³⁰⁰ – 300 (1o)²⁹⁹ + …………….. – 300 × 10 + 1
= 10³⁰⁰ – 300 × 10²⁹⁹ + ……………… – 3000 + 1
All the terms except the last are multiples of 100 and hence divisible by 100.
∴ The last two digits will be 01.

Question 9.
If n is a positive integer show that 9ⁿ⁺¹ – 8n – 9 is always divisible by 64.
Answer:

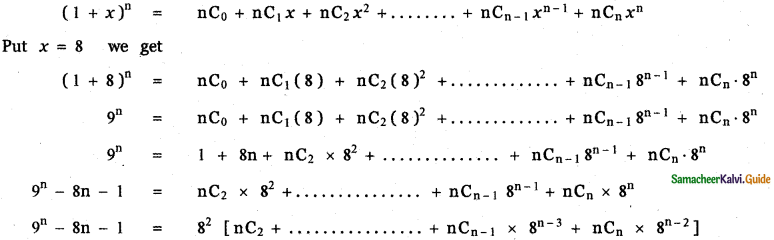
which is divisible by 64 for all positive integer n.
∴ 9ⁿ – 8n – 1 is divisible by 64 for all positive integer n.
Put n = n + 1 we get
9^{n + 1} – 8 (n + 1) – 1 is divisible by 64 for all possible integer n
(9^{n + 1} – 8n – 8 – 1) is divisible by 64
∴ 9^{n + 1} – 8n – 9 is always divisible by 64

Question 10.
If n is an odd positive integer, prove that the coefficients of the middle terms in the expansion of (x + y)ⁿ are equal.
Answer:
Given (x + y)ⁿ
If n is odd the middle term in the expansion of (x + y)ⁿ are \(\frac{T_{n-1}}{2}+1\) and \(\mathrm{T}_{\frac{\mathrm{n}+1}{2}+1}\)

Question 11.
If n is a positive integer and r is a non-negative integer, prove that the coefficients of x^r and x^n-r in the expansion of (1 + x)ⁿ are equal.
Answer:
Given (1 + x)ⁿ.
General term T_r+1 = nC_r x^{n – r} . a^r
∴ The general term in the expansion of (1 + x)ⁿ is T_r+1 = nC_r . (1)^{n – r} . x^r
T_r+1 = nC_r . x^r ……….. (1)
∴ Coefficient of x^r is nC_r,
Put r = n – r in (1)
T_{n – r + 1} = nC_{n – r} . x^n-r
∴ The coefficient of x^n-r is nC_n-r …………. (2)
we know nC_r = nC^n-r
∴ The coefficient of x^r and coefficient of x^n-r are equal, (by (1) & (2))

Question 12.
If a and b are distinct integers, prove that a – b is a factor of aⁿ – bⁿ, whenever n is a positive integer.
Answer:
Let a = a + b – b
= b + (a – b)
aⁿ = [b + (a – b)]ⁿ
Using binomial expansion

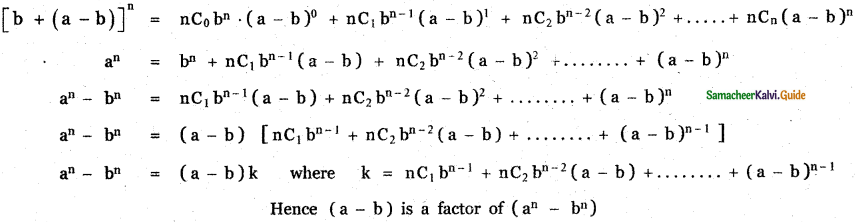
Question 13.
In the binomial expansion of (a + b )n , the coefficients of the 4th and 13th terms are equal to each other , find n.
Answer:
In (a + b)ⁿ general term is t_{r + 1} = ⁿC_r a^{n – r} b^r
So, t₄ = t_{3 + 1} = ⁿC₃ = ⁿC₁₂
⇒ n = 12 + 3 = 15
We are given that their coefficients are equal ⇒ ⁿC₃ = ⁿC₁₂ ⇒ n = 12 + 3 = 15
[ⁿC_x = ⁿC_y ⇒ x = y (or) x + y = n]

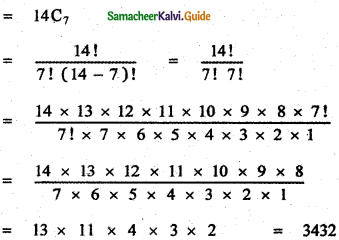
Question 14.
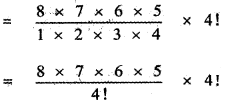
If the binomial co – efficients of three consecutive terms in the expansion of (a + x)ⁿ are in the ratio 1 : 7 : 42, then find n.
Answer:
The general term in the expansion of (a + b)ⁿ is T_r+1 = nC_r . a^n-r . b^r
∴ The general term in the expansion of (a + x)ⁿ is T_r+1 = nC_r . a^n-r . x^r
Let the three consecutive terms be r^th term, (r + 1 )^th term, (r + 2 )^th term.

Question 15.
In the binomial coefficients of (1 + x)ⁿ, the coefficients of the 5^th, 6^th, and 7^th terms are in A.P. Find all values of n.
Answer:
Given (1 + x)ⁿ

12(n – 4) = 30 + n² – 5n – 4n + 20 ⇒ 12n – 48 = 30 + n² – 9n + 20
⇒ n² – 9n – 12n + 50 + 48 = 0 ⇒ n² – 21n + 98 = 0
⇒ n² – 14n – 7n + 98 = 0 ⇒ n(n – 14) – 7(n – 14) = 0
⇒ (n – 7) (n – 14) = 0 ⇒ n = 7 or n = 14

Question 16.
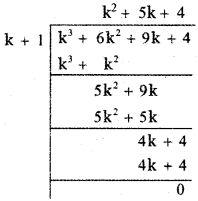
prove that

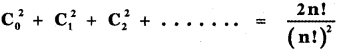
Answer:

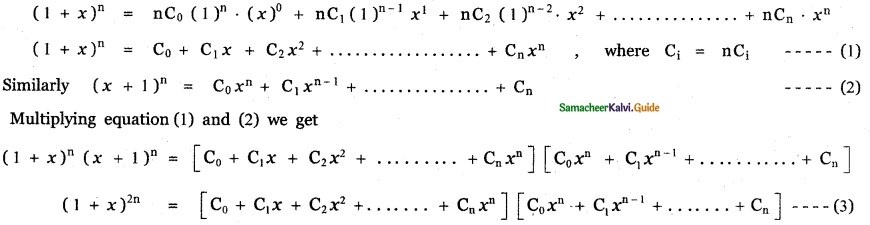
This relation is true for all values of n. Equating coefficient of xⁿ on both sides, we have
The general term in the expansion of (1 + x)²ⁿ is T_{r + 1} = 2nC_r (1)^{2n – r} . x^r
Put r = n we get, T_n+1 = 2nC_n . xⁿ
∴ The coefficient of xⁿ in the expansion of (1 + x)²ⁿ is 2nC_n

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 4 Combinatorics and Mathematical Induction Ex 4.5 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.5

Choose the correct or the most suitable answer:

Question 1.
The sum if the digits at the 10^th place of all numbers formed with the help of 2, 4, 5, 7 taken all at a time is
(1) 432
(2) 108
(3) 36
(4) 18
Answer:
(2) 108

Explaination:

Number of digits given = 2, 4, 5, 7
Number of 4 digit numbers formed = 4! =24
So each digit occur \(\frac{24}{4}\) = 6 times
Sum of the digits = 2 + 4 + 5 + 7 = 18
So sum of the digits in each place = 18 × 6 = 108

Question 2.
In an examination, there are three multiple-choice questions and each question has 5 choices. The number of ways in which a student can fail to get all answer correct is
(1) 125
(2) 124
(3) 64
(4) 63
Answer:
(2) 124

Explanation:
Number of multiple-choice questions = 3
Number of choices in each question = 5
Number of ways of answering = 5 × 5 × 5 = 5³ = 125
Number of ways of getting all answer correct = 1
∴ Number of ways of getting incorrect answer = 125 – 1 = 124

Question 3.
The number of ways in which the following prize be given to a class of 30 boys first and second in mathematics, first and second in Physics, first in Chemistry and first in English is
(1) 30⁴ × 29²
(2) 30² × 29³
(3) 30² × 29⁴
(4) 30 × 29⁵
Answer:
(1) 30⁴ × 29²

Explanation:
I and II in maths can be given in 30 × 29 ways.
I and II in physics can be given in 30 × 29 ways.
I and chemistry can be given in 30 ways.
I in English can be given in 30 ways.
So total number of ways = 30 × 29 × 30 × 29 × 30 × 30 = 30⁴ × 29²

Question 4.
The number of 5 digit numbers all digits of which are odd is
(1) 25
(2) 5⁵
(3) 5⁶
(4) 625
Answer:
(2) 5⁵

Explanation:
The odd digit numbers = 1, 3, 5, 7, 9
Since repetition is allowed, each digit can be filled by 1, 3, 5, 7, 9
Unit’s place can be filled in 5 ways
Ten’s place can be filled in 5 ways etc.
∴ The number of 5 digit numbers with an odd digit in each place = 5 × 5 × 5 × 5 × 5 = 5⁵ ways

Question 5.
In 3 fingers, the number of ways four rings can be worn is ————- ways.
(1) 4³ – 1
(2) 3⁴
(3) 68
(4) 64
Answer:
(4) 64

Explanation:
Each letter can be ported in 3 ways
∴ 4 letter is 3⁴ ways

Question 6.

then the value of n are
(1) 7 and 11
(2) 6 and 7
(3) 2 and 11
(4) 2 and 6
Answer:
(2) 6 and 7

Explaination:

( n + 5 ) ( n + 4) = 2 × 11 × (n – 1)
n² + 5n + 4n + 20 = 22n – 22
n² + 9n + 20 – 22n + 22 = 0
n² – 13n + 42 = 0
n (n – 6) – 7 (n – 6) = 0
(n – 7) (n – 6) = 0
n – 7 = 0 or n – 6 = 0
n = 7 and n = 6

Question 7.
The product of r consecutive positive integers is divisible by
(1) r !
(2) (r – 1) !
(3) ( r + 1 ) !
(4) r^r
Answer:
(1) r !

Explanation:
1(2) (3) ….. (r) = r! which is ÷ by r!

Question 8.
The number of five-digit telephone numbers having at least one of their digits repeated is
(1) 90000
(2) 10000
(3) 30240
(4) 69760
Answer:
(4) 69760

Explaination:
Case (i) When zero is allowed in the first place.
The number of five-digit telephone numbers which can
be formed using the digits 0, 1, 2, …………,9 is 10⁵.
The number of five-digit telephone numbers which have none of their digits repeated is 10P⁵
= 10 × 9 × 8 × 7 × 6 = 30240
∴ The required number of telephone number
= 10⁵ – 30240
= 100000 – 30240
= 69,760

Case (ii) When zero is not allowed in the first place,
(a) Repetition allowed:

The number of ways of filling the first box, second box, …………….. , fifth box
= 9 × 10 × 10 × 10 × 10
= 90000

(b) Repetition riot allowed:
Number of ways of filling 1 box = 9
Number of ways of filling 2^nd box = 9
Number of ways of filling 3^rd box = 8
Number of ways of filling 4^th box = 7
Number of ways of filling 5^th box = 6
∴ Number of numbers with no digit is repeated = 9 × 9 × 8 × 7 × 6 = 37216
∴ Number of numbers having atleast one of the digits repeated = 90000 – 37216 = 52,784

Question 9.
If (a² – a ) C₂ = ( a² – a) C₄ then the value of a is
(1) 2
(2) 3
(3) 4
(4) 5
Answer:
(2) 3

Explaination:
(a² – a)C₂ = (a² – a) C₄
(a² – a)C₂ = (a² – a) C_{(a² – a) – 4} [nC_r = nC_n-r]
(a² – a)C₂ = (a² – a) C_{a² – a – 4}
∴ 2 = a² – a – 4
a² – a – 4 – 2 = 0 ⇒ a² – a – 6 = 0
a² – 3a + 2a – 6 = 0
a (a – 3) + 2 (a – 3) = 0
⇒ (a + 2)(a – 3) = 0 ⇒ a = – 2 or 3

Question 10.
There are 10 points in a plane and 4 of them are collinear. The number of straight lines joining any two points is
(1) 45
(2) 40
(3) 39
(4) 38
Answer:
(2) 40

Explaination:
Total number of points = 10
The number of straight lines joining any two points is same as the number ways of selecting 2 points from 10 points.
∴ The number of straight lines = 10C₂
Given 4 points are collinear.
∴ The number of straight lines that these 4 points contribute = 4C₂
Since 4 points are collinear they lie on a line.
∴ Required number of lines = 10C₂ – 4C₂ + 1

= 5 × 9 – 2 × 3 + 1
= 45 – 6 + 1 = 40

Question 11.
The number of ways in which a host lady invite for a party of 8 out of 12 people of whom two do not want to attend the party together is
(1) 2 × 11C₇ + 10C₈
(2) 11C₇ + 10C₈
(3) 12C₈ – 10C₆
(4) 10C₆ + 2!
Answer:
(3) 12C₈ – 10C₆

Explaination:
Number of people = 12
Number of people invited for the party = 8
Number of people not willing to attend the party = 2
Number of ways of selecting 8 people from 12 people is 12C₈
Two people do not attend party out of 10, remaining people 8 can attend in 10C₆ ways.
∴ Number of ways in which two of them do not attend together = 12C₈ – 10C₆

Question 12.
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines.
(1) 6
(2) 9
(3) 12
(4) 18
Answer:
(4) 18

Explaination:
Number of first set of parallel lines = 4
Number of second set of parallel lines = 3
Number of parallelograms = 4C₂ × 3C₂
= \(\frac{4 \times 3}{1 \times 2} \times \frac{3 \times 2}{1 \times 2}\)
= 6 × 3
= 18

Question 13.
Everybody in a room shakes hands with everybody else. The total number of shake hands is 66. The number of persons in the room is
(1) 11
(2) 12
(3) 10
(4) 6
Answer:
(2) 12

Explaination:
Number of shake hands = 66
Let the number of persons = n
First person shakes hands with the remaining n – 1 persons.
Second person shakes hands with the remaining n – 2 persons.

∴ Total number of shake hands
= (n – 1) + (n – 2) + …………. + 2 + 1
= \(\frac{(\mathrm{n}-1)(\mathrm{n}-1+1)}{2}\)
Given 66 = \(\frac{(\mathrm{n}-1) \mathrm{n}}{2}\)
n² – n = 132
n² – n – 132 = 0
(n – 12) (n + 11) = 0
n = 12 or n = – 11
n = – 11 is not possible.
∴ n = 12

Question 14.
Number of sides of a polygon having 44 diagonals is
(1) 4
(2) 4!
(3) 11
(4) 22
Answer:
(3) 11

Explaination:
Number of diagonals of a polygon with n sides
= nC₂ – n
= \(\frac{n(n-1)}{2}\)
Given \(\frac{n(n-1)}{2}\) – n = 44
n² – n + 2n = 88
n² – 3n – 88 = 0
(n – 11 ) (n + 8) = 0
n = 11 and n = – 8
n = – 8 is not possible.
∴ n = 11

Question 15.
If 10 lines are drawn in a plane such that no two of them are parallel and no three are concurrent, then the total number of point of intersection are
(1) 45
(2) 40
(3) 10!
(4) 210
Answer:
(1) 45

Explaination:
Number of non-parallel lines = 10
Two lines will interest.
∴ Number of points of intersection
= 10C₂ = \(\frac{10 \times 9}{1 \times 2}\) = 45

Question 16.
In a plane there are 10 points are there out of which 4 points are collinear, then the number of triangles formed is
(1) 110
(2) 10C₃
(3) 120
(4) 116
Answer:
(4) 116

Explaination:
Number of points = 10
Number of triangles formed by using 10 points is same as number of ways of choosing 3 points from 10 points = 10C₃
Also given 4 points are collinear.
∴ These 4 points do not contribute triangles.
Thus, total number of triangles = 10C₃ – 4C₃
= \(\frac{10 \times 9 \times 8}{1 \times 2 \times 3}\) – 4
= 5 × 3 × 8 – 4
= 120 – 4
= 116

Question 17.
In 2nC₃ : nC₃ = 11 : 1 then
(1) 5
(2) 6
(3) 11
(4) 7
Answer:
(2) 6

Explaination:
Given 2nC₃ : nC₃ = 11 :

4(2n – 1) = 11 (n – 2)
8n – 4 = 11 n – 22
-4 + 22 = 11 n – 8n
18 = 3n
⇒ n = 6

Question 18.
(n – 1) C_r + ( n – 1 ) C_{r – 1} is
(1) (n + 1) C_r
(2) (n – 1) C_r
(3) nC_r
(4) nC_{r – 1}
Answer:
(3) nC_r

Explaination:
[nC_r + nC_{r – 1} = (n + 1 ) C_r
(n – 1)C_r + (n – 1)C_{r – 1} = (n – 1 + 1) C_r
= nC_r

Question 19.
The number of ways of choosing 5 cards out of a deck of 52 cards which include atleast one king is
(1) 52C₅
(2) 48 C₅
(3) 52C₅ + 48C₅
(4) 52C₅ – 48C₅
Answer:
(4) 52C₅ – 48C₅

Explaination:
Number of cards = 52,
Number of kings = 4
Number of ways of choosing 5 cards out of 52 cards = 52 C₅
Number of cards without kings = 48
Number of ways of choosing 5 cards with no kings from 48 cards = 48 C₅
∴ Number of ways of choosing 5 cards out of 52 cards
= 52C₅ – 48C₅

Question 20.
The number of rectangles that a chessboard has
(1) 81
(2) 9⁹
(3) 1296
(4) 6561
Answer:
(3) 1296

Explaination:
Number of rectangles in a chessboard is

= 36 × 36
= 1296

Question 21.
The number of 10 digit number that can be written by using digits 2 and 3 is
(1) 10C₂ + 9C₂
(2) 2¹⁰
(3) 2¹⁰ – 2
(4) 10!
Answer:
(2) 2¹⁰

Explaination:

Each box can be filled in two ways using digits 2 and 3.
∴ A number of 10 digit number that can be written by using the digits 2 and 3 is 2 × 2 × 2 × …………. 10 times. = 210

Question 22.
If Pr stands for rPr, then the sum of the series 1 + P₁ + 2P₃ + 3P₃ + ……… + nP_n is
(1) P_{n + 1}
(2) P_{n + 1} – 1
(3) P_{n + 1} + 1
(4) (n + 1)P_{n – 1}
Answer:
(1) P_{n + 1}

Explaination:
Given P, = rP_r = r!
1 + 1 × P₁! + 2 × P₂ + 3 × P₃ + …………… + n × P_n!
= 1 + (1 × 1! + 2 × 2! + 3 × 3! + …………. + n × n!)
= (n + 1 )!
= P_{n + 1}
[(1 × 1 !) + (2 × 2!) + (3× 3 !) + ….. + (n × n !) = (n + 1)! – 1]

Question 23.
The product of first n odd natural numbers equals
(1) 2nC_n × nP_n
(2) \(\left(\frac{1}{2}\right)^{n}\) 2nC_n × nP_n
(3) \(\left(\frac{1}{4}\right)^{n}\) × 2nC_n × 2nP_n
(4) nC_n × nP_n
Answer:
(2) \(\left(\frac{1}{2}\right)^{n}\) 2nC_n × nP_n

Explaination:
1 . 3 . 5 …………. (2n – 1)

Question 24.
If nC₄, nC₅, nC₆ are in A. P. the value of n can be
(1) 14
(2) 11
(3) 9
(4) 5
Answer:
(1) 14

Explaination:
Given nC_n, nC₅, nC₆ are in A. P.
∴ 2 × nC₅ = nC₄ + nC₆

12(n – 4) = 30 + (n – 4) (n – 5)
12n – 48 = 30 + n² – 5n – 4n + 20
12n – 48 = 50 + n² – 9n
n² – 9n – 50 – 12n + 48 = 0
n² – 21n + 98 = 0
n² – 14n – 7n + 98 = 0
n(n – 14) – 7(n – 14) = 0
(n – 7) (n – 14) = 0
n – 7 = 0 or n – 14 = 0
n = 7 or n = 14

Question 25.
1 + 3 + 5 + 7 + …………. + 17 is equal to
(1) 101
(2) 81
(3) 71
(4) 61
Answer:
(2) 81

Explaination:
Given 1 + 3 + 5 + 7 + ………… + 17
This is an A.P. with first term a = 1
Common difference d = 2
Last term t_n = 17
a + (n – 1)d = 17
1 + (n – 1)2 = 17
(n – 1)2 = 17 – 1
(n – 1)2 = 16
n – 1 = \(\frac{16}{2}\) = 8
n = 9

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 4 Combinatorics and Mathematical Induction Ex 4.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.4

Question 1.
By the principle of mathematical induction, prove that, for n ≥ 1
1² + 2² + 3² + ……….. + n³ = \(\left(\frac{\mathbf{n}(\mathbf{n}+\mathbf{1})}{2}\right)^{2}\)
Answer:
Let P(n) = 1² + 2² + 3² + ……….. + n³
p(n) = \(\left(\frac{\mathbf{n}(\mathbf{n}+\mathbf{1})}{2}\right)^{2}\)

Step 1:
Let us verify the statement for n = 1
p(1) = 1³ = \(\left(\frac{1(1+1)}{2}\right)^{2}\)

P(1) = 1
∴ The given statement is true for n = 1

Step 2 :
Let us assume that the given statement is true for n = k
P(k) = 1³ + 2³ + 3³ + …………… + k³

Step 3 :
Let us prove the statement is true for n = k + 1
P(k + 1 ) = 1³ + 2³ + 3³ + …………… + k³ + (k + 1)³

This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
1² + 2² + 3² + ……….. + n³ = \(\left(\frac{\mathbf{n}(\mathbf{n}+\mathbf{1})}{2}\right)^{2}\)
is true for all natural numbers n.

Question 2.
By the principle of mathematical induction, prove that, for n ≥ 1

Answer:

Step 1 :
Let us verify the statement for n = 1

∴ The given statement is true for n = 1

Step 2 :
Let us assume that the given statement is true for n = k

Step 3:
Let us prove the statement is true for n = k + 1


This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.

is true for all natural numbers n.

Question 3.
Prove that the sum of the first ’n’ non-zero even numbers is n² + n.
Answer:
Let P(n) : 2 + 4 + 6 +…+2n = n² + n, ∀ n ∈ N

Step 1:
P( 1) : 2 = 1² + 1 = 2 which is true for P( 1)

Step 2:
P(k): 2 + 4 + 6+ …+ 2k = k² + k. Let it be true.

Step 3:
P(k + 1) : 2 + 4 + 6 + … + 2k + (2k + 2)
= k²+ k + (2k + 2) = k² + 3k + 2
= k² + 2k + k + 1 + 1
= (k+ 1)²+ (k + 1)
Which is true for P(k + 1)
So, P(k + 1) is true whenever P(k) is true.

Question 4.
By the principle of mathematical induction, prove that, for n ≥ 1, 1 . 2 + 2 . 3 + 3 . 4 + …………. + n . (n + 1) = \(\frac{\mathbf{n}(\mathbf{n}+1)(\mathbf{n}+2)}{3}\)
Answer:
Let P(n) = 1 . 2 + 2 . 3 + 3 . 4 + ………… + n . (n + 1) = \(\frac{\mathbf{n}(\mathbf{n}+1)(\mathbf{n}+2)}{3}\)

Step 1:
Let us verify the statement for n = 1
P(1) = 1 . 2 = \(\frac{1(1+1)(1+2)}{3}\)
= 1 . 2 = \(\frac{1 \cdot 2 \cdot 3}{3}\)
∴ The result is true for n = 1

Step 2:
Let us assume that the result is true for n = k
P (k) = 1-2 + 2-3 + 3- 4 + + k (k + 1 ) =

Step 3:
Let us prove the result for n = k + 1
P(k + 1) = 1 . 2 + 2 . 3 + 3 . 4 + …………… + k (k + 1) (k + 1) (k + 1 + 1)
P (k + 1) = 1 . 2 + 2 . 3 + 3 . 4 + ………….. + k (k + 1) + (k + 1 ) (k + 2)
P (k + 1 ) = P(k) + (k + 1) (k + 2)

This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1, Hence by the principle of mathematical induction, the result is true for all natural numbers n.
1 . 2 + 2 . 3 + 3 . 4 + ………. + n (n + 1) = \(\frac{\mathrm{n}(\mathrm{n}+1)(\mathrm{n}+2)}{3}\)
is true for all natural numbers n ≥ 1

Question 5.
Using the Mathematical induction, show that for any natural number n ≥ 2,

Answer:
Let

The first stage is n = 2

Step 1:
Let us verify the result for n = 2

∴ The given result is true for n = 2.

Step 2:
Let us assume that the result is true for n = k.

Step 3:
Let us prove the result for n = k + 1


∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n ≥ 2.

is true for all natural numbers n ≥ 2.

Question 6.
Using the Mathematical induction, show that for any natural number n ≥ 2,

Answer:

Step 1:
Since n ≥ 2 the first stage is n = 2
Let us verify the result for n = 2

∴ P (2 ) is true.
The result is true for n = 2.

Step 2:
Let us assume that the result is true for n = k.

Step 3:
Let us prove the result for n = k + 1


This implies p(k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n ≥ 2.

is true for all natural numbers n ≥ 2

Question 7.
Using the mathematical induction, show that for any natural number n,

Answer:

Step 1:
First, let us verify the result for n = 1

∴ The given result is true for n = 1

Step 2:
Let us assume the result for n = k

Step 3:
Let us prove the result for n = k + 1

Factorizing k³ + 6k² + 9k + 4
f (k) = k³ + 6k² + 9k + 4
f(- 1) = (- 1)³ + 6(- 1)² + 9(- 1) + 4
f(- 1) = – 1 + 6 – 9 + 4 = 0
∴ (k + 1) is a factor of f(k)

k³ + 6k² + 9k + 4 = (k + 1) (k² + 5k + 4).
= (k + 1) (k² + 4k + k + 4)
= (k + 1) [k(k + 4) + 1(k + 4)]
= (k + 1) (k + 4) (k + 1)

This implies P(k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.

is true for all natural numbers n

Question 8.
Using the Mathematical induction, show that for any natural number n,

Answer:

Step 1:
First, let us verify the result for n = 1


∴ The result is true for n = 1

Step 2:
Let us assume that the result is true for n = k

Step 3:
Let us prove the result for n = k + 1


This implies P(k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.

Question 9.
Prove by mathematical induction that
1! + (2 × 2 !) + (3 × 3!) +…. .+ (n × n!) = (n + 1)! – 1
Answer:
P(n) is the statement
1! + (2 × 2!) + (3 × 3!) + ….. + (n × n!) = (n + 1)! – 1
To prove for n = 1
LHS = 1! = 1
RHS = (1 + 1)! – 1 = 2! – 1 = 2 – 1 = 1
LHS = RHS ⇒ P(1) is true
Assume that the given statement is true for n = k
(i.e.) 1! + (2 × 2!) + (3 × 3!) + … + (k × k!) = (k + 1)! – 1 is true
To prove P(k + 1) is true
p(k + 1) = p(k) + t_{(k + 1)}
P(k + 1) = (k + 1)! – 1 + (k + 1) × (k + 1)!
= (k + 1)! + (k + 1) (k + 1)! – 1
= (k + 1)! [1 + k + 1] – 1
= (k + 1)! (k + 2) – 1
= (k + 2)! – 1
= (k + 1 + 1)! – 1
∴ P(k + 1) is true
⇒ P(k) is true, So by the principle of mathematical induction P(n) is true.

Question 10.
Using the Mathematical induction, show that for any natural number n, x²ⁿ – y²ⁿ is divisible by x + y.
Answer:
Let P(n) = x²ⁿ – y²ⁿ is divisible by (x + y)
For n = 1
P(1) = x^{2 × 1} – y^{2 × 1} is divisible by (x + y)
⇒ (x + y) (x – y) is divisible by (x + y)
∴ P(1) is true
Let P(n) be true for n = k
∴ P(k) = x^2k – y^2k is divisible by (x + y)
⇒ x^2k – y^2k = λ(x + y) …… (i)
For n = k + 1
⇒ P(k + 1) = x^{2(k + 1)} – y^{2(k + 1)} is divisible by (x + y)
Now x^{2(k + 2)} – y^{2(k + 2)}
= x^{2k + 2} – x^2ky² + x^2ky² – y^{2k + 2}
= x^2k.x² – x^2ky² + x^2ky² – y^2ky²
= x^2k (x² – y²) + y²λ (x + y) [Using (i)]
⇒ x^{2k + 2} – y^{2k + 2} is divisible by (x + y)
∴ P(k + 1) is true.
Thus P(k) is true ⇒ P(k + 1) is true.
Hence by the principle of mathematical induction, P(n) is true for all n ∈ N

Question 11.
By the principle of mathematical induction, prove that, for n ≥ 1, 1² + 2² + 3² + ………….. + n² > \(\frac{n^{3}}{3}\)
Answer:
Let P (n) = 1² + 2² + 3² + ………….. + n² > \(\frac{n^{3}}{3}\)

Step 1:
Let us first verify the result for n = 1

∴ The result is true for n = 1

Step 2:
Let us assume that the result is true for n = k.
P(k) = 1² + 2² + 3² + …………… + k² > \(\frac{\mathrm{k}^{3}}{3}\)

Step 3:
Let us prove the result for n = k + 1
P(k + 1) = 1² + 2² + 3² + …………… + k² + (k + 1)²
P(k + 1) = P(k) + ( k + 1)²

This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
1² + 2² + 3² + ………….. + n² > \(\frac{n^{3}}{3}\)

Question 12.
Use induction to prove that n³ – 7n + 3, is divisible by 3, for all natural numbers n.
Answer:
Let P(n) : n³ – 7n + 3
Step 1:
P(1) = (1)³ – 7(1) + 3
= 1 – 7 + 3 = -3 which is divisible by 3
So, it is true for P(1).

Step 2:
P(k) : k³ – 7k + 3 = 3λ. Let it be true
⇒ k³ = 3λ + 7k – 3

Step 3:
P(k + 1) = (k + 1)³ – 7(k + 1) + 3
= k³ + 1 + 3k² + 3k – 7k – 7 + 3
= k³ + 3k² – 4k – 3
= (3λ + 7k – 3) + 3k² – 4k – 3 (from Step 2)
= 3k² + 3k + 3λ – 6
= 3(k² + k + λ – 2) which is divisible by 3.
So it is true for P(k + 1).
Hence, P(k + 1) is true whenever it is true for P(k).

Question 13.
Use induction to prove that 5^{n + 1} + 4 × 6ⁿ when divided by 20 leaves a remainder 9 , for all natural numbers n.
Answer:
To prove 5^{n + 1} + 4 × 6ⁿ when divided by 20 leaves a remainder 9
That is to prove 5^{n + 1} + 4 × 6ⁿ – 9 is divisible by 20
Let P (n) be the statement 5^{n + 1} + 4 × 6ⁿ
which is divisible by 20
P (n) = 5^{n + 1} + 4 × 6ⁿ – 9 = 20λ

Step 1 :
Let us verify the statement for n = 1
P (1) = 5^{i + 1} + 4 × 6¹ – 9
= 5² + 4 × 6 – 9
= 25 + 24 – 9
= 49 – 9 = 40
which is divisible by 20
∴ The statement is true for n = 1

Step 2:
Let us assume that the statement is true for n = k
P(k) = 5^{k + 1} + 4 × 6^k – 9 is divisible by 20
P(k) = 5^{k + 1} + 4 × 6^k – 9 = 20λ …………… (1)

Step 3:
Let us prove the result for n = k + 1

Hence, P(k + 1) is divisible by 20.
This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
Thus, 5^{n + 1} + 4 × 6ⁿ when divided by 20 leaves a remainder 9, for all natural numbers n.

Question 14.
Use induction to prove that 10ⁿ + 3 × 4^{n + 2} + 5 is divisible by 9, for all natural numbers n.
Answer:
Let P( n) = 10ⁿ + 3 × 4^{n + 2} + 5 is divisible by 9

Step 1:
Let us verify the result for n = 1
P ( 1 ) = 10¹ + 3 × 4^{1 + 2} + 5
= 15 + 3 × 4³
= 15 + 3 × 64
= 15 + 192 = 207
which is divisible by 9
Thus we have verified the result for n = 1

Step 2:
Let us assume the result is true for n = k
P(k) = 10^k + 3 × 4^{k + 2} + 5 is divisible by 9
∴ 10^k + 3 × 4^{k + 2} + 5 = 9m for some m
10^k = 9m – 5 – 3 × 4^{k + 2} for some m

Step 3:
Let us prove the result for n = k + 1

which is divisible by 9
This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
10ⁿ + 3 × 4^{n + 2} + 5 is divisible by 9,
for all natural numbers n.

Question 15.
Prove that using mathematical induction

Answer:

This implies P (k + 1) is true. Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 4 Combinatorics and Mathematical Induction Ex 4.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.3

Question 1.
If nC₁₂ = nC₉ find 21C_n
Answer:
Given nC₁₂ = nC₉
We have nC_x = nC_y ⇒ x = y or x + y = n
nC₁₂ = nC₉
⇒ 12 + 9 = n ⇒ n = 21
⇒ 21C_n = 21C₂₁ = 1

Question 2.
If 15C_{2r – 1} = 15C_{2r + 4}, find F.
Answer:
Given 15C_{2r – 1} = 15C_{2r + 4}
We have nC_x = nC_y ⇒ x = y or x + y = n
15C_{2r – 1} = 15C_{2r + 4}
⇒ (2r – 1) + (2r + 4) = 15
4r + 3 = 15 ⇒ 4r = 12
r = \(\frac{12}{4}\) = 3

Question 3.
If nP_r = 720, If nC_r = 120, find n, r = ?
Answer:
Given nP_r = 720, If nC_r = 120

r ! = 6
r ! = 3 × 2 × 1 = 3!
r = 3

n (n – 1) (n – 2) = 720
n(n – 1) (n – 2) = 1o × 9 × 8
n = 10
∴ r = 3, n = 10

Question 4.
Prove that 15C₃ + 2 × 15C₄ + 15C₅ = 17C₅
Answer:

Question 5.
Prove that 35C₅ + \(\sum_{r=0}^{4}\)(39 – r) C₄ = 40C₅
Answer:

Question 6.
If (n + 1)C₈: (n – 3)P₄ = 57 : 16, find n
Answer:


(n + 1) n(n – 1)(n – 2) = 57 × 7 × 6 × 5 × 4 × 3
= 3 × 19 × 7 × 6 × 5 × 4 × 3
= (7 × 3) × (5 × 4)19 × (6 × 3)
= 21 × 20 × 19 × 18
= (20 + 1) × (20) × (20 – 1) × (20 – 2)
∴ n = 20

Question 7.

Answer:

Question 8.
prove that if 1 ≤ r ≤ n, then n × (n – 1)C_{r – 1} = (n – r + 1) . nC_{r – 1}
Answer:

Question 9.
(i) A kabaddi coach has 14 players ready to play. How many different teams of 7 players could the coach put on the court ?
Answer:
Number of kabaddi players = 14
7 players must be selected from 14 players
Number of ways of selecting 7 players from 14 players is

(ii) There are 15 persons in a party and if each 2 of them shakes hands with each other, how many handshakes happen in the party?
Answer:
Total number of person in the party = 15
Given if each 2 of the 15 persons shakes bands with each other.
∴ The total number of hand shakes is same as the number of ways of selecting 2 persons among 15 persons. This can be done in 15C₂ ways.
Number of hand shakes = 15C₂

(iii) How many chords can be drawn through 20 points on a circle ?
Answer:
Number given points on the circle = 20
A chord is obtained by joining any two points on the circle.‘Number of chords drawn through 20 points is same as the number of ways of selecting 2 points out of 20 points. This can be done 20C₂ ways.
∴ The total number of chords = 20C₂

(iv) In a parking lot one hundred, one year old cars are parked. Out of them five are to be chosen at random for to cheek its pollution devices. How many different set of five cars can be chosen?
Answer:
Number of cars in the parking lot = 100
Number of cars to be selected to check pollution device = 5
Number of ways of selecting 5 cars out of 100 cars

(v) How many ways can a team of 3 boys, 2 girls and 1 transgender be selected from 5 boys, 4 girls and 2 transgenders ?
Answer:
Number of boys = 5
Number of girls = 4
Number of transgender = 2
Number of ways of selecting 3 boys from 5 boys = 5c₃
Number of ways of selecting 2 girls from 4 girls = 4C₂
Number of ways of selecting one transgender from 2 transgenders = 2C₁
Total number of ways of selection

Question 10.
Find the total number of subsets of a set with
(i) 4 elements
(ii) 5 elements
(iii) n elements.
Answer:
(i) Subsets with 4 elements
Number of subsets with no element = 4C_o
Number of subsets with one element = 4C₁
Number of subsets with two elements = 4C₂
Number of subsets with three elements = 4C₃
Number of subsets with four elements = 4C₄
∴ Total number of subsets

(ii) Subsets with 5 elements:
Number of subsets with no element = 5C₀
Number of subsets with one element = 5C₁
Number of subsets with 2 elements = 5 C₂
Number of subsets with 3 elements = 5C₃
Number of subjects with 4 elements = 5C₄
Number of subsets with 5 elements = 5C₅
Total number of subjects

(iii) Subsets with n elements
Number of subsets with no element = nC₀
Number of subsets with 1 , 2 , 3, 4, …………. n elements are nC₁, nC₂, nC₃, nC₄ …………… nC_nrespectively.
∴ Total number of subjects
= nC₀ + nC₁ + nC₂ + nC₃ + ………… + nC_n
= Sum of the coefficients in the binomial expansion (x + a)ⁿ
= 2ⁿ

Question 11.
A Trust has 25 members.
(i) How many ways 3 officers can be selected?
(ii) In how many ways can a president, vice president and a secretary be selected?
Answer:
Number of members in the trust = 25
(i) How many ways 3 officers can be selected?
The number of ways of selecting 3 officers from 25 members is

(ii) In how many ways can a president, vice president, and secretary be selected?
Answer:
From the 25 members, a president can be selected in 25 ways
After the president is selected, 24 persons are left out.
So a Vice President can be selected in (from 24 persons) 24 ways.
After the selection of Vice President, 23 persons are left out
So a secretary can be selected (from the remaining 23 persons) in 23 ways
So a president, Vice president, and a secretary can be selected in ²⁵P₃ ways
²⁵P₃ = 25 × 24 × 23 = 13800 ways

Question 12.
How many ways a committee of six-person from 10 persons can be chosen along with a chairperson and a secretary?
Answer:
Number of persons = 10
Number of committee members to be selected = 6
A committee must have a chairperson and a secretary, the remaining 4 members.
The number of ways of selecting a chairperson and a secretary from 10 persons is

After the selection of chairperson and secretary remaining number of persons = 8
Number of ways of selecting remaining 4 committee members from the remaining 8 persons

= 2 × 7 × 5 = 70
∴ A number of ways of selecting the six committee members from 10 persons.
= 45 × 70 = 3150 ways

Question 13.
How many different selections of 5 books can be made from 12 different books if,
(i) Two particular books are always selected?
Answer:
Total number of books = 12
Number of books to be selected = 5
Given Two books are always selected.
Remaining number of books to be selected = 3
The number of ways of selecting the remaining 3 books from the remaining 10 books = 10C₃

(ii) Two particular books are never selected. Since two books are never selected, the total number of books is 10.
∴ The number of ways of selecting 5 books from 10 books

= 2 × 9 × 2 × 7 = 252 ways

Question 14.
There are 5 teachers and 20 students. Out of them, a committee of 2 teachers and 3 students is to be formed. Find the number of ways in which this can be done. Further, find in how many of these committees
(i) a particular teacher is included?
(ii) a particular student is excluded?
Answer:
The number of teachers = 5
Number of students = 20
The number of ways of selecting 2 teachers from 5 teachers is = 5C₂ ways.

The number of ways of selecting 3 students from 20 students is = 20C₃

= 20 × 19 × 3 = 1140 ways
∴ The total number of selection of the committees with 2 teachers and 5 students is = 10 × 1140 = 11400

(i) A particular teacher is included.
Given a particular teacher is selected. Therefore, the remaining 1 teacher is selected from the remaining 4 teachers. Therefore, the number of ways of selecting 1 teacher from the remaining 4 teacher = 4C₁ ways = 4 ways
The number of ways of selecting 3 students from 20 students = 20C₃


Hence the required number of committees
= 1 × 4 × 1140 = 4560

(ii) A particular student is excluded The number of ways of selecting 2 teachers from 5 teachers is = 5C₂

A particular student is excluded
∴ The number of remaining students = 19
Number of ways of selecting 3 students from 19 students

= 19 × 3 × 17 = 969
∴ The required number of committees = 10 × 969 = 9690

Question 15.
In an examination, a student has to answer 5 questions, out of 9 questions in which 2 are compulsory. In how many ways a student can answer the questions?
Answer:
Total number of questions = 9
Number of questions to be answered = 5
Since 2 questions are compulsory, a student must select 3 questions from dying remaining 7 questions* The number of ways of selecting 3 questions from 7 questions is = 7C₃
∴ The number of ways of answering 5 questions = 7C₃

Question 16.
Determine the number of 5 card combinations out of a check of 52 cards if there is exactly three aces in each combination.
Answer:
Total number of cards in a pack 52
Number of aces = 4
Number of cards to be selected = 5
The number of ways of selecting 3 aces from 4 aces is 4C₃
The number of ways of selecting the remaining 2 cards
from the remaining 48 cards (52 – 4 aces cards) = 48C₂
∴ Required number of ways of selection
= 4C₃ × 48C₂
= 4C₁ × 48C₂

= 4 × 24 × 47 = 4512

Question 17.
Find the number of ways of forming a committee of 5 members out of 7 Indians and 5 Americans, so that always Indians will be the majority in the committee.
Answer:
Number of Indians = 7
Number of Americans = 5
Number of members in the committee = 5
Selection of 5 members committee with majority Indians

Case (i) 3 Indians and 2 Americans
The number of ways of selecting 3 Indians from 7 Indians is = 7C₃
The number of ways of selecting 2 Americans from 5 Americans is = 5C₂
Total number of ways in this case is = 7C₃ × 5C₂

Case (ii) 4 Indians and 1 American
The number of ways of selecting 4 Indians from 7 Indians is = 7C₄
The number of ways of selecting I American from 5 Americans is = 5C₁
The total number of ways, in this case, is = 7C₄ × 5C₁

Case (iii) 5 Indians no American
Number of ways of selecting 5 Indians from
7lndiansis = 7C₅
Total number of ways, in this case, = 7C₅ × 5C₀
∴ Total number of ways of forming the committee


= 7 × 5 × 5 × 24 – 7 × 5 × 5 + 7 × 3
= 350 + 175 + 21 = 546

Question 18.
A committee of 7 peoples has to be formed from 8 men and 4 women. In how many ways can this be done when the committee consists of
(i) Exactly 3 women?
(ii) Atleast 3 women?
(iii) Almost 3 women?
Answer:
Number of men = 8
Number of women = 4
Number of peoples in the committee = 7

(i) Exactly 3 women
In a 7 member committee, women must be 3. Therefore, the remaining 4 must be men.
The number of ways of selecting 3 women from 4 women = 4C₃
The number of ways of selecting 4 men from 8 men = 8C₄
∴ The total number of ways of selection is = 4C₃ × 8C₄

= 8 × 7 × 5 = 280

(ii) At least 3 women
The 7 members committee must contain atleast 3 women
∴ We have the following possibilities
(i) 4 women + 3 men
(ii) 3 women + 4 men

case (i) 4 women + 3 men
The number ways of selecting 4 women .from
4 women is = 4C₄ = 1 way
The number of ways of selecting 3 men from 8 men = 8C₃

∴ The total number of ways = 1 × 56 = 56

case (ii) 3 women + 4 men
The number of ways of selecting 3 women from 4 women is = 4C₃
The number of ways of selecting 4 men from 8 men is = 8C₄
∴ The total number of ways = 4C₃ × 8C₄

= 8 × 7 × 5 = 280
∴ The required number of ways of forming the committee = 56 + 280 = 336

(iii) atmost 3 women
The 7 members must contain at most 3 women,
∴ we have the following possibilities
(i) No women + 7 men
(ii) 1 women + 6 men
(iii) 2 women + men
(iv) 3 women + 4 men

Case (i) 0 women + 7 men
The number of ways of selecting O women from 4 women is = 4C₀
The number of ways of selecting 7 men from 8 men is = 8C₇
Total number of ways = 4C₀ × 8C₇

Case (ii) 1 women + 6 men
The number of ways of selecting 1 woman from 4 women is = 4C₁
The number of ways of selecting 6 men from 8 men is = 8C₆
Total number of ways = 4C₁ × 8C₆

Case (iii) 2 women + 5 men
The number of ways of selecting 2 women from 4 women is = 4C₃
The number of ways of selecting 4 men from 8 men is = 8C₄
∴ Total number of ways = 4C₃ × 8C₄
∴ The required number of ways of forming the committee

Question 19.
7 relatives of a man comprise 4 ladies and 3 gentlemen, his wife also has 7 relatives: 3 of them are ladies and 4 gentlemen. In how many ways can they invite a dinner party of 3 ladies and 3 gentlemen so that there are 3 of the men’s relatives and 3 of the wife’s relatives?
Answer:
Number of relatives of a man = 7
4 ladies and 3 gentlemen
Number of relatives of the man’s wife = 7
3 ladies and 4 gentlemen
The dinner party consists of 3 ladies and 3 gentlemen.
For the dinner party, 3 persons from the man’s relatives and 3 persons from the man’s wife’s relatives are invited.
Then we have the following possibilities for the different possible arrangements.

Required number of ways

Question 20.
A box contains two white balls, three black balls, and four red balls. In how many ways can three balls be drawn from the box, if atleast one black ball is to be included in the draw?
Answer:
Number of white balls = 2
Number of black balls = 3
Number of red balls = 4
Number of balls drawn = 3 balls with atleast 1 blackball
We have the following possibilities


Required number of ways of drawing 3 balls with atleast one black ball.

Question 21.
Find the number of strings of 4 letters that can be formed with the letters of the word EXAMINATION.
Answer:
There are 11 fetters in the word EXAMINATION,
They are AA, II, NN, E, X, M, T, O The four-letter strings may have
(i) 2 alike letters of one kind and 2 alike tetters of the second kind.
(ii) 2 alike fetters and 2 different letters.
(iii) All different fetters.

(i) 2 alike letter of one kind and 2 alike letters of the second kind:
There are three sets of 2 alike letters AA, II, NN. Out of these sets, two sets can be selected in 3C₂ ways. So there are 3C₂ groups each of which còntains 4 letter
strings out of which 2 are alike of one kind type and 2 are alike of the second type.
4 letters in each group can be arranged in \(\frac{4 !}{2 ! \times 2 !}\) ways.
Hence the total number of strings consisting of two alike letters of one kind and 2 alike letters of the second kind

(ii) 2 alike letter and 2 different letters:
Out of sets of two alike letters, one set can be chosen in 3C₁ ways. From the remaining 7 distinct letters, 2 letters can be chosen in 7C₂ ways. Thus 2 alike letters and 2 different letters can be selected in (3C₁ × 7C₂) ways. There are ( 3C₁ × 7C₂) groups of 4 letters each. Now letters of each group can be arranged among themselves in \(\frac{4 !}{2 !}\) ways.

Hence the total number of strings consisting of 2 alike and 2 distinct letters,

(iii) All different letters
There are 8 different letters
E, X, A, M, I, N, T, O

Out of which 4 can be selected in 8C₄ ways. So there are 8C₄ groups of 4 letters each The letter in each of 8C₄ groups’ can be arranged in 4! ways.
∴ The total number of 4. letter strings in which all letters are distinct = 8C4 × 4!

= 56 × 30 = 1680 strings
Hence the total number of 4 letter strings
= 18 +756 + 1680
= 2454 strings

Question 22.
How many triangles can be formed by joining 15 points on the plane, in which no line joining any three points?
Answer:
Number of points 15
To form a triangle we need 3 non – collinear points.
The number of ways of se1ecting 3 non-collinear points from 15 points is = 15C₃

Question 23.
How many triangles can be formed by 15 points of which 7 of them 11e on one line and the remaining 8 on another parallel ‘line?
Answer:
To form a triangle we need 3 non-collinear points. Take the 7 points lying on one line be group A and the remaining 8 points lying on another parallel line be group B.
We have the following possibilities

∴ Required number of ways of forming the triangle

Question 24.
There are 11 points in a plane. No three of these lie in the same straight line except 4 points which are collinear. Find
(i) The number of straight lines obtained from the pairs of these points?
(ii) The number of triangles that can be formed which the vertices as their points.
Answer:
Number of points in a plane = 11
No three of these points lie in the same straight line except 4 points.

(i) The number of straight lines that can be obtained from the pairs of these points
Through any two points, we can draw a straight line.
∴The number straight lines through any two points of the given 11 points = 11C₂

Given that 4 points are collinear. The number of straight lines through any two points of these 4 points is

Since these 4 points are collinear, these 4 points contribute only one line instead of the 6 lines.
The total number of straight lines that can be drawn through 11 points on a plane with 4 of the points being collinear is = 55 – 6 + 1 = 50

(ii) The number of triangles that can be formed for which the points are their vertices.
To form a triangle we need 3 non – collinear points. We have the following possibilities.

(a) If we take one point from 4 collinear points and 2 from the remaining 7 points and join them.

The number of ways of selecting one point from the 4 collinear points is = 4C₁ ways
The number of ways of selecting 2 points from the remaining 7 points is = 7C₂
The total number of triangles obtained in this case is = 4C₁ × 7C₂
∴ The total number of triangles obtained in this case is

(b) If we select two points from the 4 collinear points and one point from the remaining 7 points then the number of triangles formed is

(c) If we select all the three points from the 7 points then the number of triangles formed is

∴ The total number of triangles formed are
= 84 + 42 + 35 = 161

Question 25.
A polygon has 90 diagonals. Find the number of sides.
Answer:
Let the number sides of the polygon be n.
The number of diagonals of a polygon with n sides = \(\frac{n(n-3)}{2}\)
Given \(\frac{n(n-3)}{2}\) = 90
n² – 3n = 180
n² – 3n = 180
n² – 3n – 180 = 0
n² – 15n + 12n – 180 = 0
n (n – 15 ) + 12 (n – 15) = 0
(n + 12) (n – 15) = 0
n + 12 = 0 or n – 15 = 0
n = – 12 or n = 15
But n = – 12 is not possible
∴ n = 15
∴ The number of sides of the polygon having 90 diagonals is 15.

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 4 Combinatorics and Mathematical Induction Ex 4.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.2

Question 1.
If (n – 1)P₃ : nP₄ = 1 : 10 find n.
Answer:
Given (n – 1)P₃ : nP₄ = 1 : 10

Question 2.
If 10P_{r – 1} = 2 × 6P_r, find r.
Answer:
Given 10P_{r – 1} = 2 × 6P_r

5 × 9 × 8 × 7 = (11 – r) (10 – r) (9 – r) (8 – r) (7 – r)
5 × 3 × 3 × 2 × 4 × 7 = (11 – r) (10 – r) (9 – r) (8 – r)(7 – r)
7 × 6 × 5 × 4 × 3 = ( 11 – r ) (10 – r) (9 – r) (8 – r) (7 – r)
(11 – 4) (10 – 4) (9 – 4) (8 – 4) (7 – 4)
= (11 – r) (10 – r) (9 – r) (8 – r) (7 – r)
∴ r = 4

Question 3.
(i) Suppose 8 people enter an event in a swimming meet. In how many ways could the gold, silver and bronze prizes be awarded?
Answer:
From 8 persons we have to select and arrange 3 which can be done in ⁸P₃ ways So the prizes can be awarded in ⁸P₃ = 8 × 7 × 6 = 336 ways

(ii) Three men have 4 mats, 5 waist coats and 6 caps.In how many ways can they wear them?
Answer:
Number of men = 3
Number of coats = 4
Number of waist coats = 5
Number of caps = 6
4 coats can be given to 3 men in 4P₃ ways.
5 waist coats can be given to 3 men in 5P₃ ways.
6 caps can be given to 3 men in 6P₃ ways.
∴ Total number of ways of wearing 3 coats, 4 waist coats and 6 caps is
= 4P₃ × 5P₃ × 6P₃

= 1, 72, 800

Question 4.
Determine the number of permutations of the letters of the word SIMPLE If all are taken at a time?
Answer:
SIMPLE
Total Number of letters = 6
They can be arranged in 6! ways
∴ The number of words = 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720

Question 5.
A test consists of 10 multiple choice questions. In how many ways can the test be answered if
(i) Each question has four choices ?
(ii) The first four questions have three choices and the remaining have five choices?
(iii) Question number n has n + 1 choices ?
Answer:
Each question has 4 choices. So each question can be answered in 4 ways.
Number of Questions = 10
So they can be answered in 410 ways

(ii) The first four questions have 3 choices. So they can be answered in 3⁴ ways.
The remaining 6 questions have 5 choices. So they can be answered in 5⁶ ways.
So all 10 questions can be answered in 3⁴ × 5⁶ ways.

(iii) Given question n has n + 1 choices
question 1 has 1 + 1 = 2 choices
question 2 has 2 + 1 = 3 choices
question 3 has 3 + 1 = 4 choices
question 4 has 4 + 1 = 5 choices
question 5 has 5 + 1 = 6 choices
question 6 has 6 + 1 = 7 choices
question 7 has 7 + 1 = 8 choices
question 8 has 8 + 1 = 9 choices
question 9 has 9 + 1 = 10 choices
So the number of ways of answering all the 10 questions = 2 × 3 × 4 ×…. × 11 = 11! ways

Question 6.
A student appears in an objective test which contain 5 multiple choice, questions. Each question has 4 choices, out of which one correct answer.
(i) What is the maximum number of different answers can the students give?
(ii) How,will the answer change if each question may have more than one correct answer ?
Answer:
(i) What is the maximum number of different answers can the students give?
Selecting a correct answer from the 4 answers can be done in 4 ways.
Total number of questions = 5 So they can be answered in 45 ways

(ii) How will the answer change if each question may have more than one correct answers? Since each question may have more than one correct answer, each question can have the possibilities 1, 2, 3 or 4 correct answers.
∴ Number of ways of answering each question
= 4C₁ + 4C₂ + 4C₃ + 4C₄

= 4 + 6 + 4 + 1 = 15
Thus, the answer will change as 15⁵ (i.e, Total number of ways of answering five questions).

Question 7.
How many strings can be formed from the letters of the word ARTICLE, so that vowels occupy even places?
Answer:
ARTICLE
Vowels A, I, E = 3
Total number of places = 7
1 2 3 4 5 6 7
Number of even places = 3
3 Vowels can occupy 3 places in 3! = 3 × 2 × 1 = 6 ways
Then the remaining 4 letters can be arranged in 4! ways
So total number of arrangement = 3! × 4! = 6 × 24 = 144 ways

Question 8.
8 women and 6 men are standing in a line.
(i) How many arrangements are possible if any individual can stand in any position ?
(ii) In how many arrangements will all 6 men be standing next to one another?
(iii) In how many arrangements will no two men be standing next to one another?
Answer:
Number of women standing in a line = 8
Number of men standing in a line = 6

(i) How many arrangements are possible if any individual can stand In any position?
Total number of persons = 8 + 6 = 14
They can be arranged in 14! ways

(ii) In how many arrangements will all 6 men be standing next to one another?
There are 6 men and 8 women. To make all 6 men together treat them as 1 unit. Now there are 1 + 8 = 9 persons.
They can be arranged in 9! ways. After this arrangement, the 6 men can be arranged in 6! ways.
So total number of arrangements = 9! × 6!

(iii) In how many arrangements will no two men be standing next to one another?

8 women placed in the box can be arranged in 8P₈ = 8! ways
∴ Total number of ways = 9P₆ × 8!

Question 9.
Find the distinct permutations of the letters of the word MISSISSIPPI.
Answer:
The given word is MISSISSIPPI.
Number of letters in the word = 11
Number of S’s = 4
Number of I’s = 4
Number of P’s = 2
Number of M’s = I
Hence the total number of distinct words

Question 10.
How many ways can the product a2 b3 c4 be expressed without exponents?
Answer:
The given term is a²b³c⁴
The factors are a, b, c
Number of a’s = 2
Number of b’s = 3
Number of c’s = 4
a²b³c⁴ = a×a × b×b×b × c×c×c×c
Total number of factors in the product = 9
Number of ways the product can be expressed without exponents

Question 11.
In how many ways 4 mathematics books, 3 physics books, 2 chemistry books and 1 biology book can be arranged on a shelf so that all books of the same subjects are together:
Answer:
Number of maths book = 4
Number of physics books = 3
Number of chemistry books = 2
Number of biology books = 1
Since we want books of the same subjects together, we have to treat all maths books as 1 unit, all physics books as 1 unit, all chemistry books as 1 unit, and all biology books as 1 unit.
Now the total number of units = 4
They can be arranged in 4! ways. After this arrangement.
4 maths book can be arranged in 4! ways
3 physics book can be arranged in 3! ways
2 chemistry book can be arranged in 2! ways and 1 biology book can be arranged in 1! way
∴ Total Number of arrangements 4! 4! 3! 2! = 6912

Question 12.
In how many ways can the letters of the word SUCCESS he arranged so that all S’s are together?
Answer:
SUCCESS
Number of letters = 7
Number of ‘S’ = 3
Since we want all ‘S’ together treat all 3 S’s as 1 unit.
Now the remaining letters = 4
∴ Total number of unit = 5
They can be arranged in 5! ways of them C repeats two times.
So total number of arrangements = \(\frac{5 !}{2 !}\) = 60

Question 13.
A coin is tossed 8 times.
(i) How many different sequences of heads and tails are possible?
Answer:
(i) How many different sequences of heads and tails are possible?
A coin on tossing has two outcomes.
Tossing a coin once number of outcomes = 2
∴ Tossing a coin 8 times number of outcomes = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2⁸
∴ The different sequences of heads and tails are 2⁸

(ii) How many different sequences containing six heads and two tails are possible?
Answer:
When tossing a coin, the possible outcomes are head
and tail, Total number of outcomes of heads and tails
on tossing a coin 8 times is
= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2⁸
The number of ways of getting six heads and 2 tails

= 4 × 7 = 28 ways

Question 14.
How many strings are there using the letters of the word INTERMEDIATE, if
(i) Vowels and consonants are alternative
(ii) All the vowels are together
(iii) Vowels are never together
(iv) No two vowels are together
Answer:
The given word is INTERMEDIATE
Number of letters = 12
Number of I’S = 2
Number of T’S = 2
Number of E’S = 3
Vowels are A,I, I, E, E, E
Total number of vowels = 6
Consonants are N , T, R, M , D , T
Total number of consonants = 6

(i) Vowels and consonants are alternative

(a) Let the first box be filled with a vowel. There are six alternate places available for 6 vowels.
∴ Number of ways of filling 6 vowels in the alternative six boxes is \(\frac{6 !}{2 ! \times 3 !}\)

Remaining 6 boxes can be filled with the 6 consonants. Number of ways of filling the 6 consonants in the remaining 6 boxes is \(\frac{6 !}{2 !}\)

Total number of ways = \(\frac{6 !}{2 ! \times 3 !} \times \frac{6 !}{2 !}\)

(b) Let the first box be filled with a consonant. There six alternate places available for 6 consonants.
∴ Number of ways of filling 6 consonants in the six alternate boxes is \(\frac{6 !}{2 !}\)
Remaining 6 boxes can be filled with the 6 vowels
∴ Number of ways of filling the 6 vowels in the remaining 6 boxes is \(\frac{6 !}{2 ! \times 3 !}\)
Total number of ways = \(\frac{6 !}{2 !} \times \frac{6 !}{2 ! \times 3 !}\)
∴ Total number of strings formed by using the letters of the word INTERMEDIATE, if the vowels and consants are alternative

(ii) All the vowels are together.
Take all the vowels as 1 unit.
Remaining consonants = 6
Total number of units for arrangement = 7
Number of arrangements = \(\frac{7 !}{2 !}\)
(Since in the consonant’s T’ s repeated twice)

Among the vowels, the number of arrangements

∴ Total number of arrangements = 2520 × 60
= 151200

(iii) Vowels are never together :
Total number of arrangements using all the

Number of arrangements where all the vowels are together = 151200
Number of arrangements where all vowels are never together = Total number of arrangements – number of arrangements where the vowels are together = 19958400 – 151200 = 19807200

(iv) No two vowels are together:
same as (i)
The number of strings using the letters of the word INTERMEDIATE if no two vowels are together is 43,200.

Question 15.
Each of the digits 1,1,2,3,3 and 4 is written on a separate card. The six cards are then laid out in a row to form a 6 digit number.
(i) How many distinct 6-digit numbers are there?
Answer:
(i) How many distinct 6-digit numbers are there?
Given numbers are 1, 1, 2, 3, 3, 4
Here 1 occurs twice, 3 occurs twice.
∴ Number of distinct 6 – digit numbers

(ii) How many of these 6-digit numbers are even?
Answer:
The given numbers are 1, 1, 2, 3, 3, 4

In order to get even 6 – digit numbers, the unit place must be filled by the digits 2 or 4. Therefore, the unit place can be filled in 2 ways using the digits 2 or 4. In the remaining 5 digits (excluding the digit placed in the unit place 2 or 4) 1 occurs 2 times, 3 occurs 2 times.
∴ The number of ways of filling other places using
the remaining 5 digit is = \(\frac{5 !}{2 ! \times 2 !}\)
∴ Number of distinct 6 – digit numbers = \(\frac{5 !}{2 ! \times 2 !} \times 2\)

= 5 × 4 × 3
= 60

(iii) How many of these 6 – digit numbers are divisible by 4?
Answer:
In order to get the 6 – digit number divisible by 4, the last two digits must be divisible by 4
∴ The last two digits should be 12 or 24 or 32

Let the last box be filled with 24. The remaining 4 boxes can be filled with the remaining digits

Let the last box be filled with 12. The remaining 4 boxes can be filled with the remaining digits

Let the last box be filled with 32. The remaining 4 boxes can be filled with the remaining digits
The total number of 6 digit numbers which are divisible by 4 is


= 6 + 12 + 12 = 30
∴ Required number of 6 – digit numbers = 30

Question 16.
If the letters of the word GARDEN are permuted in all possible ways and the strings thus formed are arranged in the dictionary order, then find the ranks of the words
(i) GARDEN
(ii) DANGER.
Answer:
(i) GARDEN
The letters of the word arranged in the dictionary order is
A, D, E, G, N, R
Total number of letters = 6
The number of words begins with A = 5!
The number of words begins with D = 5!
The number of words begins with E = 5!
The number of words beginning with G = 5!
(But one of these words is GARDEN)
The number of words beginning with GAD = 3!
The number of words beginning with GAE = 3!
The number of words beginning with GAN = 3!
There are 3 ! words beginning with GAR one of these words is GARDEN. The first word beginning with GAR is the word GARDEN.
∴ The rank of the word GARDEN 3 × 120 + 3 × 6 + 1 = 360 + 18 + 1 = 379

(ii) DANGER
The dictionary order of the letters of the given word is A, D, E, G, N, R
In the dictionary order of words which begin with A, comes first. If we fill the first place with A, the remaining 5 letters can be arranged in 5! ways. Proceeding like this
Number of words beginning with D = 5! = 120
Number of words beginning with DAE = 3! = 6
Number of words beginning with DAG = 3! = 6
Number of words beginning with DANE = 2! = 2
Number of words beginning with DANGE = 1! = 1
(which is the word DANGER)
∴ The rank of the word DANGER = 120 + 6 + 6 + 2 + 1 = 135

Question 17.
Find the number of strings that can be made using all letters of the word THING. If these words are written in dictionary order, what will be the 85th string?
Answer:
The given word is THING
Arranging the letters of the word in the dictionary order, we have G, H, I, N, T
The number of strings that can be made using all the letters T, H, I, N, G of the word THING is = 5! = 120
The number of words beginning with G = 4!
The number of words beginning with H = 4!
The number of words beginning with I = 4!
Number of words so far formed = 4! + 4! + 4!
= 24 + 24 + 24 = 72 words
As the required word is in the 85^th position, the required word must begin with N Number of words beginning with NG = 3!
A number of words beginning with NH = 3!
Total number of words so far formed
= 72 + 3! + 3!
= 72 + 6 + 6
= 84 words
The next string is the required string. It should begin with NI and its first word beginning with NI which is NIGHT
∴ 85^th strings are NIGHT

Question 18.
If the letters of the word FUNNY are permuted in all possible ways and the strings thus formed are arranged in the dictionary order, find the rank of the word FUNNY.
Answer:
The given word is FUNNY
To find the rank of the word FUNNY, write down the letters of the word FUNNY. Other than F in alphabetical order N, N, U, Y
Number of words beginning with F = \(\frac{4 !}{2 !}\)

Among these words, the number of words beginning with FN = 3! = 1 × 2 × 3 = 6words
(Treating FN as one unit, the remaining 3 letters can be arranged in 3 ! ways)
The number of words beginning with FU is = \(\frac{3 !}{2 !}\)

Among these three words, FUNNY is the first word, hence among the twelve words beginning with F, FUNNY appears as the 7^th word.

Question 19.
Find the sum of all 4 – digit numbers that can be formed using digits 1,2,3,4 and 5 repetitions not allowed?
Answer:
The given numbers are 1, 2 , 3 , 4 , 5
The total number of arrangements. Using the digits 1, 2, 3, 4 and 5 taking 4 at a time is 5 P₄
= 5 × 4 × 3 × 2 = 120
∴ 120 four-digit numbers can be formed using the given 5 digits without repetition. To find the sum of these numbers, we will find the sum of digits at unit’s, ten’s, hundred’s and thousand’s place in all these 120 numbers.

Consider the digit in unit’s place. In all these numbers, each of these digits 1, 2 , 3 , 4, 5 occurs 120
in \(\frac{120}{5}\) = 24 times in the units place.
∴ The sum of the digits at unit’s place
= 24(1 + 2 + 3 + 4 + 5)
= 24 × 15 = 360
Similarly sum of the digit’s at ten’s place = 360
Sum of the digit’s at hundred’s place = 360
Sum of the digit’s at thousand’s place = 360
∴ Sum of all four digit numbers formed using the digit’s 1 , 2 , 3 , 4 , 5
= 360 × 10° + 360 × 10¹ + 360 × 10² + 360 × 10³
= 360 (10° + 10¹ + 10² + 10³)
= 360 (1 + 10 + 100 + 1000)
= 360 × 1111
= 3,99,960

Question 20.
Find the sum of all 4 – digit numbers that can be formed using digits 0,2,5,7,8 without repetition.
Answer:
The given digits are 0, 2, 5, 7, 8

The first box can be filled in 4 ways using the digits 2, 5, 7, 8 ( excluding 0). The second box can be filled in 4 ways using the digits 0, 2, 5, 7, 8 excluding the digit placed in the first box. The third box can be filled in 3 ways using the digits 0, 2, 5, 7, 8 excluding the digits placed in the first two boxes. The fourth box can be filled in 2 ways using the digits 0, 2, 5, 7, 8 excluding the digits placed in the first three boxes.
∴ Total number of 4-digit numbers = 4 × 4 × 3 × 2 = 96
To find the sum of all these four-digit numbers.

Fix the number 0 in the list box (4). With the remaining numbers 2, 5, 7, 8, box – 3 can be filled in 4 ways, box – 2 can be filled in 3 ways, and box – 1 can be filled in 2 ways.
∴ Total number of 4 digit numbers ending with 0 is = 4 × 3 × 2 = 24 numbers

Fix the number 2 in the last box -4. With the remaining digits 0, 5, 7, 8. Box -l can be filled in 3 ways excluding the digit 0. Box – 2 can be filled in 3 ways using the digits 0, 5, 7, 8 excluding the digit placed in a box – 1. Box – 3 can be filled in 2 ways using the digits 0, 5, 7, 8 excluding the digits placed in box-1 and box-2.
∴ Total number of 4 – digit numbers ending with the digit 2 = 3 × 3 × 2 = 18 numbers
Similarly, Total numbers of 4 – digit numbers ending with the digit 5 = 18 numbers
Total number of 4 – digit numbers ending with the digit 7 = 18 numbers
Total number of 4 – digit numbers ending with the digit 8 = 18 numbers
∴ Total for unit place = (24 × 0) + (18 × 2) + (18× 5) + ( 18 × 7) +( 18 × 8)
= 18 × (2+ 5 + 7 + 8)
= 18 × 22 = 396
∴ Sum of the digits at the unit place = 396
Similarly Sum of the digits at ten’s place = 396
Sum of the digit’s at hundred’s place = 396
Sum of the digit’s at thousand’s place = 396
∴ Sum of all four digit numbers formed using the digits 0, 2, 5, 7, 8
= 396 × 10° + 396 × 10¹ + 396 × 10² + 396 × 10³
= 396 × ( 10° + 101 + 102 + 103)
= 396 × ( 1 + 10 + 100 + 1000)
= 396 × 1111 = 571956

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 4 Combinatorics and Mathematical Induction Ex 4.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.1

Question 1.
(i) A person went to a restaurant for dinner. In the menu card, the person saw 10 Indian and 7 Chinese food items. In how many ways the person can select either an Indian or Chinese food?
Answer:
Selecting an Indian food item from the given 10 can be done in 10 ways. Selecting a Chinese food item from the given 7 can be done in 7 ways.
∴ Selecting an Indian or Chinese food can be done in 10 + 7 = 17 ways.

(ii) There are 3 types of a toy car and 2 types of toy train are available in a shop. Find the number of ways a baby can buy a toy car and a toy train?
Answer:
Number of types of Toy car = 3
Number of types of Toy Train = 2
Number of ways of buying a Toy car = 3 ways
Number of ways of buying a toy train = 2 ways
∴ By fundamental principle of multiplication, number of ways of buying a toy car and a toy train = 3 × 2 ways = 6 ways

(iii) How many two – digit numbers can be formed using 1 , 2,3,4,5 without repetition of digits?
Answer:

The given digits are 1, 2, 3, 4, 5
A two-digit number has a unit place and 10’s place. We are given 5 digits (1, 2, 3, 4, 5). The unit place can be filled (using the 5 digits) in 5 ways. After filling the unit place since repetition is not allowed one number (filled in the unit place) should be excluded. So the 10’s place can be filled (using the remaining 4 digits) in 4 ways.
∴ Unit place and 10’s place together can be filled in 5 × 4 = 20 ways. So the number of two-digit numbers = 20

(iv) Three persons enter into a conference hall in which there are 10 seats. In how many ways can they take their seats?
Answer:
Number of seats in the conference hall = 10
Number of persons entering into the conference hall = 3
Number of ways of getting a seat for 1st person = 10
Number of ways of getting a seat for 2nd person = 9
Number of ways of getting a seat for 3rd person = 8
By fundamental principle of multiplication, number of ways of getting seats for 3 persons in conference hall = 10 × 9 × 8 ways = 720 ways

(v) In how ways 5 persons can be seated In a row?
Answer:
Number of persons = 5

5 persons can be arranged among themselves in 5! ways
(i.e) 5 × 4 × 3 × 2 × 1 = 120 ways

Question 2.
(i) A mobile phone has a passcode of 6 distinct digits. What is the maximum number of attempts one makes to retrieve the passcode?
Answer:
Number of distinct digit in a passcode of a mobile phone = 6

First digit can be tried in 10 ways using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Second digit can be tried in 9 ways
Third digit can be tried in 8 ways
Fourth digit can be tried in 7 ways
Fifth digit can be tried in 6 ways
Sixth digit can be tried in 5 ways
Therefore, the maximum number of attempts made to retrieve the passcode = 10 × 9 × 8 × 7 × 6 × 5 = 151200

(ii) Given four flags of different colours, how many different signals can be generated if each signal requires the use of three flags, one below the other?
Answer:

Number of flags = 4
Number of flags required for a signal = 3
The total number of signals is equal to the number of ways of filling 3 places in succession by 4 flags of different colours. Number of ways of filling the top place using 4 different colour flags is 4 ways. Number of ways of filling the middle place using the remaining 3 different colour flags is 3 ways. Number of ways of filling the bottom place using the remaining 2 different colour flags is 2 ways.

Therefore, by fundamental principle of multiplication, the total number of signals = 4 × 3 × 2 = 24 ways

Question 3.
Four children are running a race.
(i) In how many ways can the first two places be filled?
(ii) In how many different ways could they finish the race?
Answer:
(i) Number of children in the running race = 4
The first place can be filled in (from the 4 children) 4 ways
After filling in the first place only 3 children are left out
So the second place can be filled in (from the remaining 3 children) 3 ways
So the first and the second places together can be filled in 4 × 3 = 12 ways

(ii) The first and second places can be filled in 12 ways
The third-place can be filled (from the remaining 2 children) in 2 ways and the fourth place can be filled in 1 way
So the race can be finished in 12 × 2 × 1 = 24 ways

Question 4.
Count the number of three – digit numbers which can be formed from the digits 2, 4, 6, 8 if
(i) Repetitions of digits is allowed.
(ii) Repetitions of digits is not allowed?
Answer:
(i) Repetitions of digits is allowed
The given digits are 2, 4, 6, 8

A number of ways of filling the unit place using the 4 digits 2, 4, 6, 8 is 4 ways. Number of ways of filling the tens place using the 4 digits 2, 4, 6, 8 in 4 ways Number of ways of filling the hundred’s place using the 4 digits 2, 4, 6, 8 is 4 ways

Therefore, by fundamental principle of multiplication, the total number of 3 digit numbers = 4 × 4 × 4
= 64 ways

(ii) The unit place can be filled (using the 4 digits) in 4 ways after filling the unit place since repetition of digits is not allowed that digit should be excluded.
So the 10’s place can be filled in (4 – 1) 3 ways and the 100’s place can be filled in (3 – 1) 2 ways
So the unit place, 10’s and 100’s places together can be filled in 4 × 3 × 2 = 24 ways
(i.e) The number of 3 digit numbers = 4 × 3 × 2 = 24 ways

Question 5.
How many three-digit numbers are there with 3 in the unit place?
(i) with repetition
(ii) without repetition.
Answer:
(i) With repetition:

The given digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
The unit place can be filled in only one way using the digit 3. The ten’s place can be filled in 10 ways using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. The hundred’s place can be filled in 9 ways using the digits 1, 2, 3, 4, 5, 6, 7, 8, 9.

Therefore, by the fundamental principle of multiplication, the total number of 3 digit numbers is = 1 × 10 × 9 = 90

(ii) Without repetition:

The digits are 0, 1,2, 3, 4, 5, 6, 7, 8, 9
A three-digit number has 3 digits l’s, 10’s, and 100’s place.
The unit place is (filled by 3) filled in one way.
After filling the unit place since the digit ‘0’ is there, we have to fill the 100’s place. Now to fill the 100’s place we have 8 digits (excluding 0 and 3) So 100’s place can be filled in 8 ways.
Now to fill the 10’s place we have again 8 digits (excluding 3 and any one of the number) So 10’s place can be filled in 8 ways.
∴ Number of 3 digit numbers with ‘3’ in unit place = 8 × 8 × 1 = 64

Question 6.
How many numbers are there between 100 and 500 with the digits 0,1,2,3,4,5 if
(i) Repetition of digit is allowed
(ii) Repetition of digits is not allowed.
Answer:
(i) Repetition of digit is allowed:

The numbers between 100 and 500 will have 3 digits. The unit place can be filled in 6 ways using the digits 0, 1, 2, 3, 4, 5. The ten’s place can be filled in 6 ways using the digits 0, 1, 2, 3, 4, 5. The hundred’s place can be filled in 4 ways using the digits 0, 1, 2, 3, 4, 5 ( Excluding 0 and 5). Therefore, by fundamental principle of multiplication, the number of 3 digit, numbers between 100 and 500 with repetition of digits using the digits 0, 1, 2, 3, 4, 5 is = 6 × 6 × 4 = 144

(ii) Repetition of digits is not allowed:

The 100’s place can be filled (by using 1, 2, 3, 4) 10’s in 4 ways
The 10’s place can be filled in (6 – 1) 5 ways and the unit place can be filled in (5 – 1) 4 ways
So the number of 3 digit number 4 × 5 × 4 = 80

Question 7.
How many three-digit odd numbers can be formed by using the digits 0, 1, 2, 3, 4, 5? if
(i) The repetition of digits is not allowed
(ii) The repetition of digits is allowed.
Answer:
The given digits are 0, 1, 2, 3, 4, 5
To find the possible 3 – digit odd numbers.

(i) Repetition of digits is not allowed:

Since we need 3 – digit odd numbers the unit place can be filled in 3 ways using the digits 1, 3 or 5. Hundred’s place can be filled in 4 ways using the digits 0, 1, 2, 3, 4, 5 excluding 0 and the number placed in unit place. Ten’s place can be filled in 4 ways using the digits 0, 1, 2, 3, 4, 5 excluding the digit placed in the hundred’s place.

Therefore, by the fundamental principle of multiplication, the number of 3 – digit odd numbers formed without repetition of digits using the digits 0, 1, 2, 3, 4, 5 is
= 4 × 4 × 3 = 48

(ii) Repetition of digits is allowed:

The unit place can be filled in 3 ways. We are given 6 digits.
So 10’s place can be filled in 6 ways and the 100’s place can be filled in (6 – 1) (excluding zero) 5 ways
So the Number of 3 digit numbers = 3 × 6 × 5 = 90

Question 8.
Count the numbers between 999 and 10000 subject to the condition that there are
(i) no restriction
(ii) no digit is repeated
(iii) At atleast one of the digits is repeated.
Answer:
To find the numbers between 999 and 10,000 using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
To find the possible 4 digit numbers.

(i) No restriction:

Thousand’s place can be filled in 9 ways using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 excluding 0. Since there is no restriction, the hundred’s place, Ten’s place, and the unit place can be filled in 10 ways using the digit 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Therefore, by the fundamental principle of multiplication, the number of 4 digit numbers between 999 and 10,000 is = 9 × 10 × 10 × 10 = 9000

(ii) No digit is repeated:

Thousand’s place can be filled in 9 ways using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 excluding 0. Since repetition is not allowed. The unit place can be filled in 9 ways using the digits 0,1, 2, 3, 4, 5, 6, 7, 8, 9 excluding the digit placed in the thousand’s place. Since repetition of digits is not allowed, the ten’s place can be filled in 8 ways using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 excluding the digits used in thousand’s a place and unit place. Since repetition of digits is not allowed, the hundred’s place can be filled in 7 ways using the digits 0,1,2,3,4, 5,6,7,8,9 excluding the digits used in thousand’s a place and unit place.

Therefore, by the fundamental principle of multiplication, the number of numbers between 999 and 10,000 without repetition of digits is = 9 × 7 × 8 × 9 = 4536

(iii) At least one of the digits is repeated:
Required number of 4 digit numbers = Total number of 4 digit numbers – Number of 4 digit numbers when no digit is repeated = 9000 – 4536 = 4464

Question 9.
How many three-digit numbers, which are divisible by 5, can be formed using the digits 0, 1, 2, 3, 4, 5 if
(i) Repetition of digits is not allowed?
(ii) Repetition of digits is allowed?
Answer:
The given digits are 0, 1, 2, 3, 4, 5
To find the 3 – digit numbers formed by using the digits 0, 1, 2, 3, 4, 5 which are divisible by 5.

(i)The repetition of digits are not allowed:

Since the 3 – digit number is divisible by 5, the unit place can be filled in 2 ways using the digits 0 or 5

Case (i) When the unit place is filled with the digit 0. The hundreds place can be filled in 5 ways using the digits 1, 2, 3, 4, 5 and the ten’s place can be filled in 4 ways using the digits 0, 1, 2, 3, 4, 5 excluding 0 and the digit which is placed in hundred’s place.

Therefore, by fundamental principle of multiplication, the number of 3 – digit numbers divisible by 5 is
= 5 × 4 × 1 = 20

Case (ii) When the unit place is tilled with the digit 5, since repetition of digit is not allowed the hundred’s place can be filled in 4 ways using the digits 1, 2 , 3 , 4 (0 and 5 are excluded). The ten’s place can be filled in 4 ways using the digits 0, 1 , 2, 3 , 4, 5 (excluding 5 and the digit placed in the hundred’s place).
Therefore, by the fundamental principle of multiplication, the number of 3 – digit numbers, in this case, is = 4 × 4 × 1 = 16
Therefore, the total number of 3 – digit numbers divisible by 5 using the digits 0, 1, 2, 3, 4, 5 is = 20 + 16 = 36

(ii) The repetition of digits are allowed:

The digits are
0 1 2 3 4 5
To get a number divisible by 5 we should have the unit place as 5 or 0 So the unit place (using 0 or 5) can be filled in 2 ways.
The 10’s place can be filled (Using 0, 1, 2, 3, 4, 5) in 6 ways and the 100’s place (Using 1, 2, 3, 4, 5) can be filled in 5 ways.
So the number of 3 digit numbers ÷ by 5 (with repetition) = 2 × 6 × 5 = 60

Question 10.
To travel from place A to place B, there are two different bus routes B₁, B₂, two different train routes T₁, T_2, and one air route A₁. From place B to place C, there is one bus route say B’₁, two different train routes say T’₁, T’_2, and one air route A’₁. Find the number of routes of commuting from place A to place C via place B without using a similar mode of transportation.
Answer:
Route map diagram for the given data.

The possible choices for a number of routes commuting from A to place C via place B without using similar mode transportation are
(B₁, T’₁), (B₁, T’₂), ( B₁, A₁), ( B₂, T’₁), (B₂, T’₂)
(B₂, A’₁), (T₁, B’₁), (T₁, A’₁), ( T₂, B’₁), ( T₂, A’₁) (A₁, B’₁) , (A₁, T’₁) and (A₁, T’₂)
Therefore, the Required number of routes is 13.

Question 11.
How many numbers are there between 1 and 1000 (both inclusive) which are divisible neither by 2 nor by 5 ?
Answer:
From 1 to 1000, the numbers ÷ by 2 = 500
the number ÷ by 5 = 200
and the numbers ÷ by 10 = 100(5 × 2 = 10)
So number ÷ by 2 or 5 = 500 + 200 – 100 = 600
Total numbers from 1 to 1000 = 1000
So the number of numbers which are ÷ neither by 2 nor by 5 = 1000 – 600 = 400

Three-digit numbers:

The unit place can be filed in 4 ways using the digits 1, 3, 7, 9. Hundred’s place can be filled in 9 ways excluding 0. Ten’s place can be filled in 10 ways using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Therefore, the required number of 3 digit numbers neither divisible by 2 nor by 5 is = 9 × 10 × 4 = 360.
There is only one 4 – digit number, but it is divisible by 2 and 5.
Therefore, required numbers using fundamental principle of addition = 4 + 36 + 360 = 400

Question 12.
How many strings can be formed using the letters of the word LOTUS if the word
(i) either start with L or end with S?
(ii) neither starts with L nor ends with S?
Answer:
(i) Either starts with L or ends with S

The first box is filled with the letter L. The second box can be filled with the remaining letters O, T, U, S in 4 ways. The third box can be filled with the remaining letters excluding L and the letter placed in box 2 in 3 ways. The fourth box can be filled with the remaining letters excluding L and the letters placed in a box – 2 and box – 3 in 2 ways. The fifth box can be filled with the remaining one letter excluding L and the letters placed in a box – 2 and box – 3, box – 4 in 1 way.
Therefore, by fundamental principle of multiplication, the number of words start with L is = 1 × 4 × 3 × 2 × 1 = 24

Since the word ends with S, the fifth box can be filled in one way with the letter S. The remaining four boxes can be filled 4 × 3 × 2 × 1 way.
Therefore, the number of words ending with S = 4 × 3 × 2 × 1 × 1 = 24

Number of words starting with L and ends with S: The first box can be filled with L in one way fifth box can be filled with S in one way second box, third box, and fourth box can be filled in 3x2x1 ways with the remaining letters O, T, U.
∴ Number of words starting with L and ends with S = 1 × 3 × 2 × 1 × 1 = 6
Therefore, by fundamental principle of addition, number of words either starts with L or ends with S = 24 + 24 – 6 = 48 – 6 = 42

(ii) Neither starts with L nor ends with S Total number of words formed using the letters L, O, T, U, S is = 5 × 4 × 3 × 2 × 1 = 120
The number of words neither starts with L nor ends with S = Total number of words – Number of words starts with either L or ends with S = 120 – 42 = 78

Question 13.
(i) Count the total number of ways of answering 6 objective type questions, each question having 4 choices.
Answer:
Count the total number of ways of answering 6 objective type questions, each question having 4 choices.
One question can be answered in 4 ways
Two questions can be answered in 4 × 4 = 4² ways
∴ Six questions can be answered in 46 ways

(ii) In how many ways 10 pigeons can be placed in 3 different pigeon holes?
Solution:
First pigeons can be placed in a pigeon-hole in 3 ways (selecting 1 from 3 holes)
Second pigeons can be placed in a pigeon-hole in 3 ways Tenth pigeons can be placed in a pigeon-hole in 3 ways
So total number of ways in which all the number 10 place can be sent = 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 = 310 ways

(iii) Find the number of ways of distributing 12 distinct prizes to 10 students?
Solution:
To give the first prize we have to select, from the 10 students which can be done in 10 ways.
To give the second prize we have to select one from the 10 students which can be done is 10 ways.
To give the 12th prize we have to select one from 10 students which can be done in 10 ways.
So all the 12 prizes can be given in (10 × 10 × 10 …. 12 times) = 1012 ways.

Question 14.
Find the value of
(i) 6!
(ii) 4! +5!
(iii) 3! – 2!
(iv) 31 × 21
(v) \(\frac{12 !}{9 ! \times 3 !}\)
(vi) \(\frac{(n+3) !}{(n+1) !}\)
Answer:
(i) 6!
6! = 6 × 5 × 4 × 3 × 2 × 1 = 720

(ii) 4! +5!
4! +5! = (4 × 3 × 2 × 1) + (5 × 4 × 3 × 2 × 1)
= (4 × 3 × 2 × 1) [1 + 5]
= 24 × 6 = 144

(iii) 3! – 2!
3! – 2! = (3 × 2 × 1) × (4 × 3 × 2 × 1)
= 6 × 24 = 144

(iv) 3! × 2!
3! × 2! = (3 × 2 × 1) × (4 × 3 × 2 × 1)
= 6 × 24 = 144

(v) \(\frac{12 !}{9 ! \times 3 !}\)

= 2 × 11 × 10 = 220

(vi) \(\frac{(n+3) !}{(n+1) !}\)

= (n + 3) (n + 2)
= n² + 3n + 2n + 6
= n² + 5n + 6

Question 15.
Evaluate \(\frac{\mathbf{n} !}{\mathbf{r} !(\mathbf{n}-\mathbf{r}) !}\) when
(i) n = 6 , r = 2
(ii) n = 10, r = 3
(iii) For any n with r = 2.
Answer:
(i) n = 6 , r = 2

(ii) n = 10, r = 3

(iii) For any n with r = 2.

Question 16.
Find the value of n if
(i) ( n + 1) ! = 20 ( n – 1 )!
(ii) \(\frac{1}{8 !}+\frac{1}{9 !}=\frac{n}{10 !}\)
Answer:
(i) ( n + 1) ! = 20 ( n – 1 )!
(n + 1) n(n – 1)! = 20(n – 1)!
n(n + 1) = 20
n² + n – 20 = 0
n² + 5n – 4n – 20 = 0
n(n + 5) – 4(n + 5) = 0
(n – 4) (n + 5) = 0
n – 4 = 0 or n + 5 = 0
n = 4 or n = -5
But n = -5 is not possible. ∴ n = 4

(ii) \(\frac{1}{8 !}+\frac{1}{9 !}=\frac{n}{10 !}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 Trigonometry Ex 3.12 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.12

Choose the correct or the most suitable answer:

Question 1.

(1) √2
(2) √3
(3) 2
(4) 4
Answer:
(4) 4

Explaination:

Question 2.
If cos 28° + sin 28°= k³, then cos 17° is equal to
(1) \(\frac{\mathbf{k}^{3}}{\sqrt{2}}\)
(2) \(-\frac{\mathbf{k}^{3}}{\sqrt{2}}\)
(3) \(\pm \frac{\mathbf{k}^{3}}{\sqrt{2}}\)
(4) \(-\frac{\mathbf{k}^{3}}{\sqrt{3}}\)
Answer:
(1) \(\frac{\mathbf{k}^{3}}{\sqrt{2}}\)

Explaination:
cos 28° + sin 28° = k³
cos 28° + sin (90° – 62°) = k³
cos 28° + cos 62° = k³

2 cos 45° . cos 17° = k³
2 × \(\frac{1}{\sqrt{2}}\) cos 17° = k³
√2 cos 17° = k³
cos 17° = \(\frac{\mathrm{k}^{3}}{\sqrt{2}}\)

Question 3.
The maximum value of
4 sin²x + 3 cos²x + sin \(\) + cos \(\) is
(1) 4 + √2
(2) 3 + √2
(3) 9
(4) 4
Answer:
(1) 4 + √2

Explaination:
4 sin²x + 3 cos²x + sin \(\frac{x}{2}\) + cos \(\frac{x}{2}\)
= sin²x + 3 sin²x + 3 cos²x + sin \(\frac{x}{2}\) + cos \(\frac{x}{2}\)
= sin²x + 3(sin²x + cos²x) + sin \(\frac{x}{2}\) + cos \(\frac{x}{2}\)
= 3 + sin²x + sin \(\frac{x}{2}\) + cos \(\frac{x}{2}\) —– (1)
Maximum value of sin x = 1
sin x = 1 when x = \(\frac{\pi}{2}\)
Maximum value of sin²x = 1
Maximum value is obtained when x = \(\frac{\pi}{2}\)
∴ (1) ⇒ 4 sin² x + 3 cos² x + sin \(\frac{x}{2}\) + cos \(\frac{x}{2}\)
= 3 + 1 + sin \(\left(\frac{90^{\circ}}{2}\right)\) + cos \(\left(\frac{90^{\circ}}{2}\right)\)
= 4 + sin 5° + cos 45°
= 4 + \(\frac{1}{\sqrt{2}}\) + \(\frac{1}{\sqrt{2}}\) = 4 + \(\frac{2}{\sqrt{2}}\)
= 4 + √2

Question 4.

(1) \(\frac{1}{8}\)
(2) \(\frac{1}{2}\)
(3) \(\frac{1}{\sqrt{3}}\)
(4) \(\frac{1}{\sqrt{2}}\)
Answer:
(1) \(\frac{1}{8}\)

Explaination:

Question 5.
If π < 2θ < \(\frac{3 \pi}{2}\), \(\sqrt{2+\sqrt{2+2 \cos 4 \theta}}\) equals to
(1) – 2 cos θ
(2) – 2 sin θ
(3) 2 cos θ
(4) 2 sin θ
Answer:
(1) – 2 cos θ

Explaination:



∴ θ lies in the second quadrant, cos θ is negative in the II^nd quadrant.
∴ \(\sqrt{2+\sqrt{2+2 \cos 4 \theta}}\) = – 2 cos θ

Question 6.
If tan 40° = λ, then

(1) \(\frac{1-\lambda^{2}}{\lambda}\)
(2) \(\frac{1+\lambda^{2}}{\lambda}\)
(3) \(\frac{1+\lambda^{2}}{2 \lambda}\)
(4) \(\frac{1-\lambda^{2}}{2 \lambda}\)
Answer:
(4) \(\frac{1-\lambda^{2}}{2 \lambda}\)

Explaination:

Question 7.
cos 1° + cos 2° + cos 3° + ….. + cos 179° =
(1) 0
(2) 1
(3) – 1
(4) 89
Answer:
(1) 0

Explaination:
cos 1° + cos 2° + cos 3° + ……………… + cos 179°
= (cos 1° + cos 179°) + (cos 2° + cos 178°) + (cos 3° + cos 177°) + …………..

= 2 cos 90° cos 89° + 2 cos 90° . cos 88° + …………….
= 2 × 0 × cos 89°+ 2 × 0 × cos 88° + …………..
= 0

Question 8.
Let f_k(x) = \(\frac{1}{k}\)[sin^kx + cos^kx] where x ∈ R and k ≥ 1. Then f₄(x) – f₆(x) =
(1) \(\frac{1}{4}\)
(2) \(\frac{1}{12}\)
(3) \(\frac{1}{6}\)
(4) \(\frac{1}{3}\)
Answer:
(2) \(\frac{1}{12}\)

Explaination:

Question 9.
Which of the following is not true?
(1) sin θ = – \(\frac{3}{4}\)
(2) cos θ = – 1
(3) tan θ = 25
(4) sec θ = \(\frac{1}{4}\)
Answer:
(4) sec θ = \(\frac{1}{4}\)

Explaination:
We know |cos θ| < 1
sec θ = \(\frac{1}{4}\)
⇒ \(\frac{1}{\cos \theta}\) = \(\frac{1}{4}\)
⇒ cos θ = 4
which is not possible.

Question 10.
cos 2θ cos 2Φ + sin²(θ – Φ) – sin²(θ + Φ) is equal to
(1) sin 2 (θ + Φ)
(2) cos 2 (8 + Φ)
(3) sin 2 (θ – Φ)
(4) cos 2(θ – Φ)
Answer:
(2) cos 2 (8 + Φ)

Explaination:
cos 2θ cos 2Φ + sin²(θ – Φ) – sin²(θ + Φ)


= cos 2θ cos 2Φ – sin 2θ sin 2Φ
= cos(2θ + 2Φ)
= cos 2(θ + Φ)

Question 11.

(1) sin A + sin B + sin C
(2) 1
(3) 0
(4) cos A + cos B + cos C
Answer:
(3) 0

Explaination:

Question 12.
If cos pθ + cos qθ = o and if p ≠ q then θ is equal to(n is any integer)
(1)
(2)
(3)
(4)
Answer:
Given cos pθ + cos qθ = o

Question 13.
If tan α and tan β are the roots of x² + ax + b = 0 then \(\frac{\sin (\alpha+\beta)}{\sin \alpha \sin \beta}\) is equal to
(1) \(\frac{\mathbf{b}}{\mathbf{a}}\)
(2) \(\frac{\mathbf{a}}{\mathbf{b}}\)
(3) –\(\frac{\mathbf{a}}{\mathbf{b}}\)
(4) –\(\frac{\mathbf{b}}{\mathbf{a}}\)
Answer:
(3) –\(\frac{\mathbf{a}}{\mathbf{b}}\)

Explaination:
x² + ax + b = 0
Given tan α and tan β are the roots of the above equation. Then

Question 14.
In a triangle ABC, sin² A + sin² B + sin² C = 2 then the triangle is .
(1) equilateral triangle
(2) isosceles triangle
(3) right triangle
(4) scalene triangle
Answer:
(3) right triangle

Explaination:
On simplifying we get
sin² A + sin² B + sin² C = 2 + 2 cos A cos B cos C
= 2 (given)
⇒ cos A cos B cos C = 0
cos A (or) cos B (or) cos C = 0
⇒ A (or) B (or) C = π/2
⇒ ABC (is a right angled triangle).

Question 15.
If f(θ) = |sin θ| + |cos θ|, θ ∈ R then f(θ) is in the interval
(1) [0, 2]
(2) [1, √2]
(3) [1, 2]
(4) [0, 1]
Answer:
(2) [1, √2]

Explaination:

f(θ) = |sin θ| + |cos θ|
To find the point of intersection of the sine curve and cosine curve solving

Question 16.

(1) cos 2x
(2) cos x
(3) cos 3x
(4) 2 cos x
Answer:
(4) 2 cos x

Explaination:
Consider the numerator cos 6x + 6 cos 4x + 15 cos 2x + 10
cos 6x + 6 cos 4x + 15 cos 2x + 10 = cos 6x + cos 4x + 5 cos 4x + 5 cos 2x + 10 cos 2x + 10
= (cos 6x + cos 4x) + 5 (cos 4x + cos 2x) + 10(cos 2x + 1)

= 2 cos 5x cos x + 10 cos 3x . cos x + 20 cos²x
= 2 cos x (cos 5x + 5 cos 3x + 10 cos x)

= 2 cos x

Question 17.
The triangle of the maximum area with a constant perimeter of 12m
(1) is an equilateral triangle with a side of 4m
(2) is an isosceles triangle with sides 2m, 5m, 5m
(3) is a triangle with sides 3m, 4m, 5m
(4) does not exist.
Answer:
(1) is an equilateral triangle with a side of 4m

Explanation:
A triangle will have a max area (with a given perimeter) when it is an equilateral triangle.

Question 18.
A wheel is spinning at 2 radians/second. How many seconds will it take to make 10 complete rotations?
(1) 10 π seconds
(2) 20 π seconds
(3) 5 π seconds
(4) 15 π seconds
Answer:
(1) 10 π seconds

Explanation:
1 rotation makes 2π^c
Distance travelled in 1 second = 2 radians
So time taken to complete 10 rotations = 6 × 2π = 20 π^c
\(=\frac{20 \pi}{2}=10 \pi\) seconds

Question 19.
If sin α + cos α = b, then sin 2α is equal to
(1) b² – 1, if b ≤ √2
(2) b² – 1, if b > √2
(3) b² – 1, if b ≥ √2
(4) b² – 1, if b < √2
Answer:
(1) b² – 1, if b ≤ √2

Explaination:
sin α + cos α = b
(sin α + cos α)² = b²
sinv α + cos² α + 2 sin α cos α = b²
1 + sin 2α = b²
sin 2α = b² – 1
But – 1 ≤ sin 2α ≤ I
– 1 ≤ b² – 1 ≤ 1
b² – 1 ≤ 1 ⇒ b² ≤ 2
⇒ b ≤ √2
∴ sin 2α = b² – 1 if b ≤ √2

Question 20.
In an ∆ABC
(i) sin \(\frac{\mathbf{A}}{2}\) sin \(\frac{\mathbf{B}}{2}\) sin \(\frac{\mathbf{C}}{2}\) > 0
(ii) sin A sin B sin C > 0,then
(1) Both (i) and (ii) are true
(2) only (1) is true
(3) only (ii) Is true
(4) neither (i) nor (ii) is true
Answer:
(1) Both (i) and (ii) are true

Explaination:
When A + B + C = 180°

When A + B + C = 180° each angle will be lesser than 180°
So sin A, sin B, sin C > 0
⇒ sin A sin B sin C > 0
So both (i) and (ii) are true

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 Trigonometry Ex 3.11 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.11

Question 1.
Find the principal value of
(i) sin^-1 \(\)
(ii) Cos^-1 \(\)
(iii) cosec^-1 (- 1)
(iv) sec^-1 (- √2)
(v) tan^-1 (√3)
Answer:
(i) sin^-1 \(\frac{1}{\sqrt{2}}\)

(ii) Cos^-1 \(\frac{\sqrt{3}}{2}\)

(iii) cosec^-1 (- 1)

(iv) sec^-1 (- √2)

(v) tan^-1 (√3)

Question 2.
A man standing directly opposite to one side of a road of width x meter views a circular shaped traffic green signal of diameter ‘a’ meter on the other side of the road. The bottom of the green signal Is ‘b’ meter height from the horizontal level of viewer’s eye. If ‘a’ denotes the angle subtended by the diameter of the green signal at the viewer’s eye, then prove that

Answer:
Given Width of the Road = x meter
Diameter of the signal AB = a meter
Height of the signal from the eye level = b meter
In ∆ ADC, DC = x, AC = AB + BC = a + b

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 Trigonometry Ex 3.10 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.10

Question 1.
Determine whether the following measurements produce one triangle, two triangles or no triangle. ∠B = 88°, a = 23 , b = 2. Solve if solution exists.
Answer:
Using sine formula

= 23 × 0.999
= 22.99
which is not possible
∴ Solution of the given triangle does not exsit.

Question 2.
If the sides of a ∆ ABC are a = 4, b = 6 and C = 8, then show that 4 cos B + 3 cos C = 2.
Answer:
In ∆ ABC Given that a = 4, b = 6, c = 8
Using cosine formula

Question 3.
In a ∆ ABC, if a = √3 – 1, b = √3 + 1 and C = 60° find the other side and other two angles.
Answer:

In a ∆ ABC, Given
a = √3 – 1, b = √3 + 1
C = 60°
Using cosine formula a
C² = a² + b² – 2 ab cos C
= (√3 – 1)² + (√3 + 1)² – 2(√3 – 1) × (√3 + 1) cos 6o°
= 3 – 2√3 + 1 + 3 + 2√3 + 1 – 2 (3 – 1) × \(\frac { 1 }{ 2 }\)
c² = 8 – 2 = 6 ⇒ c = √6
Using sine formula

sin (45° – 30°) = sin 45° . cos 30° – cos 45° sin 30°

From equations (1) and (2), we have
sin A = sin 15° ⇒ A = 15°
In ∆ ABC, we have A + B + C = 180°
15° + B + 60° = 180°
B = 180°- 75°
B = 105°
∴ The required sides and angles are
c = √6, A = 15°, B = 105°

Question 4.
In any ∆ ABC, prove that the area

Answer:
Area of ∆ ABC is ∆ = \(\frac { 1 }{ 2 }\) bc = sin A
Using cosine formula

Question 5.
In a ∆ABC, if a = 12 cm, b = 8 cm and C = 30°, then show that its area is 24 sq.cm.
Answer:

In ∆ ABC Given
a = 12 cm ,
b = 8 cm,
C = 30°

Question 6.
In a ∆ABC, if a = 18 cm, b = 24 cm and c = 30 cm, then show that its area is 216 sq.cm.
Answer:
In a ∆ ABC, Given a = 18 cm, b = 24cm and c = 30 cm

Area of the triangle ABC

Question 7.
Two soldiers A and B in two different underground bunkers on a straighi road, spot an intruder at the top of a hill. The angle of elevation of the intruder from A and B to the ground level in the eastern direction are 30° and 45° respectively. If A and B stand 5km apart, find the distance of the intruder from B.
Answer:
Let A and B be the two positions of the soldiers.
AC – direction of the intruder seen from A.
BC – the direction of the intruder seen from B.
∠ BAC = 30° angle of elevation of the intruder from A.
∠ PBC = 45° angle of elevation of the intruder from B.

Distance between A and B = 5k.m.
In ∆ ABC, ∠ ABC = 180° – 45° = 135°
∠ BCA = 180° – ( 135° + 30°)
= 180° – 165° = 15°
Using sine formula

Question 8.
A researcher wants to determine the width of a pond from east to west, which cannot be done by actual measurement. From a point P, he finds the distance to the eastern-most point of the pond to be 8 km, while the distance to the westernmost point from P to be 6 km. If the angle between the two lines of sight is 60°, find the width of the pond.
Answer:

A – be the easternmost point on the pond and
B – be the westernmost point on the pond.
AB – Width of the pond
P – Point of observation.
The distance of A from P = 8 km
Distance of B from P = 6km
Angle between the directions PA and PB
∠APB = 60°
In ∆ PAB, using cosine formula
AB² = PA² + PB² – 2PA . PB . cos ∠APB
AB² = 8² + 6² – 2 × 8 × 6 . cos 60°
= 64 + 36 – 96 × \(\frac { 1 }{ 2 }\)
= 100 – 48 = 52
AB = \(\sqrt{52}\) = \(\sqrt{4 \times 13}\)
AB = 2\(\sqrt{13}\) k.m.
Width of the pond = 2\(\sqrt{13}\) k.m

Question 9.
Two Navy helicopters A and B are flying over the Bay of Bengal at saine altitude from sea level to search a missing boat. Pilots of both the helicopters sight the boat at the same time while they are apart 10km from each other. If the distance of the boat from A is 6 km and if the line segment AB subtends 60° at the boat, find the distance of the boat from B.
Answer:
A , B are the positions of the helicopter above the sea level.

Distance between A and B = 10 km
C – Position of the boat on the surface of sea.
AC, BC are the directions of the boat as seen from A and B respectively.
Distance of the boat C from A = 6 k.m
∠ ACB = 60°
Using cosine formula
AB² = BC² + AC² – 2 BC . AC cos ∠ACB
c² = a² + b² – 2 ab cos C
10² = a² + 6² – 2a × 6 cos 60°
100 = a² + 36 – 12a\(\left(\frac{1}{2}\right)\)
0 = a² + 36 – 6a – 100
a² – 6a – 64 = 0

Question 10.
A straight tunnel is to be made through a mountain. A surveyor observes the two extremities A and B of the tunnel to be built from a point P in front of the mountain. If AP = 3 km, BP = 5 km, and ∠APB = 120°, then find the length of the tunnel to be built.
Answer:

p² = a² + b² – 2ab cos P
p² = 9 + 25 – 30 Cos 120°
p² = 9 + 25 – 30 (-1/2) = 34 + 15 = 49
⇒ p = \(\sqrt{49}\) = 7 km

Question 11.
A farmer wants to purchase a triangular-shaped land with sides 120 feet and 60 feet and the angle included between these two sides is 60°. If the land costs Rs.500 per square feet, find the amount he needed to purchase the land. Also, find the perimeter of the land.
Answer:

Let ∆ ABC be the shape of the land.
Given AB = 120 ft, AC = 60ft
∠ BAC = 60°
Using cosine formula in ∆ ABC
BC² = AB² + AC² – 2AB . AC cos ¿BAC
BC² = 120² + 60² – 2 × 120 × 60 cos (60°)
= 14400 + 3600 – 14400 × \(\frac { 1 }{ 2 }\)
= 18000 – 7200
BC² = 10800 = 100 × 2 × 2 × 3 × 3 × 3
BC² = 10² × 2² × 3² × 3
BC = \(\sqrt{10^{2} \times 2^{2} \times 3^{2} \times 3}\)
BC = 10 × 2 × 3√3
BC = 60√3 k.m.
Perimeter of the Land = AB + BC + AC
= 120 + 60√3 + 60
= 180 + 60√3
= 60 (3 + √3) feet.
Area of ∆ ABC = \(\frac { 1 }{ 2 }\) × AB × AC × sin ∠ BAC
= \(\frac { 1 }{ 2 }\) × 60 × 120 sin 60°
= 30 × 120 × \(\frac{\sqrt{3}}{2}\)
= 30 × 60 × √3
= 1800 √3 sq. feet.
Cost of 1 sq. feet Rs. 500
∴ Cost of 800 √3 sq. feet = 800 √3 × 500 = 900000√3
Total amount needed = Rs. 900000√3
Perimeter of the land = 60(3 + √3)feet.

Question 12.
A fighter jet has to hit a small target by flying a horizontal distance. When the target is sighted, the pilot measures the angle of depression to be 30°. If after 100 km, the target has an angle of depression of 45°, how far is the target from the fighter jet at that instant?
Answer:

Let A be the position of the jet fighter observing the target at an angle of depression 30°.
Also, Let B be the position of the jet 100 k.m away horizontally from A observing the target at an angle of depression 45°.
In ∆ TAB, AB = 100 k.m
∠TAB = 30°
∠ABT = 180°- 45° = 135°
∠ATB = 180° – (135°+ 300) = 180° – 165° = 15°

Question 13.
A plane is 1 km from one landmark and 2 km from another. From the plane’s point of view, the land between them subtends an angle of 45°. How far apart are the landmarks?
Answer:
A, B are the two landmarks,
C – Position of the plane.
The distance of the plane from the landmark A = 1 k.m
The distance of the plane from the landmark B = 2 k.m
∠ACB = 45°

From the ∆ ABC, using cosine formula
AB² = AC² + BC² – 2AC. BC. cos45°
= 1² + 2² – 2 × 1 × 2
AB² = 1 + 4 – 2 × √2 = 5 – 2√2
AB = \(\sqrt{5-2 \sqrt{2}}\)
Distance between the landmarks AB = \(\sqrt{5-2 \sqrt{2}}\) km.

Question 14.
A man starts his morning walk at a point A reaches two points B and C and finally back to A such that ∠A = 60° and ∠B = 45°, AC = 4km in the ∆ ABC. Find the total distance he covered during his morning walk.
Answer:

Given In ∆ABC
AC = 4 k.m
∠A = 60°,
∠B = 45°
∠C = 180° – (60° + 45°)
∴ ∠C = 180° – 105° = 75°
Using sine formula

Question 15.
Two vehicles leave the same place P at the same time moving along two different roads. One vehicle moves at an average speed of 60 km/hr and the other vehicle moves at an average speed of 80 km/hr. After half an hour the vehicle reaches destinations A and B. If AB subtends 60° at the initial point P, then find AB.
Answer:

P – Initial point.
PA – The direction of the first vehicle travels with speed km/hr.
PB – The direction of the second vehicle travels with a speed of 80km/hr.
Given in half an hour first vehicle reaches destination A.
∴ PA = \(\frac{60}{2}\) = 30 km.
Also in half an hour the second vehicle reaches the destination B.
∴ PA = \(\frac{80}{2}\) = km.
In ∆ PAB, PA = 30, PB = 40, ∠APB = 60°
Using cosine formula
AB² = PA² + PB² – 2PA PB cos ∠APB
AB = 30² + 40² – 2 × 30 × 40 cos 60°
= 900 + 1600 – 2400 × \(\frac { 1 }{ 2 }\)
= 2500 – 1200
AB² = 1300
AB = \(\sqrt{1300}\) = \(\sqrt{13 \times 100}\)
AB = 10√13 k.m.

Question 16.
Suppose that a satellite in space, an earth station, and the centre of earth all lie in the same plane. Let r be the radius of earth and R he the distance from the centre of earth to the satellite. Let d be the distance from the earth station to the satellite. Let 30° be the angle of elevation from the earth station to the satellite, If the line segment connecting the earth station and satellite subtends angle α at the centre of earth then prove that

Answer:

O – Centre of Earth,
A – Position of Earth station.
S – Position of the satellite.
Given the radius of Earth
OA = r
The angle of elevation of the satellite from the Earth station = 30°
The distance of the satellite from the Earth station AS = d
The distance of the satellite from the centre of the Earth OS = R.
Angle subtended by the line segment AS at the centre of earth ∠AOS = α
In △ AOS, OA = r, AS = d, OS = R, ∠AOS = α
Using cosine formula
AS² = OA² + OS² – 2 OA . OS cos ∠AOS
d² = r² + R² – 2(r) (R) cos α

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 Trigonometry Ex 3.9 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.9

Question 1.
In a ∆ ABC, if \(\frac{\sin A}{\sin C}=\frac{\sin (A-B)}{\sin (B-C)}\) prove that a², b², C² are in Arithmetic progression.
Answer:
\(\frac{\sin A}{\sin C}=\frac{\sin (A-B)}{\sin (B-C)}\)
sin A . sin (B – C) = sin C . sin (A – B)
sin (180° – (B + C)) . sin (B – C) = sin (180° – (A + B)) . sin (A – B)
sin (B + C) sin (B – C) = sin (A + B) sin (A – B) ——— (1)
sin(B + C) . sin(B – C) = (sin B cos C + cos B sin C) × (sin B cos C – cos B sin C)
= (sin B cos C)² – (cos B sin C)²
= sin² B cos² C – cos² B sin² C
= sin² B (1 – sin² C) – (1 – sin² B) sin² C
= sin² B – sin² B sin² C – sin² C + sin² B sin² C
sin ( B + C) . sin ( B – C) = sin² B – sin² C
Similarly,
sin (A + B ) . sin (A – B) = sin² A – sin² B
(1) ⇒ sin² B – sin² C = sin² A – sin² B
sin² B + sin² B = sin² A + sin² C
2 sin² B = sin² A + sin² C ——— (2)

Question 2.
The angles of a triangle A B C, are in Arithmetic Progression and if b : c = √3 : √2 find ∠A.
Answer:
Given that the angles A, B, C are in A. P.
∴ 2B = A + C
Also A + B + C = 180°
B + (A + C) = 180°
B + 2B = 180°
3B = 180° ⇒ B = 60°
A + C = 2B = 2 × 60° = 120°

A + 45° = 120°
A = 120° – 45° = 75°
A = 75°

Question 3.
In a ∆ ABC, if cos c = \(\frac{\sin \mathbf{A}}{2 \sin B}\) show that the triangle is isosceles.
Answer:

a² + b² – c² = a²
b² – c² = 0
b² = c² ⇒ b = c
Two sides of is ∆ ABC are equal.
∴ ∆ ABC is an isosceles triangle.

Question 4.
In a ∆ ABC, prove that

Answer:

Question 5.
In an ∆ABC, prove that a cos A + b cos B + c cos C = 2a sin B sin C.
Answer:
LHS = a cos A+ 6 cos B + c cos C
Using sine formula, we get k sin A cos A + k sin B cos B + k sin C cos C k
= \(\frac{k}{2}\) [2 sin A cos A + 2 sin B cos B + 2 sin C cos C]
= \(\frac{k}{2}\) [sin 2A + sin 2B + sin 2C]
= \(\frac{k}{2}\) [2 sin (A + B) . cos (A – B) + 2 sin C . cos C]
= \(\frac{k}{2}\) [2 sin (A – B) . cos (A – B) + 2 sin C . cos C]
= \(\frac{k}{2}\) [2 sin C . cos (A – B) + 2 sin C . cos C]
= k sin C [cos(A – B) + cos C]

= k sin C [cos (A – B) – cos (A + B)]
= k sin C . 2 sin A sin B
= 2k sin A . sin B sin C
= 2a sin B sin C
= RHS

Question 6.
In a ∆ ABC, ∠A = 60°. Prove that b + c = 2a cos \(\left(\frac{\mathbf{B}-\mathbf{C}}{2}\right)\)
Answer:
Given ∠A = 60°
A + B + C = 180°
60° + B + C = 180°
B + C = 180° – 60° = 120°

Question 7.
In an ∆ ABC, prove the following,
(i) a sin \(\left(\frac{\mathbf{A}}{2}+\mathbf{B}\right)\) = (b + c) . sin \(\frac{\mathbf{A}}{2}\)
Answer:

(ii) a (cos B + cos C) = 2(b + c) sin²\(\frac{\mathbf{A}}{2}\)
Answer:

(iii)
Answer:

(iv)
Answer:

(v)
Answer:

Question 8.
In a triangle ∆ ABC, prove that
(a² – b² + c²) tan B = (a² + b² – c²) tan C
Answer:

Question 9.
An Engineer has to develop a triangular shaped park with a perimeter 120m in a village. The park to be developed must be of maximum area. Find out the dimensions of the park.
Answer:
Let ∆ A B C be the triangular-shaped park.
a, b, c be the length of the sides.
Given perimeter of the park = 120 m
2s = a + b + c = 120m —– (1)
For a fixed perimeter 2s. the area of a triangle is maximum when a = b = c.
(1) = a + a + a = 120
3a = 120
⇒ a = 40m
Length of the sides 40 m, 40 m, 40 rn.

Question 10.
A rope of length 42m is given. Find the largest area of the triangle formed by this rope and find the dimensions of the triangle so formed.
Answer:
Let a, b, c be the lengths of the sides of the triangle.
Given the perimeter of the triangle
2s = a + b + c = 42m —-—(1)
For a fixed perimeter 2 s, the area of a triangle is maximum
when a = b = c.
(1) ⇒ a + a + a = 42
3a = 42 ⇒ a = \(\frac{42}{3}\)
a = 14m
∴ a = b = c = 14m

∴ The dimensions of the triangle are 14 m, 14 m, 14 m.
Maximum area = 49√3 sq.m.

Question 11.
Derive Projection formula from
(i) Law of sines,
(ii) Law of cosines.
Answer:
To prove (a) a = b cos C + c cos B
(b) b = c cos A + a cos C
(c) c = a cos B + b cos A

(i) Using the Law of sines,

(a) b cos C + c cos B = 2 R sin B cos C + 2 R sin C cos B
= 2 R ( sin B cos C + cos B sin C)
= 2R sin (B + C)
= 2R sin (180° – A)
b cos C + c cos B = 2R sin A = a
a = b cos C + c cos B

(b) c cos A + a cos C = 2R sin C cos A + 2R sin A cos C
= 2R (sin C cos A + cos C sin A)
= 2R sin(C + A)
= 2R sin(180° – B)
= 2R sin B = b
∴ b = c cos A + a cos C

(c) a cos B + b cosA = 2R sin A cos B + 2R sin B cos A
= 2R (sin A cos B + cos A sin B)
= 2R sin (A + B)
= 2R sin (180° – C)
= 2R sin C = c
∴ c = a cos B + b cos A

(ii) Using Law of cosines.