Category: Class 11

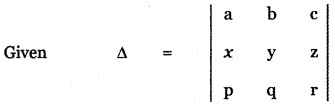
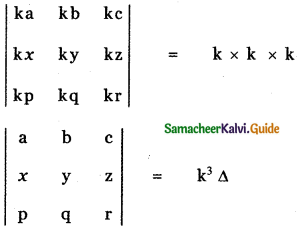
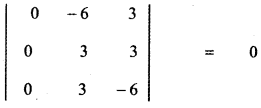
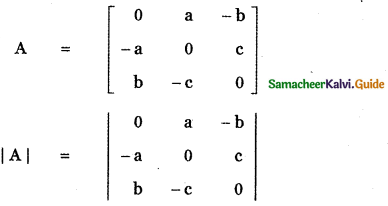
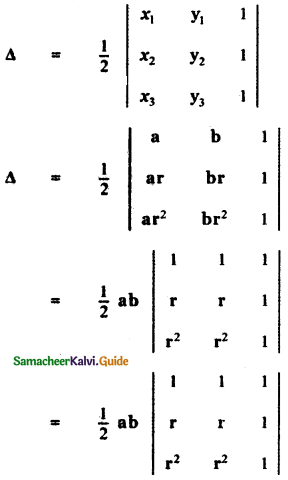
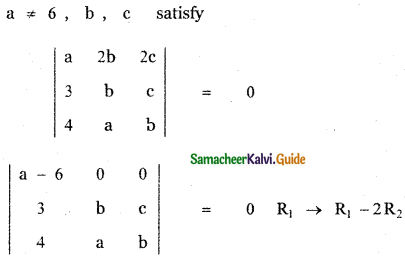
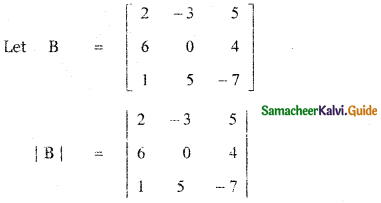
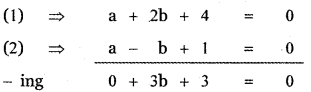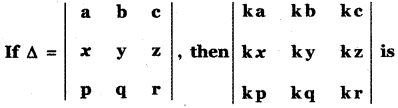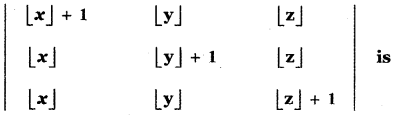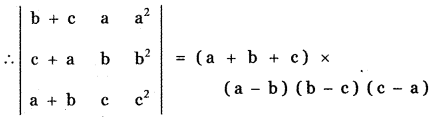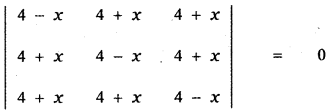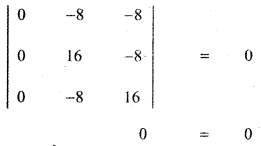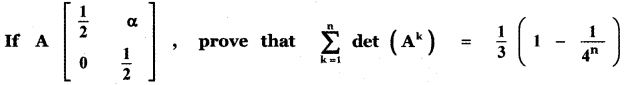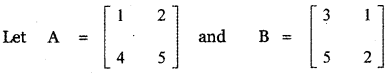Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 8 Vector Algebra – I Ex 8.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.2

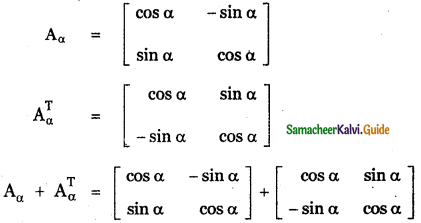
Question 1.
Verify whether the following ratios are direction cosines of some vector or not.
(i) \(\frac{1}{5}, \frac{3}{5}, \frac{4}{5}\)
(ii) \(\frac{1}{\sqrt{2}}, \frac{1}{2}, \frac{1}{2}\)
(iii) \(\frac{4}{3}, 0, \frac{3}{4}\)
Answer:
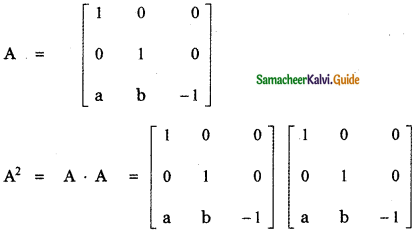
(i) \(\frac{1}{5}, \frac{3}{5}, \frac{4}{5}\)


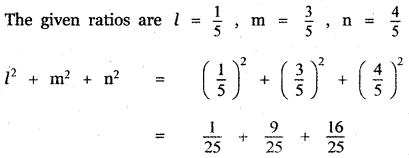
[If l, m, n are direction cosines of a vector then l² + m² + n² = 1]
∴ The given ratio \(\frac{1}{5}, \quad \frac{3}{5}, \quad \frac{4}{5}\) do not form the direction cosines of a vector.

(ii) \(\frac{1}{\sqrt{2}}, \frac{1}{2}, \frac{1}{2}\)

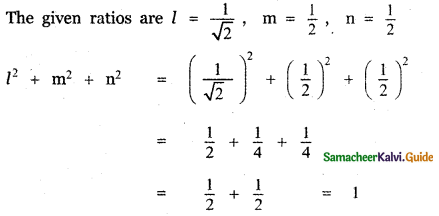
[If l, m, n are direction cosines of a vector then l² + m² + n² = 1]
∴ The given ratio form the direction cosines of a vector.

(iii) \(\frac{4}{3}, 0, \frac{3}{4}\)

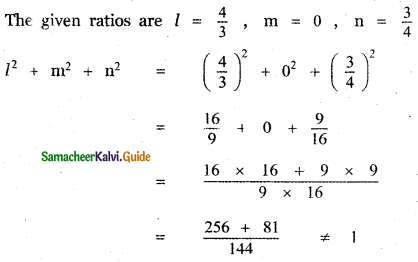
[If l, m, n are direction cosines of a vector then l² + m² + n² = 1]
∴ The given ratio do not form the direction cosines of a vector.

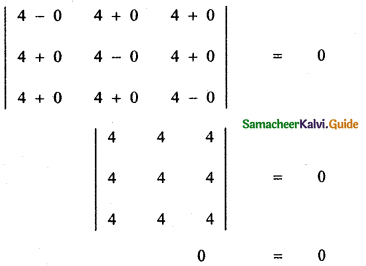
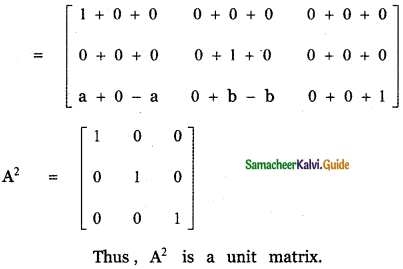
Question 2.
Find the direction cosines of a vector whose direction ratios are
(i) 1, 2, 3
(ii) 3, -1 , 3
(iii) 0, 0, 7
Answer:
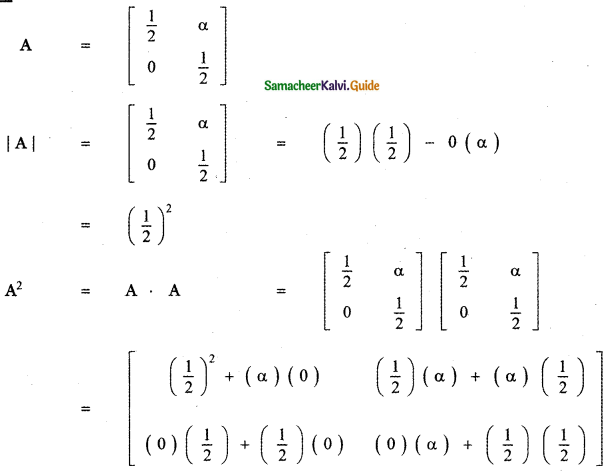
(i) 1, 2, 3
The given direction ratios are a = 1, b = 2 , c = 3

(ii) 3, – 1, 3
The given direction ratios are a = 3, b = – 1 , c = 3

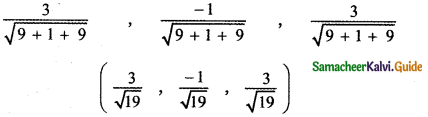
(iii) 0, 0, 7
The given direction ratios are a = 0, b = 0, c = 7

Question 3.
Find the direction cosines and direction ratios for the following vectors.
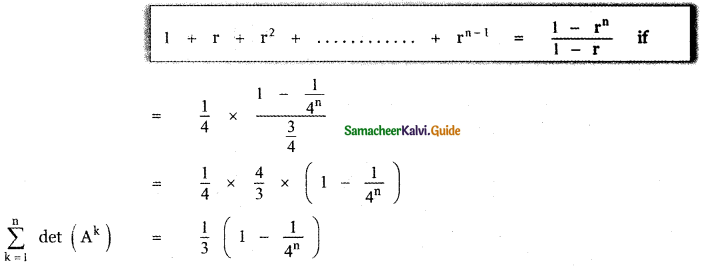
(i) 3î – 4ĵ + 8k̂
Answer:

(ii) 3î + ĵ + k̂
Answer:

(iii) ĵ
Answer:
ĵ = 0î + ĵ + 0k̂
The direction ratios of the vector ĵ are (0, 1, 0)
The direction cosines of the vector ĵ are

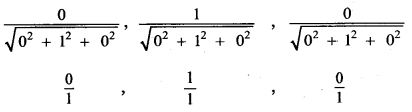
(0, 1, 0)
Direction ratios = (0, 1, 0)
Direction cosines = (0, 1, 0)

(iv) 5î – 3ĵ – 48k̂
Answer:

(v) 3î – 3k̂ + 4ĵ
Answer:

(vi) î – k̂
Answer:

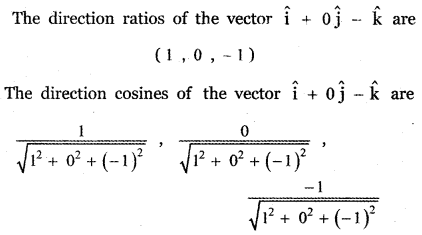
Question 4.
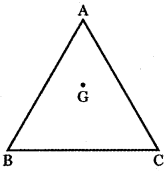
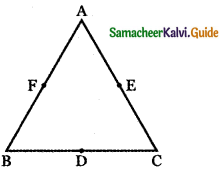
A triangle is formed by joining the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). Find the direction cosines of the medians.
Answer:
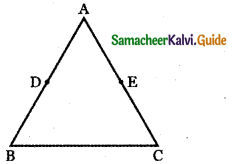
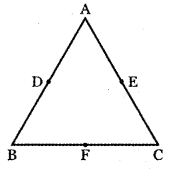
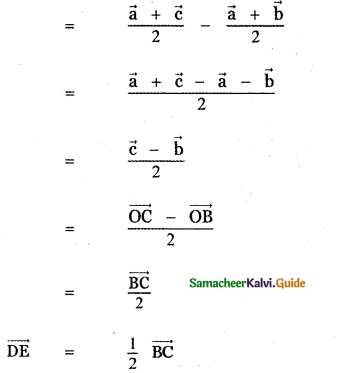
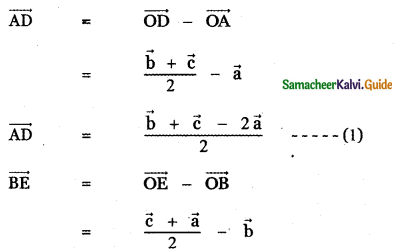
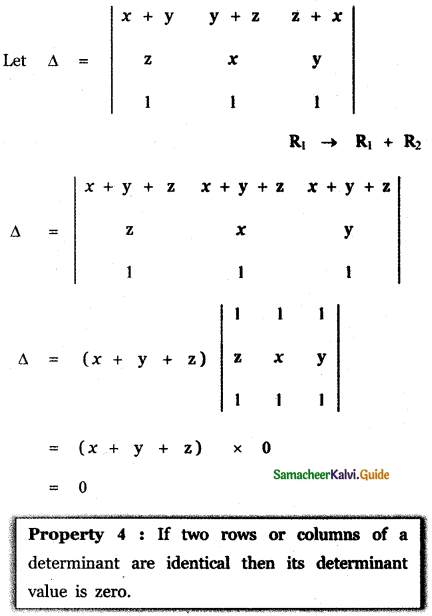
Let ABC be the triangle and D, E, F is the midpoints of the sides BC, CA, AB respectively. Then AD, BE, CF are the medians of ∆ ABC.
Given that the vertices of the triangle are A (1, 0, 0) , B (0, 1, 0 ) and C (0, 0, 1).

Question 5.
If \(\frac{1}{2}, \frac{1}{\sqrt{2}}\), a are the direction cosines of some vector, then find a.
Answer:
Given \(\frac{1}{2}, \frac{1}{\sqrt{2}}\), a are the direction cosines of some vector, then


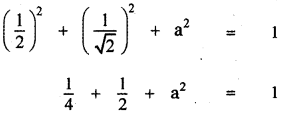
[If l, m, n are direction cosines of a vector then l² + m² + n² = 1]

Question 6.
If (a, a + b , a + b + c)is one set of direction ratios of the line joining (1, 0, 0) and (0, 1, 0), then find a set of values of a, b, c.
Answer:
Let A be the point (1, 0, 0) and B be the point (0, 1, 0) (i.e.,) \(\overrightarrow{\mathrm{OA}}=\hat{i}\) and \(\overrightarrow{\mathrm{OB}}=\hat{j}\)
Then \(\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}=\hat{j}-\hat{i}=-\hat{i}+\hat{j}\)
= (-1, 1, 0)
= (a, a + b, a + b + c)
⇒ a = -1, a + b = 1 and a + b + c = 0
Now a = -1 ⇒ -1 + b = 1 ;a + b + c = 0
⇒ b = 2; -1 + 2 + c = 0 ⇒ c + 1 = 0
⇒ c = -1
∴ a = -1; b = 2; c = -1.
Note: If we taken \(\overrightarrow{\mathrm{BA}}\) then we get a = 1, b = -2 and c = 1.

Question 7.
Show that the vectors 2î – ĵ + k̂ , 3î – 4ĵ – 4k̂, î – 3ĵ – 5k̂ form a right angled triangle.
Answer:

Question 8.
Find the value of λ for which the vector \(\vec{a}\) = 3î + 2ĵ + 9k̂ and \(\vec{b}\) = î + λĵ + 3k̂ are parallel.
Answer:

Question 9.
Show that the following vectors are coplanar
(i) î – 2ĵ + 3k̂, – 2î + 3ĵ – 4k̂, – ĵ + 2k̂
Answer:

(ii) 5î + 6ĵ + 7k̂, 7î – 8ĵ + 9k̂, 3î + 20ĵ + 5k̂
Answer:

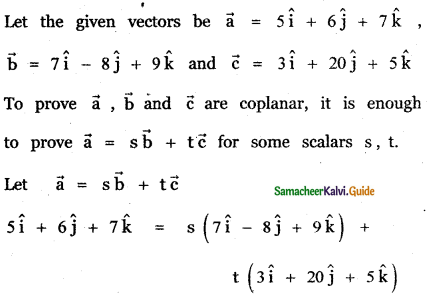
Question 10.
Show that the points whose position vectors 4î + 5ĵ + k̂, – ĵ – k̂, 3î + 9ĵ + 4k̂ and -4î + 4ĵ + 4k̂ are coplanar.
Answer:
Let the given position vectors of the points A, B, C, D be


Equating the like terms on both sides
-4 = 3s – 7t ………… (1)
-6 = 10s – 5t ……….. (2)
-2 = 5s …………. (3)
(3) ⇒ s = \(-\frac{2}{5}\)
Substituting in equation (2) , we have
-6 = 10 × \(-\frac{2}{5}\) – 5t
-6 = -4 – 5t
-6 + 4 = -5t
⇒ -5t = -2
⇒ t = \(\frac{2}{5}\)
Substituting for s and t in equation (1), we have

Question 11.
If \(\vec{a}\) = 2î + 3ĵ – 4k̂ , \(\vec{b}\) = 3î – 4ĵ – 5k̂ and \(\vec{c}\) = – 3î + 2ĵ + 3k̂ , find the magnitude and direction cosines of
(i) \(\vec{a}\) + \(\vec{b}\) + \(\vec{c}\)
(ii) 3\(\vec{a}\) – 2\(\vec{b}\) + 5\(\vec{c}\)
Answer:
The given vectors are \(\vec{a}\) = 2î + 3ĵ – 4k̂ , \(\vec{b}\) = 3î – 4ĵ – 5k̂ \(\vec{c}\) = – 3î + 2ĵ + 3k̂
(i) \(\vec{a}\) + \(\vec{b}\) + \(\vec{c}\)

(ii) 3\(\vec{a}\) – 2\(\vec{b}\) + 5\(\vec{c}\)

Question 12.
The position vectors of the vertices of a triangle are î + 2ĵ + 3k̂ ; 3î – 4ĵ + 5k̂ and – 2î + 3ĵ – 7k̂. Find the perimeter of the triangle.
Answer:
Let A, B, C be the vertices of a triangle ABC.
Given the position vectors of the vertices A, B, C are given by


∴ The required perimeter of the triangle ABC is given by AB + BC + AC = \(\sqrt{44}+\sqrt{218}+\sqrt{110}\)

Question 13.
Find the unit vector parallel to

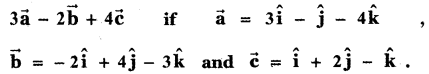
Answer:

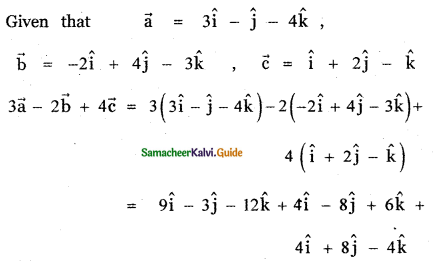
Question 14.
The position vectors \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) of three points satisfy the relation 2 \(\vec{a}\) + 7\(\vec{b}\) + 5\(\vec{c}\) = \(\vec{0}\). Are these points collinear?
Answer:

Question 15.
The position vector of the points P, Q, R, S are î + ĵ + k̂, 2î + 5ĵ, 3î + 2ĵ – 3k̂ and î – 6ĵ – k̂ respectively. Prove that the line and PQ and RS are parallel.
Answer:
Given that the position vector of the given points P, Q, R, S are

Question 16.
Find the value or values of m for which m (î + ĵ + k̂) is a unit vector.
Answer:
The given vector is m (î + ĵ + k̂)
Given that it is a unit vector.
∴ |m (i + j + k)| = 1
|m (i + j + k)| = 1
m (± \(\sqrt{1^{2}+1^{2}+1^{2}}\)) = 1
m = ± \(\frac{1}{\sqrt{3}}\)

Question 17.
Show that points A (1, 1, 1), B (1, 2, 3), and C (2, -1, 1 ) are vertices of an isosceles triangle.
Answer:
The given vertices of a triangle are
A(1, 1, 1) ,B(1 , 2, 3) and C (2, – 1, 1)
Position vector of A is \(\overrightarrow{\mathrm{OA}}\) = î + ĵ + k̂
Position vector of B is \(\overrightarrow{\mathrm{OB}}\) = î + 2ĵ + 3k̂
Position vector of C is \(\overrightarrow{\mathrm{OC}}\) = 2î – ĵ + k̂


∴ A, B, C are not collinear.
Hence A, B, C form a triangle.
AB = CA = √5
∴ ∆ABC is an isosceles triangle.

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 8 Vector Algebra – I Ex 8.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.1

Question 1.
Represent graphically the displacement of
(i) 45cm, 30° north of east
(ii) 80 km, 60° south of west
Answer:
(i) 45cm, 30° north of east

(ii) 80 km, 60° south of west

Question 2.
Prove that the relation R defined on the set V of all vectors by ‘\(\vec{a}\) R \(\vec{b}\) if \(\vec{a}\) = \(\vec{b}\)’ is an equivalence relation on V.
Answer:

Question 3.
Let \(\vec{a}\) and \(\vec{b}\) be the position vectors of the points A and B. Prove that the position vectors of the points which trisects the line segment AB are \(\frac{\overrightarrow{\mathbf{a}}+2 \overrightarrow{\mathbf{b}}}{3}\) and \(\frac{\overrightarrow{\mathbf{b}}+2 \overrightarrow{\mathbf{a}}}{3}\).
Answer:

Question 4.
If D and E are the midpoints of the sides AB and AC of a triangle ABC, prove that \(\overrightarrow{\mathbf{B E}}\) and \(\overrightarrow{\mathbf{D C}}\) = \(\frac{3}{2} \overrightarrow{\mathrm{BC}}\)
Answer:

Question 5.
Prove that the line segment joining the midpoints of two sides of a triangle is parallel to the third side whose length is half of the length of the third side.
Answer:
ABC be the triangle and D, E, F is the midpoints of the sides AB, BC, and AC respectively.
Let O be the origin and let \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) are the position vectors of the points A, B and C respectively.

∴ \(\overrightarrow{\mathbf{D E}}\) is parallel to \(\overrightarrow{\mathbf{B C}}\) and length of DE is half the length of BC. Similarly we can prove \(\overrightarrow{\mathbf{E F}}\) = \(\frac{1}{2} \overrightarrow{\mathrm{AB}} \cdot \overrightarrow{\mathrm{EF}}\)
parallel to \(\overrightarrow{\mathbf{A B}}\) and length of E is half the length of AB.
Also \(\overrightarrow{\mathbf{D F}}\) = \(\frac{1}{2} \overrightarrow{\mathrm{AC}}\)

\(\overrightarrow{\mathbf{D F}}\) is parallel to \(\overrightarrow{\mathbf{A C}}\) and length of DF is half the length of AC . Thus, the line segment joining the mid points of two sides of a triangle is parallel to the third side whose length is half of the length of the third side.

Question 6.
Prove that the line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram.
Answer:
Let ABCD be any quadrilateral D, E, F, G are the midpoints of the sides AB, BC, CD, AD respectively.





∴ EF and DG are parallel and equal.
∴ In the quadrilateral, DEFG’s opposite sides are parallel and equal. Therefore, DEFG is a parallelogram.

Question 7.
If \(\vec{a}\) and \(\vec{b}\) represent a side and a diagonal of a parallelogram , find the other sides and the other diagonal.
Answer:

Let ABCD be a parallelogram
Let \(\overrightarrow{\mathbf{A B}}\) = \(\vec{a}\)
\(\overrightarrow{\mathbf{A C}}\) = \(\vec{b}\)
Since ABCD is a parallelogram , we have

Question 8.
If \(\overline{\mathbf{P O}}+\overline{\mathbf{O Q}}\) = \(\overline{\mathbf{Q O}}+\overline{\mathbf{O R}}\), prove that the points P , Q , R are collinear.
Answer:

Let P, Q , R be the given points . Let O be the origin. Then the position vectors of
P, Q, R are \(\overrightarrow{\mathrm{OP}}\), \(\overrightarrow{\mathrm{OQ}}\) and \(\overrightarrow{\mathrm{OR}}\).

∴ P, Q, R lie on a straight line.
Hence, P, Q, R are collinear.

Question 9.
If D is the midpoint of the aide BC of i triangle ABC , prove that \(\overrightarrow{\mathbf{A B}}\) + \(\overrightarrow{\mathbf{A C}}\) = 2 \(\overrightarrow{\mathbf{A D}}\)
Answer:
Given D is the mid point of the side BC of a triangle ABC

Question 10.
If G is the centroid of a triangle ABC, prove that \(\overrightarrow{\mathbf{G A}}+\overrightarrow{\mathbf{G B}}+\overrightarrow{\mathbf{G C}}=\overrightarrow{\mathbf{0}}\)
Answer:

Let ABC be the triangle with centroid G. Let \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) be the position vectors of the vertices A, B and C respectively with respect to the origin O. Then

Question 11.
Let A, B, and C be the vertices of a triangle. Let D, E, and F be the midpoints of the sides BC, CA, and AB respectively. Show that \(\overrightarrow{\mathbf{A D}}+\overrightarrow{\mathbf{B E}}+\overrightarrow{\mathbf{C F}}=\overrightarrow{\mathbf{0}}\)
Answer:

Let ABC be the triangle. D, E, F are the mid points of the sides BC , CA , AB respectively . Let \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) be the position vectors of the vertices A, B, C respectively. Then

Question 12.
If ABCD is a quadrilateral and E and F are the midpoints of AC and BD respectively, then Prove that \(\overrightarrow{\mathbf{A B}}+\overrightarrow{\mathbf{A D}}+\overrightarrow{\mathbf{C B}}+\overrightarrow{\mathbf{C D}}=4 \overrightarrow{\mathbf{E F}}\)
Answer:

Given that ABCD is a quadrilateral. E and F are the midpoints of AC and BD.

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 7 Matrices and Determinants Ex 7.5 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.5

Choose the correct or the most suitable answer from the given four alternatives.

Question 1.
If a_ij = \(\) (3i – 2j) and A = [a_ij]_{3 × 2} is
(1)
(2)
(3)
(4)
Answer:
(2)

Explaination:

Question 2.
What must be the matrix X, if

(1)
(2)
(3)
(4)
Answer:
(1)

Explaination:

Question 3.
Which one of the following is not true about the matrix \(\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix} \right] \) ?.
(1) a scalar matrix
(2) a diagonal matrix
(3) an upper triangular matrix
(4) a lower triangular matrix
Answer:
(1) a scalar matrix

Explaination:
Let A = \(\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix} \right] \)
(1) a scalar matrix – not true
(2) a diagonal matrix – true
(3) an upper triangular matrix – true
(4) a lower triangular matrix – true

[(1) A square matrix A = [a_ij]_{m × n} is called a diagonal matrix if a_ij = 0 whenever i ≠ j
(2) A diagonal matrix whose entries along the principle diagonal are equal is called a scalar matrix.
(3) A square matrix is said to be an upper triangular matrix if all the elements below the main diagonal are zero.
(4) A square matrix is said to be a lower triangular matrix if all the elements above the main diagonal are zero.]

Question 4.
If A and B are two matrices such that A + B and AB are both defined, then
(1) A and B are two matrices not necessarily of same order
(2) A and B are square matrices of same order
(3) Number of columns of A is equal to the number of rows of B
(4) A = B
Answer:
(2) A and B are square matrices of same order

Explaination:
Given A and B are two matrices such that A + B and AB are both defined.
A + B defined means A and B are same order.
AB defined means , Number of columns of A equal to Number of rows of B.
A + B and AB are simultaneously defined.
Therefore A and B are of same order.

Question 5.
If A = \(\left[ \begin{matrix} λ & 1 \\ -1 & -λ \end{matrix} \right] \), then for what value of λ, A² = 0 ?
(1) 0
(2) ± 1
(3) – 1
(4) 1
Answer:
(2) ± 1

Explaination:

Question 6.
If A = \(\left[ \begin{matrix} 1 & -1 \\ 2 & -1 \end{matrix} \right]\), B = \(\left[ \begin{matrix} a & 1 \\ b & -1 \end{matrix} \right]\) and (A + B)² = A² + B², then the values of a and b are
(1) a = 4, b = 1
(2) a = 1, b = 4
(3) a = 0, b = 4
(4) a = 2, b = 4
Answer:
(2) a = 1, b = 4

Explaination:




L .2
Equating the like entrices
(a – 1)² = a² + b – 1 ………. (3)
o = a – 1 ………. (4)
2a+ 2 + ab + b = ab – b ………. (5)
4 = b ………. (6)
a = 1, b = 4

Question 7.
If A = \(\left[ \begin{matrix} 1 & 2 & 2 \\ 2 & 1 & -2 \\ a & 2 & b \end{matrix} \right] \)
the equation AA^T = 9I, where I is 3 × 3 identity matrix, then the ordered pair (a, b)
is equal to
(1) (2, -1)
(2) (- 2, 1)
(3) (2, 1)
(4) (- 2, – 1)
Answer:
(4) (- 2, – 1)

Explaination:


Equating the like entries
a + 2b + 4 = 0 …………. (1)
2a – 2b + 2 = 0
a – b + 1 = 0 …………. (2)
a² + b² + 4 = 9 …………. (3)

3b = – 3 ⇒ b = -1
Substituting in equation (1) we get
a + 2 × – 1 + 4 = 0
a – 2 + 4 = 0
a = – 2
Substituting the values a = – 2 , b = – 1 in equation (3)
we have
(- 2)² + (-1)² + 4 = 9
4 + 1 + 4 = 9
9 = 9
∴ The required value of the ordered pair (a, b) is
(a, b) = (- 2, – 1)

Question 8.
If A is a square matrix, then which of the following is not symmetric?
(1) A + A^T
(2) AA^T
(3) A^TA
(4) AA^T
Answer:
(4) AA^T

Explaination:
Given A is a square matrix.
A square matrix A is symmetric if A^T = A

(1) A + A^T
(A + A^T)^T = A^T + (A^T)^T
= A^T + A = A + A^T
∴ A + A^T is symmetric.

(2) AA^T
(AA^T)^T = (A^T)^TA^T
= AA^T
∴ AA^T is symmetric.

(3) A^TA
(A^TA)^T = A^T(A^T)^T
= A^TA
∴ A^TA is symmetric.

(4) A – A^T
(A – A^T)^T = A^T – (A^T)^T
= A^TA
∴ A – A^T is not symmetric.

Question 9.
If A and B are symmetric matrices of order n , where (A ≠ B) , then
(1) A + B is skew – symmetric
(2) A + B is symmetric
(3) A + B is a diagonal matrix
(4) A + B is a zero matrix
Answer:
(2) A + B is symmetric

Explaination:
Given A and B are symmetric matrices of order n.
∴ A^T = A and B^T = B
A matrix A is skew symmetric if A^T = – A
(1)(A + B)^T = A^T + B^T = A + B
A + B is not skew symmetric.
(2)(A + B)^T = A^T+B^T = A + B
∴ A + B is symmetric.
(3) A + B is a diagonal matrix is incorrect.
(4) A + B is a zero matrix is incorrect.

Question 10.
If A = \(\left[ \begin{matrix} a & x \\ y & a \end{matrix} \right] \) and if xy = 1, then det (AA^T) is equal to
(1) (a – 1)²
(2) (a² + 1)²
(3) a² – 1
(4) (a² – 1)²
Answer:
(4) (a² – 1)²

Explaination:

= (a² + x²) (y² + a²) – (ax + ay) (ax + ay)
= a² y² + a⁴ + x² y² + a² x² – ((ax)² + (ay)² + 2 (ax)(ay))
= a² x² + a² y² + a⁴ + (xy)² – a² x² – a² y² – 2a² xy
= a⁴ + (1)² – 2a²(1)
= a⁴ – 2a² + 1
|AA^T| = (a² – 1)²

Question 11.
The value of x, for which the matrix A = \(\left[ \begin{matrix} { e }^{ x-2 } & { e }^{ 7+x } \\ { e }^{ 2+x } & { e }^{ 2x+3 } \end{matrix} \right] \) is singular
(1) 9
(2) 8
(3) 7
(4) 6
Answer:
(2) 8

Explaination:

Question 12.
If the points (x, – 2), (5, 2), (8, 8) are collinear , then x is equal to
(1) – 3
(2) \(\frac{1}{3}\)
(3) 1
(4) 3
Answer:
(4) 3

Explaination:
Let the given points be (x₁, y₁) = (x, – 2) ,
(x₂, y₂) = (5, 2) and (x₃, y₃) = (8, 8)
The condition for the three points (x₁, y₁), (x₂, y₂) and (x₃, y₃) to be collinear is

\(\frac{1}{2}\) [x(2 – 8) + 2(5 – 8) + 1(40 – 16)] = 0
x × – 6 + 2 × – 3 + 1 × 24 = 0
– 6x – 6 + 24 = 0
– 6x + 18 = 0
6x = 18 ⇒ x = \(\frac{18}{6}\) = 3
x = 3

Question 13.
If \(\left| \begin{matrix} 2a & { x }_{ 1 } & { y }_{ 1 } \\ 2b & { x }_{ 2 } & { y }_{ 2 } \\ 2c & { x }_{ 3 } & { y }_{ 3 } \end{matrix} \right| \) = \(\frac{\text { abc }}{2}\) ≠ 0, then the area of the triangle whose vertices are

(1) \(\frac{1}{4}\)
(2) \(\frac{1}{4}\)abc
(3) \(\frac{1}{8}\)
(4) \(\frac{1}{8}\)abc
Answer:
(3) \(\frac{1}{8}\)

Explaination:

Question 14.
If the square of the matrix \(\left[ \begin{matrix} α & β \\ γ & -α \end{matrix} \right] \) is the unit matrix of order 2, then α, β, and γ should
(1) 1 + α² + βγ = 0
(2) 1 – α² – βγ = 0
(3) 1 – α² + βγ = 0
(4) 1 + α² – βγ = 0
Answer:
(1) 1 + α² + βγ = 0

Explaination:

– α² – βγ = 1
α² + βγ + 1 = 0

Question 15.

(1) Δ
(2) kΔ
(3) 3 kΔ
(4) k³ Δ
Answer:
(4) k³ Δ

Explaination:

Question 16.
A root of the equation \(\left| \begin{matrix} 3-x & -6 & 3 \\ -6 & 3-x & 3 \\ 3 & 3 & -6-x \end{matrix} \right| \) = 0 is
(1) 6
(2) 3
(3) 0
(4) -6
Answer:
(3) 0

Explaination:


0 = 0
x = 0 satisfies the given equation.
Hence the root of the given equation is x = 0.

Question 17.
The value of the determinant of A = \(\left[ \begin{matrix} 0 & a & -b \\ -a & 0 & c \\ b & -c & 0 \end{matrix} \right] \) is
(1) -2 abc
(2) abc
(3) 0
(4) a² + b² + c²
Answer:
(3) 0

Explaination:

= 0 – a(0 – bc) – b (ac – 0)
= abc – abc = 0

Question 18.
If x₁, x₂, x₃ as well as y₁, y₂, y₃ are in geometric progression with the same common ratio, then the points (x₁, y₁), (x₂, y₂), (x₃, y₃) are
(1) vertices of an equilateral triangle
(2) vertices of a right angled triangle
(3) vertices of a right angled isosceles triangle
(4) collinear
Answer:
(4) collinear

Explaination:
Given x₁, x₂ , x₃, as well as y₁, y₂, y₃, are in geometric progression with the same common ratio.
∴ x₁ = a, x₂ = ar, x₃ = ar² ,
y₁ = b, y₂ = br, y₃ = br²
(x₁, y₁) = (a, b),
(x₂, y₂) = (ar ,br)
and (x₃, y₃) = (ar², br²)
Area of the triangle whose vertices are
(x₁, y₁),(x₂, y₂) and (x₃ y₃) is

= \(\frac{1}{2}\)ab[1(r – r²) – 1 (r – r²) + 1 (r³ – r³)]
= \(\frac{1}{2}\)ab[r – r² – r + r² + 0]
= \(\frac{1}{2}\)ab × 0 = 0
∴ The points (x₁, y₁),(x₂, y₂) and (x₃ y₃) are collinear.

Question 19.
If denotes the greatest integer less than or equal to the real number under consideration and – 1 ≤ x< 0, 0 ≤ y < 1, 1 ≤ z < 2 , then the value of the determinant

(1)
(2)
(3)
(4)
Answer:
(1)

Explaination:

Question 20.
If a ≠ b, b, c satisfy \(\left| \begin{matrix} a & 2b & 2c \\ 3 & b & c \\ 4 & a & b \end{matrix} \right| \) = 0 then abc =
(1) a + b + c
(2) 0
(3) b³
(4) ab + bc
Answer:
(3) b³

Explaination:

(a – 6) (b² – ac) = 0
Since a ≠ 6 , we have a – 6 ≠ 0
∴ b² – ac = 0
b² = ac
b³ = abc

Question 21.
If A = \(\left| \begin{matrix} -1 & 2 & 4 \\ 3 & 1 & 0 \\ -2 & 4 & 2 \end{matrix} \right| \) and B = \(\left| \begin{matrix} -2 & 4 & 2 \\ 6 & 2 & 0 \\ -2 & 4 & 8 \end{matrix} \right| \), then B is given by
(1) B = 4A
(2) B = – 4A
(3) B = – A
(4) B = 6A
Answer:
(2) B = – 4A

Explaination:

Question 22.
IfA skew-symmetric of order n and C is a column matrix of order n × 1, then C_T AC is
(1) an identity matrix of order n
(2) an identity matrix of order I
(3) a zero matrix of order 1
(4) an identity matrix of order 2
Answer:
(3) a zero matrix of order 1

Explaination:
Given A is a skew symmetric matrix of order n.
∴ A^T = – A
C is a column matrix of order n × 1
C^Tis of order 1 × n
∴ C^T A is of order (1 × n) × (n × n) = (1 × n)
C^TAC is of order (1 × n) × (n × 1) = (1 × 1)
Since A is a skew – symmetric matrix, we have
A^T = -A
(C^T AC)^T= C^T A^T (C^T)^T = C^T (-A) C
= -C^T AC
∴ C^TAC is a skew – symmetric matrix.
A matrix of order 1 is skew – symmetric if A is zero matrix.
Since C^TAC is a skew – symmetric and its order is 1.
∴ C^TAC is a zero matrix.

Question 23.
The matrix A satisfying the equation

(1)
(2)
(3)
(4)
Answer:
(3)

Explaination:

x + 3z = 1 ——– (1)
y + 3t = 1 ——- (2)
z = 0
t = – 1
(1) ⇒ x + 3 × 0 = 1 ⇒ x = 1
(2) ⇒ y + 3 × – 1 = 1 ⇒ y = 4
∴ A = \(\left[ \begin{matrix} 1 & 4 \\ 0 & -1 \end{matrix} \right] \)

Question 24.
If A + 1 = \(\left[ \begin{matrix} 3 & -2 \\ 4 & 1 \end{matrix} \right]\), then (A + I) (A – I) is equal to
(1)
(2)
(3)
(4)
Answer:
(1)

Explaination:

Question 25.
Let A and B be two symmetrh matrices of same order. ^Then which one of the following statement is not true?
(1) A + B is a symmetric matrix
(2) AB is a symmetric matrix
(3) AB = (BA)^T
(4) A^TB = MI^T
Answer:
(2) AB is a symmetric matrix

Explaination:
Given A and B are two symmetric matrices of the same order.
A = A^T , B = B^T
(1)(A+B)^T = A^T + B^T = A + B
A + B is symmetric.

(2) (AB)^T = B^T A^T BA
Thus (AB)^T ≠ AB
Hence , AB is not symmetric.

(3) AB = (BA)^T
= A^T B^T = AB
Statement is true.

(4) A^T B = AB^T Since A^T = A
B = B^T
Statement is true.

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th English Guide Pdf Prose Chapter 4 Tight Corners Text Book Back Questions and Answers, Summary, Notes.

Tamilnadu Samacheer Kalvi 11th English Solutions Prose Chapter 4 Tight Corners

11th English Guide Tight Corners Text Book Back Questions and Answers

I. Choose the most appropriate answer for the following questions:

Question a.
‘Tight Corner’ means a _______.
i. difficult situation
ii. crowded corner
iii. tragic incident
iv. fierce fight
Answer:
i. difficult situation

Question b.
Barbizon refers to a _______.
i. kind of paint
ii. type of architecture
iii. region in Britain
iv. French school of painters
Answer:
i. kind of paint

Question c.
The narrator visited the sale-room as he _______.
i. wished to see an auction
ii. had a painting to sell
iii. was persuaded by his friend
iv. wanted to buy a painting
Answer:
iii. was persuaded by his friend

Question d.
The narrator had been a safe contributor at the auction, as _______.
i. there were bidders quoting higher prices
ii. he had a sound financial background
iii. his friend had lent him money
iv. he did not make any bidding
Answer:
i. there were bidders quoting higher prices

Question e.
“And I got it.” Here ‘it’ refers to the _______.
i. picture he wanted to buy
ii. money he asked for
iii. card to participate in the auction
iv. amount he had to pay
Answer:
ii. money he asked for

2. Answer the following questions:

Question a.
What is a tight corner? What happens when one finds oneself in a tight corner?
Answer:
Tight corner refers to the difficult or critical situation that one faces in his life. The person who finds himself in a tight corner becomes stressful both physically and mentally.

Question b.
What is the difference between a physical and mental tight comer?
Answer:
A physical tight corner is something which is visualized in person on spot. One can overcome this if he has extreme courageousness. Mental tight corner affects the whole system of a man as his mind is filled with stress till he comes out of it. In fact, it is more dangerous than physically tight corner.

Question c.
Why did the narrator visit Christie’s?
Answer:
The narrator visited Christie’s as his friend persuaded him to see the auction inside.

Question d.
The narrator heard his own voice saying,” and fifty”.What does this suggest?
Answer:
The narrator without his knowledge and any understanding of the situation said, ‘and forty’.

Question e.
What was the narrator’s financial condition?
Answer:
The narrator had exactly sixty-three pounds in the bank and he did not have securities even for five hundred pounds.

Question f.
The narrator could not pretend to have made a mistake in bidding. Why?
Answer:
The narrator could not pretend to have made a mistake in bidding because already he made many biddings earlier which made others think of him as a bloatocrat. Moreover, a genuine mistake of such a kind would have been rectified at once.

Question g.
What could have been the best way for the narrator, to get himself out of the tight comer?
Answer:
The best way for the narrator to get himself out of the tight corner was to confess his poverty to one of Christie’s staff and having the picture put up again.

Question h.
Why did the narrator feel he could have welcomed a firing party?
Answer:
It was his thought of bidding for fun which made him get caught in a tight corner. If he welcomed a firing party that would bring his death and he need not be humiliated in front of others.

Question i.
What was the bidder’s offer to the narrator?
Answer:
The bidder’s offer was to give fifty guineas to the narrator.

Question j.
How did the narrator take advantage of the situation?
Answer:
The narrator took advantage of the situation by asking a hundred guineas from the bidder who offered four thousand guineas for big Daubigny.

Text Inside Questions:

Question a.
Describe the activity that was going on in the saleroom at king street.
Answer:
The place was full. They were selling Barbizon pictures and getting tremendous sums even for little bits of things.

Question b.
What can you say about the author’s attitude when he high – handedly participated in the auction?
Answer:
An author is a nonchalant person who tries to have some fun in his life. At the same time, he knows his limitations.

Question c.
Why was the author sure he would not be caught?
Answer:
The author decided to bid safely by just raising the stake a little bit and leave it for real millionaires to go ahead. Thus he was sure that he would not be caught.

Question d.
What made the author ignore his friend’s warning?
Answer:
The author ignored his friend’s warning just because he liked to have some fun and was sure that he was not going to run any risks.

Question e.
How had the author managed the auction without getting involved in the deal?
Answer:
Although many bids ended up in four figures, they were started with a modest price of fifty to a hundred guineas only. He ventured till the figures reached only upto three digits. Thus he managed the auction without getting involved in the deal.

Question f.
What came as a shock to the author?
Answer:
There was bidding for four thousand guineas and as usual, he added fifty guineas to it. But to his surprise, none of them bid more than that.

Question g.
What did the falling of the hammer indicate?
Answer:
The falling of the hammer indicated “closure of the bid” and it mandated the highest bidder to pay and collect his purchase.

Question h.
What made the friend laugh heartily?
Answer:
The narrator had to pay four thousand and fifty guineas for his bidding. In reality, he had only sixty-three pounds. This made his friend laugh heartily.

Question i.
What kind of excuses did the narrator think he could make?
Answer:
The author speculated on the possibility of confessing his poverty to one of Christie’s staff and request to put up the picture for sale once again.

Question j.
Why did the friend desert the narrator, a second time?
Answer:
The narrator was standing on the outskirts of the little knot of buyers to pay the amount and get the picture. His friend who joined the narrator had a look at his face and could not control his laughter. Thus he deserted the narrator, a second time.

Question k.
How does the narrator describe the man who approached him?
Answer:
The man was a messenger of the high gods who wore a green baize apron and spoke in husky cockney tones.

Question l.
How does the Narrator show the presence of mind in the sudden turn of events?
Answer:
The man who bid for the picture first was ready to pay fifty guineas to the narrator. At that moment the narrator asked for a hundred guineas which shows his presence of mind.

Question m.
The narrator would not forget two things about his friend What are they?
Answer:
The author’s friend only persuaded him to go to Christie’s auction. Secondly, he was the only witness to the author ’s mental agony in trying to get out of the crisis.

3. Form a meaningful summary of the lesson by rewriting the numbers in the correct sequence:

1. The narrator had only 63 pounds with him and did not know how to manage the situation
2. The narrator thought of all his relations from whom he could borrow
3. Unfortunately, he had made the highest bid.
4. The narrator entered Christie’s as his friend persuade him to visit the sale-room.
5. Every time someone else made a higher bid and the narrator was not caught.
6. The narrator on a sudden impulse added 50 more guineas, to the amount offered.
7. His friend joined him then but left immediately unable to control his laughter.
8. He even thought of borrowing from moneylenders and confessing the truth to the staff at Christie’s.
9. The picture was declared sold to the narrator.
10. After some time a picture was put up and a bid for 4000 guineas was a raise
11. A sudden stroke of luck befell the narrator when he heard that the agent who had made the bid of 4000 guineas and buy the picture.
12. The narrator kept bidding just for fun.
13. The picture was given away to the other bidder and the narrator was saved from humiliation.
14. His friend had left the place roaring with laughter at the narrator’s predicament.
15. The narrator was quite happy at the offer but demanded 100 guineas instead of the 50. Now there was no need for him to make any payment.

Answers:

1. 8
2. 10
3. 6
4. 1
5. 5
6. 4
7. 12
8. 11
9. 7
10. 3
11. 13
12. 2
13. 15
14. 9
15. 14

4. Answer the following questions in a paragraph of about 100-150 words:

Question a.
Narrate the circumstances that led to the narrator getting into a tight corner, by his own folly.
Answer:
Lucas learned that an auction was in progress. His friend suggested that they peeped in, to watch the fun. Despite the caution from his friend, he started bidding at moderate rates. He had only 63 pounds in his account. A bidder was supposed to have a minimum of 500 pounds to take part in the bid. As bidding for most of the paintings were started with two or three digits in guineas, the author sailed through raising the stakes of many paintings and staying behind watching millionaires bid with higher prices. But one painting viz big Daubigny was launched at an offer price of 4000 Guineas.

Only one bidder showed interest. The rest were in silence. The author heard himself say “and fifty”. After seconds of uncomfortable silence, the dealer banged the hammer indicating the acceptance of the narrator’s offer of 4050 guineas for the painting. It was only then the narrator realized that he was in a tight comer. He wished a firing squad would be welcomed to eliminate him and put an end to his mental agony. He had no friend or relative or even money lenders who could extend him a loan to raise the money. He had got into a mess of his own choice.

“Auction houses run a rigged game. They know exactly how many people will be bidding on work and exactly who they are. In a gallery, works of art just need to pay. ”

Question b.
Trace the thoughts that went on in the mind of the narrator, when picture after picture was put up and sold at the auction.
Answer:
The narrator started bidding for fun and got into a difficult position of paying four thousand and fifty guineas for a picture which was useless for him. He had only sixty-three pounds with him and didn’t know how to pay for it.

He handed over his card to the clerk and without seeing the picture put for sale he, was thinking about the names of uncles and other persons from whom he might borrow money. He wondered of the money lenders who would as promissory notes.

He also thought of confessing his poverty to one of Christie’s staff and make them put up the picture again. All his thoughts ended in vain as the staff of Christie’s seemed unsympathetic and he was sure that they wouldn’t believe it to be a mistake.

Question c.
Explain how the narrator got out of the tight corner that he was in.
Answer:
When the author was perplexed beyond measure and was even ready to welcome a firing squad to bail him out of the current crisis, a divine chance presented itself to the narrator. The narrator had stupidly given an open bid to buy “big Daubigny” for 4050 guineas when he had only 63 pounds in his bank account.

However hard he tried, he could not recall the name of an “uncle” or a friend who could extend him a loan to cover the price of the painting. To delay disgrace, he was standing at the end of the queue of the successful bidders. Like a providential intervention, a mediator from the starting bidder who was ready to take the same painting for 4000 guineas enquired the narrator in a husky cockney tone if he was the gentleman who had bought, “big Daubigny”.

The narrator admitted it. To the narrator’s great relief, the mediator said the first bidder wanted to know if he would take 50 guineas for his interest. The author should have embraced him and wept for joy for bailing him out of a potential disgrace. But he made the best use of the opportunity exhibiting his guile, by asking him if that was the most he could offer. The mediator said that there was no harm in asking for some more. The narrator said he would take a hundred guineas. When the man left to find out the possibility both the author and his friend laughed.

But when the author saw the cheque for a hundred guineas, he became serious. He said with joy and shock, “of all the luck! well, I’m hanged”. Thus the narrator had a narrow escape from a tight comer. One could even say that the narrator escaped by the skin of his teeth.

“Call it a narrow escape, maybe it’s your lucky day. ”

Vocabulary:

Auction House Puzzler: (Text Book Page No. 111)

You have come across many terms associated with an auction, in the lesson. Now solve the crossword puzzle with words from the lesson. Make use of the clues given:

Across:

1. conducts auction
2. a protective garment
3. strip with numbers
4. offer

Down

1. painter
2. school of painting
3. auction house
4. painting

Answer:

Reading:

Read the following passage and answer the questions that follow:

The Stationmaster’s Supreme Sacrifice by Sanchari Pal (Adapted)

1. Thirty-three years ago, on the night of December 2, 1984, Bhopal was hit by a catastrophe that had no parallel in the world’s industrial history. An accident at the Union Carbide pesticide plant in Bhopal had released almost 30 tons of a highly toxic gas called methyl isocyanate, turning the city into a vast gas chamber.

The result was a nightmare; more than 600,000 people were exposed to the deadly gas cloud that left thousands dead and much more breathless, blind, and in agonizing pain. Few people know that during the Bhopal gas tragedy a heroic stationmaster risked his own life to save others.

2. On the evening of December 3, 1984, Ghulam Dastagir was settling down in his office to complete some pending paperwork. This work kept him in his office till lam in the night, when he emerged to check the arrival of the Gorakhpur Mumbai Express.

As he stepped on to the platform, the deputy stationmaster felt his eyes burn and a queer itching sensation in his throat. He did not know that poisonous fumes leaking from Union Carbide’s pesticide factory were stealthily enveloping the railway station.

3. Beginning to choke, Dastagir did not know then that twenty-three of his railway colleagues, including his boss, station superintendent Harish Dhurve, had already died. It was later reported that Dhurve had heard about the deadly gas and had immediately tried stopping the movement of trains passing through Bhopal before collapsing in his office chamber.

His suddenly worsening health and years of experience told Dastagirthat something was very wrong. Though he did not fully comprehend what was happening, he decided to act immediately when he did not get any response from the station master. He alerted the senior staff at nearby stations, like Vidisha and Itarsi, to suspend all train traffic to Bhopal.

4. However, the jam-packed Gorakhpur Kanpur Express was already standing at the platform and its departure time was 20 minutes away. Listening to his gut instinct, Dastagir summoned his staff and told them to immediately clear the train for departure. When they asked if they should wait until the order to do so came from the head office, Dastagir replied that he would take complete responsibility for the train’s early departure.

He wanted to ensure that the train left immediately, without any delay. His colleagues later recalled that Dastagir could barely stand and breathe as he spoke to them. Breaking all rules and without taking permission from anyone, he and his brave staff personally flagged off the train.

5. But Dastagir’s work was not done. The railway station was filling up with people, desperate to flee the fumes. Some were gasping, others were vomiting, and most were weeping. Dastagir chose to remain on duty, running from one platform to another, attending, helping, and consoling victims.

He also sent an SOS to all the nearby railway offices, asking for immediate medical help. As a result, four ambulances with paramedics and railway doctors arrived at the station. It was winter and the gas was staying low to the ground, a thick haze poisoning everything in its path.

Besieged by hordes of suffering people, the station soon resembled the emergency room of a large hospital. Dastagir stayed at the station, steadfastly doing his duty, knowing that his family was out there in the ill-fated city. That day all he had for his protection was a wet handkerchief on his mouth.

6. Ghulam Dastagir’s devotion to duty saved the lives of hundreds of people. However, the catastrophe didn’t leave him unscathed. One of his sons died on the night of the tragedy and another developed a lifelong skin infection.

Dastagir himself spent his last 19 years shuttling in and out of hospitals; he developed a painful growth in the throat due to prolonged exposure to toxic fumes. When he passed away in 2003, his death certificate mentioned that he was suffering from diseases caused as a direct result of exposure to MIC (Methyl Isocyanate) gas.

A memorial has been built at platform No.1 to pay tribute to those who sacrificed their lives in the line of duty on the fateful night of December 3, 1984. However, Ghulam Dastagir, who died later, is not one of them. A forgotten hero whose sense of duty and commitment saved countless lives, Dastagir’s story deserves to be recognized and remembered by our fellow countrymen.

Answer the following questions:

Question (i)
Why was the accident at union carbide unparalleled in the word’s industrial history?
Answer:
The accident was unparalleled in the world s Industrial history because it affected more than 600,000 people.

Question (ii)
How was Dastagir affected by the poisonous gas?
Answer:
He developed a painful growth in the throat due to prolonged exposure to toxic fumes.

Question (iii)
What was the action taken by the station superintendent?
Answer:
As soon as he heard about the deadly gas, he tried stopping the movement of trains through Bhopal.

ஆசிரியரைப் பற்றி:

எ.வே.லூக்காஸ் (1868-1938) ஒரு ஆங்கில நகைச்சுவை எழுத்தாளர், கட்டுரையாளர். நாடக ஆசிரியர், வாழ்க்கை வரலாற்று எழுத்தாளர், புத்தக வெளியீட்டாளர், கவிஞர், நாவலாசிரியர், சிறுகதை எழுத்தாளர், மற்றும் பத்திரிக்கை ஆசிரியர். லண்டன் புறநகர் பகுதியில் பிறந்தவர். தன் 16 வயதில் புத்தக விற்பனையாளரின் உதவியாளராக பணியாற்றியவர்.

பின்னர் பத்திரிக்கை துறையில் ஆர்வம் கொண்டு பிரிட்டனில் உள்ளூர் பத்திரிக்கையிலும், லண்டன் மாத இதழ் பத்திரிக்கையிலும் பணியாற்றினார். பெர்னார்ட் பார்ட்டன் என்ற குவாக்கர் கவிஞரின் வாழ்க்கை வரலாற்றை எழுத அவர் பணிக்கப்பட்டார்.

அதை சிறப்பாக எழுதியதால் சார்லஸ் லேம்பின் புத்தகங்களை மதிப்பிடும் வாய்ப்புக் கிடைத்தது. பின்பு இவர் 1904ல் பஞ்ச் என்ற இதழில் வாழ்நாள் முழுவதும் பணியாற்றினார். தன் சிறு கட்டுரைக்காக பிரபலமானார். பல பாடல்களையும், நாடகங்களையும் எழுதியுள்ளார்.

பாடச் சுருக்கம்:

இப்பாட பகுதியில் கதாசிரியர் தான் ஒரு இக்கட்டான சூழ்நிலையில் மாட்டிக் கொண்டு பின்னர் அதிலிருந்து எவ்வாறு தன் சாமர்த்தியத்தியத்தால் தப்பித்துக் கொள்கிறார் என்பதை தெளிவாக சொல்லியிருக்கிறார். தன் நண்பருடன் ஓவியங்களை ஏலம்விடும் இடத்திற்கு செல்கிறார்.

எல்லோரும் ஒவ்வொன்றாய் ஏலம்விட்டுக்கொண்டும், படங்களை வாங்கிக்கொண்டும் இருக்கையில் ஆசிரியர் விளையாட்டாக ஒரு ஓவியத்தை ஏலம் கேட்கிறார். ஆனால் இவரின் வங்கிக் கணக்கில் 63 பவுண்டுகள் மட்டுமே உள்ளது. ஆனால் விளையாட்டாக ஏலம் கேட்டிருக்கும் தொகையோ 4050 இனியாக்கள்.

விளையாட்டாக ஏலம் கேட்டு மாட்டிக் கொள்கிறார். இந்த சிக்கலாள தருனத்திலிருந்து தன் சமயோதித புத்திக்கூர்மையால் எப்படி இவர் இந்த இக்கெட்டான சூழ்நிலையில் இருந்து தன்னை காத்து கொள்கிறார் என்று இக்கட்டுரையில் விரிவாகக் காண்போம்.

Tight Corners Summary in Tamil

எங்கள் பேச்சி சிக்கலான நிலையில் மாட்டிக்கொள்ளும் நிகழ்வுகளைப்பற்றி ஓடிக்கொண்டிருந்தது, அதில் வாழத் தெரிந்தவர்கள் சாகசம் நிறைந்தவர்களாகவும் மற்றும் சமரசம் செய்ய தெரிந்தவர்களாகவும் இருப்பார்கள்.

ஒரு மனிதன் கடலோரப் பகுதியில் வடகிழக்கு France யில் பேரலையில் மாட்டிக்கொண்தாகவும், பின்பு சாமர்த்தியமாக தன் வலிமையினால் தப்பிவிட்டதாகவும் சொன்னார். மற்றொருவர் காயப்பட்ட புலியால் nதாக்கப்பட்டபோது யானையின் மீது இருந்தாக கூறினார்.

மூன்றாமவர் அவர் எரியும் வீட்டின் மூன்றாவது மாடியில் இருந்தார் எனவும் கூறினார். நான்காமவர் போரில் ஏவுகனையால் தாக்கப்பட்டார் எனவும் கூறினார்.

அவர்களில் ஒருவர் ஆனால் நீங்கள் எல்லோரும் உடல் ரீதியாக மாட்டிக்கொண்டவர்களை பற்றியே பேசுகிறீர்கள்”. கண்டிப்பாக அவர்கள் மனநிலையை விட உடல்நிலை இருக்கம் கொண்டவர்கள். நான் மிக மோசமான சிக்கலில் christies ல் இருந்தபோது சிக்கிக்கொண்டேன்”.

“Christie’s?” (க்ரைஸ்டீஸ்)

“ஆம். லண்டனில் பெரிதாக வணிகம் நடைபெறும் தெருவில் (St. Jame’s street) உள்ள எனது பழைய வெளிநாட்டு நண்பருடன் மதிய உணவு சாப்பிட்டேன், பின்னர் king streetயை கடந்தபோது, அவர் விற்பனை அறையை பார்வையிட என்னை வற்புறுத்தினார். அந்த இடம் மக்களால் நிறைந்து இருந்தது.

அவர்கள் Barbizon படங்களை விற்றனர், ஒவ்வொரு சிறு சிறு பொருட்களையும், படங்களையும் இரண்டாயிரம், மூவாயிரம் என நல்ல விலைக்கு விற்றனர். அவற்றில், காட்டுப்படங்கள், மாலை நேரத்து குளங்கள், மெய்ப்பர் ஆடுமேய்க்கும் சிறுவன் மற்றும் எப்போதும் போல உள்ள சாதாரன தலைப்பிலான படங்கள் இருந்தன.

எந்த ஏலமும் மூன்று இலக்க எண்களுக்கு மேல் ஏலத்திற்கு போகவில்லை. நான் வேடிக்கையாக ஏலத்தை கேட்டேன். என்னிடம் அறுபத்தி மூன்று பவுண்ட் மட்டுமே வங்கியில் இருந்தது. ஐந்நூறு பவுண்ட கடன் பெற நான் ஒரு பெரிய பணக்காரர் (bloatocrat) போல ஏல விற்பணையாளருடன் தலையை ஆட்டினேன்.

நீ கண்டிப்பாக மாட்டிக் கொள்வாய், என் நண்பன் என்னிடம் கூறினான் “இல்லை, நான் மாட்டிக்கொள்ள மாட்டேன்,” என்று கூறினேன். நான் எந்த விதமான இடர்களுக்கும் உள்ளாகமாட்டேன்” என்று நான் சொன்னேன்.

“நீண்ட நேரம் நான் சிக்கல் ஒன்றிலும் மாட்டிக்கொள்ளவில்லை ஒன்றும் செய்யவில்லை. பின்னர் ஒரு ஓவியத்தை ஏலத்திற்கு கொண்டுவந்தது வைத்தார்கள். சிவப்பு முகத்தை கொண்ட தொப்பியை அணிந்திருந்த ஒரு புதிய மனிதர் ஒரு படத்தை ஏலத்திற்காக முன்னே வைத்தார். யாரும் கேட்க இயலாத விலையை ஓவியத்திற்கு கேட்டு அனைவரையும் வியப்பில் ஆழ்த்தினர்.

முந்தைய ஏலம் (lots) நான்கு இலக்கங்களில் விற்கப்பட்டிருந்தாலம் ஐம்பது அல்லது நூறு Guineas என்று தொடங்கி, நான்கிலக்க எண்ணைத் தொட்டது. சிறப்பான முடிவை (crescendo) நோக்கி நான் அடிக்கடி பாதுகாப்பாக பங்களித்தேன். ஆனால் சிறிது நேரத்தில் புதியப்படம் வைக்கப்பட்டவுடன் வியாபாரி பரப்பரப்பாக ஆரம்பத் தொகையாக “நான்கு ஆயிரம் Guineas” என்று கூறினார்.

மிகுந்த சலசலப்பான உற்சாக ஒலி எழுந்தது. முடிவில் என் குரல் கூறியது, ”ஐம்பது!”. ஆழ்ந்த அமைதி நிலவியது. அப்போது ஏல அறிவிப்பாளர் ஏலத்தொகையை கேட்டவரையும் பின்பு எல்லோரையும் பார்த்தார்.

வியப்புடனும், அதிர்ச்சியுடனும் சிவப்பு முகம் வியாபாரி உயிரற்றவர் போல் தோன்றினார். அவர் தன்னுடைய பலத்தை பயன்படத்தியிருக்கிறார் என்று இப்போது நான் உணர்ந்தேன்.

“நான்கு ஆயிரத்து ஐம்பது Guineas வழங்கப்படும்”, திரும்பவும் அறையை நோட்டமிட்டுக்கொண்டு ஏலம் விடுபவர் கூறினார்.

எனது இதயதுடிப்பு நின்றது. இரத்தம் உறைந்தது (congealed). எந்த சத்தமும் இன்றி என் நண்பனின் கட்டுப்படுத்தப்பட்ட (smothered) சத்தம் மட்டுமே கேட்டது.

“நான்கு ஆயிரத்து ஐம்பது Guineas” நான்காயிரத்து ஐம்பதிற்கு ஏதாவது கேள்வி உண்டா ? பிறகு சுத்தியல் அடிக்கப்பட்டு ஏலம் முடிக்கப்பட்டது.

ஏல அறையின் உள்ளே இருக்க எனக்கு நெருக்கடியாக இருந்தது!, அறுபத்து மூன்று பவுன்டிற்கு நானூறு பவுன்ட் விலை மதிப்பு பெறாத எனக்கு பிடிக்காத அந்தப்படத்தை வேண்டாத, இந்நாளில் உயர்ந்த விலையான நான்காயிரத்து ஐம்பது guineas ற்கு வாங்கினேன்.

கனிவான ஆறுதல் பெற என் நண்பனை நோக்கி திரும்பினேன். நான் பார்த்தபோது என்னை தனியே விட்டு சென்றிருந்தான்; அந்த நிமிடம் பயந்தேன், ஆனால், என் நண்பன், தனிமையான இடத்தில் நின்று என் நிலையை பார்த்து சிரித்தான்.

நான் இதைக் கண்டு அதிர்ச்சியடைந்தேன். பணம் சேகரிப்பவரிடம் என் கார்டை ஒப்படைக்க நான் அங்கு இயல்பாக (nonchalantly) இருந்தேன். அடுத்து வரும் பிரச்சனையை சமாளிக்க நான் யோசித்தேன்- படங்கள் மேல் படங்கள் வந்து விற்பனை ஆகிறது .நான் எதையும் பார்க்கவில்லை.

நான் ஓடி சென்று கடன் வாங்க சாத்தியமாக இருக்குமென்று மாமாவின் (Uncles) பெயர் மனத்திரையுல் வருகிறதா எனப் பார்த்தேன். ஆனால் வரவில்லை. மறுபடியும் இப்படத்தை ஏலம் விட சாத்தியக்கூறு உள்ளதா? என வினவினேன். எனது ஏழ்மையை நான் Christies உள்ள ஒரு பணியாளரிடம் எடுத்துக்கூறினேன்.

அந்த படத்தை திரும்பவும் ஏலம் விட சொன்னேன். இதுதான் சிறந்த வழி – அனைத்து முயற்சியும் செய்தபிறகு நான் இந்த ஏலத்தை எவ்வாறு செய்ய போகிறேன், அந்த பணியாளர் வளமாக காட்சியளித்தாலும் இரக்கமற்றவர், இது ஒரு தவறு என்று யாரும் நம்பவில்லை. எத்தகைய தவறும் ஒரு நேரத்தில் சரி செய்யப்பட வேண்டும்.

சரியான நேரம் விற்பனை முடிவுக்கு வந்தது. நான் வியாபாரிகள் இருக்கும் வெளி இடத்திற்கு சென்றேன். அவர்கள் காசோலை எழுதிக்கொண்டும் வழிமுறைகள் சொன்னார்கள். எப்போதும் போல் நான்தான் கடைசி. அந்த நேரம் என் நண்பனுடன் சேர முயன்றேன், என்னை பார்த்தவுடன் அவன் கைக்குட்டையால் தன்முகத்தை மூடிக் கொண்டான்.

விதியின் படி நான் தனியாக விடப்பட்டேன் என் வாழ்நாளில் அதைபோல் முட்டாள்தனமாக நான் உணர்ந்ததில்லை. இரக்கமில்லாத மனிதரை பார்த்ததுமில்லை.

நேர்மையுள்ள வாழ்க்கையில் சில நேரங்களில் நல்லொழுக்கத்திற்கு அப்பால் வெகுமதிகள் பெற்றுள்ளது என்பதை உணர்ந்தேன். எனது காதில் ஒரு குரல் திடீரென சொன்னது, “மன்னித்துக் கொள்ளுங்கள், சார், நீங்கள் பெரிய மனிதர், பெரிய Daubigny படத்தை வாங்கிய சீமான் நீங்கள் தானே?”

“நான் தான் என்று ஒப்புக்கொண்டேன்”.

நன்று, நான்கு ஆயிரம் Guineas உங்களுக்கு அளித்தபெரிய மனிதர் உங்கள் ஏலத்தை ஐம்பது Guineasற்கு பெற்றுக் கொள்வீர்களா? என தெரிந்துகொள்ள நினைக்கிறார்.”

உயர்ந்த கடவுளின் தூதர் ஒரு கரடுமுரடான பச்சை கம்பளி மேலங்கி அணிந்து கொழகொழவென்ற Cockney குரலில் பேசினார். அவரை கட்டி தழுவி சந்தோசத்தில் நனைந்தேன். ஐம்பது Guineas எடுத்துகொண்டிருப்பேன். ஏன் நான் குறைந்த காசை (farthings எடுத்து) கொள்ள வேண்டும்.

”இது தான் கேட்கக் கூடிய அதிகபட்ச விலையா?” என்று கேட்டேன். “அவனிடம் சொல்லுங்கள் நான் நூறு எடுத்து கொள்கிறேன்”, நான் சொல்லி பிறகு பெற்றுக்கொண்டேன்.

என் நண்பனை நான் காணும் போது நானும் சிரித்து கொண்டிருந்தேன், ஆனால் அவன் அந்த காசோலை ‘ பார்த்தவுடன் மயங்கினான்”. “எல்லாம் அதிர்ஸ்டம். நல்லது நான் தொடங்குகிறேன்” என்றான்.

நான் அழைக்கவில்லையென்றால் நீ christies வந்திருக்க முடியாது என்பதை மறந்துவிடாதே” என்று நண்பன் சொன்னான், “நான் அதை மறக்க மாட்டேன்” என்று கூறினேன். “இது அழிக்கமுடியாத (indelibly) நெருப்பாக என் நெஞ்சில் இருக்கும். எனது முடி வெள்ளையாக மாறாது, பாருங்கள்?”

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 7 Matrices and Determinants Ex 7.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.4

Question 1.
Find the area of the triangle whose vertices are (0, 0), (1, 2) and (4, 3)
Answer:
The given points are (0, 0), (1, 2) and (4, 3)
Area of the triangle with vertices
(x₁, y₁), (x₂, y₂) and (x₃, y₃) is

∴ The area of the triangle with vertices
(0, 0), (1, 2) and (4, 3) is

Area cannot be negative. Taking positive value, we have
Required area Δ = \(\frac{5}{2}\) sq.units.

Question 2.
If (k, 2), (2, 4) and (3, 2) are vertices of the triangle of area 4 square units then determine the value of k.
Answer:
Given Area of the triangle with vertices (k, 2), (2, 4) and (3, 2) is 4 square units.
The area of the triangle with vertices
(x₁, y₁) , (x₂, y₂) and (x₃, y₃) is

Given Δ = 4, (x₁, y₁) = (k , 2), (x₂, y₂) = (2 , 4) and (x₃, y₃) = (3 , 2)

± 4 = k(4 – 2) – 2 (2 – 3) + 1(4 – 12)
± 4 = k × 2 – 2 × – 1 – 8
± 4 = 2k + 2 – 8
± 4 = 2k – 6
2k – 6 = 4 or 2k – 6 = -4
2k = 4 + 6 or 2k = – 4 + 6
2k = 10 or 2k = 2
k = 5 or k = 1
Required values of k are 1, 5.

Question 3.
Identify the singular and non – singular matrices.
(i) \(\left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \right] \)
(ii) \(\left[ \begin{matrix} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{matrix} \right] \)
(iii) \(\left[ \begin{matrix} 0 & a\quad -\quad b & k \\ b-\quad a & 0 & 5 \\ -k & -5 & 0 \end{matrix} \right] \)
Answer:
(i) \(\left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \right] \)

|A| = 1 (45 – 48) – 2(36 – 42) + 3(32 – 35)
|Al = – 3 – 2 × – 6 + 3 × – 3
|A| = – 3 + 12 – 9
|A| = – 12 + 12 = 0
∴ A is a singular matrix.

(ii) \(\left[ \begin{matrix} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{matrix} \right] \)
Answer:

|B| = 2(0 – 20) + 3 (- 42 – 4) + 5(30 – 0)
|B| = -40 + 3 × – 46 + 150
|B| = -40 – 138 + 150
|B| = -178 + 150 ≠ 0
∴ B is non singular.

(iii) \(\left[ \begin{matrix} 0 & a\quad -\quad b & k \\ b-\quad a & 0 & 5 \\ -k & -5 & 0 \end{matrix} \right] \)

|C| = 0 – (a – b) (0 + 5k) + k(-5 (b – a) – 0)
|C| = -5k (a – b) – 5k (b – a)
|C| = -5k (a – b) + 5k(a – b)
|C| = o
∴ C is a singular matrix.

Question 4.
Determine the values of a and b so that the following matrices are singular:
(i) A = \(\left[ \begin{matrix} 7 & 3 \\ -2 & a \end{matrix} \right] \)
(ii) B = \(\left[ \begin{matrix} b\quad -\quad 1 & 2 & 3 \\ 3 & 1 & 2 \\ 1 & -2 & 4 \end{matrix} \right] \)
Answer:
(i) A = \(\left[ \begin{matrix} 7 & 3 \\ -2 & a \end{matrix} \right] \)
|A| = \(\left[ \begin{matrix} 7 & 3 \\ -2 & a \end{matrix} \right] \)
|A| = 7a + 6
Given that A is singular
∴ |A| = 0
7a + 6 = 0 ⇒ a = \(\frac{-6}{7}\)

(ii) B = \(\left[ \begin{matrix} b\quad -\quad 1 & 2 & 3 \\ 3 & 1 & 2 \\ 1 & -2 & 4 \end{matrix} \right] \)
|B| = \(\left[ \begin{matrix} b\quad -\quad 1 & 2 & 3 \\ 3 & 1 & 2 \\ 1 & -2 & 4 \end{matrix} \right] \)
= (b – 1 )(4 + 4) – 2(12 – 2) + 3(- 6 – 1)
= 8 (b – 1) – 20 – 21
= 8b – 8 – 41
|B| = 8b -49
Given that B is singular
∴ |B| = 0
8b – 49 = 0 ⇒ b = \(\frac{49}{8}\)

Question 5.
If cos 2θ = 0, determine

Answer:
Given cos 2θ = 0

Question 6.
Find the value of the product

Answer:

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 7 Matrices and Determinants Ex 7.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.3

Solve the following problems by using Factor Theorem:

Question 1.
Show that \(\left| \begin{matrix} x & a & a \\ a & x & a \\ a & a & x \end{matrix} \right| \) = (x – a)² (x + 2a)
Answer:

By putting x = a , we have three rows of |A| are identical. Therefore (x – a)² is a factor of |A|
Put x = – 2a in |A|

∴ x + 2a is a factor of |A|. The degree of the product of the factors (x – a)² (x + 2a) is 3.
The degree of tfie product of the leading diagonal elements x . x . x is 3.
∴ The other factor is the contant factor k.

a³ [ – 1 (1 – 1) – 1 ( – 1 – 1) + 1 (1 + 1)] = k . 4a³
a³ [o + 2 + 2 ] = 4 ka³
4a³ = 4 ka³
k = 1

Question 2.
Show that \(\left| \begin{matrix} b\quad +\quad c & a\quad -\quad c & a\quad -\quad b \\ b\quad -\quad c & c\quad +\quad a & b\quad -\quad a \\ c\quad -\quad b & c\quad -\quad a & a\quad +\quad b \end{matrix} \right| \) = 8 abc
Answer:


since two columns identical
= bc × 0 = 0
∴ a – 0 is a factor. That is, a is a factor.
Put b = 0 in |A|

since two columns identical
= ca × 0 = 0
∴ b – 0 is a factor. That is, a is a factor.
Put c = 0 in |A|

since two columns identical
= ab × 0 = 0
∴ c – 0 is a factor. That is, c is a factor.
The degree of the product of the factors abc is 3.
The degree of the product of leading diagonal elements (b + c) (c + a) (a + b) is 3.
∴ The other factor is the constant factor k.

Question 3.
Solve that \(\left| \begin{matrix} x\quad +\quad a & b & c \\ a & x\quad +\quad b & c \\ a & b & x\quad +\quad c \end{matrix} \right| \) = 0
Answer:

Put x = 0

x = 0 satisfies the given equation. x = 0 is a root of the given equation, since three rows are identical. x = 0 is a root of multiplicity 2. Since the degree of the product of the leading diagonal elements (x + a) (x + b) (x + c) is 3. There is one more root for the given equation.
Put x = – (a + b + c)

∴ x = – (a + b + c) satisfies the given equation.
Hence, the required roots of the given equation are x = 0, 0 , – (a + b + c)

Question 4.
Show that \(\left| \begin{matrix} b\quad +\quad c & a & { a }^{ 2 } \\ c\quad +\quad a & b & { b }^{ 2 } \\ a\quad +\quad b & c & { c }^{ 2 } \end{matrix} \right| \) = (a + b + c) (a – b) (b – c) (c – a)
Answer:

Since two rows are idenctical
|A| = 0
since two rows are idenctical
|A| = 0
∴ a – b is a factor of | A |. The given determinant is in cyclic symmetric form in a , b and c. Therefore, b – c and c – a are also factors. The degree of the product of the factors (a – b) (b – c) (c – a) is 3 and the degree of the product of the leading diagonal elements (b + c) . b . c² is 4.
Therefore, the other factor is k (a + b + c).

5(18 – 12) – 1(36 – 12) + 1(12 – 6) = 12k
5 × 6 – 24 + 6 = 12k
30 – 24 + 6 = 12k
12 = 12 ⇒ k = 1

Question 5.
Solve \(\left| \begin{matrix} 4\quad -\quad x & 4\quad +\quad x & 4\quad +\quad x \\ 4\quad +\quad x & 4\quad -\quad x & 4\quad +\quad x \\ 4\quad +\quad x & 4\quad +\quad x & 4\quad -\quad x \end{matrix} \right| \) = 0
Answer:

Put x = 0

∴ x = 0 satisfies the given equation. Hence x = 0 is a root of the given equation. since three rows are identical, x = 0 is a root of multiplicity 2.

Since the degree of the product of the leading diagonal elements (4 – x) (4 – x) (4 – x) is 3. There is one more root for the given equation.


∴ x = – 12 is a root of the given equation.
Hence, the required roots are x = 0 , 0 , – 12

Question 6.
Show that \(\left| \begin{matrix} 1 & 1 & 1 \\ x & y & z \\ { x }^{ 2 } & { y }^{ 2 } & { z }^{ 2 } \end{matrix} \right| \) = (x – y) (y – z) (z – x)
Answer:

|A| = 0 since two columns identical
∴ x – y is a factor of A. The given determinant is in the cyclic symmetric form in x, y, and z. Therefore, y – z and z – x are also factors of |A|.

The degree of the product of the factors (x – y) (y – z) (z – x) is 3 and the degree of the product of the leading diagonal elements 1, y, z² is 3. Therefore, the other factor is the constant factor k.

Put x = 0, y = 1, z = -1 we get

Expanding along the first column
1 (1 + 1) = 2k
2 = 2k ⇒ k = 1

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 7 Matrices and Determinants Ex 7.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.2

Question 1.
without expanding the determinant,

Answer:

= s (a² + b² + c²) × 0
since two columns are equal.
= 0

Question 2.

Answer:

Question 3.
Prove that

Answer:



= 2abc [0 – b(0 – ac) + c(ab – 0)]
= 2 abc [ abc + abc ]
= 2 abc × 2abc
Δ = 4 a²b²c²

Question 4.
Prove that

Answer:

= a [b(1 + c) + c (1)] – 0 – c [0 – b]
= a[b + bc + c] + bc
= ab + abc + ac + bc
= abc + ab + bc + ac
= abc

Question 5.

Answer:

Question 6.
show that \(\left| \begin{matrix} x\quad +\quad 2a & y\quad +\quad 2b & z\quad +\quad 2c \\ x & y & z \\ a & b & c \end{matrix} \right| \) = 0
Answer:
Let Δ = \(\left| \begin{matrix} x\quad +\quad 2a & y\quad +\quad 2b & z\quad +\quad 2c \\ x & y & z \\ a & b & c \end{matrix} \right| \)

Question 7.
Write the general form of a 3 × 3 skew- symmetric matrix and prove that its determinant is 0.
Answer:
A square matrix A = [ a_ij ]3 × 3 is a skew – symmetric matrix if a_ij = – a_ij for all i,j and the elements on the main diagonal of a skew – symmetric matrix are zero.


= 0 – a₁₂ (0 + a₁₃ a₂₃) + a₁₃ (a₁₂ a₂₃ – 0)
= – a₁₂ a₁₃ a₂₃ + a₁₃ a₁₂ a₂₃
= 0
Hence the determinant of a skew – symmetric matrix is 0.

Question 8.

Prove that a, b, c are in G. P or α is a root of ax² + 2bx + c = 0.
Answer:

Question 9.

Answer:

Question 10.
If a, b, c are p^th, q^th and r^th terms of an A.P, find the value of \(\left| \begin{matrix} a & b & c \\ p & q & r \\ 1 & 1 & 1 \end{matrix} \right| \)
Answer:
Given a, b, c are p^th, q^th and r^th terms of an A.P.
t_p = a = A + (p – 1)D,
t_q = b = A + (q – 1)D,
t_r = c = A + (r – 1) D
where A – first term , D – Common difference of the AP.

Question 11.

Answer:

Question 12.
If a , b , c , are all positive, and are p^th, q^th and r^th terms of a G.P., show that \(\left| \begin{matrix} log\quad a & p & 1 \\ log\quad b & q & 1 \\ log\quad c & r & 1 \end{matrix} \right| \) – 0
Answer:
Given a, b, c are the p^th, q^th and r^th terms of a G.P.
∴ a = AR^p-1, b = AR^q-1, c = AR^r-1
where A is the first term , R – common ratio.

Question 13.
Find the value of

Answer:

Question 14.

Answer:

Question 15.
Without expanding, evaluate the following determinants:
(i) \(\left| \begin{matrix} 2 & 3 & 4 \\ 5 & 6 & 8 \\ 6x & 9x & 12x \end{matrix} \right| \)
(ii) \(\left| \begin{matrix} x\quad +\quad y & y\quad +\quad z & z\quad +\quad x \\ z & x & y \\ 1 & 1 & 1 \end{matrix} \right| \)
Answer:
(i) \(\left| \begin{matrix} 2 & 3 & 4 \\ 5 & 6 & 8 \\ 6x & 9x & 12x \end{matrix} \right| \)

(ii) \(\left| \begin{matrix} x\quad +\quad y & y\quad +\quad z & z\quad +\quad x \\ z & x & y \\ 1 & 1 & 1 \end{matrix} \right| [

Question 16.
If A is a Square, matrix, and |A| = 2, find the value of |A A^T|.
Answer:
|A| = 2 (Given) |A^T| = 2
Now |AA^T| = |A| |A^T| = 2 × 2 = 4.

Question 17.
If A and B are square matrices of order 3 such that |A| = -1 and |B| = 3, find the value of |3 AB|.
Answer:
Given |A| = -1 : |B| = 3
Given A and B are square matrices of order 3.
∴ |kAB| = k³ |AB|
Here k = 3 ∴ |3AB| = 3³ |AB|
= 27 |AB|
= 27 (-1) (3)
= -81

Question 18.
If λ = – 2, determine the value of

Answer:

Expanding along the first row
Δ = 0 + 4 [4 × 0 – (- 1 ) ( 13)] + [4 × -13 – 0 × – 1]
= 4 [0 + 13] + 1 [- 52 + 0]
= 52 – 52 = 0

Question 19.
Determine the roots of the equation
[latex]\left| \begin{matrix} 1 & 4 & 20 \\ 1 & -2 & 5 \\ 1 & 2x & { 5x }^{ 2 } \end{matrix} \right| \) = 0
Answer:
\(\left| \begin{matrix} 1 & 4 & 20 \\ 1 & -2 & 5 \\ 1 & 2x & { 5x }^{ 2 } \end{matrix} \right| \) = 0 ………… (1)
Put x = -1 then (1) ⇒

∴ x = – 1 satisfies equation (1)
Hence x = – 1 is a root of equation (1)
Put x = 2 then ……….. (1)

[Property 4: If two rows (columns) of a determinant are identical then its determinant value is zero.]

∴ x = 2 satisfies equation (1)
Hence x = 2 is a root of equation (1)
Hence the required roots are x = -1 , 2

Question 20.
Verify that det (AB) = (det A) (det B) for

Answer:

= 4 [-10 (0 – 9 × 19) – 5 (0 + 17 × 19) + 1 (32 × 9 + 17 × 26)]
= 4 [1710 – 5 × 323 + 288 + 442]
= 4 [1710 – 1615 + 730]
= 4 [2440 – 1615]
= 4 × 825
det (AB) = 3300 …….. (1)

= 4(0 – 21) – 3 (- 5 – 14) – 2 (3 – 0)
= -84 – 3 × – 19 – 6
= -84 + 57 – 6
= -90 + 57
det A = -33 ………… (2)

= 1 (20 – 0) – 3 (- 10 – 0) + 3 (-14 – 36)
= 20 + 30 + 3 × – 50
= 50 – 150
det A = – 100 ……….. (3)

From equations (2) and (3)
(det A) (det B) = – 33 × – 100
(detA) (det B) = 3300 ………… (4)
From equations (1) and (4), we have
det (AB) = (det A) (det B)

Question 21.
Using cofactors of elements of second row, evaluate |A|, where A = \(\left[ \begin{matrix} 5 & 3 & 8 \\ 2 & 0 & 1 \\ 1 & 2 & 3 \end{matrix} \right] \)
Answer:

|A| = a₂₁ A₂₁ + a₂₂ A₂₂ + a₂₃ A₂₃
= 2 × 7 + 0 × 7 + 1 × – 7
= 14 – 7
|A| = 7

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 7 Matrices and Determinants Ex 7.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.1

Question 1.
Construct an m × n matrix A = [a_ij], where a_ij is given by
(i) a_ij = \(\frac{(\mathbf{i}-2 \mathbf{j})^{2}}{2}\) with m = 2 , n = 3
(ii) a_ij = \(\frac{|3 \mathbf{i}-4 \mathbf{j}|}{4}\) with m = 3 , n = 4
Answer:
(i) a_ij = \(\frac{(\mathbf{i}-2 \mathbf{j})^{2}}{2}\) with m = 2 , n = 3
To construct 2 × 3 matrices.

(ii) a_ij = \(\frac{|3 \mathbf{i}-4 \mathbf{j}|}{4}\) with m = 3 , n = 4
To construct a 3 × 4 matrices.

Question 2.
Find the value of p, q, r and s if

Answer:

Equating the corresponding entries
⇒ p² – 1 = 1
⇒ p² = 1 + 1 = 2
p = ± \(\sqrt{2}\)
-31 – q³ = -4
-q³ = -4 + 31 = 27
q³ = -27 = (-3)³
⇒ q = -3
r + 1 = \(\frac{3}{2}\)
⇒ r = \(\frac{3}{2}\) – 1 = \(\frac{3-2}{2}\) = \(\frac{1}{2}\)
s – 1 = π
⇒ s = – π + 1 (i.e.,) s = 1 – π
So, p = ± \(\sqrt{2}\), q = -3, r = 1/2 and s = 1 – π

Question 3.
Determine the value of x + y if
\(\left[ \begin{matrix} 2x\quad +\quad y & 4x \\ 5x\quad -\quad 7 & 4x \end{matrix} \right] \) = \(\left[ \begin{matrix} 7 & 7y\quad -\quad 13 \\ y & x\quad +\quad 6 \end{matrix} \right]\)
Answer:
\(\left[\begin{array}{cc}{2 x+y} & {4 x} \\ {5 x-7} & {4 x}\end{array}\right]=\left[\begin{array}{cc}{7} & {7 y-13} \\ {y} & {x+6}\end{array}\right]\)
⇒ 2x + y = 7 ………….. (1)
4x = 7y – 13 ………….. (2)
5x – 7 = y …………… (3)
4x = x + 6 ……………. (4)
from (4) 4x – x = 6
3x = 6 ⇒ x = \(\frac{6}{3}\) = 2
Substituting x = 2 in (1), we get
2(2) + y = 7 ⇒ 4 + y = 7 ⇒ y = 7 – 4 = 3
So x = 2 and y = 3
∴ x + y = 2 + 3 = 5

Question 4.
Determine the matrices A and B if they satisfy 2A – B + \(\left[ \begin{matrix} 6 & -6 & 0 \\ -4 & 2 & 1 \end{matrix} \right] \) = 0 and A – 2B = \(\left[ \begin{matrix} 3 & 2 & 8 \\ -2 & 1 & -7 \end{matrix} \right] \)
Answer:

Question 5.
If A = \(\left[ \begin{matrix} 1 & a \\ 0 & 1 \end{matrix} \right] \), then compute A⁴
Answer:

Question 6.
Consider the matrix A_α = \(\left[ \begin{matrix} cos\quad α & -\quad sin\quad α \\ sin\quad α & cos\quad α \end{matrix} \right] \)
(i) Show that A_αA_β = A_(α+β)
Answer:

(ii) Find all possible real values α satisfying the condition A_α + A_α^T = I
Answer:

Question 7.
If A = \(\left[ \begin{matrix} 4 & 2 \\ -1 & x \end{matrix} \right] \) and such that (A – 2I) (A – 3I) = 0, find the value of x.
Answer:

Question 8.
If A = \(\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ a & b & -1 \end{matrix} \right] \), show that A² is a unit matrix.
Answer:

Question 9.
If A = \(\left[ \begin{matrix} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{matrix} \right]\) and A³ – 6A² + 7A + kI = 0, find the value of k.
Answer:

Equating the corresponding entries – 2 + k = 0 ⇒ k = 2
∴ The required value of k is k = 2

Question 10.
Give your own examples of matrices satisfying the following conditions in each case:
(i) A and B such that AB ≠ BA
(ii) A and B such that AB = 0 = BA, A ≠ 0 and B ≠ 0.
(iii) A and B such that AB = 0 and BA ≠ 0
Answer:
(i) A and B such that AB ≠ BA

(ii) A and B such that AB = 0 = BA, A ≠ 0 and B ≠ 0.

(iii) A and B such that AB = 0 and BA ≠ 0

Question 11.
Show that f(x) f(y) = f(x + y) , where f(x) = \(\left[ \begin{matrix} cos\quad x & -\quad sin\quad x & 0 \\ sin\quad x & cos\quad x & 0 \\ 0 & 0 & 1 \end{matrix} \right] \)
Answer:

Question 12.
If A is a square matrix such that A² = A, find the value of 7A – (I + A )³
Answer:
Given A² = A
So 7A – (I + A)³ = 7A – (I + 3A + 3A² + A³]
= 7A – I – 3A – 3 A² – A³
Given A² = A
7A – I – 3A – 3A – A³ = -I + A – A³
= -I + A – (A² × A)
= -I + A – (A × A) = -I + A – A²
= -I + A – A = -I
So the value of 7A – (I + A)³ = -I.

Question 13.
Verify the property A (B + C) = AB + AC, when the matrices A, B, and C are given by

Answer:

Question 14.
Find the matrix A which satisfies the matrix relation A\(\left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix} \right] \) = \(\left[ \begin{matrix} -7 & -8 & -9 \\ 2 & 4 & 6 \end{matrix} \right] \)
Answer:

Question 15.
If A^T = \(\left[ \begin{matrix} 4 & 5 \\ -1 & 0 \\ 2 & 3 \end{matrix} \right] \) and B = \(\left[ \begin{matrix} 2 & -1 & 1 \\ 7 & 5 & -2 \end{matrix} \right] \)
verify the following
(i) (A + B)^T = A^T + B^T = B^T + A^T
(ii) (A – B)^T = A^T – B^T
(iii) (B^T)^T = B
Answer:

(i) (A + B)^T = A^T + B^T = B^T + A^T

(ii) (A – B)^T = A^T – B^T

(iii) (B^T)^T = B

Question 16.
If A is a 3 × 4 matrix and B is a matrix such that both A^TB and BA^T are defined, what is the order of the matrix B?
Answer:
A is a matrix of order 3 × 4
So AT will be a matrix of order 4 × 3
AT B will be defined when B is a matrix of order 3 × n
BA^T will be defined when B is of order m × 4
from (1) and (2) we see that B should be a matrix of order 3 × 4

Question 17.
Express the following matrices as the sum of a symmetric matrix and a skew – symmetric matrix:
(i) \(\left[ \begin{matrix} 4 & -2 \\ 3 & -5 \end{matrix} \right] \)
Answer:



A = \(\frac{1}{2}\)(A + A^T) + \(\frac{1}{2}\)(A – A^T
Thus A is expressed as a sum of a symmetric and skew-symmetric matrix.

(ii) \(\left[ \begin{matrix} 3 & 3 & -1 \\ -2 & -2 & 1 \\ -4 & -5 & 2 \end{matrix} \right] \)
Answer:

Question 18.
Find the matrix A such that

Answer:

Equating like entries
2a – d = -1, 2b – e = – 8, 2c – f = -10
a = 1, b = 2, c = -5

2a – d = -1 ⇒ 2 × 1 – d = – 1
⇒ 2 + 1 = d ⇒ d = 3

2b – e = – 8 ⇒ 2 × 2 – e = – 8
⇒ 4 + 8 = e ⇒ e = 12

2c – f = -10 ⇒ 2 × – 5 – f = -10
⇒ – 10 – f = -10 ⇒ f = 0

Question 19.
If A = \(\left[ \begin{matrix} 1 & 2 & 2 \\ 2 & 1 & -\quad 2 \\ x & 2 & y \end{matrix} \right] \) is a matrix such that AA^T = 9I, find the values of x and y.
Answer:

Equating the corresponding entries
x + 4 + 2y = 0 ………… (1)
2x + 2 – 2y = o ………… (2)
x + 4 + 2y = 0 ………… (3)
2x + 2 – 2y = 0 ………… (4)
x² + 4 + y² = 9 ………… (5)

Substituting the value of y in equation (1) we have
x + 4 + 2x – 1 = 0
x + 4 – 2 = 0 ⇒ x = – 2
Substituting x = – 2 and y = – 1 in equation(5) we have
(5) ⇒ (-2)² + 4 + (- 1)² = 9
4 + 4 + 1 = 9
9 = 9
∴ The required values of x and y are
x = – 2 and y = – 1

Question 20.
(i) For what value of x, the matrix A = \(\left[ \begin{matrix} 0 & 1 & -\quad 2 \\ -\quad 1 & 0 & { x }^{ 3 } \\ 2 & -\quad 3 & 0 \end{matrix} \right] \) is skew – symmetric
Answer:

The matrix A is skew-symmetric if A = – A^T

Equating the corresponding entries
x³ – 3 = 0
x³ = 3 ⇒ x = 3^1/3

(ii) If \(\left[ \begin{matrix} 0 & p & 3 \\ 2 & { q }^{ 2 } & -\quad 1 \\ r & 1 & 0 \end{matrix} \right] \) is skew – symmetric find the values of p, q and r.
Answer:

A is skew-symmetric if A = – A^T

Equating the corresponding entries.
p = – 2 , r = – 3
q² = -q² ⇒ q² + q² = 0
⇒ 2q² = 0 ⇒ q = 0
∴ The required values are
p = – 2 , q = 0 , r = – 3

Question 21.
Construct the matrix A = [a_ij]_3×3 , where a_ij = 1 – j. State whether A is symmetric or skew – symmetric.
Answer:

a_ij = i – j
a₁₁ = 1 – 1 = 1
a₁₂ = 1 – 2 = – 1
a₁₃ = 1 – 3 = – 2
a₂₁ = 2 – 1= 1
a₂₂ = 2 – 2 = 1
a₂₃ = 2 – 3 = – 1
a₃₁ = 3 – 1= 2
a₃₂ = 3 – 2 = 1
a₃₃ = 3 – 3 = 0

Question 22.
Let A and B be two symmetric matrices. Prove that AB = BA if and only if AB is a symmetric matrix.
Answer:
Given A and B two symmetric matrices.
∴ A = A^T and B = B^T
First, let us assume AB = BA.
Let us prove AB is a symmetric matrix.

∴ AB is a symmetric matrix.
conversely let us assume that AB is a symmetric matrix.
we prove AB = BA
AB is symmetric then

Question 23.
If A and B are symmetric matrices of the same order, prove that
(i) AB + BA is a symmetric matrix
(ii) AB – BA is a skew-symmetric matrix.
Answer:
Given A and B are symmetric matrices
⇒ – A^T = A and B^T = B
(i) To prove AB + BA is a symmetric matrix.
Proof: Now (AB + BA)^T = (AB)^T + (BA)^T = B^TA^T + A^TB^T
= BA + AB = AB + BA
i.e. (AB + BA)^T = AB + BA
⇒ (AB + BA) is a symmetric matrix.

(ii) To prove AB – BA is a skew symmetric matrix.
Proof: (AB – BA)^T = (AB)^T – (BA)^T = B^TA^T – A^TB^T = BA – AB
i.e. (AB – BA)^T = – (AB – BA)
⇒ AB – BA is a skew symmetric matrix.

Question 24.
A shopkeeper in a Nuts and Spices shop makes gift packs of cashew nuts, raisins, and almonds. The pack contains 100 gm of cashew nuts, 100 gm of raisins, and 50 gm of almonds. Pack – II contains 200 gm of cashew nuts, 100 gm of raisins, and 100 gm of almonds. Pack -III contains 250 gm of cashew nuts, 250 gm of raisins, and 150 gm of almonds. The cost of 50 gm of cashew nuts is ₹ 50, 50 gm of raisins is ₹ 10, and 50 gm of almonds is ₹ 60. What is the cost of each gift pack?
Answer:

Let us consider 50 gm of cashew nuts as one unit, 50 gms of raisins as one unit 50 gm of almonds as one unit.
∴ The Gift pack matrix becomes

Also given 50 gms of Cashew nuts cost = Rs. 50
50 gms of Raisins cost = Rs. 10
50 gms of Almonds cost = Rs. 60
∴ Cost matrix is B = [50 10 60]
∴ Cost of cash gift pack = BA

∴ Cost of I gifts Pack = Rs. 180
Cost of II gift Pack = Rs.340
Cost of III gift Pack = Rs. 480

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th English Guide Pdf Prose Chapter 3 Forgetting Text Book Back Questions and Answers, Summary, Notes.

Tamilnadu Samacheer Kalvi 11th English Solutions Prose Chapter 3 Forgetting

11th English Guide Forgetting Text Book Back Questions and Answers

I. Based on your understanding of the essay, answer the following questions in one or two sentences each:

Question a.
What does Lynd actually wonder at?
Answer:
Robert Lynd wonders at the efficiency of human memory. He is amazed at the ordinary man’s capacity to remember phone numbers, addresses of friends, appointments for lunch and dinner and many names of actors, actresses and leading players in popular games.

Question b.
Name a few things that a person remembers easily.
Answer:
A person remembers telephone numbers, addresses of his friends, dates of good vintages, appointments for lunch and dinner, etc.

Question c.
How do psychologists interpret forgetfulness?
Answer:
Psychologists believe that humans forget what they don’t want to remember, like taking pills.

Question d.
What is the commonest type of forgetfulness, according to Lynd?
Answer:
According to Lynd the commonest type of forgetfulness occurs in the matter of posting letters.

Question e.
What does the author mean when he says the letter in his pocket leads an unadventurous life?
Answer:
The poet forgets the letters kept in his pocket. Whenever the friend enquires about the unposted letters, it embarrasses him. Then he is forced to produce the evidence of his guilt (i.e.,) the unposted letters. This awkward humiliation is said to be unadventurous.

Question f.
What are the articles the writer forgets most often?
Answer:
The writer forgets books, umbrellas, and walking sticks most often.

Question g.
Who are the citizens of dreamland? Why?
Answer:
Boys who return from cricket and football matches tend to forget bats and balls. Their minds are filled with a vision of the playing field. Their heads are among the stars. They are said to be the citizens of dreamland.

Question h.
What is common about the ‘angler’ and the ‘Poet’?
Answer:
The angler forgets his fishing rod and the poet forgets to post a letter just because their mind is filled with glorious matter.

2. Based on your reading, answer the following questions in two to four sentences each:

Question a.
What made people wonder about the absentmindedness of their fellow beings?
Answer:
The publication of articles lost by train travellers astonished many readers. Old people did not forget much. In fact, young men have forgotten bats and balls on their return from matches.

Question b.
What are our memories filled with?
Answer:
Our memories are filled with the names of actors and actresses, cricketers, footballers, and murderers.

Question c.
When does human memory work with less than its usual capacity?
Answer:
Human memory works with less than its usual capacity in matters like taking medicine. The author explains that human memory represents the willingness to remember certain things. It forgets what it does not wish to remember. Humans are blessed with “selective amnesia”

Question d.
Why according to Lynd should taking medicines be one of the easiest actions to remember?
Answer:
Taking medicines is one of the easiest actions to remember as it should be taken before, during or after meals. The meal itself is a reminder of it.

Question e.
How do the chemists make fortunes out of the medicines people forget to take?
Answer:
The forgotten medicines tend to aggravate the illness. Like a vicious cycle, again they are forced to buy costlier medicines. Thus people who forget to take medicines contribute to the fortunes of chemists.

Question f.
The list of articles lost in trains suggests that sportsmen have worse memories than their ordinary serious-minded fellows. Why does Lynd say this?
Answer:
Sportsmen have worse memories as when they return from the game they have their imagination still filled with a vision of the playing field. They are abstracted from the world outside them and their memories prevent them from remembering small prosaic things.

Question g.
What kind of absent-mindedness is regarded as a virtue by Lynd?
Answer:
Scientists, poets, anglers, and philosophers forget prosaic things. Their minds are absorbed in lofty thoughts and glorious imaginations that they forget ordinary things. Socrates, Tagore, and Einstein had the virtue of absent-mindedness. Einstein usually forgot to change his rocks. Once he even forgot his own house address. The absent-mindedness of such great personalities is a virtue. As they make the best of life, they have no time to remember the mediocre.

Question h.
Narrate the plight of the baby on its day out.
Answer:
The baby taken out by its father was left outside a public house just as the father slipped in for a glass of beer. His wife who came shopping saw the baby and took it home deciding to teach a lesson to her husband. To her surprise, the husband came forgetting all about the baby.

3. Answer the following in a paragraph of about 100-150 words each:

Question a.
You have borrowed a branded cricket bat from your reluctant friend for an outstation match. After returning home you realize you have absent-mindedly left it in the hotel room. Write a letter of apology and regret to your friend.
Answer:
822, Old Peter Road,
Trichy.

Dear Akshay,
Hope this letter of mine would find you in the best of health. First of all, I thank you very much for lending me your branded cricket bat for my match in Chennai. Though you were reluctant at first, you were kind enough to lend it to me later. I really played well with that bat and scored the highest run rate.

Truly it is the luckiest bat. After the match, I kept it safe in the hotel room where I stayed. Because of my weariness, I had a sound sleep that day and was in a hurry to catch my train for the return journey. In that hurry, I forgot to take your bat. Only after reaching Trichy, I realized that I absent-mindedly left your bat in the hotel room itself. I truly regret for the mistake committed by me and beg your pardon.

I know pretty well that it is your precious bat. I am also aware of the fact that you won’t forgive me easily for my action. I have made arrangements to bring back the bat here which may take some time. Kindly bear the inconvenience prevailed and try to forgive me.

With lots of regrets,

Yours affectionately,
Arun.

Question b.
Kahlil Gibran states ‘Forgetfulness is a form of freedom’ Write an article for your school magazine, linking your ideas logically and giving appropriate examples.
Answer:
Forgetting is deemed by many people leading prosaic lives as a mistake or an inefficiency of mind. But in reality, forgetfulness is freedom. Osho is right in his opinion of forgetfulness. In fact, it liberates painful memories and unpleasant things. We need to “let go” painful memories of the past and be free to aspire for better things in life. Robert Frost in his poem, “Let go” talks about a mediocre person’s inability to let go of things that hurt them. The capacity to forget hurtful memories is a real blessing.

If the human mind does not have the capacity to forget, life would be miserable for every one of us. The human mind is such a wonderful machine that it retains what is most important for personal or professional growth and allows the other things to slip away from the bank of memory. But young ones should remember to remember important assignments, deadlines for submission of homework, examination time-tables, and hall tickets before leaving for examination.

To assist memory we can have a checklist before leaving for school. It is often said, “If you fail to plan, you plan to fail.” So, my dear friends, I appeal to you to love whatever work you do. The brain retains in memory whatever you do with great passion, love, and involvement. For a successful life, a strong memory is indispensable. So, cultivate a strong memory. However, I appeal to you to forget failures, betrayals, and hurts to grow into a happy and healthy person.

“Sometimes we survive by forgetting.”

Question c.
Will you sympathize or ridicule someone who is intensely forgetful? Write an essay justifying your point of view.
Answer:
It is a general fact that all human beings are absent-minded at times. I really sympathize with the person who is intensely forgetful. His extreme level of forgetfulness reveals that he is a creative person and a genius. We have heard of great Scientists who are often forgetful. A person becomes absent-minded based on two facts.

One is when his mind is completely filled with stressful thoughts. Another reason is, he may be a creative person whose mind is always thinking of creating something new and forgets the present. Whatever be the reason there is no use ridiculing them.

On the other hand, we can help or guide them to note down important information in their diaries so that they can see to it when they forget something. In Kahlil Gibran’s point of view “Forgetfulness is a form of freedom”. So it can be rightly concluded that those who enjoy that freedom are really blessed.

d) Find the antonyms of the following words in the puzzle and shade them with a pencil. The first one has been done for you:

Answer:

1. Seldom x Often
2. admitted x denied
3. methodical x disorderly
4. reality x fantasy
5. fact x fiction.
6. virtue x vice
7. vile x good
8. indignant x delighted
9. relish x hate

Now, read the following biographical extract on Sujatha Rangarajan, a Science fiction writer, and answer the questions that follow:

1. Sujatha is the allonym of the Tamil author S. Rangarajan and it is this name that is recognized at once by the Tamil Sci-Fi reading community. You might have seen the Tamil movie ‘Endhiran’ where the robot Chitti exhibits extraordinary talents in an incredible manner. The robot could excel a human being in any act, beyond one’s imagination.

Jeeno, a robotic dog which appeared in Sujatha’s science fiction novel “En Iniya lyandhira” (My Dear Robot) formed the basis of Chitti’s character. Like Chitti, Jeeno was an all-rounder who could cook, clean, and fight. High-tech computer technology terms are used in the story. Jeeno, a pet robot, plays an important role throughout the story. As the story proceeds, it behaves and starts to think on its own like a human and instructs Nila, a human being, on how to proceed further in her crises.

2. In the preface of En lniya Iyandhira the writer states the reason for his attraction to the genre: Science gives us the wonderful freedom to analyse thousands and thousands of alternative possibilities. While using it, and while playing with its new games, a writer needs to be cautious only about one thing. The story should draw some parallels or association from the emotions and desires of the present humankind.

Only then it becomes interesting. Jeeno, the robot dog, was intelligent. But the character became popular only because of the robot’s frequently displayed human tendencies’ It is no wonder that all his works echo these words and will remain etched in the minds of the readers who enjoy reading his novels to have a wonderful lifetime experience.

3. It was Sujatha, who set the trend for sci-fi stories. He had tracked the origin from Mary Shelly’s Frankenstein to his short stories. He has written 50 sci-fi short stories and these were published in various Tamil magazines. His stories have inspired many readers to extend their reading to English sci-fi writers like Isaac Asimov.

The themes were bold, even if there was a dependence on very well – established characterization of English fiction. Sujatha opened up a new world to us with his writings on holograms, computers, and works like ‘En Iniya lyanthira’ inspire many to study computer science.

4. He has been one of the greatest writers for more than four decades. He combined reasoning and science in his writings. Being a multifaceted hi-fi and sci-fi humanistic author, he expressed his views distinctively. He was the one who took Tamil novels to the next level.

As an MIT alumnus and an engineer at BHEL, he was very good at technology. He could narrate sci-fi stories impressively. His readers always enjoyed reading all his detective and sci-fi novels which featured the most famous duo ‘Ganesh’ and ‘Vasanth’.

5. Sujatha has played a crucial role as a playwright for various Tamil movies which have fascinated movie lovers. Hence, it is fathomable that the writer’s perspective of future India enthuses every reader and paves a new way to reading sd-fl stories in English.

Find words from the passage which mean the same as the following:

Question 1.
difficult to believe (para 1)
Answer:
incredible

Question 2.
a style or category of art, music or literature (para2)
Answer:
genre

Question 3.
having many sides (para 4)
Answer:
multifaceted

Question 4.
capable of being understood (para 5)
Answer:
fathomable.

ஆசிரியரைப் பற்றி:

ராபர்ட் வில்சன் லிண்ட் (1879-1949) ஒரு ஐனஷ் எழுத்தாளர். 20ம் நூற்றாண்டில் வாழ்ந்த கட்டுரையாளர்களில் மிகச்சிறந்தவர். சிறந்த பத்திரிக்கையாளராக தன் பணியைத் தொடங்கினார். தினசரி செய்திதாள்’, ‘புதிய செய்தி, நாடு போன்ற பல பத்திரிக்கைகளில் அதிகமான கட்டுரைகளை எழுதியுள்ளரர்.

தன் படைப்புகள் அனைத்தும் வாசிப்பவரின் ஆர்வத்தை தூண்டக் கூடிய நகைச்சவை, மகிழ்ச்சி, வஞ்சப்புகழ்சி, விமர்சனம் அடிப்படையில் அமைந்திருக்கும்.

1947ல் இவருக்கு குயின்ஸ் பல்கலைக்கழகத்தால் இலக்கியத்திற்கான கௌரவ முனைவர் பட்டம் வழங்கப்பட்டது. இலக்கியத்திற்காக இவருக்கு ராயல் சொனசட்டியால் வெள்ளி பதக்கமும், டைம்ஸ் நிறுவனத்தால் தங்க பதக்கமும் வழங்கப்பட்டது. என்ற இந்த கட்டுரையில் மறதியை பற்றியும், அதன் இயல்பையும் நகைச்சுவையாக எழுதியுள்ளார்.

பாடத்தைப் பற்றி:

இந்த கட்டுரையில் ராபர்ட் லிண்ட் மனிதர்களில் உள்ள மறதிக்கான அடிப்படைக் காரணங்களைப் பற்றி தெளிவாக கூறுகிறார். நாம் எதை மறந்து போகிறோம், அப்படி மறந்து போவதால் ஏற்படும் விளைவுகள், ஏன் மறந்து போகிறோம் என்று பலவிதமான வினாக்களுக்க விடையையும் தருகிறார். மறத்தலைப் பற்றி தெளிவாக இக்கட்டுரையில் காண்போம்.

Forgetting Summary in Tamil

ரயிலில் செல்லும் பயணிகள் தவரவிட்ட பொருட்களை இப்போது லண்டன் நிலையத்தில் விற்பனைக்கு உள்ளதாக அறிவித்தனர். அதை வாசித்த மக்கள் அவர்கள் மறதி மனப்பாங்கை நினைத்து திகைத்தனர். புள்ளி விவரப்படி நான் சந்தேகப்பட்டது போல் இவ்வாறு மறந்து போகுதல் பொதுவான நிகழ்வுதான்.

இவை மனித நினைவின் திறன் மற்றும் திறன் இல்லாததை சொல்லி அதிசயப்பட வைக்கிறது. நவீன மனிதன் கைபேசி எண்களைக்கூட நினைவில் வைத்திருப்பான். அவன் நண்பரின் முகவரியையும் நினைவில் வைத்திருப்பான். பழங்காலத்தில் நடந்த நல்ல நிகழ்வுகளை கூட அவன் நினைத்துப்பார்க்கிறான்.

மதிய உணவு மற்றும் இரவு சாப்பாட்டிற்கான குறிப்பை அவன் ஞாபகம் வைத்திருப்பான். அவனது நினைவுகள் நடிகர், நடிகைகள், கிரிகிகெட் வீரர்கள் மற்றும் கால்பந்து வீரர்கள் மற்றும் கொள்ளையர்கள் என நெரிசலாக இருக்கும்.

கோடை காலத்தில் அவன் நன்றாக உணவு அருந்திய உயர்ரக ஹோட்டலையும், கடந்து சென்ற ஆகஸ்ட் பருவநிலையும் அவனால் சொல்ல முடியும். அவனது சாதாரண வாழ்விலும், அவன் எதையெல்லாம் நினைவு கூற நினைக்கிறானோ அதை அனைத்தையும் நினைவுப்படுத்துவான்.

லண்டனில் உள்ள ஆண்கள் எல்லோரும் காலையில் ஆடை அணியும் போது தங்களின் ஆடைகளின் சிறு துண்டினை மறப்பதுண்டா? நூற்றில் ஒருவர் கூட இல்லை. ஏன் ஆயிரத்தில் ஒருவர் கூட இல்லை. எத்தனை பேர் வீட்டை விட்டு வெளியில் செல்லும் போது வீட்டின் முன் கதவை அடைக்காமல் செல்வோம்.

ஒரு நாள் முழுதும் அவ்வாறு போகிறோம், நாம் படுக்கைக்கு செல்லும் வரை நமது செயலை தெளிவாக செய்கிறோம். ஆனால் ஒரு சாதாரண மனிதன் மேல் மாடிக்கு செல்வதற்கு முன் விளக்குகளை அணைக்க மறக்கிறான்.

சில நேரத்தில் நாம் நமது நினைவுகள் சாதாரணமாக செயல்படுவதை விட குறைந்து செயல்படும். ஒரு முதுநிலை மனிதர் மருத்துவர் அவருக்கு பரிந்துரை செய்ததை மறவாமல் எடுத்து செல்கிறார் என நினைக்கிறேன்.

இது ஆச்சரியம் தரக்கூடிய விஷயம் தான். மருந்துகள் என்பது இயல்பாக நம் நினைவில் இருக்கக்கூடியவை. விதியின் அடிப்படையில் அவை சாப்பாட்டிற்கு முன் அல்லது சாப்பாட்டிற்கு பின்பு மற்றும் உணவு என்ன என்பது கூட நினைவில் இருக்கும்.

உண்மை என்னவென்றால் சில ஒழுக்க அரக்கர்கள் அவர்களது மருந்துகளை ஞாபகம் வைத்திருப்பார்கள்.சில உளவியலாளர்கள் நம்மிடம் கூறுவது நாம் மறக்க நினைக்கும் விஷயத்தை மறக்கிறோம், ஏனெனில் அவை மிகுந்த வெறுப்பான மருந்தாக இருக்கும்; மனிதர்கள் குறிப்பிட்ட நேரத்தில் சாப்பிட மறக்கிறார்கள்.

என்னைப்போல் மருந்துக்கு நீண்ட பக்தனாக இருப்பவர்கள் வெறுப்பாக ஆர்வமில்லாமல் (unwillingly) மறந்து விடுகிறோம். புதிய, பரவலாக விளம்பரப்படுத்தப்படும் சிகிச்சை எனக்கு மிகவும் மகிழ்ச்சியளிக்கிறது.

நான் மருந்துகளை என் பையில் வைத்திருந்தாலும், அதை மறந்து, ஒரு மணி நேரம் கழித்து அதை எடுத்து சாப்பிடுவேன். மருத்துவரின் பொக்கிஷம் (fortunes)அவரின் மருந்தை மக்கள் மறந்து சாப்பிடாமல் இருப்பது.

பொதுவாக நான் மறந்துபோவதாக நினைப்பது கடிதம் அனுப்புவதிலே. பொதுவாக என்னை பார்க்க (சந்திக்க) வருபவரிடம் தயக்கத்துடன் எனது முக்கியமான கடிதத்தை அனுப்ப சொல்வேன். கடிதத்தை கொடுக்கும் முன் என் மீது நம்பிக்கை வர வைப்பேன். என்னிடம் கடிதத்தை அனுப்ப சொல்பவர்கள் என்னைப்பற்றி முழுதும் அறியாதவர்கள்.

நானே எடுத்து சென்றாலும் ஒரு பில்லர் பெட்டியை தாண்டிய பிறகு அடுத்த பெட்டியில் போட ஞாபகம் வரும். கையில் வைத்திருப்பது பதிலாக அதை என் சட்டை பையில் வைத்து அப்படியே மறந்துவிடுவேன்.

அதன் பிறகு, இது ஒரு மகிழ்ச்சியில்லா வாழ்க்கை. சங்கிலிப்போன்ற பிரச்சனைகள், எண்ணற்ற சொல்லமுடியா கேள்விகளை கேட்பது போன்று, என்னை வற்புறுத்தி என்னுடைய குற்ற உணர்வுகளை வெளிப்படுத்த வைக்கும்.

இவை அனைத்தும் மற்றவரின் கடிதம் என்பதால் ஈடுபாடு இல்லாமல் இருக்கலாம், சில கடிதங்கள் நான் எழுத நினைத்தது கூட நான் அனுப்ப மறந்துள்ளேன்.

நான் ரயிலில், Taxi யில் பொருட்களை தவறவிட்டவர்களைப் போல மிகச்சிறந்த மறதியாளன் அல்ல. என் புத்தகத்தையும், Walking stick யும் தவிர மற்ற எல்லாவற்றையும் நினைவுபடுத்திக் கொள்வேன். Walking stick வைத்திருப்பது நடக்க கூடிய காரியம் அல்ல. பழையகால ஆசை அதன் மேல் உண்டு, அடிக்கடி நான் அதை வாங்குவேன்.

எனது நண்பன் வீட்டுக்கு அல்லது ஒரு ரயில் பயணத்திற்கு பிறகு மற்றொன்றை தொலைத்துவிடுவேன். தொலைத்து விடுவேன் என்ற பயத்தில் குடை எடுத்து செல்வதில்லை. வாழ்வில் குடையை நான் தொலைத்தது இல்லை – குள்ளமான குடையை கூட தொலைத்தது உண்டா?

நம்மில் பலர், ஞாபகம் மறதியால் பல பொருட்களை பயணங்களில் இழந்திருக்கிறோம். சாதாரண மனிதன் சேரவேண்டிய இடத்தை அடையும் போது தன் பையையும் பொருளை பத்திரமாக கொண்டு செல்கிறான். அந்த ஆண்டில் ரயிலில் பொருட்களை தவறவிட்டவர்களின் பட்டியலில் பெரும்பாலானோர் இளைஞர்களே. சாதாரண மனிதனை விட விளையாட்டு வீரனுக்கு ஞாபகமின்மை அதிகமாக உள்ளது.

கிரிக்கெட் பேட், கால்பந்து போன்ற எண்ணிலடங்கா பொருட்களே மறக்கப்பட்டுள்ளன. தெளிவாக புரிந்துகொள்ள, ஆண்கள் விளையாடி விட்டு வீடு திரும்பும் போது விளையாட்டு திடலின் நினைவே இருக்கும் – அவர்கள் தலைவர்கள் நட்சத்திரங்கள் மத்தியிலும் – அவர்கள் சிறந்த செயல் (exploit) மற்றும் குறைகளை நினைத்து பார்ப்பார்கள்.

நினைக்க கூடிய (Abstracted) வகையில் உலகம் அவர்களுக்கு வெளியே இருக்கும். நினைவுகளில் சில மந்தமான (Prosaic) செயல்கள் அவர்களுடன் எடுத்து செல்ல நேரிடும்.

மீதி நாட்களில் அவர்கள் கனவு உலகத்தின் குடியுரிமை கொண்டவர்கள். இதேபோல், சந்தேகமின்றி, மீன்பிடிப்பவர்கள் தூண்டிலை மறப்பார்கள். பொதுவாக மீன் பிடிப்பவரை சொல்வது எதன் அடிப்படையில் நியாயப்படுத்த என தெரியவில்லை.

மனிதர்களிள் அவர்கள்தான் கற்பனையாளர்கள், அம்மனிதன் புதிதாக உருவாக்கும் கற்பனையோடு அவன் வீட்டுக்கு செல்லும் போது அது அவன் குணங்களின் சிறு மறதிமனப்பாங்கு தன்மையை காட்டுகிறது.

எதார்த்ததில் மீன் பிடிப்பதை அவர் மறந்துவிட்டு பிறகு Utopia மீன்பிடிப்பை, அச்சத்தை மீறி கற்பனை செய்கிறார். விளையாட்டின் நினைவுகளை மறப்பது நன்மைதான். அவன் மீன்பிடிப்பை மறக்கலாம். ஒருகவிஞன் தனது கடிதத்தை மறக்கலாம், ஏனெனில் அவர் சிந்தனை முற்றிலும் பெருமைக்குரிய விஷயங்கள் நிறைந்திருக்கும்.

மறதிமனப்பான்மை என்னை பொறுத்தவரை சிறந்த குணம்தான். மறதிமனப்பான்மை கொண்டவனது வாழ்க்கை சிறந்ததாக இருக்கும். சாதாரண (mediocre) விஷயங்கள் நினைவுப்படுத்த அவனுக்கு நேரம் இருக்காது. Socrates அல்லது Coleridge நம்பி கடிதத்தை அனுப்ப சொல்வதற்கு சமம்? அவர்களுக்கு செயலில் ஆர்வம் உள்ளது.

கேள்வி என்னவென்றால் நல்ல நினைவுகளை தக்கவைப்பது நல்லது என்று அடிக்கடி பேசப்பட்டு வருகிறது. மனிதனின் தவறான நினைவுகளில் தான் சிறந்தவன் என தோன்றும். அனைத்தும் நினைவில் வைத்திருக்கும் மனிதன் இயந்திரம். அவன் முதல் அறிவாளி என மதிக்கப்படுவான்.

சில இடங்களில் குழந்தைகள் மற்றும் மனிதரின் சிறந்த நினைவுகளை பேச சிறந்தவன் இல்லை. சிறந்த எழுத்தாளர்கள், இசை உருவாக்குபவர்கள் மொத்தத்தில் மிகுந்த ஆற்றல் கொண்ட நினைவுகள் கொண்டவர்கள் என நான் நினைக்கிறேன். நினைவுகள் தான் அவர்கள் கலையின் பாதி சகாப்தம்.

அடுத்ததாக அரசியல் மேதைகள் முற்றிலும் மோசமான நினைவாற்றால் கொண்டவர்கள். இரண்டு அரசியல் மேதைகளை ஒரே செயலைப்பற்றி பேச செய்தால் என்ன நடக்கும். எடுத்துக்காட்டாக அமைச்சரவைக் கூட்டத்தில் ஒவ்வொருவரும் மற்றொருவர் கதையை உண்மையாக வடித்து (seive) தைரியமாக (grid) உரைப்பார்கள்.

ஒவ்வொரு அரசியல் வாதியின் சுயகுறிப்பு மற்றும் பேச்சு மொழி சவால் நிறைந்ததாக இருக்கும் , இந்த உலகம் இன்னும் சிறந்த அரசியல் வாதியை கொண்டுவரவில்லை. ஒரு சிறந்த கவிஞன் மிகுந்த நினைவாற்றல் மற்றும் புத்திகூர்மை உள்ளவனாக இருக்க வேண்டும்.

அதே நேரத்தில், சிறந்த நினைவாற்றால் கொண்ட மனிதரை மதிக்க வேண்டும். நான் ஒரு அப்பாவை அறிந்தவரை அவர் குழந்தையை (Perambulator) குழந்தைகளுக்கான வண்டியில் வைத்து அதிகாலையில் பொது இடம் ஒன்றுக்கு பீர் அருந்த சென்றார்.

சிறிது நேரம் கழித்து அவரது மனைவி அதே இடத்திற்கு பொருட்களை வாங்க வந்தார். அங்கே அவர் தூங்கிக்கொண்டிருக்கும் அவர் குழந்தையை பார்க்கிறார்.

கணவனின் செயலால் கோபம் (Indignant) கொண்டார். சரியான பாடம் கற்பிக்க நினைத்தாள். அவன் அந்த வண்டியை வீட்டிற்கு கொண்டு சென்றார். அவன் வெளியே வந்து பார்க்கும் போது வண்டி அங்கே இல்லை.

அவன் வீட்டிற்கு சென்றான், கவலையான முகத்துடனும் நடுங்கிய (shivering) உதடுகளுடனும் மனைவி முன் நின்று குழந்தையை திருடிவிட்டார்கள் எனக் கூறினான். அவளுக்கு எப்படி எரிச்சல் (vexation) இருந்திருக்கும். இருந்தும் மதிய உணவின் சில நேரத்திற்கு முன்பு சிரித்தும் சந்தோஷப்படுத்தியும் கேட்டார்.

சரி, என் அன்பே, இன்று மதிய சாப்பாடு என்ன? அனைத்து நிகழ்வுகளையும் (குழந்தை மற்றும் நடந்த நிகழ்வுகளை) மறந்து விட்டு செயல்பட்டாள். எத்தனை ஆண்கள் ஞானிகள் விட குறைந்த மறதி மனப்பான்மை பெற்றிருப்பார்கள்? என்று நினைத்து நானும் பயப்படுகிறேன்.

புத்திசாலித்தனமாக திறமையான நினைவுகளுடன் நாம் பிறந்திருக்கிறோம், அப்படி இல்லை எனில், எந்த ஒரு நவீன நகரத்திலும் குடும்பத்தின் நிறுவனம் உயிர்வாழ முடியாது.

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th English Guide Pdf Prose Chapter 2 The Queen of Boxing Text Book Back Questions and Answers, Summary, Notes.

Tamilnadu Samacheer Kalvi 11th English Solutions Prose Chapter 2 The Queen of Boxing

11th English Guide The Queen of Boxing Text Book Back Questions and Answers

1. Antonyms:

Now, find and write the antonyms for the words in Box A from the set of words in Box B:

Question 1.
amateur
Answer:
professional

Question 2.
compulsory
Answer:
optional

Question 3.
traditional
Answer:
modern

Question 4.
expensive
Answer:
cheap

Question 5.
hopeful
Answer:
desperate

Question 6.
accepted
Answer:
refused

2. Based on your reading of the text answer the following questions in two to three sentences each:

Question a.
How did Mary Kom manage to get financial support for her trip to the USA?
Answer:
Mary Kom’s dad gave her Rs. 2,000/-. She spoke to her friend Only about her problem. He took some elders and friends to meet the two Members of Parliament and seek their support. Two MPs donated Rs, 5,000/- and 3,000/- respectively. Thus Mary Kom managed to raise a princely sum of Rs. 10,000/- for her trip to the USA.

Question b.
Why did Mary Kom think that she should not return empty-handed?
Answer:
Mary Kom thought that she should not return empty-handed as the money which the people donated for her, must not go waste.

Question c.
What was her first impression of America?
Answer:
America was cold and beautiful. What little she saw was very pleasing to her eyes. Americans were enormously nice too.

Question d.
Why did she call herself lucky?
Answer:
She did not have any match on the day of her arrival. So she called herself lucky. She was able to take enough rest to face her opponent in the round.

Question e.
According to Mary Kom, What was the reason for her loss in the finals?
Answer:
Mary Kom was not accustomed to American food. The greatest disadvantage was her loss of appetite. She could not eat food however hard she tried. She started losing weight. She was just 46 kg before the finals. This probably cost her the dream of winning the gold in the finals.

Question f.
What made her feel confident about the competitive players? Explain.
Answer:
She was the only one to win a silver medal in the competition, in spite of her weight loss. This made her feel confident about competitive players.

Question g.
What difficulty did she experience while eating Chinese food?
Answer:
Once Mary Kom and her teammates were given chopsticks to eat their food in China. Other friends, asked for spoons and managed. But Mary Kom ended up using both her hands to hold the chopsticks to pick up the food and push it into her mouth. She managed the complex work and satisfied her hunger.

Question h.
How was she felicitated on her return to India?
Answer:
She received a warm welcome and was greeted with garlands, drumbeats, and dancing in the Delhi airport. There were victory ride, thanksgiving prayers, and words of praise and felici¬tation programmes held in Langol.

Question i.
What did she consider her greatest achievement? Why?
Answer:
Mary Kom won a medal in each of the six World Boxing Championships she attended. There were a number of other international level Boxing Championships in Taiwan, Vietnam Denmark, and so on. But it was retaining her world title in 2006 by defeating Steluta Duta of Romania 22-7 at the fourth World Championship in New Delhi that she considered her greatest achievement in life because she was able to win at home.

3. Answer the following questions in a paragraph of about 100-150 words each:

Question 1.
Describe Mary Korn’s personal experiences during her first International Championship match from the time of selection to winning the medal.
Answer:
Mary Kom was selected for the Worlds Women Boxing Championship in the USA in the 48kg category. She was much worried because she did not have enough money for the trip. Her father managed to give her only a small amount. It was with the help of her friend Only. She received a princely sum as a donation from two MP s and a few more from the people. She left for the US with the thought that she could not come back empty-handed for the efforts of her people must not go waste.

When she entered Pennsylvania, she admired the beauty of it. She suffered from jet lag just because she travelled a long distance. Compared to her teammates she was lucky because she was able to take enough rest before she faced her opponent in each round. This made her won the match. She successfully entered the finals. To her bad luck, she lost her weight to 46 kg before her finals. It happened because of her loss of appetite, she lost her gold and won only a silver medal. These were her personal experiences during her first match.

Question 2.
Lack of adequate financial resources and sponsorships often affect sportspersons. How is this evident from Mary Kom’s life?
Answer:
Sports is all about Money. Mary Kom was selected to represent India in Pennsylvania, USA to contest under 48 kg World Women’s Boxing championship. Her father managed to collect only Rs. 2,000/- for her trip. Having heard of the cost of living.in USA, her heart sank. Things were very expensive in America. Her parents could do nothing more. She spoke to Onler and some of her friends. They met two local MPs and sought their help. Two MPs donated Rs. 5,000 and 3,000 respectively. It was only with the princely sum of Rs 10,000/- she was able to leave for USA.

Even after winning the first silver for India her financial worries did not end. Prize money offered respite to her immediate financial worries. She had no savings on her except a few insurance policies. She was getting married. She longed for a Government job under sports quota. With a government job she could follow her dreams with a steady income and flexible work schedule. It was only after she won her second World Women’s Boxing Championship gold, the Manipur state government offered her the job of a Sub-Inspector. Her ‘ first salary of Rs 15,000/- gave her a sense of relief.

“There is an old saying that money can’t buy happiness. If it could, I would buy myself four hits every game.”

Question 3.
Why was Mary Kom named the ‘Queen of Boxing’ and ‘Magnificent Mary?’
Answer:
Mary Kom had a good run from 2001 to 2004. She won several golds. Even after her wedding she participated in boxing and won a gold in the Third and Fourth World Women’s Boxing Championships in October 2005 and November 2006. She also won a number of other international level championships in Taiwan, Vietnam, and Denmark. Her greatest achievement was defeating Steluta Duta of Romania at the Fourth World championships in New Delhi.

It was the most memorable moment for her just because she had that victory in her home country. The other Indian boxers also performed exceptionally well. India won four golds, one silver, and three bronzes. To crown it all India won the overall title too. Thus Mary Kom had a hat-trick victory of World championship Naturally the media christened her ‘Queen of Boxing’ and ‘Magnificent Mary’.

Reading:

Encoding and Decoding:

The passage given below is on Kabbadi. Read the passage and complete the activities that follow:

Kabbadi (கபடி in Tamil) is a contact team sport that originated in Tamil Nadu, India. It is the national sport of Bangladesh. It is also popular in South Asia and is the state game of the Indian states of Tamil Nadu, Kerala, Andhra Pradesh, Bihar, Haryana, Karnataka, Maharashtra, Punjab, and Telangana.

Kabbadi is played between two teams of seven players: the objective of the game is for a single player on offence referred to as a raider, to run into the opposing teams half of a court, tag out as many of their defenders as possible, and return to their own half of the court—all without being tackled by the defenders. Points are scored for each player tagged by the raider, while the opposing team earns a point for stopping the raider.

Players are taken out of the game if they are tagged or tackled but can be ‘revived for each point scored by their team from a tag or tackle. The raider should hold his breath and utter the words like ‘kabbadi kabbadi, hututu hututu, chadu kudu’ etc. while the opponents try to catch him. If he stops uttering these words, he is considered out.

The game is known by its regional names in different parts of the subcontinent, such as Kabbadi or Chedugudu in Andhra Pradesh, Kabbadi in Kerala and Telangana, Hadudu in Bangladesh, Bhavatik in Maldives, Kauddi or Kabbadi in the Punjab Region, Hu-Tu-Tu in Western India and Hu-Do-Do in Eastern India and Chadakudu in South India. The highest governing body of Kabbadi is the International Kabbadi Federation.

Given below is the visual presentation of the first paragraph:

i) Represent the other paragraph in a visual form of your choice (flow chart, mind-map, pie-chart etc.):

ii) Choose the correct option: (Text Book Page No. 42)

Question 1.
A contact sport usually involves _______ contact between players.
a) violent
b) gentle
c) Physical
Answer:
c) Physical

Question 2.
Kabbadi is a game played between _______.
a) seven teams of two players
b) two teams of seven players
c) four teams of seven players
Answer:
b) two teams of seven players

Question 3.
A single _______.
a) Player on offence is referred to as a raider
b) offence is referred to as a raider
c) raider is an offence by the player.
Answer:
a) Player on offence is referred to as a raider

iii) Answer the following:

Question 1.
How does a raider score points for his team?
Answer:
Points are scored for each player by tagging the opponent players.

Question 2.
When does a raider concede a point to the opponent team?
Answer:
When the opposing team stops the raider it earns a point.

Question 3.
Can a player be revived when he/she is out of the game? Explain your answer?
Answer:
He can be revived for each point scored by this team from a tag or tackle.

Question 4.
Kabbadi is called by different names in different parts of India. Do you know how pallankuzhi is called in Karnataka, Andra Pradesh, and Kerala?
Answer:

• Karnataka – Aligulimane
• Andhra Pradesh – Vamana Guntalu
• Kerala – Kuzhipara

ஆசிரியரைப் பற்றி:

மாங்டே சுங்னேஜங் மேரி கோம் ஐந்து முறை குத்துச்சண்டை சேம்பியன்ஷிப் பட்டத்தை வென்ற மிகச்சிறந்த குத்துச்சண்டை வீராங்கனை. 2012ல் நடைபெற்ற ஒலிம்பிக் போட்டிகளில் வெண்கல பதக்கம் வென்றவர். இவர் பள்ளி பருவத்திலேயே வளைக்கோல்பந்து, கால்பந்து, கள விளையாட்டுகள் ஆகியவற்றில் சிறந்து விளங்கினார். சிறந்த குத்துச்சண்டை வீரரும் 1998ஆம் ஆண்டில் நடைபெற்ற ஆசிய விளையாட்டு போட்டிகளில் தங்கம் வென்றவருமான டிங்கோ சிங் என்பவரால் கவரப்பட்டு மேரிக்காம் குத்துச்சண்டை விளையாட்டை விளையாட தொடங்கினார்.

முதன்முதலில் 2001ல் அமெரிக்காவில் உள்ள பெனிசில்வேனியாவில் நடைபெற்ற சர்வதேச குத்துச்சண்டை போட்டியில் சேம்பியன் சிப் வென்ற ஒரே பெண்மணி மேரிக்காம் ஆவார். இவரின் சாதனைக்காக இந்திய அரசால் 2010ல் பத்மஸ்ரீ விருதும் 2013ல் பத்ம பூஷன் விருதும் வழங்கப்பட்டது. 2013ல் இவரின் சுயசரிதை நூலான ‘அன்பிரேக்கபுல்’ என்று நூலை எழுதினார்.

பாடத்தைப் பற்றி:
மேரிக்காம் நம் இந்திய நாட்டை சார்ந்த சிறந்த குத்துச்சண்டை வீராங்கனையாவார். 2001ம் ஆண்டில் நவம்பர் முதல் டிசம்பர் வரை நடைபெற்ற சர்வதேச குத்துச்சண்டை போட்டியில் பெண்களுக்கான 48 எடைபிரிவில் கலந்து கொண்டு வெள்ளிப்பதக்கம் பெற்றவர். அதன்பின் தன் துறையில் சாதிக்க வேண்டும் என்ற நோக்கத்தில் கடின பயிற்சி எடுத்து பல வெற்றிகளைக் கண்டார்.

இரண்டு முறை தான் கலந்து கொண்ட உலக குத்துச்சண்டை போட்டியில் தங்கம் வென்றார். இதனால் இவருக்கு உதவி காவல் ஆய்வாளராக அரசு பணி வழங்கப்பட்டடது திருமணம் ஆன பின்னும் தன் சாதனையை தொடர்ந்து கொண்டு இருக்கிறார். இவரின் சுயசரிதையில் குத்துச் சண்டையின் ராணி- மேரிகாம்” என்று குறிப்பிடப்பட்டுள்ளது. இந்த பாடம் இவரின் வாழ்வை முழுமையாய் எடுத்துக்காட்டுகிறது.

The Queen of Boxing Summary in Telugu

பாங்காங் போட்டித்தொடரை அடுத்து நான் 48 கி.கி பிரிவில் சர்வதேச குத்துச்சண்டை கழகத்தில் தேர்வு செய்யப்பட்டேன். (தொடக்கத்தில் கழகத்தின் சர்வதேச டி பாக்ஸி அமெச்சூர் அல்லது (AIBA) உலகளாவிய பெண்கள் குத்துச் சண்டை கழகம் பென்சில்வேனியா, USA, நவம்பர்-டிசம்பர் 2001 யில் நடைபெற்றது.

என் பயணத்திற்கு ரூ. 2000 மட்டுமே என் தந்தையால் ஏற்பாடு செய்ய முடிந்தது. அமெரிக்காவின் செலவீனங்களை, ஆடம்பரத்தை நினைக்கும் போது கவலையும் வருத்தமும் உண்டாகின.

ஆனால் எனது பெற்றோராலும் என்னாலும் எதையும் செய்ய இயலவில்லை. என் நண்பர் ஆன்லரிடம் என் பிரச்சனையை எடுத்துக் கூறினேன். அவன் சில மாணவர்களையும் பெரியவர்களையும் அழைத்துக் கொண்டு நாடாளுமன்றத்தில் இரு உறுப்பினர்களை சந்தித்து உதவி நாடினான்.

இரண்டு அமைச்சர்களும் தலா ரூ.5000 மற்றும் ரூ 3000 அளித்தனர். ஆகமொத்தம் என்னிடம் ரூ10,000 இருந்தது. இத்தொகை போதுமான பணம் என்று USA சென்றேன். பணம் இருப்பது எனக்கு ஆறுதல் அளித்து மக்கள் எனக்காக எடுத்த முயற்சியால் நான் வெறும் கையோடு அங்கிருந்து திரும்பி வர இயலாது.

குளிரும் அழகும் பொருந்திய நகரம் பென்சில்வேனியா. பனி பொழிந்து கொண்டிருந்தது. நாங்கள் விளையாட்டு அரங்கத்தினுள் அனுமதிக்கப்பட்டோம். அது எங்கள் கண்களுக்கு குளுமை அளித்தது. மக்கள் பேரன்புடன் பழகினர். இதுவே என் வாழ்வின் நீண்ட தூர பயணம். நானும் அமெரிக்காவை பார்த்துக்கொண்டே வந்தேன். ஆனால் எங்கள் குழு கடைசியாக வந்ததால் நேரடியாக விமான நிலையத்திலிருந்து விளையாட்டு திடலுக்கு செல்ல வேண்டியிருந்தது.

மற்ற அணி வீரர்கள் ஏற்கனவே அவர்களது எடையை சரிபார்த்தவிட்டார்கள். அது அனைத்து வீரர்களுக்கும் கட்டாயமாகும்.எனக்கு சோர்வாகவும் களைப்பாகவும் இருந்தது. நான் புறப்படும் போது காலை வேலையாக இருந்தது. இப்போது காலை வேலையாக உள்ளது. எடை சரிபார்த்த பிறகு எனக்கு இன்று போட்டிகள் இல்லை என தெரியவந்தது. ஆனால் மற்ற அணிகளுடன் இருப்பவர்களுக்கு அதிர்ஷ்டம் இல்லாமல் இருந்தது.

எனது எதிராளியை சுற்றுகளில் சந்திக்க எனக்கு நல்ல ஓய்வு கிடைத்தது, மேலும் வெல்வேன் என்ற நம்பிக்கை இருந்தது. புது எதிராளியை சந்திக்க போகிறோம் என்ற பயம் அரவே ஒழிந்தது. இந்த சேம்பியன்ஷிப் போட்டியில் 48கிலோ எடைப் பிரிவில் போட்டியிட்டேன்.

எனது அணியில் உள்ளவர்கள் ஒன்றன் பின் ஒன்றாக தோல்வியை சந்தித்தனர். ஆனால் நான் இறுதிச் சுற்றிற்கு முன்னேறினேன். தங்கம் வெல்வேன் என நம்பிக்கை வந்தது. நான் நினைத்தது போல் வீரர்கள் எளிதில் வெல்லக்கூடியவர்கள் அல்ல.

இந்த இடம் மற்றும் நடந்த நிகழ்வுகள் என் வாழ்க்கையில் மாற்றத்தை உண்டாக்கும் என உணர்ந்தேன். நான் எவரையும் காட்சியரங்கில் எதிருக்கு எதிராக சந்திப்பேன், என்று எனக்குள் சொல்லிக் கொண்டே இருந்தேன். கால் இறுதிச்சுற்றில் RSC முறையில் போலாந்தை சேர்ந்த நதியா காக்மியை வீழ்த்தினேன் (defeated-Referee stopped contest RSC நடுவர் போட்டியை நிறுத்துவது.

அதாவது போட்டியில் ஒருவர் உடல் வலிமையற்று போனால் வலிமையானவரை நடுவர் போட்டியின்றி வெற்றி பெற்றவராக அறிவிக்கலாம்). அறை இறுதியில் கனடாவின் ஜெமி பேகலை (Jamie Behal) 21-9 புள்ளிகணக்கில் வீழ்த்தி இறுதிச் சுற்றிற்கு முன்னேறினேன். ஆனால் துருகியின் குலாசாகின்டம் (Hula Sahin) 13-5 என்ற புள்ளி விகிதத்தில் தோல்வியுற்றேன்.

வென்றால் என் பசியின்மை. அங்கு உள்ள உணவை சாப்பிட நான் பழக்கப்படுத்திக் கொள்ளவில்லை. நான் முயற்சித்தாலும் என்னால் உணவு சாப்பிட முடியவில்லை. எனது எடைக் குறைந்தது. இறுதிச் சுற்றுக்கு முன்பு நான் 46 கிலோவாக குறைந்து விட்டேன். தங்கப் பதக்கம் வெல்ல வேண்டும் என்ற கனவை சிதைத்துவிட்டது. நான் என் அறைக்குச் சென்று அழுதேன்.

பயிற்சியாளர்கள் கனிவாக என்னை தேற்றி உற்சாகப்படுத்தி வெள்ளி மடல் பெறச் செய்தனர். அணியில் நான் மட்டுமே பதக்கம் பெற்றிருந்தேன். இந்த தொடர் போட்டியிலிருந்து, நான் எந்த குத்துச்சண்டை வீரரையும் எதிர் கொள்ள முடியும் என்ற முடிவுக்கு வந்தேன்.

வாழ்க்கைப் பயணங்களில் நான் பலவிதமான நாடுகள் மற்றும் இடங்களுக்குச் சென்றிருக்கிறேன். ஒரு நாள் சீனாவில் எங்களுக்கு சாப்பிட பயன்படுத்தும் குச்சி (chopsticks) உணவை சாப்பிட கொடுக்கப்பட்டது. நான் அப்போது தான் கத்தி மற்றும் முள்கரண்டி (fork) கையாலும் கலையைக் கற்றிருந்தேன்.

இரு குச்சிகளை பயன்படுத்தி என் வயிற்றை நிறைக்க வேண்டும். கடைசியில் இருகைகளால் குச்சியை வைத்து உணவை எடுத்து வாயிக்குள் தினித்தேன்.

என் அணியினர் ஸ்பூனைக் கேட்டார்கள். ஆனால் நான் குச்சியை வைத்து சமாளித்து சாப்பிட்டேன். சீன உணவின் மீது ஆர்வம் இருந்தால் அது மிகவும் உதவியது. என் பசியையும் மனதையும் திருப்திபடுத்த நான் போதுமான அளவு உண்டேன்.

ஐந்து ஆண்டுகள் பயணத்தின் பின்பு சில பதப்படுத்தப்பட்ட உணவுகளை வீட்டில் செய்து எடுத்துச் செல்லத் தொடங்கினேன். நான் டெல்லிக்கு திரும்புகையில் விமான நிலையத்தில் உற்சாக வரவேற்பு அளித்தனர்.

பூங்கொத்து, கொடுத்து மேளத் தாளங்கள், ஆட்டங்கள் என உற்சாகமாக என்னை வரவேற்றனர். வெற்றி ஊர்வலம். வரவேற்பு உரை, ஆகியவை லங்கோல் (langol) அரசு குடியிருப்பு பகுதியில் நடந்தது. பாராட்டுகளும், நன்றிகளும் என் மீது தூவப்பட்டன. கலாச்சார பொன்னாடை (shawl) Oja lbomcha என்பவரால் எனக்கு அணிவிக்கப்பட்டது. அன்று நான் லங்கோல் மக்களிடம் எதிர்காலத்தில் நான் கண்டிப்பாக தங்கம் வெல்வேன் என்று கூறினேன்.

முதல் சர்வதேச வெள்ளிப்பதக்கம் எனக்கு பல உண்மைகளை புரியவைத்தது. குத்துச் சண்டைகள் மற்றும் அதை தொடர்ந்து பல விஷயங்கள் என் மனதில் பதிவாகி உள்ளது. வெள்ளிப்பதக்கம் எனக்கு மகிழ்ச்சி தரவில்லை. நான் இந்திய மண்ணைத் தொட்டு அடுத்த முறை தங்கப் பதக்கம் வாங்குவேன் என்று சபதமெடுத்தேன். அது என்னால் முடியும் என்று எனக்குத் தெரியும்.

பென்சில்வேனியாவில் வெள்ளிப்பதக்கமும் பெற்ற பரிசுதொகையும் என்னுடைய அப்போதைய நிதிதேவையை பூர்த்தி செய்தது. நிரந்தர வருமானத்திற்கும் நீண்ட கால பாதுகாப்பிற்கும் எனக்கு ஒரு வேலை தேவைப்பட்டது. அதே சமயம் எனக்கு திருமணம் முடிந்தது. பாலிசிகள் (policies) தவிர என்னிடம் வேறு பணம் ஏதும கிடையாது.

2 வது போட்டித்தொடரில் தங்கம் வென்றேன். மனிப்பூர் அரசு எனக்கு சப்-இன்ஸ்பெக்டர் (உதவி ஆய்வாளர்) பதவியை 2005 ஆம் ஆண்டு வழங்கியது. எனது பெரிய கனவு இவ்வேளையின் மூலம் நிவர்த்தியானது. முதல் வேளையில் ரூ15,000 சம்பாதித்தேன். ஸ்போர்ட்ஸ் கொட்டா மூலம் பெறும் வேலைகளுக்கு சக ஊழியர் போல நாம் சரியாக செல்ல இயலாது. அலுவலகத்தில் உதவி தேவைப்படும் நேரம் மட்டும் செல்வேன். பெரும்பாலும் நான் விடுமுறை எடுக்க வேண்டும்.

எனது திருமணத்திற்கு பிறகும் பதக்கம் நிறைய வென்றேன். குடும்பமும், நண்பர்களும் இதைப்பற்றி பேசாத அளவிற்கு முற்றுப்புள்ளி வைத்தேன். 2005 ஆம் ஆண்டு ரஷ்யாவில் உள்ள Podolsk ல் உலக முதன்மை நிலையில் வென்றேன்.

உலகளாவிய பெண்கள் போட்டித்தொடரில் சரிதா (Sarita) வெண்கலம் வென்றாள். என்னை ஒரு hero-வைப்போல் வரவேற்றனர். Bhagyachandra திறந்த வெளி திரையரங்கில் எங்களுக்கு வரவேற்பு நடந்தது.

2001 முதல் 2004 வரை நான் அதிக புள்ளிகள் எடுத்தேன். நிறைய தங்கப்பதக்கங்கள் பெண்கள் குத்துச்சண்டை தொடரிலும், 2வது பெண்கள் குத்துச்சண்டை பிரிவு 2002, 2 வது ஆசிய குத்துச்சண்டை பிரிவில் இசார்(Hisar) 2003ல் சாம்பியன்சிப், 2013ல் ஹிசாரிலும் Hungary யில் நடைபெற்ற போட்டியிலும் சாம்பியன் சிப் பெற்றேன்.

எனது திருமணத்திற்குப் பிறகு நான் பெற்ற பதக்கங்களை பார்த்து அனைவரும் திகைத்தனர். அக்டோபர் 2005 நவம்பர் 2006 ல் நடைபெற்ற 3-வது, 4-வது உலக பெண்கள் பிரிவில் திருமணத்திற்குப் பிறகு வென்றேன்.

Vietnam, Denmark, Taiwan போன்ற நாடுகளில் பல சர்வதேச தொடர்கள் நடைபெற்றன. 2006-ல் 4 வது உலக தொடரில் ரோமானியாவின் Stelata Duta வை டெல்லியில் வென்றேன். அது என்னுடைய பெரிய வெற்றி என கருதுவேன். இது எனக்கு மறக்க முடியாத ஒன்று.

ஏனென்றால் நான் என் வீட்டில் (நாட்டில்) வெற்றி பெற முடிந்தது. இந்தியா 4 தங்கம் ஒரு வெள்ளி மற்றும் 3 வெண்கல பதக்கங்களை வென்று டைட்டிலை வென்றது. இந்த மூன்று முறை தொடர் சாதனையால் ஊடகம் என்னை குத்துச் சண்டை ராணி மகத்தான மேரி’ (Queen of Boxingand magnificent Mary) என அழைத்தது.