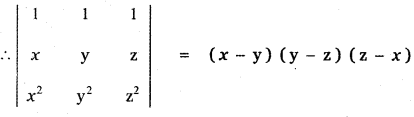Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 7 Matrices and Determinants Ex 7.3 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.3
Solve the following problems by using Factor Theorem:
![]()
Question 1.
Show that \(\left| \begin{matrix} x & a & a \\ a & x & a \\ a & a & x \end{matrix} \right| \) = (x – a)2 (x + 2a)
Answer:

By putting x = a , we have three rows of |A| are identical. Therefore (x – a)2 is a factor of |A|
Put x = – 2a in |A|
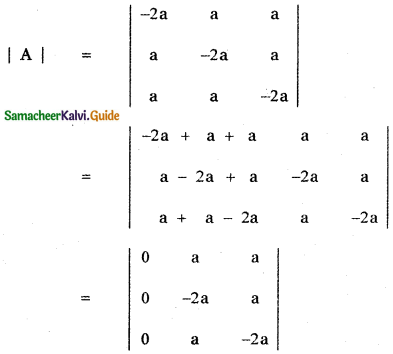
∴ x + 2a is a factor of |A|. The degree of the product of the factors (x – a)2 (x + 2a) is 3.
The degree of tfie product of the leading diagonal elements x . x . x is 3.
∴ The other factor is the contant factor k.

a3 [ – 1 (1 – 1) – 1 ( – 1 – 1) + 1 (1 + 1)] = k . 4a3
a3 [o + 2 + 2 ] = 4 ka3
4a3 = 4 ka3
k = 1
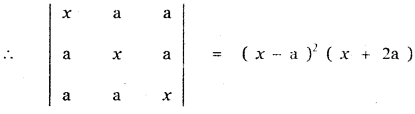
![]()
Question 2.
Show that \(\left| \begin{matrix} b\quad +\quad c & a\quad -\quad c & a\quad -\quad b \\ b\quad -\quad c & c\quad +\quad a & b\quad -\quad a \\ c\quad -\quad b & c\quad -\quad a & a\quad +\quad b \end{matrix} \right| \) = 8 abc
Answer:
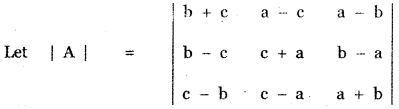
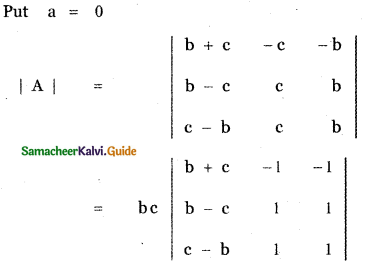
since two columns identical
= bc × 0 = 0
∴ a – 0 is a factor. That is, a is a factor.
Put b = 0 in |A|
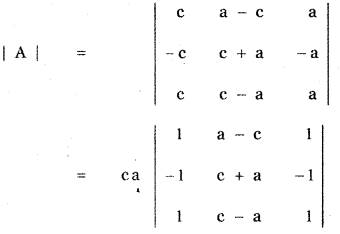
since two columns identical
= ca × 0 = 0
∴ b – 0 is a factor. That is, a is a factor.
Put c = 0 in |A|

![]()
since two columns identical
= ab × 0 = 0
∴ c – 0 is a factor. That is, c is a factor.
The degree of the product of the factors abc is 3.
The degree of the product of leading diagonal elements (b + c) (c + a) (a + b) is 3.
∴ The other factor is the constant factor k.

![]()
Question 3.
Solve that \(\left| \begin{matrix} x\quad +\quad a & b & c \\ a & x\quad +\quad b & c \\ a & b & x\quad +\quad c \end{matrix} \right| \) = 0
Answer:
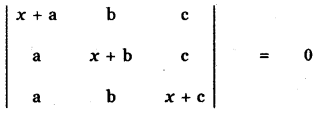
Put x = 0
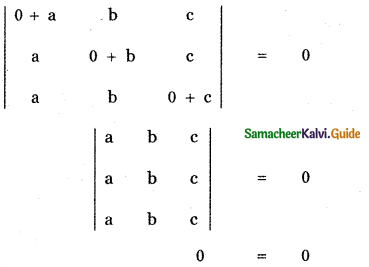
x = 0 satisfies the given equation. x = 0 is a root of the given equation, since three rows are identical. x = 0 is a root of multiplicity 2. Since the degree of the product of the leading diagonal elements (x + a) (x + b) (x + c) is 3. There is one more root for the given equation.
Put x = – (a + b + c)
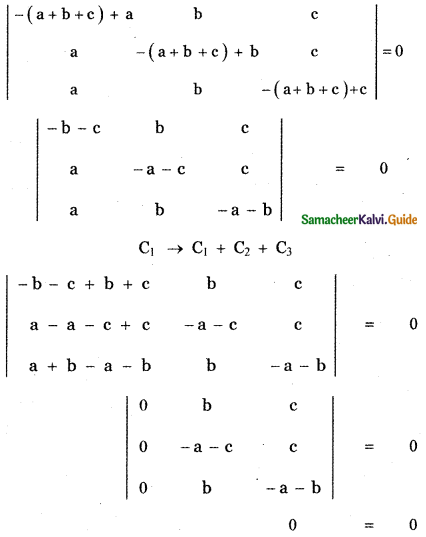
∴ x = – (a + b + c) satisfies the given equation.
Hence, the required roots of the given equation are x = 0, 0 , – (a + b + c)
![]()
Question 4.
Show that \(\left| \begin{matrix} b\quad +\quad c & a & { a }^{ 2 } \\ c\quad +\quad a & b & { b }^{ 2 } \\ a\quad +\quad b & c & { c }^{ 2 } \end{matrix} \right| \) = (a + b + c) (a – b) (b – c) (c – a)
Answer:

Since two rows are idenctical
|A| = 0
since two rows are idenctical
|A| = 0
∴ a – b is a factor of | A |. The given determinant is in cyclic symmetric form in a , b and c. Therefore, b – c and c – a are also factors. The degree of the product of the factors (a – b) (b – c) (c – a) is 3 and the degree of the product of the leading diagonal elements (b + c) . b . c2 is 4.
Therefore, the other factor is k (a + b + c).

5(18 – 12) – 1(36 – 12) + 1(12 – 6) = 12k
5 × 6 – 24 + 6 = 12k
30 – 24 + 6 = 12k
12 = 12 ⇒ k = 1
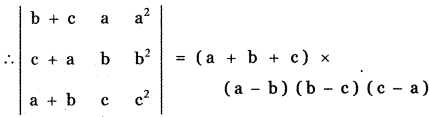
![]()
Question 5.
Solve \(\left| \begin{matrix} 4\quad -\quad x & 4\quad +\quad x & 4\quad +\quad x \\ 4\quad +\quad x & 4\quad -\quad x & 4\quad +\quad x \\ 4\quad +\quad x & 4\quad +\quad x & 4\quad -\quad x \end{matrix} \right| \) = 0
Answer:
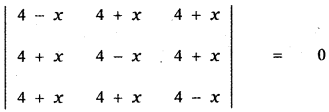
Put x = 0
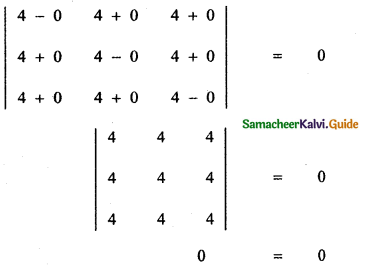
∴ x = 0 satisfies the given equation. Hence x = 0 is a root of the given equation. since three rows are identical, x = 0 is a root of multiplicity 2.
Since the degree of the product of the leading diagonal elements (4 – x) (4 – x) (4 – x) is 3. There is one more root for the given equation.

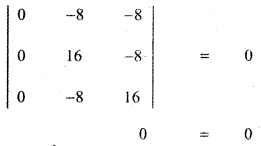
∴ x = – 12 is a root of the given equation.
Hence, the required roots are x = 0 , 0 , – 12
![]()
Question 6.
Show that \(\left| \begin{matrix} 1 & 1 & 1 \\ x & y & z \\ { x }^{ 2 } & { y }^{ 2 } & { z }^{ 2 } \end{matrix} \right| \) = (x – y) (y – z) (z – x)
Answer:

|A| = 0 since two columns identical
∴ x – y is a factor of A. The given determinant is in the cyclic symmetric form in x, y, and z. Therefore, y – z and z – x are also factors of |A|.
The degree of the product of the factors (x – y) (y – z) (z – x) is 3 and the degree of the product of the leading diagonal elements 1, y, z2 is 3. Therefore, the other factor is the constant factor k.
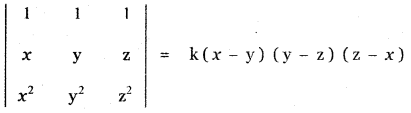
Put x = 0, y = 1, z = -1 we get
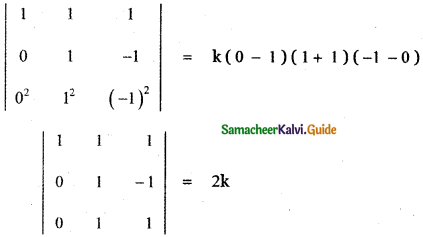
Expanding along the first column
1 (1 + 1) = 2k
2 = 2k ⇒ k = 1
![]()