Students get through the TN Board 12th Chemistry Important Questions Chapter 6 Solid State which is useful for their exam preparation.
TN State Board 12th Chemistry Important Questions Chapter 6 Solid State
Answer the following questions.
Question 1.
Why are solids rigid?
Answer:
In solids, the constituent particles (atoms, molecules, or ions) are not free to move but can only oscillate about their mean position due to strong interatomic or intermolecular forces. This imparts rigidity.
Question 2.
Classify the following as amorphous or crystalline solids.
Answer:
Polyurethane, naphthalene, benzoic acid Teflon, potassium nitrate, cellophane, polyvinyl chloride fiberglass, copper.
Amorphous solids: Polyurethane, Teflon, cellophane, polyvinyl chloride, and fiberglass. Crystalline solids: Naphthalene, benzoic acid, potassium nitrate, and copper.
Question 3.
Explain why glass is considered an amorphous solid.
Answer:
Like liquids, it has a tendency to flow, though very slowly. It does not have a sharp melting point. It is isotropic.
![]()
Question 4.
Classify the following solids in different categories based on the nature of intermolecular forces operating in potassium sulfate, tin, benzene, urea, ammonia water, zinc sulfide, graphite, rubidium, argon, silicon carbide.
Answer:
Ionic solids: potassium sulfate, zinc sulfide. Covalent solids: graphite, silicon carbide. Molecular solids: benzene, urea, ammonia water, argon.
Metallic solids: rubidium, tin.
Question 5.
Ionic solids conduct electricity in the molten state but not in the solid state. Explain.
Answer:
In ionic solids, free ions are present in a molten state and they move towards the oppositely charged electrode under the influence of electric current. In a solid state, these ions are fixed in their lattice position and cannot move under the influence of electric current.
Question 6.
Briefly outline the properties of covalent solids.
Answer:
- They have a high melting point.
- They are poor thermal and electrical conductors.
Question 7.
What are covalent solids? Give example.
Answer:
In covalent solids, the constituents (atoms) are bound together in a three-dimensional network entirely by covalent bonds. eg; Diamond, silicon carbide, etc.
Question 8.
What are molecular solids? Give examples.
Answer:
In molecular solids, the constituents are neutral molecules. They are held together by weak Van der Waals forces. Generally, molecular solids are soft and they do not conduct electricity, eg: I2, graphite.
![]()
Question 9.
Explain various types of molecular solids for example.
Answer:
Molecular solids are classified into (i) non-polar molecular solids, (ii) polar molecular solids, (iii) hydrogen-bonded molecular solids.
- In nonpolar molecular solids, the constituent molecules are held together by weak dispersion or London forces, eg: naphthalene, anthracene.
- In polar molecular solids, the constituent molecules are formed by polar covalent bonds, eg solid CO2, solid NH3.
- In hydrogen-bonded molecular solids, the constituent molecules are held together by hydrogen bonds, eg: ice (H2O), glucose, urea, etc.
Question 10.
Explain the types of the force of attraction that exist (i) nonpolar molecular solids, (ii) polar molecular solids, (iii) hydrogen-bonded molecular solids.
Answer:
- In non-polar molecular solids, the constituent particles are held together by weak dispersion or London forces.
- In polar molecular solids, the constituent molecules are held by covalent bonds. They are attracted to each other by relatively strong dipole-dipole attraction.
- In hydrogen-bonded molecular solids, the molecules are held together by hydrogen bonds.
Question 11.
What are the characteristics of metallic solids? What type of attractive forces exists among the constituent particles?
Answer:
The constituents of a metallic solid are held together by a metallic bonding. The lattice points are occupied by metals ion and the electron’s charge bond encloses the metal ion.
They are hard, possess a high melting point, They conduct heat and electricity. They possess metallic luster.
Question 12
Give examples for metallic solids.
Answer:
Metal and metal alloys, eg: Cu, Fe, Zn, Ag, Au, Cu, Zn, etc.
Question 13.
Define the following: (i) Lattice point, (ii) Crystal lattice, (iii) Unit cell.
Answer:
- Lattice point: Each lattice point represents one constituent particle of a solid. This may be an atom, molecule, or ion.
- The crystal lattice is a three-dimensional arrangement of identical points in the space which represents how the constituent particles (atoms, molecules, or ions) are arranged in a crystal.
- Unit cell A unit cell is the smallest portion of a space lattice which when repeated in different directions generates the entire lattice.
![]()
Question 14.
What are the characteristics of a unit cell?
Answer:
A unit cell is characterized by the three edge lengths or lattice constants a, b, and c and the angle between the edges α, β, and γ.
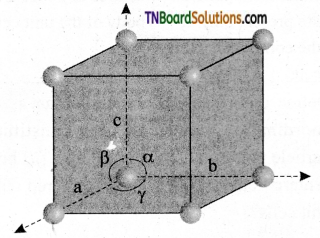
Question 15.
Briefly explain how constituent particles are arranged in (i) simple cubic, (ii) body-centered cubic, and (iii) face-centered cubic unit cells.
Answer:
- In the simple cubic unit cell, each comer is occupied by identical atoms or ions or molecules. And they touch along the edges of the cube, do not touch diagonally. The coordination number of each atom is 6.
- In a body-centered cubic unit cell, each comer is occupied by an identical particle, and in addition to that one atom occupies the body center. Those atoms which occupy the comers do not touch each other, however, they all touch the one that occupies the body center. Hence, each atom is surrounded by eight nearest neighbors and the coordination number is 8.
- In a face-centered cubic unit cell, identical atoms lie at each comer as well as in the center of each face. Those atoms in the comers touch those in the faces but not each other. The coordination number is 2.
Question 16.
Distinguish between primitive and nonprimitive unit cells.
Answer:
| Primitive unit cells | Nonprimitive unit cells |
| A unit cell that contains one lattice point is called a primitive unit cell. In a primitive unit cell, constituent particles are present only at the comers of a unit cell. | In the nonprimitive unit cells, the constituent particles are present not only at the comer but also in the centers of the face and body of the unit cell. |
Question 17.
Define coordination number? What is the coordination number of each constituent particle present at (i) simple cubic, (ii) body-centered cubic, and (iii) face-centered cubic unit cells?
Answer:
The number of constituent particles that surround an atom/ion in a crystal lattice is called the coordination number.
- The coordination number of each atom in a simple cubic unit cell is 6.
- The coordination number of each atom in a body-centered cubic unit cell is 8.
- The coordination number of an atom is a face-centered cubic unit cell is 2.
![]()
Question 18.
Explain how will you calculate the number of particles in a unit cell.
Answer:
- A point that lies at the comer of a unit cell is shared among the eight-unit cells and therefore, only one eight (\(\frac{1}{8}\)th) of each point lies within the unit cell.
- A point along the edge is shared by 4 unit cells and only \(\frac{1}{4}\)th of it lies within any one cell.
- A face-centered point is shared by 2 unit cells and only \(\frac{1}{2}\) of it is present in a given unit cell.
- A body-centered point lies entirely within the unit cell and contributes one complete point to the cell.

Total number of particles in an unit cell (z) = (\(\frac{1}{8}\) × occupied by corners) + \(\frac{1}{4}\) × (occupied by edge centres) + \(\frac{1}{2}\) × (occupied by 24 face centres) + one occupied by body centre.
Question 19.
Calculate the number of particles present in (i) simple cubic (ii) body-centered and (iii) face-centered unit cells.
Answer:
- In simple cubic unit cell particles are present only at the comers of the cube and this is shared by 8 other unit cells. Hence, the contribution of the point at the comers to the given unit cell is
∴ Z = 8 × \(\frac{1}{8}\) = 1
i.e, A simple cubic unit cell has a single constituent (atom/molecule/ion) unit per unit cell. - In the body-centered cubic unit cell, comers, as well as the center of the unit cell, are occupied.
∴ Z = 8 × \(\frac{1}{8}\) + 1 = 2
Hence body-centered cubic (bcc) has 2 constituent units per unit cell. - In face-centered cubic unit cell (fee) comers as well as face centers are occupied.
∴ Z = 8 × \(\frac{1}{8}\) + 6 + 2 = 4
Hence, the face-centered cubic unit cell has four constituent units per unit cell.
[Note: Remember that the number of atoms per unit cell is in the same ratio as the stoichiometry of the compound. Hence, it helps to predict the formula of the compound.]
![]()
Question 20.
A compound formed by elements A and B has a cubic structure in which A atoms are at the comers and B atoms are at face centers. Derive the formula of the compound.
Answer:
As ‘A’ atoms are present at the 8 comers of the cube, therefore a number of atoms of A in the unit cell = 8 × \(\frac{1}{8}\) = 1.
As ‘B’ atoms are present at the face centers of the 6 faces of the cube, therefore, the number
of atoms of B in the unit cell = \(\frac{1}{2}\) × 6 = 3.
∴ Ratio of atoms A : B = 1 : 3
∴ The formula of the compound is AB3.
Question 21.
A cubic solid is made up of two elements X and Y. Atoms ‘Y’ are present at the comers of the cube and atoms X at the body center. What is the formula of the compound? What are the coordination numbers of X and Y?
Answer:
As Y atoms are present at 8 comers, of the cube, the number of atoms of Y in the unit cell
= \(\frac{1}{8}\) × 8 = 1
As atoms X are present at the body center, therefore, the number of atoms of X in the unit cell = 1.
∴ Ratio of atoms X : Y = 1 : 1
Hence the formula of the compound is XY.
The coordination number of each X and Y = 8.
Question 22.
A compound formed by elements X and Y crystallizes in the cubic structure where Y atoms are at the comers of the cube and X atoms are at alternate faces. What is the formula of the compound?
Answer:
As there are 8 Y atoms are at the comers of the cube and the contribution of each
= \(\frac{1}{8}\) therefore no. of Y atoms per unit cell
= 8 × \(\frac{1}{8}\) = 1
These can only be 2 × atoms an alternate forces.
As contribution of each of them = \(\frac{1}{2}\).
Therefore number of X atom per unit cell
= 2 × \(\frac{1}{2}\) = 1
Ratio of atom X : Y = 1 : 1
Hence the formula of the compound is 1 : 1
Question 23.
Give the expression to find out the inter planar distance (d) between two successive planes of atoms.
Answer:
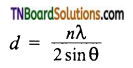
Where n is the number of planes,
λ is the wavelength of X-ray used,
θ is the angle of diffraction.
Using these values, the edge of the unit cell can be calculated.
![]()
Question 24.
X-rays of wavelength 1.54Å strike a crystal and are observed to be deflected at an angle of 22.5°. Assuming that n = 1, calculate the spacing between the planes of atoms that are responsible for this reflection.
Answer:
Applying Bragg equation,
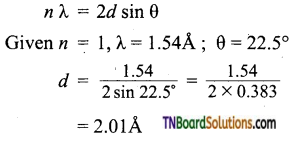
Question 25.
Derive an expression to find the density of a crystal from lattice parameters.
Answer:
Using the edge length of a unit cell, we can calculate the density (ρ) of the crystal by considering a cubic unit cell as follows.

substitute (3) in (2)
mass of the unit cell = n × \(\frac{\mathrm{M}}{\mathrm{N}_{\mathrm{A}}}\) …(4)
For a cubic unit cell, all the edge lengths are equal i.e, a = b = c
Volume of the unit cell = a × a × a = a3 …(5)

Equation (6) contains four variables namely ρ, n, M, and a. If any three variables are known, the fourth one can be calculated.
Question 26.
The edge length of a unit cell is 408 pm. Its density is 10.6 g cm-3. Predict whether the metal is body-centered, or face-centered, or simple cubic.
Answer:
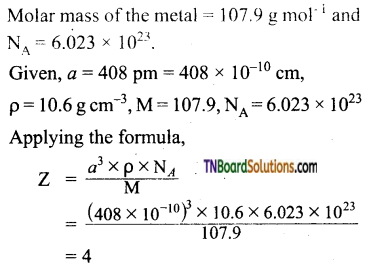
The value of Z indicates that the metal has a fee structure.
![]()
Question 27.
An element crystallizes in bcc structure the edge length of its unit cell is 288 pm. The density of the crystal is 7.2g cm-3. What is the atomic mass of the element?
Answer:

Question 28.
A metallic element exists as a body-centered cubic lattice. Each edge of the unit cell is 2.88 pm. The density of the metal is 7.2g cm-3. How many atoms and unit cells are there in 100 g of the atom?
Answer:
Let the atomic mass of the element be M.

Question 29.
The density of a face-centered cubic clement is 6.25 g cm-3. Calculate the length of the unit cell. (Atomic mass of the element = 60.2 AMU).
Answer:
Given Z = 4; M = 60.2 amu; ρ = 625 g cm-3
NA = 6.023 × 1023
Applying the formula:

![]()
Question 30.
KBr has NaCl type structure. What is the distance between K+ and Br– in KBr, if the density is 2.75 g cm-3?
Answer:
Edge length ‘a’ of the unit cell is calculated as

Question 31.
Derive an expression to calculate the packing efficiency in a simple cubic arrangement.
Answer:
Let us calculate the packing efficiency in simple cubic arrangement,
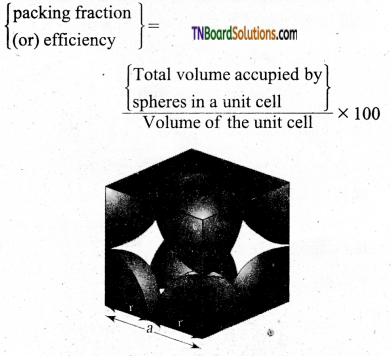
Let us consider a cube with an edge length ‘a’ as shown in fig.
Volume of the cube with edge length a is = a × a × a = a3
Let V is the radius of the sphere. From the figure, a = 2r ⇒ r = \(\frac{a}{2}\)
∴ Volume of the sphere with radius ‘r’
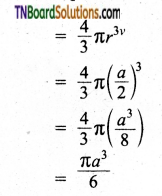
In a simple cubic arrangement, the number of spheres that belongs to a unit cell is equal to one
∴ Total volume occupied by the spheres in sc unit cell = 1 × \(\left(\frac{\pi a^{3}}{6}\right)\) ……(2)
Dividing (2) by (3)
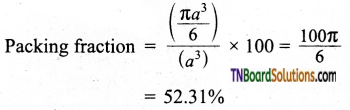
i.e., only 52.31% of the available volume is occupied by the spheres in simple cubic packing, making inefficient use of available space and hence minimizing the attractive forces.
![]()
Question 32.
Show that the packing efficiency in the face-centered cubic unit cells is 74%.
Answer:
The cubic close packing is based on the face-centered cubic unit cell. Let us calculate the packing efficiency in the fcc unit cell.
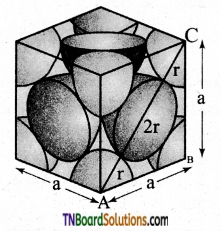

The total number of spheres belongs to a single fcc unit cell is 4

Question 33.
Give the relationship between the nearest neighbor distance (d) and the edge (a) of the unit cell of a cubic crystal.
Answer:
For simple cubic: d = a
For face centered cubic: d = \(\frac{a}{\sqrt{2}}\) = 0.707a
For body centered cubic:
d = \(\frac{\sqrt{3}}{2} a\)
![]()
Question 34.
Give the relationship between atomic radius (r), (which is d/2 for crystals of pure substances) and edge (a) of the unit cell of a cubic crystal.
Answer:
For simple cubic: r = \(\frac{a}{2}\)

Question 35.
Xenon crystallizes in face-centered cubic lattice and the edge of the unit cell is 620 pm. What is the nearest neighbor distance and what is the radius of the xenon atom?
Answer:
Here, a = 620 pm; d = 2 ; r = ?

Question 36.
CsCl has bcc arrangement and its unit cell edge length is 400 pm. Calculate the interionic distance in CsCl.
Answer:
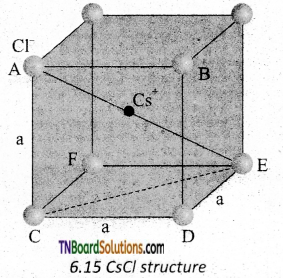
The bcc arrangement of CsCl is shown in fig. Where black circle is Cs+ ion and colored circles are Cl– ions. The aim is to find half of the body diagonal AE. If the edge of the unit cell is ‘a’.

Question 37.
If the radius of the atom is 75 pm and the lattice type is body-centered cubic, what is the edge of the unit cell?
Answer:
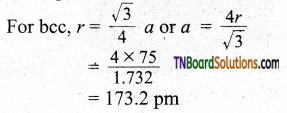
![]()
Question 38.
The radius of an atom of an element is 500 pm. If it crystallizes as fee lattice, what is the length of the side of the unit cell?
Answer:
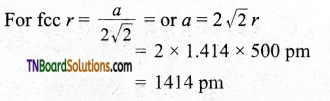
Question 39.
A solid AB has a CsCl type structure. The edge length of the unit cell is 404 pm. Calculate the distance of the closest approach between A+ / B– ions.
Answer:
The distance of the closest approach is equal to the distance between nearest neighbors (d). As CsCl has a bcc lattice.
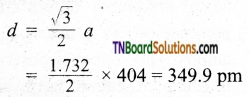
Question 40.
What is the radius ratio? Mention its importance.
Answer:
In ionic solids, the ratio of the radius of the cation to the radius of an anion is known as the radius ratio.
![]()
The radius ratio of an ionic solid gives the structural arrangement of ionic solids.
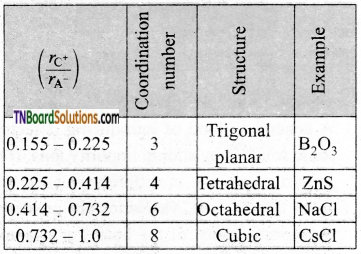
Question 41.
What is the meaning of the term imperfection in solids?
Answer:
Imperfection refers to the departure from the perfect periodic arrangement of atoms, ions, or molecules in the structure of crystalline solids.
Question 42.
What are the types of lattice imperfections found in crystals?
Answer:
- Stoichiometric defect i.e., Schottky defect and Frenkel defect.
- Nonstoichiometric defect viz metal excess, metal deficiency, and impurity defects.
![]()
Question 43.
What are interstitials in a crystal?
Answer:
Atoms or ions that fill the normal vacant interstitial voids in a crystal are known as interstitials.
Question 44.
What is the Schottky defect?
Answer:
If an equal number of cations and anions are missing from their lattice sites, the defect is known as the Schottky defect.
Question 45.
What is Frenkel’s defect?
Answer:
When some ions (usual cation) are missing from the lattice sites and they occupy the interstitial sites. So that, the electro-neutrality, as well as stoichiometry are maintained, it is called Frenkel defect.
Question 46.
Which crystal defect lowers the density of the solid?
Answer:
Schottky defect.
Question 47.
Which crystal defect in crystals does not alter the density of a relevant solid?
Answer:
Frenkel defect.
Question 48.
Which point does defect increase the density of the solid?
Answer:
Schottky defect.
![]()
Question 49.
Which point defect in the crystal increases the density of the solid?
Answer:
Interstitial defect.
Question 50.
Name one solid in which both Frenkel and Schottky defects occur.
Answer:
Silver Bromide.
Question 51.
Why does the Frenkel defect does not change the density of AgCl crystal?
Answer:
Because in Frenkel defect, no ion is missing from the lattice sites. Therefore, no change in density occurs.
Question 52.
What are F. Centres?
Answer:
The free-electron trapped in the anion vacancy is called F.Centres.
Question 53.
What are non-stoichiometric defects?
Answer:
If as a result of imperfections in the crystal, the ratio of the cation to the anions becomes different from that indicated by their ideal chemical formula, then the defect is termed a non-stoichiometric defect.
Question 54.
Why does table salt, NaCl appear yellow in color?
Answer:
Yellow color in sodium chloride is due to metal excess defect due to which unpaired electrons occupy anionic sites. These sites are called F. Centres. These electrons absorb energy from the visible region for excitation which makes the crystal yellow.
![]()
Question 55.
Why is FeO (s) not formed in stoichiometric composition?
Answer:
In the crystal of FeO, some of Fe+2 cations are replaced by Fe+3 cations. Three Fe+2 cations are replaced by two Fe+3 cations to make up for the loss of positive charge. Eventually, there would be fewer atoms of the metal as compared to stoichiometric proportion.
Question 56.
How would you account for the following?
- Frenkel defects are not found in alkali metal halides.
- Schottky defects lower the density of the solid.
- Impurity doped silicon is a semiconductor.
Answer:
- This is because alkali metal ions have larger sizes that cannot fit into interstitial sites.
- As the number of ions decreases as a result of the Schottky defect, the mass decreases whereas the volume remains the same.
- This is due to additional electrons or the creation of holes and doping with impurity. Creation of hole results in p-type semiconductor and creation of electron results in the n-type semiconductor.
Question 57.
Briefly explain the metal excess defect.
Answer:
The metal excess defect arises due to the presence of more metal ions as compared to anions. Alkali metal halides NaCl, KCl show this type of defect. The electrical neutrality of the crystal can be maintained by the presence of anionic vacancies equal to the excess metal ions (or) by the presence of extra cation and electrons present in the interstitial position.
![]()
Question 58.
Briefly explain metal deficiency defects.
Answer:
Metal deficiency defect arises due to the presence of fewer cations than the anions. This defect is observed in a crystal in which, the cations have variable oxidation states.
Question 59.
Briefly explain the impurity defect.
Answer:
A general method of introducing defects in ionic solids is by adding impurity ions. If the impurity ions are in a different valance states from that of the host, vacancies are created in the crystal lattice of the host. For example, the addition of CdCl2 to silver chloride yields solid solutions where the divalent cation Cd2+ occupies the position of Ag+. This will disturb the electrical neutrality of the crystal. In order to maintain the same, a proportional number of Ag+ ions leaves the lattice. This produces a cation vacancy in the lattice, such kinds of crystal defects are called impurity defects.
Choose the correct answer.
1. Which one of the following is a covalent crystal?
(a) Rock salt
(b) Ice
(c) Quartz
(d) Dry ice
Answer: (c)
Hint: Rock salt is an ionic solid, while dry ice and ice are molecular solids.
2. Total volume of atoms present in a face centered cubic unit cell of a metal is:
(r = atomic radius)

Answer: (b)
Hint: Total no. of atoms in fee unit cell = 4
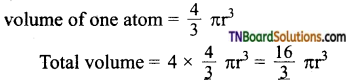
![]()
3. The fraction of the total volume occupied by the atoms present in a simple cube is:

Answer: (b)
In a simple cube, no. of atoms / unit cell = 8 × \(\frac{1}{8}\) = 1

4. Three elements A, B and C crystallise into a cubic solid lattice. Atoms A occupies the comers, B atoms, the cubic centres, and atoms C, the edges. The formula of the compound is:
(a) ABC
(b) ABC2
(c) ABC3
(d) ABC4
Answer: (c)
Hint:
Atoms A per unit cell = 8 × \(\frac{1}{8}\) = 1
Atom B per unit cell = 1
Atoms C per unit cell = 12 × \(\frac{1}{4}\) = 3
Ratio A : B : C = 1 : 1 : 3.
Hence the formula is ABC3.
5. An alloy of copper, silver and gold is found to have copper forming the simple cubic close packed lattice. If silver atoms occupy the comers and gold atoms are present at the body centres, the formula of the alloy will be:
(a) Cu3 Ag Au
(b) Cu Ag3 Au
(c) Cu4 Ag2 Au
(d) Cu Ag Au.
Answer: (b)
Hint:
Cu atoms per unit cell (present at the comer) = 8 × \(\frac{1}{8}\) = 1
Ag atoms per unit cell (present at the face centres) = 6 × \(\frac{1}{2}\) = 3
Au atoms per unit cell (present at body centre) = 1
Hence the formula is Cu Ag3 Au.
![]()
6. A solid compound XY has NaCl structure. If the radius of the cation is 100 pm, the radius of the anion (Y–) will be:
(a) 275.1 pm
(b) 322.5 pm
(c) 241.5 pm
(d) 165.7 pm
Answer: (c)
Hint: NaCl has a face centered cubic structure. Cl– ions and Na+ ions are present in the octahedral voids. Hence for such a solid, radius of the cation is = 0.414 × radius of the anion.

7. The number of atoms in 100g of the fcc crystal with density = 10 g/cm3, and the cell edge equal to 200 pm is equal to:
(a) 5 × 1024
(b) 5 × 1025
(c) 6 × 1023
(d) 2 × 1025
Answer:
(a)
Hint:

Thus 12g of the atom contain = 6.023 × 1023 atom.
∴ 100g of the atom will contain
![]()
8. Which of the following statements is not true about amorphous solids?
(a) On heating they may become crystalline at certain temperature.
(b) They may become crystalline or keeping for long time.
(c) Amorphous solids can be moulded by heating.
(d) They are anisotropic in nature.
Answer:
(d)
![]()
9. The sharp melting point of crystalline solids is due to:
(a) a regular arrangement of constituent particles observed over a short distance in the crystal lattice.
(b) a regular arrangement of constituent particles observed over a long distance in the crystal lattice.
(c) same arrangement of constituent particles in different directions.
(d) different arrangement of constituent particles in different directions.
Answer:
(b)
10. Iodine molecules are held in the crystal lattice by:
(a) London forces
(b) dipole – dipole interaction
(c) covalent bonds
(d) columbic forces
Answer:
(a)
11. Which of the following is a network solid?
(a) SO2 (solid)
(b) I2
(c) diamond
(d) H2O (ice)
Answer:
(c)
12. Which of the following solids is not an electrical conductor?
(i) Mg(s)
(ii) TiO(s)
(iii) I2 (s)
(iv) H2O (ice)
(a) (i) only
(b) (ii) only
(c) (iii) and (iv)
(d) (ii), (iii) and (iv)
Answer:
(c)
![]()
13. The lattice sites in a pure crystal cannot be occupied by:
(a) molecule
(b) ion
(c) electron
(d) atom
Answer:
(c)
Hint: Electrons can occupy only in the interstitial sites.
14. Cations are present in interstitial sites in:
(a) Frankel defect
(b) Schottky defect
(c) Valency defect
(d) Metal deficiency defect
Answer:
(a)
15. Schottky defect is obtained in crystal when:
(a) Some cations move from their lattice sites to interstitial sites.
(b) equal number of cations and anions are missing from the lattice.
(c) Some lattice sites are occupied by electrons.
(d) Some impurity is present in the lattice.
Answer:
(b)
16. The total number of tetrahedral void in the face centered unit cell is:
(a) 6
(b) 8
(c) 10
(d) 12
Answer:
(b)
Hint: No. of atoms per unit cell in fee = 4
No. of tetrahedral void: 2 × 4 = 8.
![]()
17. Which of the following statements is not true about hexagonal close packing?
(a) The coordination number is 12.
(b) It has 74% packing efficiency.
(c) Tetrahedral voids of the second layer are covered by spheres of the third layer.
(d) In this arrangement spheres of the fourth layer are exactly aligned with those of the first.
Answer: (d)
Hint: In hcp arrangement ABAB type and not ABC ABC type. Hence (d) is not true.
18. What is the coordination number in square close packed structure in two dimensions?
(a) 2
(b) 3
(c) 4
(d) 6
Answer:
(c)
Hint: The arrangement is AA AA type. In this arrangement each sphere is touching four other spheres touching the particular sphere, a square is formed. Hence, the coordination number is 4.
19. The correct order to packing efficiency in different type of unit cells is:
(a) fee < bee < simple cubic
(b) fee > bcc > simple cubic
(c) fee < bcc > simple cubic
(d) bcc < fee > simple cubic
Answer:
(b)
Hint: fcc = 74%, bcc = 68%; simple cubic = 52.4%
20. In cubic close packing, the unit cell has:
(a) 4 tetrahedral voids each of which is shared by adjacent unit cells. .
(b) 4 tetrahedral voids within the unit cell.
(c) 8 tetrahedral voids each of which is shared by four adjacent unit cells.
(d) 8 tetrahedral voids within the unit cells.
Answer:
(d)
Hint: ccp = hcp
No. of atoms per unit cell in fcc unit cell = 4.
∴ No. of tetrahedral voids = 2 × 4 = 8
![]()
21. KCl crystallises in the same type of lattice as does NaCl.
Given that \(r_{\mathrm{Na}^{+}} / r_{\mathrm{Cl}^{-}}\) is 0.55 and \(r_{\mathrm{K}^{+}} / r_{\mathrm{Cl}^{-}}\) is 0.74, Calculate the ratio of the side of the unit cell of KCl and NaCl.
(a) 1.123
(b) 0.891
(c) 1.414
(d) 0.414
Answer:
(a)

22. Ice crystallises in a hexagonal lattice having a volume of the unit cell is 132 × 10 cm3. It density of ice at the given temperature is 0.92 g cm-3, then number of H2O molecules per unit cell is:
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d)
Hint:

![]()
24. The edge length of the face-centered cubic unit cell is 508 pm. If the radius of the cation is 110 pm, the radius of the anion will be:
(a) 144 pm
(b) 288 pm
(c) 618 pm
(d) 398 pm
Answer:
(a)
Hint: For the face-centered cubic unit cell (eg: NaCl),
the edge length = 2 × distance between cation and anion
= 2 (r+ + r–)
2(r+ + r–) = 508 pm
given r+ = 110 pm
2(110 + r–) = 508 pm
r– = 144 pm
25. Which of the following statements is not correct?
(a) The fraction of the total volume occupied by the atoms in a primitive cell is 0.48
(b) Molecular solids are generally volatile.
(c) The number of carbon atoms in a unit cell of a diamond is 4.
(d) The number of brave lattices in which a crystal can be categorized it.
Answer:
(c)
26. Match the entities with a column I with appropriate entities in column II and choose the correct option using the code given.
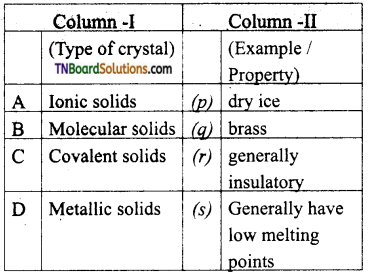
(a) (A) – r; (B) – p, r, s; (C) – r, (D) – q
(b) (A) – p,r; (B) – s; (C) – r; (D) – q
(c) (A) – r; (B) – p,s; (C) – q; (D) – r
(d) (A) – r, (B) – s; (C) – r; (D) – p
Answer:
(a)
![]()
27. Match the entities with column I with appropriate entities in column II and choose the correct option using the code given.
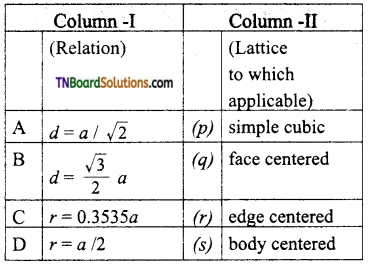
a = cell edge
d = nearest neighbour distance
r = radius
(a) (A) – q; (B) – r; (C) – p; (D) – s
(b) (A) – q; (B) – p; (C) – r; (D) – 5
(c) (A) – q; (B) – s; (C) – q; (D) – p
(d) (A) – q; (B) – s; (C) – r; (D) – p
Answer:
(c)
28. Match the entities with column I with appropriate entities in column II and choose the correct option using the code given.
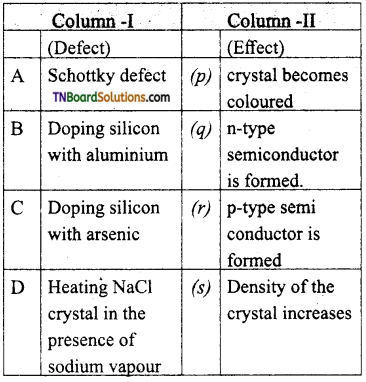
(a) (A) – s; (B) – q; (C) – r; (D)-p
(b) (A) – q; (B) – p; (C) – r; (D) – s
(c) (A) – r; (B) – s; (C) – q; (D) – p
(d) (A) – s; (B) – r; (C) – p; (D) – q
Answer:
(a)
![]()
29. Assertion (A): Hexagonal close packing is more closely packed than cubic close packing.
Reason (R): Hexagonal close-packing has a coordination number 12 whereas the cubic close packing has a coordination number 8.
(a) If both assertion and reason are true and the reason is the correct explanation of assertion.
(b) If both assertion and reason are true, and the reason is not the correct explanation of assertion.
(c) If the assertion is true but the reason is false.
(d) If both assertion and reason are false.
Answer:
(d)
Hint:
Correct assertion: Hexagonal close packing and cubic close packing are equally close-packed with a packing efficiency of 74%.
Correct reason: Both have the coordination number 12.
30. Assertion (A): Frankel defects are shown by silver halides.
Reason (R): Ag+ ion is smaller in size.
(a) If both assertion and reason are true and the reason is the correct explanation of assertion.
(b) If both assertion and reason are true, and reason is not the correct explanation of assertion.
(c) If the assertion is true but the reason is false.
(d) If both assertion and reason are false.
Answer:
(a)