Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 9 Applications of Integration Ex 9.3 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.3
Question 1.
Evaluate the following definite integrals.
(i) \(\int_{3}^{4}\) \(\frac{dx}{x^2-4}\)
Solution:
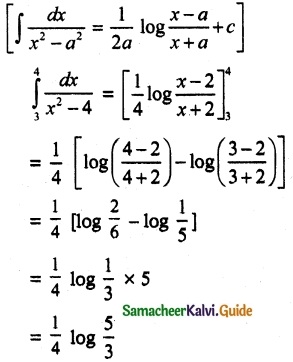
![]()
(ii) \(\int_{-1}^{1}\) \(\frac{dx}{x^2+2x+5}\)
Solution:
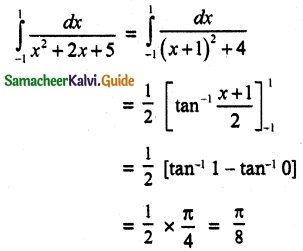
(iii) \(\int_{0}^{1}\) \(\frac{\sqrt{1-x}}{\sqrt{1+x}}\) dx
Solution:

![]()
(iv) \(\int_{0}^{\pi / 2}\) (\(\frac{1+sin}{1+cosx}\))dx
Solution:

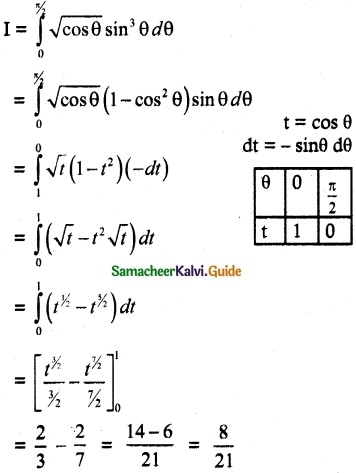
(v) \(\int_{0}^{\pi / 2}\) \(\sqrt{cos θ}\) sin³θ dθ
Solution:
![]()
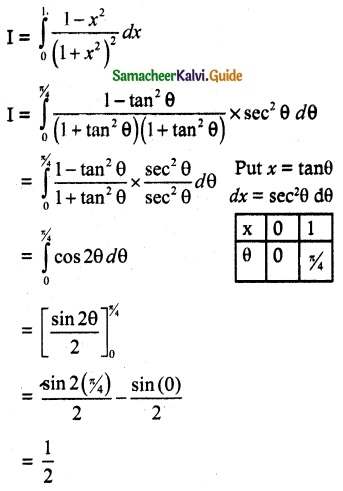
(vi) \(\int_{0}^{1}\) \(\frac{1-x^2}{(1+x^2)^2}\) dx
Solution:
Question 2.
Evaluate the following integrals using properties of integration:
(i) \(\int_{-5}^{5}\) x cos (\(\frac{e^x-1}{e^x+1}\)) dx
Solution:

![]()
(ii) \(\int_{-\pi / 2}^{\pi / 2}\) (x5 + x cos x + tan³ x) dx
Solution:
\(\int_{-\pi / 2}^{\pi / 2}\) (x5 + x cos x + tan³ x) dx
= \(\int_{-\pi / 2}^{\pi / 2}\) (x5 + x cos x + tan³ x) dx + \(\int_{-\pi / 2}^{\pi / 2}\)
Let f(x) = x5 + x cos x + tan³x
f(-x) = -x5 – x cos x – tan³x
f(x) = -f(-x)
f(x) is an odd function
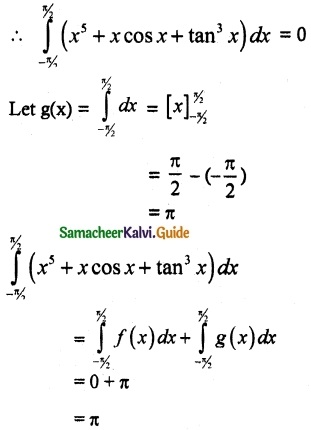
(iii) \(\int_{-\pi / 4}^{\pi / 4}\) sin² x dx
Solution:
I = \(\int_{-\pi / 4}^{\pi / 4}\) sin² x dx
f(x) = sin²x
f(-x) = sin²(-x) = sin²x
f(x) = f(-x)
f(x) is an even function
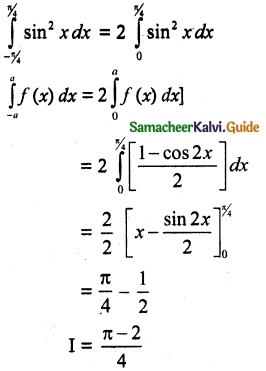
![]()
(iv) \(\int_{0}^{2π}\) x log(\(\frac{3+cos x}{3-cos x}\))dx
Solution:
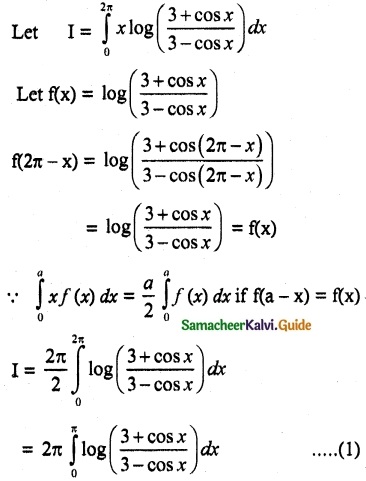
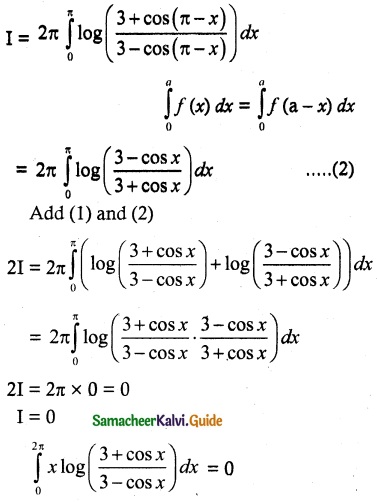
(v) \(\int_{0}^{π}\) sin4 x cos³ x dx
Solution:
\(\int_{0}^{π}\) sin4 x cos³ x dx
f(x) = sin4x cos³x
f(2π – x) = sin4(2π – x) cos³ (2π – x)
= sin4x cos³x
f(2π – x) = f(x)
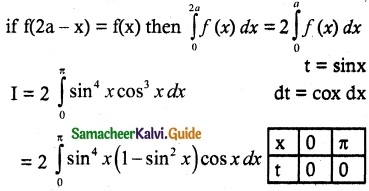
Limit from 0 to π tends to 0 to 0
∴ Integral value = 0
∴ \(\int_{0}^{π}\) sin4 x cos³ x dx = 0
![]()
(vi) \(\int_{0}^{1}\) |5x – 3|dx
Solution:
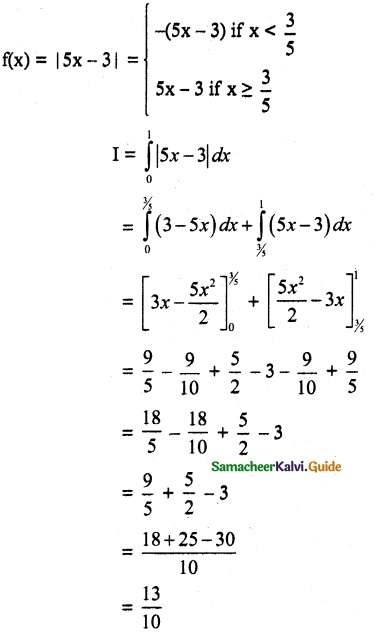
(vii) \(\int_{0}^{sin^2x}\) sin-1 √t dt + \(\int_{0}^{cos^2x}\) cos-1 √t dt
Solution:
I1 = \(\int_{0}^{sin^2x}\) sin-1 √t dt
Put sin-1 √t = θ
√t = sin θ
\(\frac{1}{2√t}\) dt = cos θ dθ
dt = 2√t cos θ dθ
= 2 sin θ cos θ dθ
dt = sin 2θ dθ
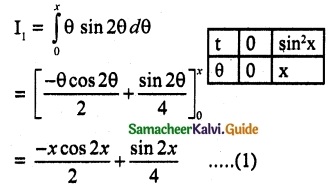
I1 = \(\int_{0}^{cos^2x}\) cos-1 √t dt
Put cos-1 √t = θ
√t = cos θ
\(\frac{1}{2√t}\) dt = -sin θ dθ
dt = -2√t sin θ dθ
= -2 cos θ sin θ dθ
dt = -sin 2θ dθ
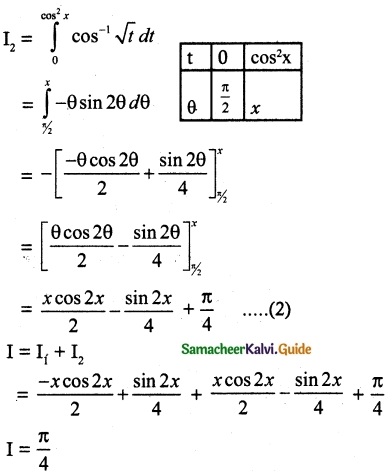
![]()
(viii) \(\int_{0}^{1}\) \(\frac{log(1+x)}{1+x^2}\) dx
Solution:

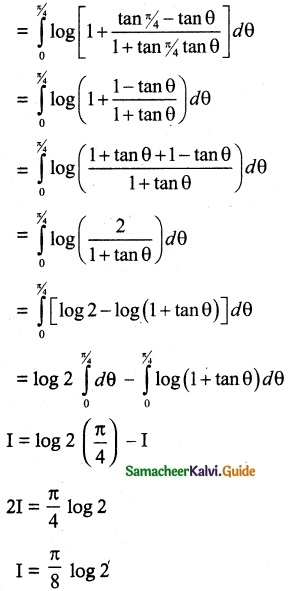
(ix) \(\int_{0}^{π}\) \(\frac{x sin x}{1+sin x}\) dx
Solution:
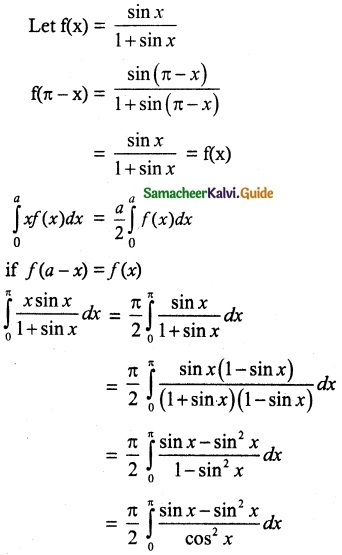
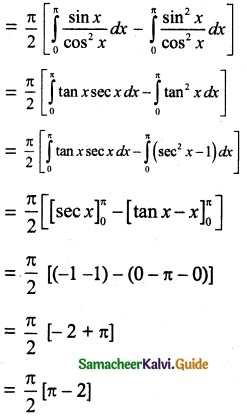
![]()
(x) \(\int_{π/8}^{3π/8}\) \(\frac{1}{1+\sqrt{tan x}}\) dx
Solution:

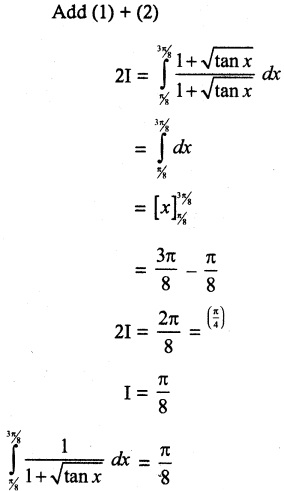
![]()
(xi) \(\int_{0}^{π}\) x[sin²(sin x) + cos² (cos x)] dx
Solution:
Let I = \(\int_{0}^{π}\) x[sin²(sin x) + cos² (cos x)] dx
f(x) = sin² (sin x) + cos² (cos x)
f(π – x) = sin² (sin π – x)) + cos² (cos(π – x))
= sin² (sin x) + cos² (cos x)
f(x) = f(π – x)
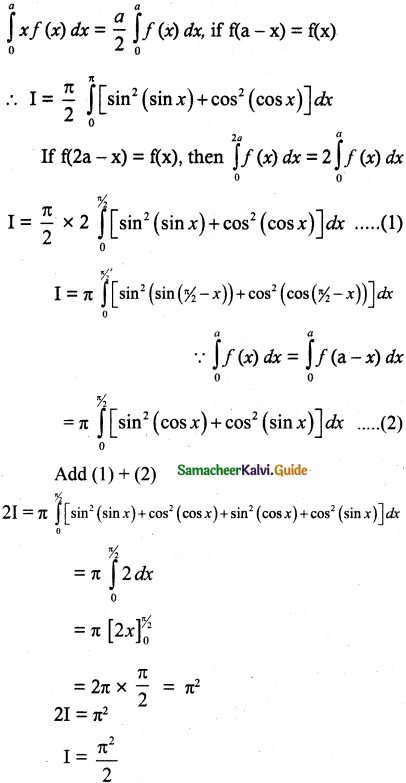
![]()