Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 8 Differentials and Partial Derivatives Ex 8.3 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.3
Question 1.
Evaluate \(\lim _{(x, y) \rightarrow(1,2)}\) g(x, y), if the limit exists where g(x, y) = \(\frac { 3x^2-xy }{ x^2+y^2+3 }\)
Solution:
\(\lim _{(x, y) \rightarrow(1,2)}\) g(x, y) = \(\lim _{(x, y) \rightarrow(1,2)}\) \(\frac { 3x^2-xy }{ x^2+y^2+3 }\)
= \(\frac { 3(1)-1×2 }{ 1+4+3 }\)
= \(\frac { 1 }{ 8 }\)
![]()
Question 2.
Evaluate \(\lim _{(x, y) \rightarrow(0,0)}\) cos(\(\frac { x^3+y^2 }{ x+y+2 }\)), if the limit exists.
Solution:
\(\lim _{(x, y) \rightarrow(0,0)}\) cos(\(\frac { x^3+y^2 }{ x+y+2 }\))
= cos (\(\frac { 0+0 }{ 0+0+2 }\))
= cos 0
= \(\lim _{(x, y) \rightarrow(0,0)}\) cos(\(\frac { x^3+y^2 }{ x+y+2 }\)) = 1
Question 3.
Let f(x, y) \(\frac { y^2-xy }{ √x-√y }\) for (x, y) ≠ (0, 0) show that \(\lim _{(x, y) \rightarrow(0,0)}\) f(x, y) = 0
Solution:
f(x, y) = \(\frac { y^2-xy }{ √x-√y }\)

![]()
Question 4.
Evaluate \(\lim _{(x, y) \rightarrow(0,0)}\) cos(\(\frac { e^xsin y }{ y }\)), if the limit exists.
Solution:
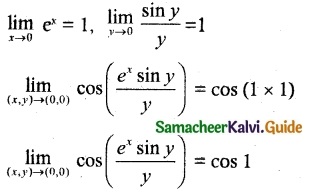
Question 5.
Let g(x, y) = \(\frac { x^2y }{ x^4+y^2 }\) for (x, y) ≠ (0, 0) and f(0, 0) = 0
(i) Show that \(\lim _{(x, y) \rightarrow(0,0)}\) g(x, y) = 0 along every line y = mx, m ∈ R
(ii) Show that \(\lim _{(x, y) \rightarrow(0,0)}\) g(x, y) = \(\frac { k }{ 1+k^2 }\) along every parabola y = kx², k ∈ R\{0}
Solution:
(i) Let g(x, y) = \(\frac { x^2y }{ x^4+y^2 }\) for (x, y) ≠ (0, 0) and f(0, 0) = 0
Let y = mx
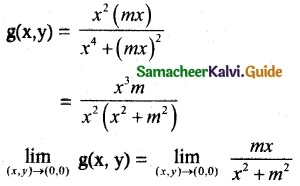
= 0
Hence proved
(ii) for parabola y = kx²

Hence proved
![]()
Question 6.
Show that f (x, y) = \(\frac { x^2-y^2 }{ y^+1 }\) is continuous at every (x, y) ∈ R²
Solution:
Let (a, b) ∈ R² be an arbitrary point.
We shall investigate the continuity of f at (a,b).
That is, we shall check if all the three conditions for continuity hold for f at (a, b)
To check first condition, note that
f(a, b) = \(\frac { a^2-b^2 }{ b^2+1 }\) is defined
Next we want t0 find lf \(\lim _{(x, y) \rightarrow(a,b)}\) f(x, y) exist or not
so we calculate \(\lim _{(x, y) \rightarrow(a,b)}\) x² – y² = a² – b² and
\(\lim _{(x, y) \rightarrow(a,b)}\) y² + 1 = b² + 1
By the properties of limit we see that
\(\lim _{(x, y) \rightarrow(a,b)}\) f(x, y) = \(\frac { x^2-y^2 }{ y^2+1 }\) = \(\frac { a^2-b^2 }{ b^2+1 }\) = f(a, b) = L exists
Now, we note that \(\lim _{(x, y) \rightarrow(a,b)}\) f(x, y) = L = f(a, b).
Hence f satisfies all the there conditions for continuity of f at (a, b).
Since (a, b) is an arbitrary point in R², we conclude that f is continuous at every point of R².
![]()
Question 7.
Let g (x, y) = \(\frac { e^ysinx }{ x }\) for x ≠ 0 and g(0, 0) = 1 shoe that g is continuous at (0, 0)
Solution:
g(x, y) = \(\frac { e^ysinx }{ x }\)
To check first condition,note that
\(\lim _{(x, y) \rightarrow(0,0)}\) g(x, y) = \(\lim _{(x, y) \rightarrow(0,0)}\) \(\frac { e^ysinx }{ x }\) = 1 is defined
Next \(\lim _{(x, y) \rightarrow(0,0)}\) g(x, y) = \(\frac { e^ysinx }{ x }\) = 1 = L Exist
Now we note \(\lim _{(x, y) \rightarrow(0,0)}\) g(x, y) = L = g(0, 0)
Hence g satisfies all the three conditions for; continuity of g at (0, 0).
We conclude that g is continuous at (0, 0).
![]()