Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 Applications of Differential Calculus Ex 7.9 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.9
Question 1.
Find the asymptotes of the following curves:
(i) f(x) = \(\frac { x^2 }{ x^2-1 }\)
(ii) f(x) = \(\frac { x^2 }{ x+1 }\)
(iii) f(x) = \(\frac { 3x }{ \sqrt{x^2+2} }\)
(iv) f(x) = \(\frac { x^2-6x-1 }{ x+3 }\)
(v) f(x) = \(\frac { x^2+6x-4 }{ 3x-6 }\)
Solution:
(i) f(x) = \(\frac { x^2 }{ x^2-1 }\)
The function becomes undefined when x = 1 and x = -1
∴ x = 1 and x = -1 are the vertical asymptotes
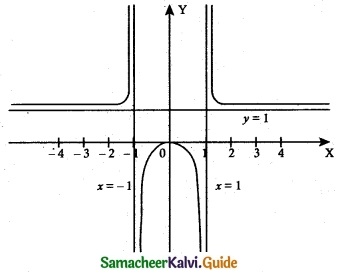
As ‘x’ gets larger (Positive or negative) the function, the function attaining the value 1.
∴ y = 1 is horizontal asymptote
![]()
(ii) f(x) = \(\frac { x^2 }{ x+1 }\)
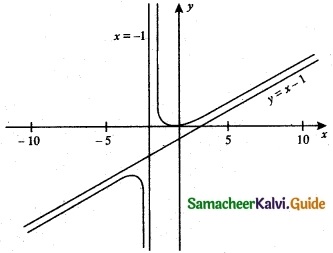
The function becomes undefined when x = -1
∴ Vertical asymptote is x = -1 and there is no horizontal asymptote.
No horizontal asymptote exists for the curve. Oblique asymptote can be obtained by polynomial long division method.
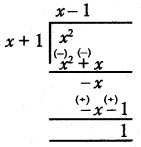
Oblique (or) slant asymptote is y = x – 1
![]()
(iii) f(x) = \(\frac { 3x }{ \sqrt{x^2+2} }\)
No vertical asymptotes
Horizontal asymptotes RHL (Right Hand Limit)
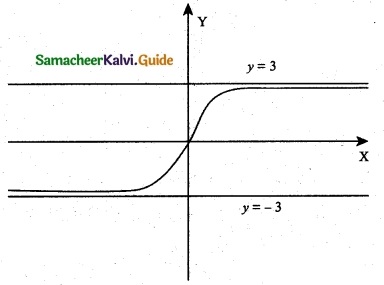

y = 3 and y = -3 are the Horizontal asymptotes
Slant asymptotes’. No such slant asymptotes exist for the given curve.
![]()
(iv) f(x) = \(\frac { x^2-6x-1 }{ x+3 }\)
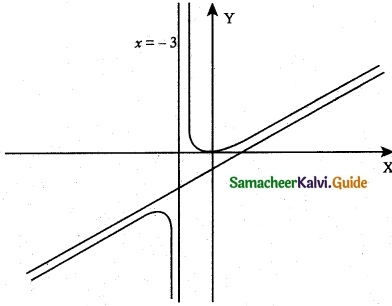
When x = -3, the function becomes undefined.
∴ x = -3 is the vertical asymptote.
No Horizontal asymptote exist for the curve.
Oblique asymptote can be obtained by polynomial long division method
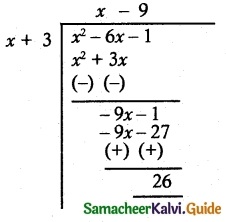
∴ y = x – 9 is the slant (or) oblique asymptote.
![]()
(v) f(x) = \(\frac { x^2+6x-4 }{ 3x-6 }\)
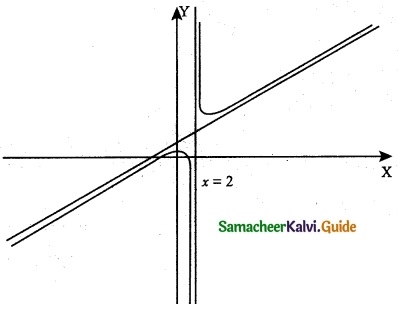
The function becomes undefined when x = 2.
∴ x = 2 is the vertical asymptote.
No Horizontal asymptote exist for the given curve.
Oblique asymptote can be obtained by polynomial long division method.
∴ y = \(\frac { x }{ 3 }\) + \(\frac { 8 }{ 3 }\) (or) 3y = x + 8 is the slant asymptote.
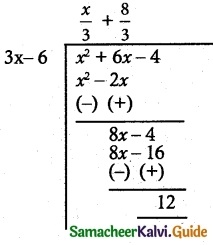
Question 2.
Sketch the graphs of the following functions
(i) y = –\(\frac { 1 }{ 3 }\) (x³ – 3x + 2)
(ii) y = x \(\sqrt { 4-x }\)
(iii) y = \(\frac { x^2+1 }{ x^2-4 }\)
(iv) y = \(\frac { 1 }{ 1+e^{-x} }\)
(v) y = \(\frac { x^3 }{ 24 }\) – log x
Solution:
(i) y = –\(\frac { 1 }{ 3 }\) (x³ – 3x + 2)
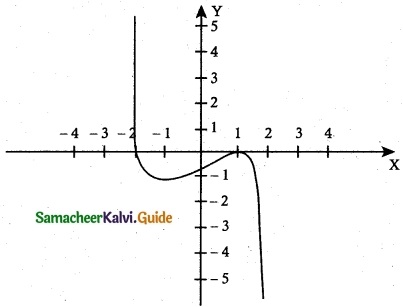
Factorizing we get
y = –\(\frac { 1 }{ 3 }\) (x – 1)² (x + 2) = f(x)
The domain and the range of the given function f(x) are the entire real line.
Putting y = 0, we get x = 1, 1, – 2. Hence the x-intercepts are (1, 0) and (- 2, 0) and by putting x = 0. We get y = –\(\frac { 2 }{ 3 }\). Therefore, the y-intercept is (0, –\(\frac { 2 }{ 3 }\))
f'(x) = \(\frac { (3x^2-3) }{ 3 }\) = -(x² – 1) = 1 – x²
f'(x) = 0 ⇒ 1 – x² = 0 ⇒ x = ±1
The critical points of the curve occur at x = ± 1 .
f”(x) = -2x
f”(1) = – 2 < 0, ∴ f(x) is maximum at x = 1 and the local maximum is f(1) = o
f”(-1) = 2 > 0, ∴ f(x) is minimum at x = -1 and the local minimum is
f(-1) = –\(\frac { 4 }{ 3 }\)
f”(x) = – 2x < 0 ∀ x > 0, ∴ The function is concave downward in the positive real line.
f”(x) = 2x > 0 ∀ x < 0, ∴ The function is concave upward in the negative real line.
Since f”(x) = 0 at x = 0 and f”(x) changes its sign when passing through x = 0.
Hence the point of inflection is (0, –\(\frac { 2 }{ 3 }\))
The curve has no asymptotes.
![]()
(ii) y = x\(\sqrt { 4-x }\)
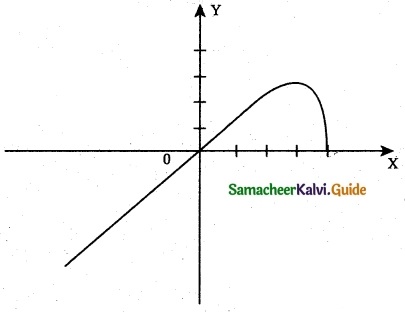
y = x\(\sqrt { 4-x }\) = f(x)
where x > 4 the curve does not exist and it exists for x ≤ 4
∴ The domain is (-∞, 4] and the Range is (-∞, \(\frac { 16 }{ 3√3 }\) ]
The curve passes through the origin. The curve intersects x-axis at (4, 0).
f'(x) = –\(\frac { x }{ 2 \sqrt{4-x} }\) + \(\sqrt { 4-x }\) = \(\frac { 8-3x }{ 2 \sqrt{4-x} }\)
f'(x) = 0 ⇒ 8 – 3x = 0 ⇒ x = \(\frac { 8 }{ 3 }\)
∴ Critical point of the curve occur at x = \(\frac { 8 }{ 3 }\)
f”(x) = \(\frac { 3x-16 }{ 4(4-x)^{\frac{3}{2}} }\)
f”(\(\frac { 8 }{ 3 }\)) = –\(\frac { 3√3 }{ 4 }\) < 0
∴ f(x) is maximum at x = \(\frac { 8 }{ 3 }\) and the local maximum f(\(\frac { 8 }{ 3 }\)) = \(\frac { 16 }{ 3√3 }\) and local minimum is 0 at x = 4 (from the graph)
f”(x) = \(\frac { 3x-16 }{ 4(4-x)^{\frac{3}{2}} }\) < 0 ∀ x < 4
∴ The curve is concave downward in the negative real line.
No point of inflection exists.
As x → ∞, y → ±∞ , and hence the curve does not have any asymptotes.
![]()
(iii) y = \(\frac { x^2+1 }{ x^2-4 }\)
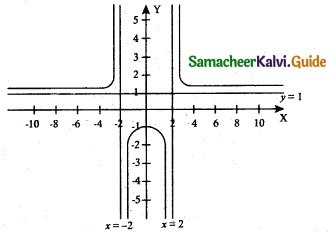
The domain of the given function f(x) is (-∞, -2) ∪ (-2, 2) ∪ (2, ∞)
ie. x < -2 (or) -2 < x < 2 (or) x > 2.
Range of f(x) is (-∞, –\(\frac { 1 }{ 4 }\)) ∪ (1, ∞)
i.,e. f(x) ≤ –\(\frac { 1 }{ 4 }\) (or) f(x) > 1.
Putting y = 0, x is unreal. Hence, there is no ‘x’ intercept.
By putting x = 0, we get y = –\(\frac { 1 }{ 4 }\).
∴ y intercept is (0, –\(\frac { 1 }{ 4 }\))
f'(x) = –\(\frac { 10x }{ (x^2-4)^2 }\)
f'(x) = 0 ⇒ x = 0,
∴ The critical point is at x = 0
f'(x) = \(\frac { 10(x^2-4)(3x^+4) }{ (x^2-4)^4 }\)
f'(0) = –\(\frac { 5 }{ 8 }\) < 0,
∴ f(x) is maximum at
x = 0. Hence the local maximum is f(0) = –\(\frac { 1 }{ 4 }\)
No points of inflection exist for the curve.
When x = ± 2, y = ∞
∴ Vertical asymptotes are x = 2 and x = -2 and Horizontal asymptote is y = 1.
![]()
(iv) y = \(\frac { 1 }{ 1+e^{-x} }\)
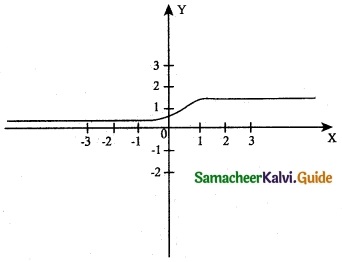
The Domain of the function f(x) is the entire real line.
ie., (-∞, ∞) ⇒ -∞ < x < ∞ and the range is (0, 1) ie., 0 < f(x) < 1
No ‘x’ intercept for f(x) and when x = 0
y = \(\frac { 1 }{ 2 }\)
∴ The ‘y’ intercept is (0, \(\frac { 1 }{ 2 }\))
f'(x) = \(\frac { e^{-x} }{ (1+e^{-x})^2 }\)
f'(x) = 0 ⇒ which is absurd. Hence there is no extremum.
No vertical asymptote for the curve exist and the Horizontal asymptotes are y = 1 and y = 0.
![]()
(v) y = \(\frac { x^3 }{ 24 }\) – log x
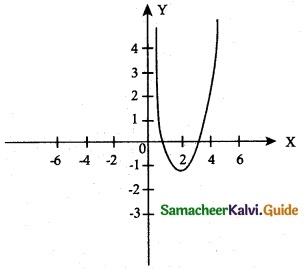
The curve exists only for positive values of ‘x’ (x > 0) ie., domain is (0, ∞) and
The range is (\(\frac { 1 }{ 3 }\) – log e², ∞)
No intersection points are possible
f'(x) = \(\frac { x^2 }{ 8 }\) – \(\frac { 1 }{ x }\)
f'(x) = 0 ⇒ x³ – 8 = 0 ⇒ x = 2
∴ Critical point occur at x = 2
f'(x) = \(\frac { x }{ 4 }\) + \(\frac { 1 }{ x^2 }\)
f”(2) = \(\frac { 3 }{ 4 }\) > 0,
∴ f(x) is mimmum at x = 2 and the local minimum is f(2) = \(\frac { 1 }{ 3 }\) – log e²
No point of inflection exists.
No Horizontal asymptotes are possible, but the vertical asymptote is x = 0 (y-axis).
![]()