Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 Applications of Differential Calculus Ex 7.7 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.7
Question 1.
Find intervals of concavity and points of inflection for the following functions:
(i) f(x) = x(x – 4)³
(ii) f(x) = sin x + cos x, 0 < x < 2π
(iii) f(x) = \(\frac { 1 }{ 2 }\)(ex – e-x)
Solution:
(i) f(x) = x(x – 4)³
f'(x) = 3x(x – 4)² + (x – 4)³(1)
= (x – 4)² (4x – 4) = 4 (x – 4)² (x – 1)
f'(x) = 4 [(x-4)² (1) + (x – 1) 2 (x – 4)]
= 4(x – 4)(x – 4 + 2x – 2)
= 4(x – 4)(3x – 6) = 12(x – 4)(x – 2)
f'(x) = 0 ⇒ 12 (x – 4) (x – 2) = 0
Critical points x = 2, 4

The intervals are (- ∞, 2), (2, 4) and (4, ∞)
In the interval (-∞, 2), f”(x) > 0 ⇒ Curve is Concave upward
In the interval (2, 4), f”(x) < 0 ⇒ Curve is Concave downward.
In the interval (4, ∞), f”(x) > 0 ⇒ Curve is Concave upward.
The curve is concave upward in
(-∞, 2), (4, ∞) it is concave downward in (2, 4).
f”(x) changes its sign when passing through x = 2 and x = 4
Now f(2) = 2 (2 – 4)³ = -16 and f(4) = 4 (4 – 4)³ = 0
∴ The points of inflection are (2, -16) and (4, 0).
![]()
(ii) f(x) = sin x + cos x, 0 < x < 2π
f'(x) = cos x – sin x
f”(x) = – sin x – cos x
f'(x) = 0 ⇒ sin x + cos x = 0
Critical points x = \(\frac { 3π }{ 4 }\), \(\frac { 7π }{ 4 }\)

The intervals are (0, \(\frac { 3π }{ 4 }\)), (\(\frac { 3π }{ 4 }\), \(\frac { 7π }{ 4 }\)) and (\(\frac { 7π }{ 4 }\), 2π)
In the interval (0, \(\frac { 3π }{ 4 }\)), f'(x) < 0 ⇒ curve is concave down.
In the interval (\(\frac { 3π }{ 4 }\), \(\frac { 7π }{ 4 }\)), f'(x) > 0 ⇒ curve is concave up.
In the interval (\(\frac { 7π }{ 4 }\), 2π), f'(x) < 0 ⇒ curve is concave down.
The curve is concave upward in (\(\frac { 3π }{ 4 }\), \(\frac { 7π }{ 4 }\)) and concave downward in (0, \(\frac { 3π }{ 4 }\)) and (\(\frac { 7π }{ 4 }\), 2π)
f'(x) changes its sign when passing through x = \(\frac { 3π }{ 4 }\) and x = \(\frac { 7π }{ 4 }\)

![]()
(iii) f(x) = \(\frac { 1 }{ 2 }\) (ex – e-x)
f'(x) = \(\frac { 1 }{ 2 }\) (ex + e-x)
f”(x) = \(\frac { 1 }{ 2 }\) (ex – e-x)
f”(x) = 0 ⇒ \(\frac { 1 }{ 2 }\) (ex – e-x) = 0
Critical point x = 0
The intervals are (-∞, o) and (0, ∞)
In the interval (-∞, 0), f”(x) < 0 ⇒ curve is concave down.
In the interval (0, ∞), f(x) > 0 ⇒ curve is concave up.
∴ The curve is concave up in (0, ∞) and concave down in (-∞, 0).
f'(x) changes its sign when passing through x = 0
Now f(0) = – (e° – e°) = \(\frac { 1 }{ 2 }\) (1 – 1) = 0
∴ The point of inflection is (0, 0).
Question 2.
Find the local extrema for the following functions using second derivative test:
(i) f(x) = -3x5 + 5x3
(ii) f(x) = x log x
(iii) f(x) = x² e-2x
Solution:
(i) f(x) = – 3x5 + 5x3
f'(x) = 0, f”(x) = -ve at x = a
⇒ x = a is a maximum point
f'(x) = 0, f”(x) = +ve at x = 6
⇒ x = b is a minimum point
f(x) = – 3x5 + 5x3
f’ (x) = -15x4 + 15x2
f”(x) = -60x3 + 30x
f'(x) = 0 ⇒ – 15x2 (x2 – 1) = 0
⇒ x = 0, +1, -1
at x = 0, f”(x) = 0
at x = 1, f”(x) = -60 + 30 = – ve
at x = -1, f”(x) = 60 – 30 = + ve
So at x = 1, f'(x) = 0 and f”(x) = -ve
⇒ x = 1 is a local maximum point.
and f(1) = 2
So the local maximum is (1, 2)
at x = -1, f'(x) = 0 and f”(x) = +ve
⇒ x = -1 is a local maximum point and f(-1) = -2.
So the local minimum point is (-1, -2)
∴ a local minimum is -2 and the local maximum is 2.
![]()
(ii) f(x) = x log x
f'(x) = x – \(\frac { 1 }{ 4 }\) + log x = 1 + log x
For maximum or minimum
f'(x) = 0 ⇒ 1 + log x = 0
⇒ log x = -1
x = e-1 = \(\frac { 1 }{ e }\)
f”(x) = \(\frac { 1 }{ x }\)
at x = \(\frac { 1 }{ e }\), f”(x) > 0 ⇒ f(x) attains minimum.
∴ Local minimum f(\(\frac { 1 }{ e }\)) = \(\frac { 1 }{ e }\) log (\(\frac { 1 }{ e }\))
= \(\frac { 1 }{ e }\)(-1) = –\(\frac { 1 }{ e }\)
(iii) f(x) = x2 e-2x
f'(x) = x2[-2e-2x] + e-2x (2x)
= 2e-2x (x – x2)
f”(x) = 2e-2x(1 – 2x) + (x – 2) (-4e-2x)
= 2e-2x [(1 – 2x) + (x – x2) (- 2)]
= 2e-2x [2x2 – 4x + 1]
f'(x) = 0 ⇒ 2e-2x(x – x2) = 0
⇒ x (1 – x) = 0
⇒ x = 0 or x = 1
at x = 0, f”(x) = 2 × 1 [0 – 0 + 1] = +ve
⇒ x = 0 is a local minimum point and the minimum value is f(0) = 0 at x = 1,
f”(x) = 2e-2 [2 – 4 + 1] = -ve
⇒ x = 1 is a local maximum point and the maximum value is f(1) = \(\frac{1}{e^{2}}\)
Local maxima \(\frac{1}{e^{2}}\) and local minima = 0
![]()
Question 3.
For the function f(x) = 4x³ + 3x² – 6x + 1 find the intervals of monotonicity, local extrema, intervals of concavity and points of inflection.
Solution:
(x) = 4x³ + 3x² – 6x + 1
Monotonicity
f(x) = 4x³ + 3x² – 6x + 1
f'(x) = 12x² + 6x – 6
f'(x) = 0 ⇒ 6(2x² + x – 1) = 0
x = -1, \(\frac { 1 }{ 2 }\) (Stationary points)
∴ The intervals of monotonicity are (-∞, -1), (-1, \(\frac { 1 }{ 2 }\)) and (\(\frac { 1 }{ 2 }\), ∞)
In (-∞, -1), f'(x) > 0 ⇒ f(x) is strictly increasing
In (-1, \(\frac { 1 }{ 2 }\)), f'(x) < 0 ⇒ f(x) is strictly decreasing
In (\(\frac { 1 }{ 2 }\), ∞) f'(x) > 0 ⇒ f(x) is strictly increasing
f(x) attains local maximum as f'(x) changes its sign from positive to negative when passing through x = -1
∴ Local maximum f(-1) = -4 + 3 + 6 + 1 = 6
f(x) attains local minimum as f'(x) changes its sign from negative to positive when passing through x = \(\frac { 1 }{ 2 }\)
∴ Local minimum f(\(\frac { 1 }{ 2 }\))
= 4(\(\frac { 1 }{ 8 }\)) + 3(\(\frac { 1 }{ 4 }\)) – 6(\(\frac { 1 }{ 2 }\)) + 1
= \(\frac { 1 }{ 2 }\) + \(\frac { 3 }{ 4 }\) – + 1 = –\(\frac { 3 }{ 4 }\)
f(x) = 4x³ + 3x² – 6x + 1
f'(x) = 12x² + 6x – 6
f”(x) = 24x + 6
f’(x) = 0 ⇒ 24x + 6 = 0
x = –\(\frac { 6 }{ 24 }\) = –\(\frac { 1 }{ 4 }\) (critical points)
∴ The intervals are (∞, \(\frac { 1 }{ 4 }\)) and (\(\frac { 1 }{ 4 }\), ∞) f”(x) > 0
In the interval (-∞, –\(\frac { 1 }{ 4 }\)), f”(x) < 0 ⇒ curve is concave down.
In the interval (-\(\frac { 1 }{ 4 }\), ∞), f”(x) > 0 ⇒ curve is concave up.
The curve is concave upward in (-\(\frac { 1 }{ 4 }\), ∞) and concave downward in (-∞, –\(\frac { 1 }{ 4 }\))
f”(x) changes its sign when passing through x = –\(\frac { 1 }{ 4 }\)
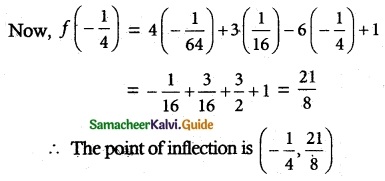
![]()