Samacheer Kalvi 12th Maths Guide Chapter 6 Applications of Vector Algebra Ex 6.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 Applications of Vector Algebra Ex 6.4 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.4

Question 1.
Find the non-parametric form of vector equation and Cartesian equations of the straight line passing through the point with position vector 4\(\hat { i }\) + 3\(\hat { j }\) – 7\(\hat { k }\) and parallel to the vector 2\(\hat { i }\) – 6\(\hat { j }\) + 7\(\hat { k }\)
Solution:

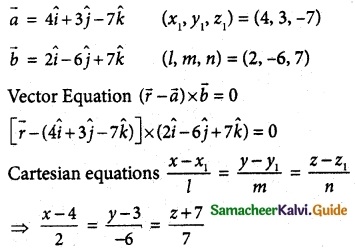
Question 2.
Find the parametric form of vector equation and Cartesian equations of the straight line passing through the point (-2, 3, 4) and parallel to the straight line \(\frac { x-1 }{ -4 }\) = \(\frac { y+3 }{ 5 }\) = \(\frac { 8-z }{ 6 }\)
Solution:
\(\overline { a }\) = -2\(\hat { i }\) + 3\(\hat { j }\) + 4\(\hat { k }\) (x₁, y₁, z₁) = (-2, 3, 4)
\(\overline { b }\) = -4\(\hat { i }\) + 5\(\hat { j }\) + 6\(\hat { k }\) (l, m, n) = (-4, 5, 6)
vector equation

Question 3.
Find the points where the straight line passes through (6, 7, 4) and (8, 4, 9) cuts the xz and yz planes.
Solution:
The straight line passes through the points (6, 7, 4) and (8, 4, 9)
∴ Direction ratios are 2, -3, 5
So the straight line is parallel to 2\(\hat { i }\) – 3\(\hat { j }\) + 5\(\hat { k }\)
∴ Vector equation is

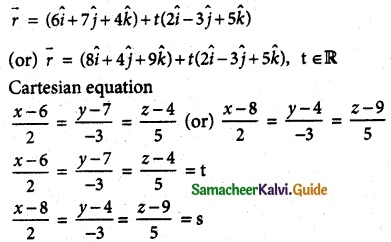
An arbitrary point on the straight line is of the form (2t + 6, -3t + 7, 5t + 4) or (2s + 8, -3s + 4, 5s + 9)
(i) xz plane mean y = 0
-3t + 7 = 0
3t = 7
t = \(\frac { 7 }{ 3 }\)
Point = (2(\(\frac { 7 }{ 3 }\)) + 6, 0, 5(\(\frac { 7 }{ 3 }\)) + 4) = (\(\frac { 32 }{ 3 }\), 0, \(\frac { 47 }{ 3 }\))

(ii) The straight Line cuts yz-plane
So we get x = 0
2t + 6 = 0 ⇒ 2t = -6
t = -3
-3t + 7 = -3 (-3) + 7 = 9 + 7 = 16
5t + 4 = 5(-3) + 4 = -15 + 4 = -11
The required point (0, 16, -11).

Question 4.
Find the direction cosines of the straight line passing through the points (5, 6, 7) and (7, 9, 13). Also, find the parametric form of vector equation and Cartesian equations of the straight line passing through two given points.
Solution:
Given points (5, 6, 7) and (7, 9, 13)
Direction ratios are (2, 3, 6)
So the straight line is parallel to 2\(\hat { i }\) + 3\(\hat { j }\) + 6\(\hat { k }\)

Question 5.
Find the acute angle between the following lines. ]
(i) \(\overline { r }\) = (4\(\hat { i }\) – \(\hat { j }\)) + t(\(\hat { i }\) + 2\(\hat { j }\) – 2\(\hat { k }\)),
\(\overline { r }\) = (\(\hat { i }\) – 2\(\hat { j }\) + 4\(\hat { k }\)) + s(-\(\hat { i }\) – 2\(\hat { j }\) + 2\(\hat { k }\))
(ii) \(\frac { x+4 }{ 3 }\) = \(\frac { y-7 }{ 4 }\) = \(\frac { z+5 }{ 5 }\), \(\overline { r }\) = 4\(\hat { k }\) + t(2\(\hat { i }\) + \(\hat { j }\) + \(\hat { k }\))
(iii) 2x = 3y = -z and 6x = -y = -4z.
Solution:

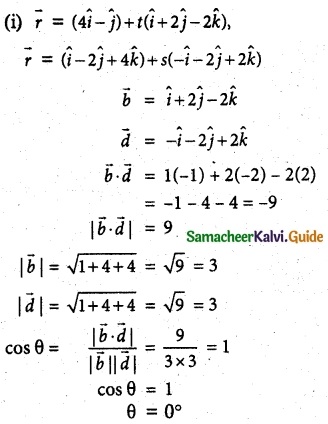
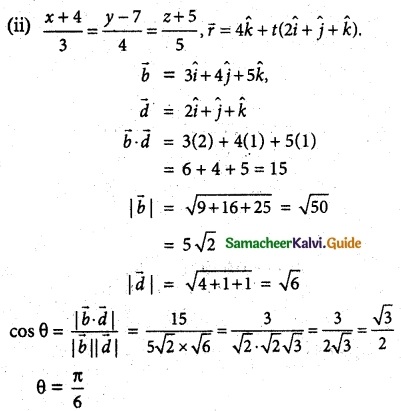
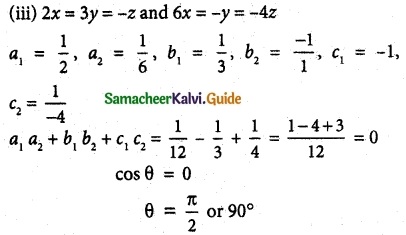
Question 6.
The vertices of ΔABC are A(7, 2, 1), 5(6, 0, 3), and C(4, 2, 4). Find ∠ABC.
Solution:

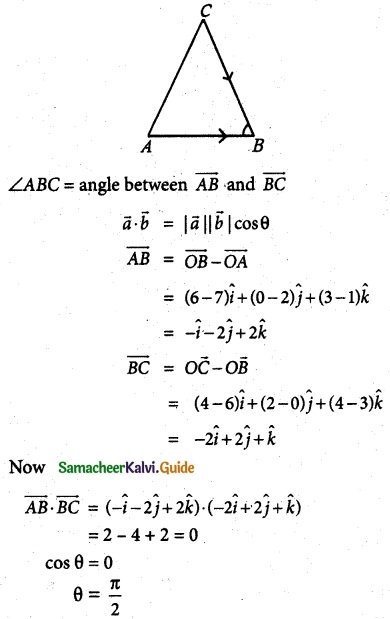
Question 7.
If the straight line joining the points (2, 1, 4) and (a – 1, 4, -1) is parallel to the line joining the points (0, 2, b – 1) and (5, 3, -2) find the values of a and b.
Solution:
(i) Points are (2, 1, 4) (a – 1, 4, -1)
Cartesian equation

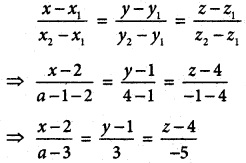
(ii) Points are (0, 2, b – 1) (5, 3, -2)
Cartesian equation

Question 8.
If the straight lines \(\frac { x-5 }{ 5m+2 }\) = \(\frac { 2-y }{ 5 }\) = \(\frac { 1-z }{ -1 }\) and x = \(\frac { 2y+1 }{ 4ni }\) = \(\frac { 1-z }{ -3 }\) are perpendicular to each other, find the value of m.
Solution:
If the lines are perpendicular
b₁d₁ + b₂d₂ + b₃d₃ = 0
(5m + 2) – 5(2m) + 1(+3) = 0
5m + 2 – 10m + 3 = 0
-5m = -5
m = \(\frac { -5 }{ -5 }\) = 1
⇒ ∴ m = 1

Question 9.
Show that the points (2, 3, 4), (-1, 4, 5) and (8, 1, 2) are collinear.
Solution:

∴ given points are collinear.