Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 4 Inverse Trigonometric Functions Ex 4.3 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.3
Question 1.
Find the domain of the following functions
(i) tan-1 (\(\sqrt {9-x^2}\))
(ii) \(\frac {1}{2}\) tan-1 (1 – x²) – \(\frac {π}{4}\)
Solution:
(i) f(x) = \(\tan ^{-1}(\sqrt{9-x^{2}})\)
We know the domain of tan-1 x is (-∞, ∞) and range is \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
So, the domain of f(x) = \(\tan ^{-1}(\sqrt{9-x^{2}})\) is the set of values of x satisfying the inequality
\(-\infty \leq \sqrt{9-x^{2}} \leq \infty\)
⇒ 9 – x2 ≥ 0
⇒ x2 ≤ 9
⇒ |x| ≤ 3
(ii) Range of tan-1 x is R
-∞ < 1 – x² < ∞
-∞ < -x² < ∞
-∞ < x < ∞
x ∈ R
Domain = R
![]()
Question 2.
Find the value of
(i) tan-1(tan\(\frac {5π}{4}\))
(ii) tan-1(tan(-\(\frac {π}{6}\)))
Solution:
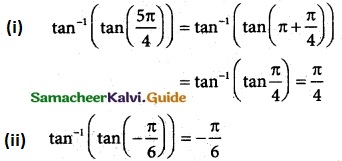
![]()
Question 3.
Find the value of
(i) tan(tan-1(\(\frac {7π}{4}\)))
(ii) tan(tan-1(1947))
(iii) tan(tan-1(-0.2021))
solution:
We know that tan(tan-1 x) = x
(i) \(\tan \left(\tan ^{-1} \frac{7 \pi}{4}\right)=\frac{7 \pi}{4}\)
(ii) tan(tan-1(1947))= 1947
(iii) tan(tan-1 (-0.2021)) = -0.2021
![]()
Question 4.
Find the value of
(i) tan(cos-1(\(\frac {1}{2}\)) – sin-1(-\(\frac {1}{2}\)))
(ii) sin(tan-1(\(\frac {1}{2}\)) – cos-1(\(\frac {4}{5}\)))
(iii) cos(sin-1(\(\frac {4}{5}\)) – tan-1(\(\frac {3}{4}\)))
solution:
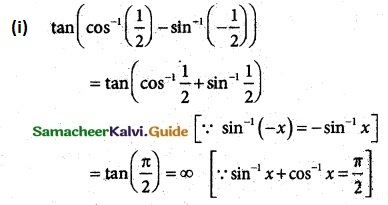
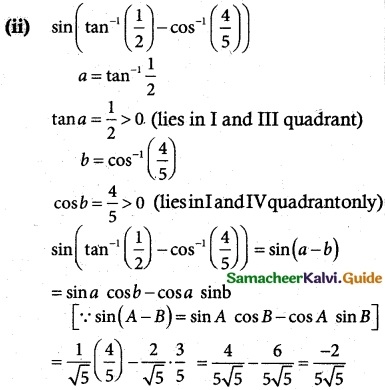
![]()

![]()