Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 Theory of Equations Ex 3.5 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.5
Question 1.
Solve the following equations
(i) sin² x – 5 sin x + 4 = 0
Solution:
sin2x – 5sinx + 4 = 0
Let y = sin x
(y2 – 5y + 4 = 0
(y – 1) (y – 4) = 0
(y – 1) = o or (y – 4) = 0
y = 1 or y = 4
sin x = 1 or sin x = 4 [not possible since sin x ≤ 1]
sin x = sin \(\frac{\pi}{2}\)
x = nπ + (-1)n α, n ∈ z.
x = nπ + (-1)n \(\frac{\pi}{2}\)
(ii) 12x³ + 8x = 29x² – 4 = 0
Solution:
12x³ – 29x² + 8x + 4 = 0
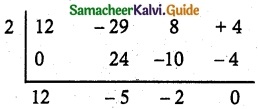
12x² – 5x – 2 = 0
12x² – 8x + 3x – 2 = 0
4x(3x – 2) + 1(3x – 2) = 0
(3x – 2)(4x + 1) = 0
3x = 2, 4x = -1
x = \(\frac{2}{3}\) or x = –\(\frac{1}{4}\)
The roots are 2, \(\frac{2}{3}\), –\(\frac{1}{4}\).
![]()
Question 2.
Examine for the rational roots of
(i) 2x³ – x² – 1 = 0
Solution:
Sum of co-efficients = 2 – 1 – 1 = 0
⇒ x = 1 is a factor.

Which is imaginary root
∴ x = 1 is rational root.
(ii) x8 – 3x + 1 = 0
Solution:
an = 1; a0 = 1
If \(\frac{p}{q}\) is a root of the polynomial. (p, q) = 1
By rational root theorem, it has no rational roots.
![]()
Question 3.
Solve: 8x\(\frac{3}{2n}\) – 8x\(\frac{-3}{2n}\) = 63.
Solution:
Put k = \(\frac{3}{2n}\) ∴ 8xk – 8x-k = 63
8xk – \(\frac{8}{x^k}\) = 63
8x2k – 8 = 63xk
8x2k – 63xk – 8 = 0
(xk – 8) (8xk + 1) = 0
xk – 8 = 0
xk = 8
x\(\frac{3}{2n}\) = 8
x = 8\(\frac{3}{2n}\) (2³)\(\frac{3}{2n}\) = (2²)n = 4n
∴ x = 4n is a root of the equation.
Question 4.
Solve: 2\(\sqrt{\frac{x}{a}}\) + 3\(\sqrt{\frac{a}{x}}\) = \(\frac{b}{a}\) = \(\frac{6a}{b}\)
Solution:
put \(\sqrt{\frac{x}{a}}\) = y

![]()
Question 5.
Solve the equations
(i) 6x4 – 35x³ + 62x² – 35x + 6 = 0
Solution:
This is Type I even degree reciprocal equation. Hence it can be rewritten as
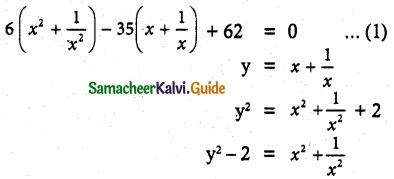
(1) ⇒ 6(y² – 2) – 35y + 62 = 0
6y² – 12 – 35y + 62 = 0
6y² – 35y + 50 = 0
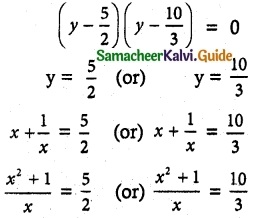
2x² + 2 – 5x = 0 (or) 3x² + 3 = 10x
2x² – 5x + 2 = 0 (or) 3x² – 10x + 3 = 0
x = 2, \(\frac{1}{2}\) (or) x = 3, \(\frac{1}{3}\)
Roots are 2, \(\frac{1}{2}\), 3 and \(\frac{1}{3}\)
![]()
(ii) x4 + 3x³ – 3x – 1 = 0
Solution:
(x – 1) and (x + 1) is a factor.
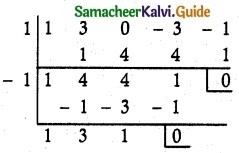
(x – 1)(x + 1)(x² + 3x + 1) = 0
x – 1 = 0 (or) x + 1 = 0 (or) x² + 3x + 1 = 0
x = 1 (or) x = -1 (or) x² + 3x = -1

Question 6.
Find all real numbers satisfying
Solution:
4x – 3 (2x+2) + 25 = 0
⇒ (22)x – 3(2x . 22) + 25 = 0
(22)x – 12 . 2x+ 32 = 0
Let y = 2x
y2 – 12y + 32 = 0
⇒ (y – 4) (y – 8) = 0
y – 4 = 0 or y – 8 = 0
Case (i): 2x = 4
⇒ 2x = (2)2
⇒ x = 2
Case (ii): 2x = 8
⇒ 2x = (2)3
⇒ x = 3
∴ The roots are 2, 3
![]()
Question 7.
Solve the equation 6x4 – 5x³ – 38x² – 5x + 6 = 0 if it is known that \(\frac{1}{3}\) is a solution.
Solution:
6x4 – 5x³ – 38x² – 5x + 6 = 0
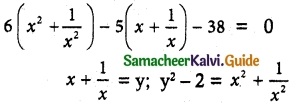
6(y² – 2) – 5y – 38 = 0
6y² – 12 – 5y – 38 = 0
6y² – 5y – 50 = 0
6y² – 20y + 15y – 50 = 0
2y(3y – 10) + 5(3y – 10) = 0
(3y – 10)(2y + 5) = 0
3y = 10, 2y = -5

3x² + 3 = 10x, 2x² + 2 = -5x
3x² – 10x + 3 = 0, 2x² + 5x + 2 = 0
(x – 3)(3x – 1) = 0, (2x + 1)(x + 1) = 0
x = 3, x = \(\frac{1}{3}\) or x = \(\frac{-1}{2}\), x= -2
The roots are 3, \(\frac{1}{3}\), -2, \(\frac{-1}{2}\).
![]()