Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 10 Ordinary Differential Equations Ex 10.3 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.3
Question 1.
Find the differential equation of the family of (i) all non-vertical lines in a plane
(ii) all non horizontal lines in a plane.
Solution:
(i) The equation of the family of non vertical lines in a plane ax + by = 1, b ≠ 0, a ∈ R
Given equation is ax + by = 1 …….. (1)
Differentiating equation (1) with respect to ‘x’ we get
a + b \(\frac { dy }{ dx }\) = 0
∵ 2 arbitrary constant,
∴ Differentiating twice continuously
Again differentiating above equation with respect to ‘x’, we get
0 + b \(\frac { d^2y }{ dx^2 }\) = 0
\(\frac { d^2y }{ dx^2 }\) = 0 [∵ b ≠ 0]
\(\frac { d^2y }{ dx^2 }\) = 0 is a required differential equation.
(ii) The equation of the family of non horizontal
lines in a,plane ax + by = 1, a ≠ 0 & b ∈ R
Given equation is ax + by = 1 ……… (1)
Differentiating equation (1) with respect to ‘y’, we get
a \(\frac { dx }{ dy }\) + b = 0
∵ 2 arbitrary constant,
∴ Differentiating twice continuously
Again differentiating we get
a \(\frac { d^2x }{ dy^2 }\) = 0 [∵ a ≠ 0]
\(\frac { d^2x }{ dy^2 }\) = 0 is a required differential equation.
![]()
Question 2.
Form the differential equation of all straight lines touching the circle x² + y² = r²
Solution:
Given circle equation be x² + y² = r²
Let y = mx + c be all straight lines which towards the given circle x² + y² = r²
The condition for y = mx + c ……. (1)
be a tangent to the circle x² + y² = r²
be c² = r² (1 + m²) ⇒ c = r \(\sqrt { 1+m^2 }\)
Substituting c value in equation (1), we get
y = mx + r \(\sqrt { 1+m^2 }\)
y – mx = r\(\sqrt { 1+m^2 }\) ……. (2)
Differentiating equation (2) w.r.t x, we get
\(\frac { dy }{ dx }\) – m = 0
\(\frac { dy }{ dx }\) = m …….. (3)
substituting equation (3) in equation (2), we get;

Which is a required differential equation.
![]()
Question 3.
Find the differential equation of the family of circles passing through the origin and having their centres on the x-axis.
Solution:
Given the circles centre on x-axis & the circle is passing through the origin.
Let it be (r, 0) & its radius r.
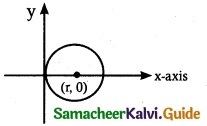
Equation of the circle is
(x – a)² + (y – b)² = r²
(x – r)² + (y – 0)² = r²
x² – 2xr + r² + y² = r²
x² – 2xr + y² = r² – r²
x² – 2xr + y² = 0 ……. (1)
Differentiating equation (1) with respect to ‘x’, we get
2x – 2r + 2y \(\frac { dy }{ dx }\) = 0 dx
2x + 2y\(\frac { dy }{ dx }\) = 2r
x + y\(\frac { dy }{ dx }\) = r
Substituting r value in equation (1), we get
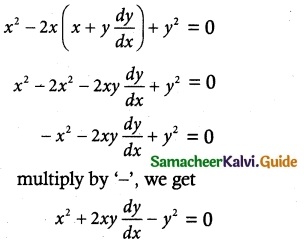
Which is a required differential equation.
![]()
Question 4.
Find the differential equation of the family of all the parabolas with latus rectum 4a and whose axes are parallel to the x-axis.
Solution:
Given the equation of family of parabolas with latus rectum 4a and axes are parallel to x-axis then
(y – b)² = 4a (x – a), where (a, b) is the vertex of parabola.
y² – 2yb + b² = 4ax – 4a² ……. (1)
Differentiating equation (1) with respect to x, we get

Differentiating equation (2) with respect to ‘x’, we get
yy”+ y’y’ = by”
yy” + y’2 = by” ……. (3)
Substituting the b value in (3), we get
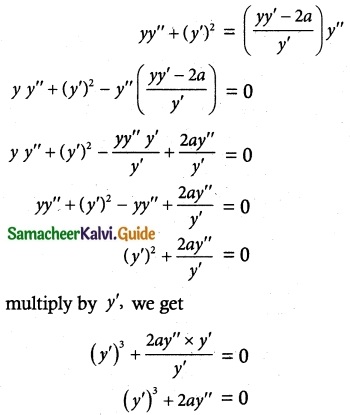
Which is a required differential equation.
![]()
Question 5.
Find the differential equation of the family of parabolas with vertex at (0, -1) and having axis along the y axis.
Solution:
Equation of the family of parabolas with vertex at (0, -1) and having axis along the y-axis is
(x – 0)² = 4a(y + 1)
x² = 4a (y + 1) ……. (1)
x² = 4 ay + 4a
Differentiating equation (1) with respect to ‘x’, we get
2x = 4a y’
\(\frac { 2x }{ y’ }\) = 4a
Substituting 4a value in equation (1), we get
x² = \(\frac { 2x }{ y’ }\)(y + 1)
\(\frac { x^2 }{ x }\) = \(\frac { 2 }{ y’ }\)(y + 1)
x = \(\frac { 2 }{ y’ }\) (y + 1)
xy’ = 2 (y + 1)
xy’ = 2y + 2
xy’ – 2y – 2 = 0 is a required differential equation.
![]()
Question 6.
Find the differential equations of the family of all the ellipses having foci on the y-axis and centre at the origin.
Solution:
The equation of the family of ellipses having centre at the origin & foci on the y-axis, is given by \(\frac { x^2 }{ a^2 }\) + \(\frac { y^2 }{ b^2 }\) = 1 ……… (1)
where b > a & a, b are the parameters or a,b are arbitrary constant.
Differentiating equation (1) twice successively, (because we have two arbitrary constant) we get

Equ (3) – (2) we get

is the required differential equation.
![]()
Question 7.
Find the differential equation corresponding to the family of curves represented by the equation y = Ae8x + Be -8x, where A and B are arbitrary constants.
Solution:
Given y = Ae8x + Be-8x …….. (1)
where A & B are aribitrary constants differentiating equation (1) twice successively (because we have two arbitrary constant), we get
\(\frac { dy }{ dx }\) = Ae8x + Be-8x (-8)
\(\frac { dy }{ dx }\) = 8Ae8x – 8Be-8x ……… (2)
\(\frac { d^2y }{ dx^2 }\) = 8Ae8x (8) – Be-8x (-8)
= 64Ae8x + 64Be-8x
= 64[Ae8x + Be-8x] ……….. (3)
Substituting eqn (1) in eqn (3), we get
\(\frac { d^2y }{ dx^2 }\) = 64 y
\(\frac { d^2y }{ dx^2 }\) – 64 y = 0 is the required differential equation.
![]()
Question 8.
Find the differential equation of the curve represented by xy = aex + be-x + x²
Solution:
Given xy = aex + be-x + x² ……… (1)
where a & b are aribitrary constant,
differentiate equation (1) twice successively,
because we have two arbitray constant.
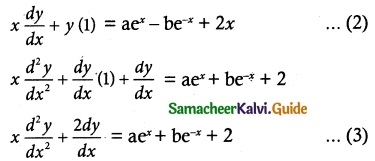
From (1), we get xy – x² = aex + be-x …….. (4)
Substituting equation (4) in (3), we get
∴ x \(\frac { d^2y }{ dx^2 }\) + \(\frac { 2dy }{ dx }\) – xy + x² – 2 = 0 is the required differential equation.
![]()