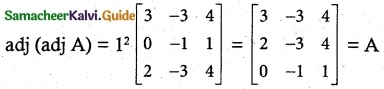Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.8 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.8
Choose the Most Suitable Answer.
Question 1.
If |adj(adj A) |=| A|9, then the order of the square matrix A is:
(a) 3
(b) 4
(c) 2
(d) 5
Solution:
(b) 4
Hint:
Since |adj(adj A)| = |A|(n – 1)2
(n – 1)2 = 9 = 3²
n – 1 = 3
n = 4
![]()
Question 2.
If A is a 3 × 3 non-singular matrix such that AAT = AT A and B = A-1AT, then BBT =
(a) A
(b) B
(C) I3
(d) BT
Solution:
(C) I
Hint:
AAT = ATA and B = A-1AT
BT = (A-1)T(AT)T = (A-1)T A
BB-1 = (A-1 AT) (A-1)T A = A-1 (AA-1)T A
= A-1 (I)T A = A-1 A = I3
Question 3.
If A = \(\begin{bmatrix} 3 & 5 \\ 1 & 2 \end{bmatrix}\) B = adj A and C = 3A, then \(\frac{|adj B|}{|C|}\) =
(a) \(\frac{1}{3}\)
(b) \(\frac{1}{9}\)
(C) \(\frac{1}{4}\)
(d) 1
Solution:
(a) \(\frac{1}{3}\)
Hint:

![]()
Question 4.
If A \(\begin{bmatrix} 1 & -2 \\ 1 & 4 \end{bmatrix}\) = \(\begin{bmatrix} 6 & 0 \\ 0 & 6 \end{bmatrix}\), then A:
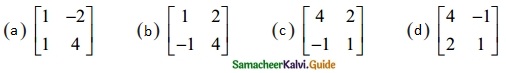
Solution:
(c) \(\begin{bmatrix} 4 & 2 \\ -1 & 1 \end{bmatrix}\)
Hint:

Solve the equations we get
a = 4, b = 2, c = -1, d = 1
A = \(\begin{bmatrix} 4 & 2 \\ -1 & 1 \end{bmatrix}\)
Question 5.
If A = \(\begin{bmatrix} 7 & 3 \\ 4 & 2 \end{bmatrix}\) then 9I2 – A =
(a) A-1
(b) \(\frac{A^{-1}}{2}\)
(c) 3A-1
(d) 2A-1
Solution:
(d) 2A-1
Hint:
|A| = 14 – 12 = 2
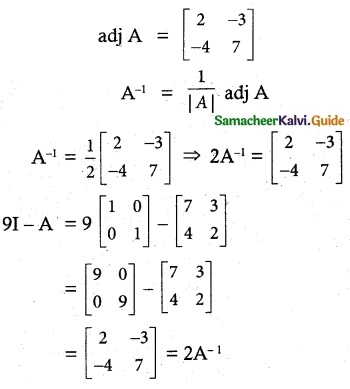
![]()
Question 6.
If A = \(\begin{bmatrix} 2 & 0 \\ 1 & 5 \end{bmatrix}\) and B = \(\begin{bmatrix} 1 & 4 \\ 2 & 0 \end{bmatrix}\) then |adj (AB)| =
(a) -40
(b) -80
(c) -60
(d) -20
Solution:
(b) -80
Hint:

∴ |adj (AB)| = 8 – 88 = -80
Question 7.
If P = \(\left[ \begin{matrix} 1 & x & 0 \\ 1 & 3 & 0 \\ 2 & 4 & -2 \end{matrix} \right] \) is the adjoint of 3 × 3 matrix A and |A| = 4, then x is
(a) 15
(b) 12
(c) 14
(d) 11
Solution:
(d) 11
Hint:
Since |adj A| = |A|n – 1 (n = 3)
1(-6 + 0) – x(-2) = 4²
-6 + 2x = 16
2x = 16 + 6 = 22
x = 11
![]()
Question 8.
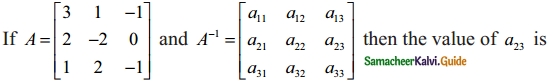
(a) 0
(b) -2
(c) -3
(d) -1
Solution:
(d) -1
Hint:
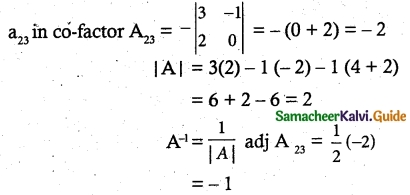
Question 9.
If A, B and C are invertible matrices of some order, then which one of the following is not true?
(a) adj A = |A|A-1
(b) adj (AB) = (adj A)(adj B)
(c) det A-1 = (det A)-1
(d) (ABC)-1 = C-1B-1A-1
Solution:
(b) adj (AB) = (adj A)(adj B)
Hint:
adj (AB) ≠ (adj A)(adj B)
![]()
Question 10.
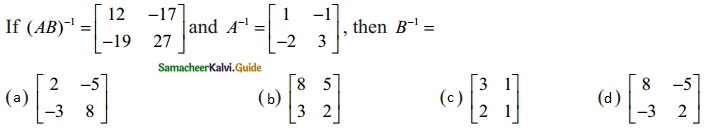
Solution:
(a) \(\begin{bmatrix} 2 & -5 \\ -3 & 8 \end{bmatrix}\)
Hint:
(AB)-1 = B-1 A-1
(AB)-1 A = B-1 [A-1]A
(AB)-1 A = B-1
(A-1)-1 = A
|A-1| = 3 – 2 = 1

Question 11.
If ATA-1 is symmetric, then A² =
(a) A-1
(b) (AT)²
(c) AT
(d) (A-1)²
Solution:
(b) (AT)²
Hint:
(AT A-1)T = AT A-1
(A-1)T (AT)T = AT A-1
(A-1)T A = AT A-1
AT (A-1)T AA = (AT) AT A-1 A
(pre and post multiply by AT and A)
A2 = (AT)²
![]()
Question 12.
If A is a non-singular matrix such that A-1 = \(\begin{bmatrix} 5 & 3 \\ -2 & -1 \end{bmatrix}\), then (AT)-1 =
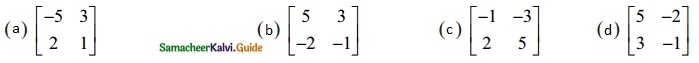
Solution:
(d) \(\begin{bmatrix} 5 & -2 \\ 3 & -1 \end{bmatrix}\)
Hint:
A-1 = \(\begin{bmatrix} 5 & 3 \\ -2 & -1 \end{bmatrix}\)
Since (AT)-1 = (A-1)T = \(\begin{bmatrix} 5 & -2 \\ 3 & -1 \end{bmatrix}\)
Question 13.
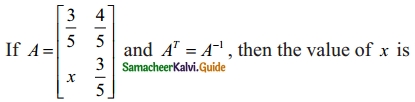
(a) \(\frac{-4}{5}\)
(b) \(\frac{-3}{5}\)
(c) \(\frac{3}{5}\)
(d) \(\frac{4}{5}\)
Solution:
(a) \(\frac{-4}{5}\)
Hint:
Since AT = A-1
AAT = I
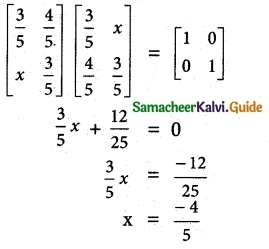
![]()
Question 14.
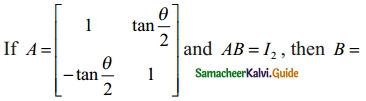
(a) (cos² \(\frac{θ}{2}\))A
(b) (cos² \(\frac{θ}{2}\))AT
(c) (cos²θ)I
(d) (sin² \(\frac{θ}{2}\))A
Solution:
(b) (cos² \(\frac{θ}{2}\))AT
Hint:
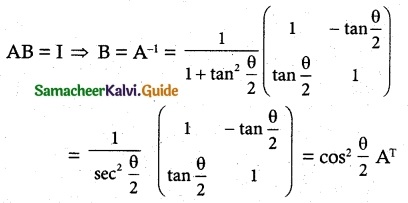
Question 15.
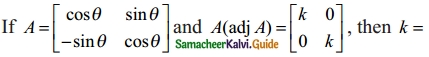
(a) 0
(b) sin θ
(c) cos θ
(d) 1
Solution:
(d) 1
Hint:
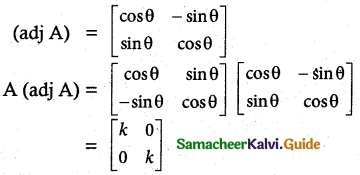
cos² θ + sin² θ = k
Hence k = 1
![]()
Question 16.
If A = \(\begin{bmatrix} 2 & 3 \\ 5 & -2 \end{bmatrix}\) be such that λA-1 = A, then λ is:
(a) 17
(b) 14
(c) 19
(d) 21
Solution:
(c) 19
Hint:
λA-1 = A
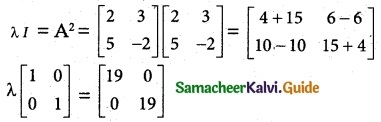
⇒ λ = 19
Question 17.
If adj A = \(\begin{bmatrix} 2 & 3 \\ 4 & 1 \end{bmatrix}\) and adj B = \(\begin{bmatrix} 1 & -2 \\ -3 & 1 \end{bmatrix}\) then adj (AB) is:
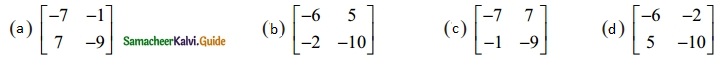
Solution:
(b) \(\begin{bmatrix} -6 & 5 \\ -2 & -10 \end{bmatrix}\)
Hint:
adj (AB) = (adj B) (adj A)
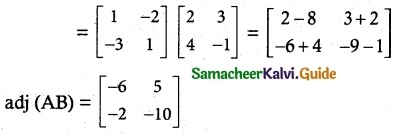
![]()
Question 18.

(a) 1
(b) 2
(c) 4
(d) 4
Solution:
(a) 1
Hint:
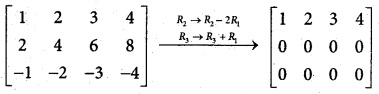
∴ Number of non zero row = 1
ρ(A) = 1
Question 19.
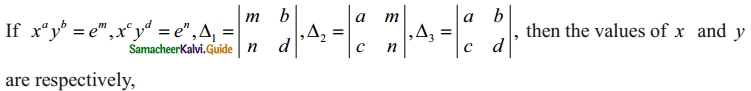
(a) \(e^{(Δ_{2}/Δ_{1})}\), \(e^{(Δ_{3}/Δ_{1})}\)
(b) log(Δ1/Δ3), log(Δ2/Δ3)
(c) log(Δ2/Δ1), log(Δ3/Δ1)
(d) \(e^{(Δ_{1}/Δ_{3})}\), \(e^{(Δ_{2}/Δ_{3})}\)
Solution:
(d) \(e^{(Δ_{1}/Δ_{3})}\), \(e^{(Δ_{2}/Δ_{3})}\)
Hint:
xayb = em
a log x + b log y = m
xcyd = en
c log x + d log y = n

![]()
Question 20.
Which of the following is/are correct?
(i) Adjoint of a symmetric matrix is also a symmetric matrix.
(ii) Adjoint of a diagonal matrix is also a diagonal matrix.
(iii) If A is a square matrix of order n and λ is a scalar, then adj(λA) = λn adj (A).
(iv) A(adj A) = (adj A)A = |A|I
(a) Only (i)
(b) (ii) and (iii)
(c) (iii) and (iv)
(d) (i), (ii) and (iv)
Solution:
(d) (i), (ii) and (iv)
Question 21.
If ρ(A) ρ([A | B]), then the system AX = B of linear equations is:
(a) consistent and has a unique solution
(b) consistent
(c) consistent and has infinitely many solutions
(d) inconsistent
Solution:
(b) consistent
Hint:
If ρ(A) = ρ[A|B] = no. of unknowns
We say consistent an unique solutions
Hence ρ(A) = ρ[A|B] ← given
Question 22.
If 0 ≤ θ ≤ π and the system of equations x + (sin θ)y – (cos θ)z = 0, (cos θ) x – y + z = 0, (sin θ) x + y + z = 0 has a non-trivial solution then θ is:
(a) \(\frac{2π}{3}\)
(b) \(\frac{3π}{4}\)
(c) \(\frac{5π}{6}\)
(d) \(\frac{π}{4}\)
Solution:
(d) \(\frac{π}{4}\)
Hint:
If AX = 0 has non trivial solution if |A| = 0
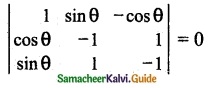
⇒ 1(1 – 1) – sinθ (-cosθ – sinθ) – cosθ (cosθ + sinθ) = 0
⇒ + sinθ cosθ + sin²θ – cos²θ – sinθ cosθ = 0
⇒ sin²θ – cos²θ = 0
⇒ sinθ = cosθ
θ =\(\frac{π}{4}\)
![]()
Question 23.

(a) λ = 7, µ ≠ -5
(b) λ = -7, µ = 5
(c) λ ≠ 7, µ ≠ -5
(d) λ = 7, µ = -5
Solution:
(d) λ = 7, µ = -5
Hint:
ρ(A) = ρ[A | B] = 2
λ – 7 = 0 and µ + 5 = 0
λ = 7, µ = -5
Question 24.
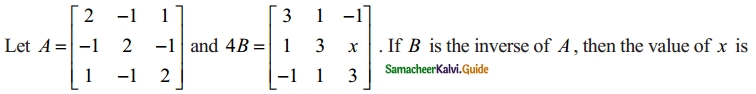
(a) 2
(b) 4
(c) 3
(d) 1
Solution:
(b) 4
Hint:
B = A-1

![]()
Question 25.
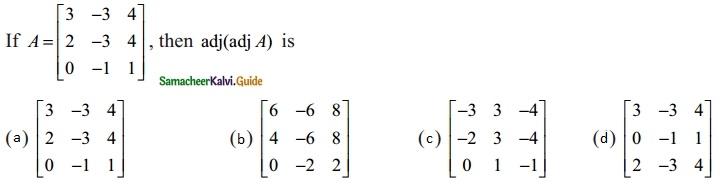
Solution:
(a) \(\left[\begin{array}{rrr}
3 & -3 & 4 \\
2 & -3 & 4 \\
0 & -1 & 1
\end{array}\right]\)
Hint:
adj (adj A) = |A|n-2 A = |A|² A
|A|= 3(-3 + 4) + 3(2) + 4 (-2)
= 3 + 6 – 8
= 1