Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 7 Probability Distributions Miscellaneous Problems Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 7 Probability Distributions Miscellaneous Problems
Question 1.
A manufacturer of metal pistons finds that on the average, 12% of his pistons are rejected because they are either oversize or undersize. What is the probability that a batch of 10 pistons will contain
(a) no more than 2 rejects?
(b) at least 2 rejects?
Solution:
In a binomial distribution
n = 10; p = \(\frac { 12 }{100}\) = \(\frac { 3 }{25}\); q = 1 – p = 1 – \(\frac { 3 }{25}\); q = \(\frac { 22 }{25}\)
p(X = x) = ncxpxqn-x
(a)p(no more than 2 rejects)
p(x ≤ 2) = p(x = 0) + p(x = 1) + p(x = 2)

![]()
(b) p (at least 2 rejects) = p (x ≥ 2)

Question 2.
Hospital records show that of patients suffering from a certain disease 75% die of it. What is the probability that of 6 randomly selected patients, 4 will recover?
Solution:
Let x be the random variable of patience suffering from a certain disease
In a binomial distribution
p (X = x) = ncxpxqn-x

Question 3.
If electricity power failures occur according to a Poisson distribution with an average of 3 failures every twenty weeks, calculate the probability that there will not be more than one failure during a particular week.
Solution:
In a poisson distribution
mean(λ) = \(\frac { 3 }{20}\) = 0.15
p(X = x) = \(\frac { e^{-λ}λ^x }{x!}\)
p(not be more than one failure) = p(x ≤ 1)
p(x = 0) + p(x = 1)
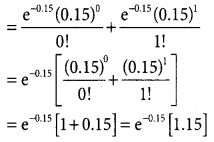
= 0.86074 × (1.15)
= 0.98981
![]()
Question 4.
Vehicles pass through a junction on a busy road at an average rate of 300 per hour.
1. Find the probability that none passes in a given minute.
2. What is the expected number passing in two minutes?
Solution:
In a poisson distribution
Average per hour = 300 vehicles
mean per minute = \(\frac { 300 }{60}\) = 5
∴ λ = 5

= e-5(12.5)
= 0.0067379 × 12.5
= 0.08422375
= 0.08422375 × 10²
![]()
Question 5.
Entry to a certain University is determined by a national test. The scores on this test are normally distributed with a mean of 500 and a standard deviation of 100. Raghul wants to be admitted to this university and he knows that he must score better than at least 70% of the students who took the test. Raghul takes the test and scores 585. Will he be admitted to this university?
Solution:
Let x denotes the scores of a national test mean
µ = 500 and standard deviation σ = 100
standard normal variate z = \(\frac { x-µ }{σ}\) = \(\frac { x-5000 }{100}\)
when x = 585
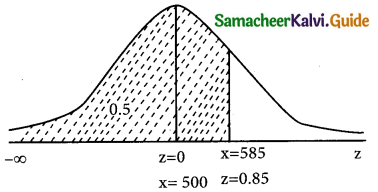
z = \(\frac { 585-500 }{100}\) = \(\frac { 85 }{100}\) = 0.85
p(x ≤ 585) = p(z ≤ 0.85)
p(z ≤ 0.85) = p(-∞ < z < 0) + p(0 < z < 0.85)
= 0.5 + 0.3023
= 0.8023
for n = 100;
p(z ≤ 0.85) = 100 × 0.8023
= 80.23
∴ Raehul scores 80.23%
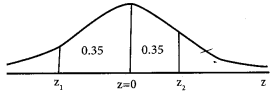
We can determine the scores of 70% of the students as follows:
from the table for the area 0.35
We get z1 = -1.4(as z1 lies to left of z = 0)
similarly z2 = 1.4
Now z1 = \(\frac { x_1-500 }{100}\) ⇒ -1.4 = \(\frac { x_1-500 }{100}\)
-1.4 × 100 = x1 – 500 ⇒ x1 500 – 140
x1 = 360
Again z2 = \(\frac { x_2-500 }{100}\) ⇒ -1.4 = \(\frac { x_1-500 }{100}\)
1.4 × 100 = x2 – 500 ⇒ x2 = 140 + 500
= x2 = 640
Hence 70% of students score between 360 and 640
But Raghul scored 585. His score is not better than the score of 70% of the students.
∴ He will not be admitted to the university.
Question 6.
The time taken to assemble a car in a certain plant is a random variable having a normal distribution of 20 hours and a standard deviation of 2 hours. What is the probability that a car can be assembled at this plant in a period of time.
(i) less than 19.5 hours?
(ii) between 20 and 22 hours?
Solution:
Let x denotes the time taken to assemable cars mean µ = 20 hours and S.D σ = 2 hours
The standard normal variate
z = \(\frac { x-µ }{σ}\) = \(\frac { x-20 }{2}\)
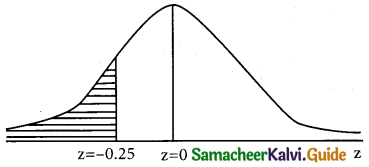
(i) p(less than 19.5 hours) = p(x < 19.5)
when x = 19.5
z = \(\frac { 19.5 }{2}\) = \(\frac { -0.5 }{2}\) = 0.25
p(x < 19.5) = p(z < – 0.25)
= p(-∞ < z < 0) – p(-0.25 < z < 0)
= 0.5 – p(0 < z < 0.25)
= 0.5 – 0.0987
= 0.4013
(ii) p(between 20 and 22 hours) = p(20 < x < 22)
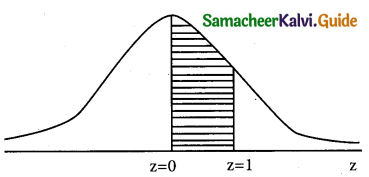
when x = 20
z = \(\frac { 20-20 }{2}\) = \(\frac { 0 }{2}\) = 0
when x = 22;
z = \(\frac { 22-20 }{2}\) = \(\frac { 2 }{2}\) = 1
p(20 < x < 22) = p(0 < z < 1)
= 0.3413
![]()
Question 7.
The annual salaries of employees in a large company are approximately normally distributed with a mean of $50,000 and a standard deviation of $20,000.
(a) What percent of people earn less than $40,000?
(b) What percent of people earn between $45,000 and $65,000?
(c) What percent of people earn more than $75,000
Solution:
Let x denotes the annual salaries of employees in a large company
mean µ = 50,000 and S.D σ = 20,000
Standard normal variate z = \(\frac { x-µ }{σ}\)
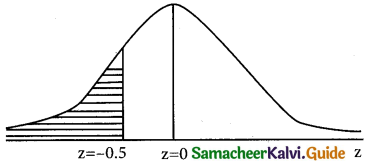
(a) p(people earn less than $40,000) = p(x < 40,000)
when x = 40,000
z = \(\frac { 40,000-50,000 }{20,000}\) = \(\frac { 10,000 }{20,000}\)
z = -0.5
p(x < 40,000) = p(z < -0.5)
= p(-∞ < z < 0) – p(-0.5 < z < 0)
= 0.5 -p(-0.5 < z <0)
= 0.5 – p(0 < z < 0.5) (due to symmetry)
= 0.5 – 0.01915
= 0.3085
= p(x < 40,000) in percentage = 0.3085 × 100 = 30.85
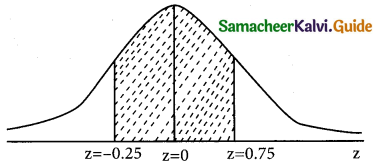
(b) p(people ear between $45,000 and $65,000)
p(45000 < x < 65000)
When x = 45,000;
z = \(\frac { 45,000-50,000 }{20,000}\) = \(\frac { -5000 }{20,000}\) = \(\frac { -1 }{4}\)
z = -0.25
when x = 65,000;
z = \(\frac { 65,000-50,000 }{20,000}\) = \(\frac { 15000 }{20,000}\) = \(\frac { 3 }{4}\)
z = 0.75
p(45000 < x < 65000) = p(-0.25 < z < 0.75)
= p(-0.25 < z < 0) + p(0 < z < 0.75)
= p(0 < z < 0.25) + p(0 < z < 0.75)
= p(0 < z < 0.25) + p(0 < z < 0.75)
= 0.0987 + 0.2734 = 0.3721
p(45000 < x < 65000) in percentage = 0.3721 × 100
= 37.21
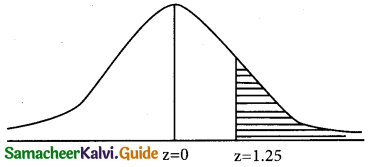
p(people earn more than$75,000) = p(x > 70000)
when x = 75,000;
z = \(\frac { 75,000-50,000 }{20,000}\) = \(\frac { 25000 }{20,000}\) = \(\frac { 5 }{4}\)
z = 1.25
p(x > 75,000) = p(x > 1.25)
= p(0 < z < ∞) – p(0 < z < 1.25) = 0.5 – 0.3944 = 0.1056 p(x > 750,000)in percent = 01056 × 100
= 10.56
![]()
Question 8.
X is a normally normally distributed variable with mean µ = 30 and standard deviation σ = 4. Find
(a) P(x < 40) (b) P(x > 21)
(c) P(30 < x < 35)
Solution:
x is a normally distributed variable with mean µ = 30 and standard deviation σ = 4
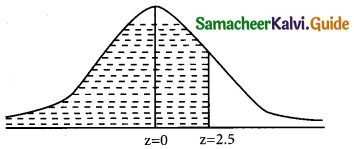
Then the normal variate z = \(\frac { x-µ }{σ}\) = \(\frac { x-30 }{4}\)
(a) p(x < 40) = ?
when x = 40;
z = \(\frac { 40-30 }{4}\) = \(\frac { 10 }{4}\) = 2.5
p(x < 40) = p(z < 2.5)
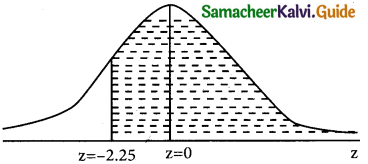
= p(-∞ < z < 0) + p(0 < z < 2.5) = 0.5 + 0.4938 = 0.9938 (b) p(x > 21) = ?
when x = 21;
z = \(\frac { 40-30 }{4}\) = \(\frac { 10 }{4}\) = -2.25
p(x > 21) = p(z > -2.25)
= p(-2.25 < z < 0) + p(0 < z < ∞)
= p(0 < z < 2.25) + 0.5
= 0.4878 + 0.5
= 0.9878
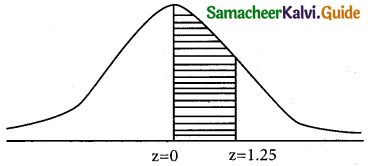
(c) p(30 < x < 35) = ?
when x = 30;
z = \(\frac { 30-30 }{4}\) = \(\frac { 0 }{4}\) = 0
when x = 35;
z = \(\frac { 35-30 }{4}\) = \(\frac { 5 }{4}\) = 1.25
p(30 < x < 35) = p(0 < z < 1.25)
= 0.3944
Question 9.
The birth weight of babies is Normally distributed with mean 3,500 g and standard deviation 500 g. What is the probability that a baby is born that weighs less than 3,100 g?
Solution:
Let x be a normally distributed variable with mean 3,500 g and standard deviation 500 g
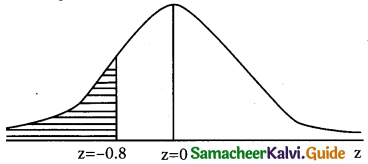
Here µ = 3500 and σ = 500
The standard normal variate z = \(\frac { x-µ }{σ}\)
p(weight less than variate 3100 g) = p(x < 3100)
when x = 3100;
z = \(\frac { 3100-3500 }{500}\) = \(\frac { -400 }{500}\) = \(\frac { -4 }{5}\)
z = -0.8
∴ p(z < 3100) = p(z < -0.8)
= p(-∞ < z < 0) – p(-0.8 < z < 0)
= 0.5 – p(0 < z < 0.8)
= 0.5 – 0.2881
= 0.2119
![]()
Question 10.
People’s monthly electric bills in chennai are normally distributed with a mean of Rs 225 and a standard deviation of Rs 55. Those people spend a lot of time online. In a group of 500 customers, how many would we expect to have a bill that is Rs 100 or less?
Solution:
Let X be a normally distributed variable with a mean of Rs 225 and a standard deviation of Rs 55
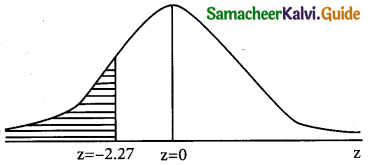
Here µ = 225 and σ = 55
The standard normal variate z = \(\frac { x-µ }{σ}\) = \(\frac { x-225 }{55}\)
p(a bill have Rs 100 or less) = p(x ≤ 100)
when x = 100;
z = \(\frac { 100-225 }{55}\) = \(\frac { -125 }{55}\) = -2.27
p(x ≤ 100) = p(z < -2.27)
p(z < -2.27) = p(-∞ < z < 0) – p(-2.27 < z < 0)
= 0.5 – p(0 < z < 2.27)
= 0.5 – 04884
= 0.0116
![]()