Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 7 Probability Distributions Ex 7.1 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 7 Probability Distributions Ex 7.1
Question 1.
Define Biomial distribution.
Solution:
Binomial distribution was discovered by James Bernoulli (1654-1705) in the year 1700.
A random variable X is said to follow binomial distribution with parameter n and p, if it assumes only non-negative value and its probability mass function in given by
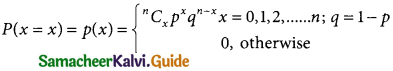
![]()
Question 2.
Define Bernouli trials.
Solution:
A random experiment whose outcomes are of two types namely success S and failure F, occurring with probabilities p and q respectively, is called a Bernoulli trial.
Some examples of Bernoulli trials are:
(i) Tossing of a coin (Head or tail)
(ii) Throwing of a die (getting even or odd number)
Question 3.
Derive the mean and variance of bionomial distribution
Solution:
Derivation of the Mean and Variance of Binomial distribution:
The mean of the binomial distribution
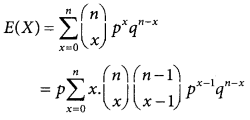
= np(q + p)n – 1 [since p + q = 1]
= np
E(X) = np
The mean of the binomial distribution is np.
Var(X) = E(X²) – E(X²)
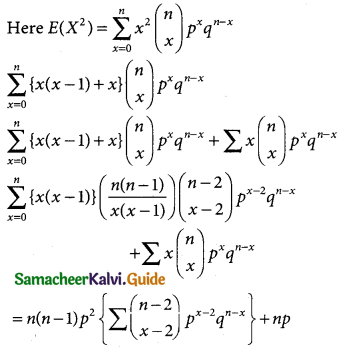
= n(n – 1)p²(q + p)(n – 2) + np
n(n – 1 )p² + np
Variance = E(X²) – [E(X)]²
= n²p² – np² + np – n²p²
= np(1 – p) = npq
Hence, mean of the BD is np and the Variance is npq.
Question 4.
Write down the condition for which the bionomial distribution can be used.
Solution:
The Binomial distribution can be used under the following conditions:
1. The number of trials ‘n finite
2. The trials are independent of each other.
3. The probability of success ‘p’ is constant for each trial.
4. In every trial there are only two possible outcomes – success or failure.
Question 5.
Mention the properties of bionomial distribution.
Solution:
Properties of Binomial distribution
1. Binomial distribution is symmetrical if p = q = 0.5, It is skew symmetric if p ≠ q. It is positively skewed if p < 0.5 and it is negatively skewed it p > 0.5.
2. For Binomial distribution, variance is less than mean
Variance npq = (np) q < np
![]()
Question 6.
If 5% of the items produced turn out to be defective, then find out the probability that out of 10 items selected at random there are
(i) exactly three defectives
(ii) atleast two defectives
(iii) exactly 4 defectives
(iv) find the mean and variance.
Solution:
Probability of getting a defective item
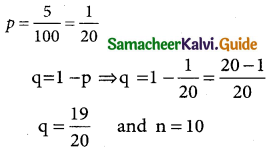
In binomial distribution
p(X = x) = nCxpxqn-x
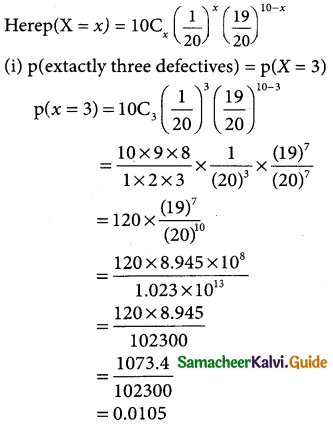
Let x = (19)²
log x = 7 log(19)7
= 7 log 19
= 7 × 1.2788
= 8.9516
x = Antilog 8.956
= 8.945 × 108
ut y = (20)10
log y = (10) log 20
= 10 × 1.3010
= 13.010
y = Anti log 13.010
= 1.023 × 10³
(ii) p(atleast two defectives)
= p(x ≥ 2)
= p(x = 2) = p(x = 3) + ………….. + p(x = 10)
= 1 – p(x < 2)
= 1 – {p(x = 0) + p(x = 1)}

Let x = (19)9
log x = 9 log 19
= 9 × 1.2788
= 11.5092
x = Antilog 11.5092
= 3.229 × 1011
(iii) p(extactly 4 defectives) = p(X = 4)
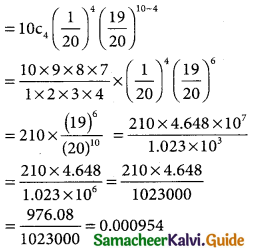
Let x = (19)6
log x = 6 log 19
= 6 × 1.2788
log x = 7.66728
Antilog (7.66728)
x = 4.648 × 107
(iv) mean E(x) = np
= 10 × \(\frac { 1 }{20}\) = \(\frac { 1 }{2}\) = 0.5
Varaince = npq
= 10 × \(\frac { 1 }{20}\) = \(\frac { 19 }{20}\) = \(\frac { 19 }{40}\) = 0.475
![]()
Question 7.
In a particular university 40% of the students are having news paper reading habit. Nine university students are selected to find their views on reading habit. Find the probability that
(i) none of those selected have news paper reading habit
(ii) all those selected have news paper reading habit
(iii) atleast two third have news paper reading habit.
Solution:
let p to the probability of having newspaper reading habit
p = \(\frac { 40 }{100}\) = \(\frac { 2 }{5}\)
q = 1 – p = 1\(\frac { 2 }{5}\) = \(\frac { 5-2 }{5}\) = \(\frac { 3 }{5}\) and n = 9
In the binomial distribution p(x = 4) = ncx pxqn-r
The binomial distribution P(x) = 9cx (\(\frac { 2 }{5}\))x (\(\frac { 3 }{5}\))9-x
(i) p(none of those selected have newspaper reading
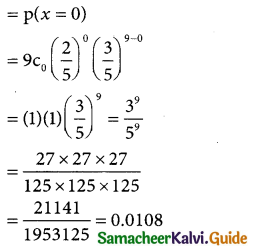
(ii) P(all those selected have newspaper reading habit)
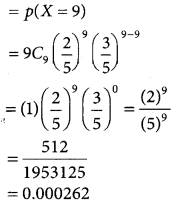
(iii) p(at least two third have newspaper reading habit)
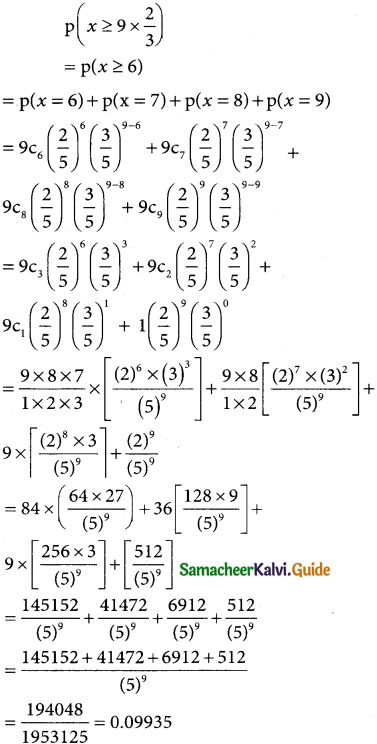
Question 8.
In a family of 3 children, what is the probability that there will be exactly 2 girls?
Solution:
let p be the probability of getting a girl child= 1/2 q = 1 – p ⇒ = 1 – 1/2
∴ q = \(\frac { 1 }{2}\) and n = 3
In a binomial distibution
p(x = x) ncx pxqn-x
p(exactly 2 girls) p(x = 2)
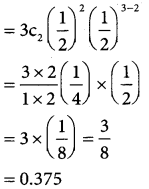
Question 9.
Defects in yarn manufactured by a local mill can be approximated by a distribution with a mean of 1.2 defects for every 6 metres of length. If lengths of 6 metres are to be inspected, find the probability of less than 2 defects.
Solution:
Given n = 6
mean np = 1.2
⇒ 6p = 1.2
p = \(\frac { 1.2 }{6}\) p = 0.2 (or) p = \(\frac { 1 }{5}\)
q = 1 – p = 1 – \(\frac { 1 }{5}\)
∴ q = \(\frac { 4 }{5}\)
The binomial distribution
p(x) = 6Cx (0.2)x(0.8)6-x
p(x < 2) = p(x = 0) + p(x = 1)

![]()
Question 10.
If 18% of the bolts produced by a machine are defective, determine the probability that out of the 4 bolts chosen at random
Solution:
n = 4
probability of defective bolts p = 18/100
9 = 1 – p = 1.018 = 0.82
The binoial distribution p(x) = 4Cx(0.18)x(0.82)4-x
= 4C1(0.18)1(0.82)4-1
= 4 × 0.18 × (0.82)³
= 0.72 × 0.551368
= 0.39698496
p(X = 1)= 0.3969 approximately
(ii) p(none will be defective)p(x = 0)
= 4C0(0.18)°(0.82)4-0
= (1)(1)(0.45212176)
p(x = 0) = 0.45212
(iii) p(almost 2 will be defective) = p(x ≤ 2)
= p(x = 0) + (p(x = 1) + p(x = 2)
= 4C0(0.18)°(0.82)4-0 + 4C1(0.18)1(0.82)4-1 + 4C2 (0.18)² (0.82)4-2
= (0.82)4 + 4 × (0.18) × (0.82)³ + \(\frac { 4×3 }{1×2}\) × (0.18)² (0.82)²
= 0.45212176 + (0.72 × 0.551368) + (6 × 0.0324 × 0.6724)
= 0.45212176 + 0.39698496 + 013071456
= 0.97982128
= 0.9798
Question 11.
If 18% of the bolts produced by a machine are defective, determine the probability that out of the 4 bolts chosen at random
(i) exactly one will be defective
(ii) none will be defective
(iii) atmost 2 will be defective
Solution:
p = 0.09 = \(\frac { 9 }{100}\)
q = 1 – p ⇒ q – 1 – \(\frac { 9 }{100}\)
q = \(\frac { 100-9 }{100}\)
q = \(\frac { 91 }{100}\)
In a binomial distribution p(x = x) = ncxpxqn-x
p(atleast one success) = p(x ≥ 1)

Taking log on both sides log ≤ (0.66) ≤ n log(0.91)
∴ n ≥ log \(\frac { log(0.66) }{log(0.91)}\)
n ≥ 5
∴ 5 or more trials are needed
![]()
Question 12.
Among 28 professors of a certain department, 18 drive foreign cars and 10 drive local made cars. If 5 of these professors are selected at random, what is the probability that atleast 3 of them drive foreign cars?
Solution:
Let p be the probability of foreign cars driven by the professors
p = \(\frac { 18 }{28}\) = \(\frac { 9 }{14}\)
Let q be the probability of local made cars driv¬en by the professors
q = \(\frac { 10 }{28}\) = \(\frac { 5 }{14}\)
and n = 5
The binomial distribution p(x = x) = ncxpxqn-x
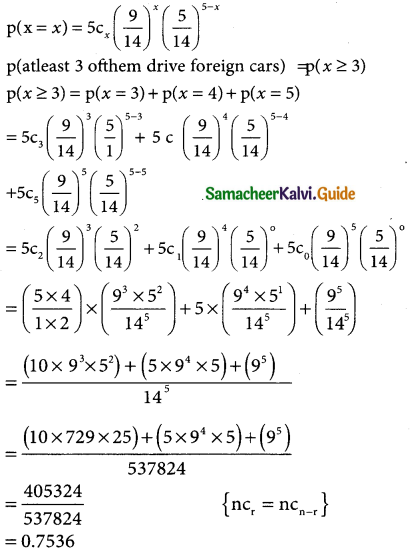
Question 13.
Out of 750 families with 4 children each, how many families would be expected to have (i) atleast one boy (ii) atmost 2 girls (iii) and children of both sexes? Assume equal probabilities for boys and girls?
Solution:
Assume equal probabilities for boys girls let p be the probability of having a boy Let x be the random variable for getting either a boy or a girl
∴ p = \(\frac { 1 }{2}\) and q \(\frac { 1 }{2}\) and n = 4
In binomial distribution p(x = 4) = ncxpxqn-x
Here the binomial distribution is p(X= x)
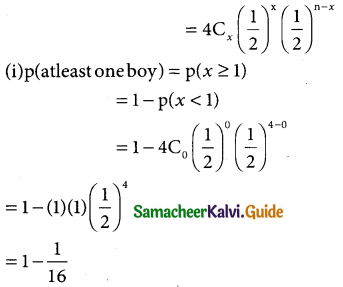
= 1 – 0.0625
= 0.9375
for 750 families (p ≥ 1) = 750 × 0.9375
= 703.125
= 703(approximately)
(ii) p(almost 2 girls) = p(x ≤ 2)
= p(x = 0) = p(x = 1) + p(x = 2)
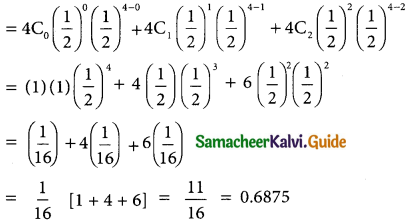
For 750 families p(x ≤ 2) = 0.6875 × 750
= 515.625
= 516 (approximately)
(iii) p(children of both sexes) = p(x = 1) + p(x = 2)p(x = 3)
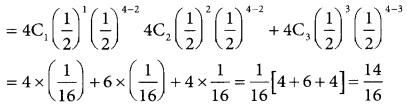
= 0.875 x 750
For 750 families p(x = 2) = 0.875 × 750
= 656.25
= 656 (approximately)
![]()
Question 14.
Forty percent of business travellers carry a laptop. In a sample of 15 business travelers,
Solution:
Given n = 5
p = \(\frac { 40 }{100}\) = \(\frac { 2 }{5}\)
q = 1 – p = 1 – \(\frac { 2 }{5}\) \(\frac { 5-2 }{5}\) = \(\frac { 3 }{5}\)
The binomial distributionp (X = x) = 15cx (\(\frac { 2 }{5}\))x (\(\frac { 3 }{5}\))15-x
(i) p(probability that 3 will have a laptop) = p(x = 3)

(ii) p(12 of the traels will not have a laptop)
= 1 – p(x = 12)
= 1 – 15c12 (\(\frac { 2 }{5}\))12 (\(\frac { 3 }{5}\))15-12

(iii) p(at least three of the travelers have a laptop)
= p(x ≥ 3)
p(x ≥ 3) = 1 – p (x < 3)
= 1 – [p(x = 0) + p(x = 1) + p(x = 2)]
p(x < 3) = p(x = 0) + p(x = 1) + p(x = 2)

Question 15.
A pair 5f dice is thrown 4 times. If getting a doublet is considered a success, find the probability of 2 successes.
Solution:
In a throw of a pair dice the doublets are (1, 1),(1, 2) (3, 3),(4, 4),(5, 5),(6, 6)
probability of getting a doublet p = \(\frac { 6 }{36}\) = \(\frac { 1 }{6}\)
⇒ q = 1 – q = \(\frac { 5 }{6}\) and n = 4 is given
The probability of success = \(\left[\begin{array}{l}
4 \\
x
\end{array}\right]\) [latex]\frac { 1 }{6}[/latex]x [latex]\frac { 5 }{6}[/latex]4-x
Therefore the probability of 2 success are

Question 16.
The mean of a binomial distribution is 5 and standard deviation is 2. Determine the distribution.
Solution:
In a binomial distribution
mean np = 5 → (1)
Standard deviation \(\sqrt { npq}\) = 2
squaring on body sides
npq = 4 → (2)

n = 5 × 5 ⇒ n = 25
∴ the binomial distribution is
P(X = x) = ncxpxqn-x
(i.e) p(X = x) = \(\left[\begin{array}{l}
25 \\
x
\end{array}\right]\) (\(\frac { 1 }{5}\))x (\(\frac { 4 }{5}\))(25-x)
![]()
Question 17.
Determine the binomial distribution for which the mean is 4 and variance 3. Also find P(X = 15)
Solution:
In a binomial distribution
mean np = 4 → (1)
variance npq = 3 → (2)

n = 4 × 4 ⇒ n = 16
The binomial distribution is p(X = x)ncxpxqn-x
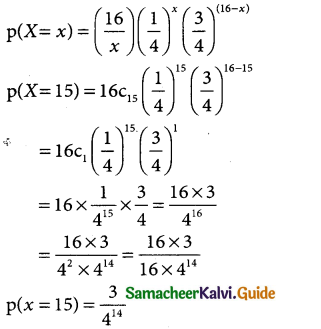
Question 18.
Assume that a drug causes a serious side effect at a rate of three patients per one hundred. What is the probability that atleast one person will have side effects in a random sample of ten patients taking the drug?
Solution:
Here n = 10

= 0.5344
![]()
Question 19.
Consider five mice from the same litter, all suffering from Vitamin A deficiency. They are fed a certain dose of carrots. The positive reaction means recovery from the disease.
Assume that the probability of recovery is 0.73. What is the probability that atleast 3 of the 5 mice recover.
Solution:
n = 5
Let probability of recovery p = 0.73
q = 1 – p = 1 – 0.73
∴ q = 0.27
The binomial distribution is
p (x = x) = nCxpxqn-x
p(x = x) = 5Cx(0.73)x(0.27)5-x
p(atleast 3 of the 5 mice recover) = p(x ≥ 3)
= p(x = 3) + p(x = 4) + p(x = 5)
= 5C3 (0.73)³(0.27)5-3 + 5C4 (0.73)4 (0.27)5-4 + 5C5 (0.73)5 (0.27)5-5
5C2 (0.73)³ (0.27)² + 5c1 (0.73)4 (0.27)1 + 5c0(0.73)5(0.27)°
[\(\frac { 5×4 }{1×2}\) × 0.389017 × 0.0729] + [5 × 0.28398241 × 0.27] + (1 × 0.2073071593 × 1)
= 0.283593393 + 0.3833762535 + 0.2073071593
= 0.2836 + 0.3834 + 0.2073
= 0.8743
Question 20.
Consider five mice from the same litter, all suffering from Vitamin A deficiency. They are fed a certain dose of carrots. The positive reaction means recovery from the disease. Assume that the probability of recovery is 0.73. What is the probability that atleast 3 of the 5 mice recover.
Solution:
Success = 2 × fails
p = 2q ⇒ p = 2(1 – p)
p = 2 – 2p ⇒ p + 2p = 2
3p = 2 and p = 2/3
q = 1 – p = 1 – 2/3
q = 1/3 and n = 5
The binomial destribution is
p (X = x) = nCxpxqn-x
= 5C(2/3)x (1/3)
(i) p(three successes) = p(x = 3)

![]()