Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 6 Random Variable and Mathematical Expectation Ex 6.2 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 6 Random Variable and Mathematical Expectation Ex 6.2
Question 1.
Find the expected value for the random variable of an unbiased die
Solution:
When a un based die is thrown , any one of the number 1, 2, 3, 4, 5, 6, can turn up that x denote the random variable taking the values from 1 to 6
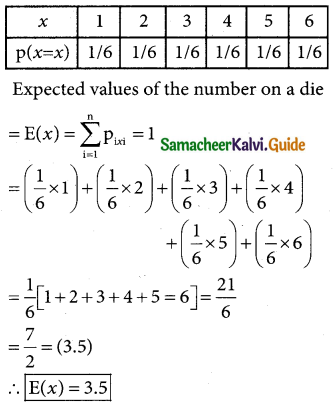
![]()
Question 2.
Let X be a random variable defining number of students getting A grade. Find the expected value of X from the given table
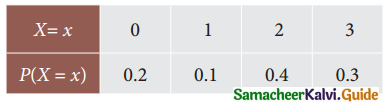
Solution:
Let X be a random variable taking values 0, 1, 2, 3,
Expected value E(x) = Σp1x1
= (0.2 × 0) + (0.1 × 1) + (0.4 × 2) + (0.3 × 3)
= 0 + 0.1 + 0.8 + 0.9
∴ E(x) = 0.18
Question 3.
The following table is describing about the probability mass function of the random variable X
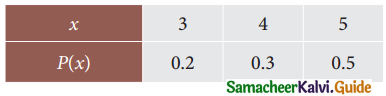
Find the standard deviation of x.
Solution:
Let x be the random variable taking the values 3, 4, 5
E(x) = Σpixi
= (0.1 × 3) + (0.1 × 4) + (0.2 × 5)
0.3 + 0.4 + 1.0
E(x) = 1.7
E(x²) = Σpixi²
= (0.1 × 3²)+ (0.1 × 4²) + (0.2 × 5²)
= (0.1 × 9) + (0.1 × 16) + (0.2 × 25)
E(x²) = 7.5
Var(x) = E(x²) – (E(x)]²
= 7.5 – (1.7)²
= 7.5 – 2.89
Var(x) = 4.61
Standard deviation(S.D) = \(\sqrt { var (x)}\)
= \(\sqrt { 4.61}\)
σ = 2.15
Question 4.
Let X be a continuous random variable with probability density function
fx (x) = \(\left\{\begin{array}{l}
2 x, 0 \leq x \leq 1 \\
0, \text { otherwise }
\end{array}\right.\)
Find the expected value of X.
Solution:
Let x be a continuous random variable. In the probability density function, Expected
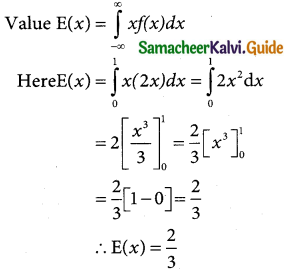
![]()
Question 5.
Let X be a continuous random variable with probability density function
fx (x) = \(\left\{\begin{array}{l}
2 x, 0 \leq x \leq 1 \\
0, \text { otherwise }
\end{array}\right.\)
Find the mean and variance of X.
Solution:
Let x be a continuous random variable. In the probability density function,


Question 6.
In an investment, a man can make a profit I of ₹ 5,000 with a probability of 0.62 or a loss of ₹ 8,000 with a probability of 0.38 . Find the expected gain.
Solution:
| X | 5000 | -8000 |
| P(x = x) | 0.62 | 0.38 |
Let x be the random variable of getting gain in an Investment
E(x) be the random variable of getting gain in an Investment
E(x) = ΣPixi
= (0.62 × 5000) + [0.38 × (-8000)]
= 3100 – 3040
E(x) = 60
∴ Expected gain = ₹ 60
Question 7.
What are the properties of mathematical expectation?
Properties of Mathematical expectation
Solution:
i. E(a) = a, where ‘a’ is a constant.
ii. E(aX) = aE(X)
iii. E(aX + b) = aE(X) + b, where ‘a’ and ‘b’ are constants.
iv. If X ≥ 0, then E(X) ≥ 0
v. V(a) = 0
vi. If X is random variable, then V(aX + b) = a²V(X)
![]()
Question 8.
What do you understand by mathematical expectation?
Solution:
The average value of a random Phenomenon is termed as mathematical expectation or expected value.
The expected value is weighted average of the values of a random variable may assume
Question 9.
How do you define variance in terms of Mathematical expectation?
Solution:
The variance of X is defined by
Var(X) = Σ[x – E(X)]² p(x)
If X is discrete random variable with probability mass function p(x).
Var(X) = \(\int_{ -∞ }^{∞}\) [x- E(X)]² fx (x) dx
If X is continuous random variable with probability density function fx (x).
Question 10.
Define mathematical expectation in tears of discrete random variable?
Solution:
Let X be a discrete random variable with probability mass function (p.m.f.) p(x). Then, its expected value is defined by
E(X) = \(\sum_{ x }\) x p(x) ……(1)
Question 11.
State the definition of mathematical expectation using continous random variable.
Solution:
If X is a continuous random variable and fix) is the value of its probability density function at x, the expected value of X is
E(X) = \(\int_{ -∞ }^{∞}\) x f(x) dx …….(2)
![]()
Question 12.
In a business venture a man can make a profit of ₹ 2,000 with a probability of 0.4 or have a loss of ₹ 1,000 with a probability of 0.6. What is his expected, variance and standard deviation of profit?
Solution:
Let X be the random variable of getting profit in a business
| X | 2000 | -1000 |
| P(x = x) | 0.4 | 0.6 |
E(x) = Σxxpx(x)
= (0.4 × 2000) +[0.6 × (-1000)]
= 800 – 600
E(X) = 200
∴ Expected value of profit = ₹ 200
E(X²) = Σx² Px(x)
= [(2000)² × 0.4] + [(-1000)² × 0.6]
= (4000000 × 0.4) + (1000000 × 0.6)
E(X²) = 2200000
Var(X) = E(X²) – [E(X)]²
= 22000000 – (200)²
= 2200000 – 40000
Var(X) = 21,60,000
Variance of his profit = ₹ 21,60,000
Standard deviation(S.D) = \(\sqrt { var (x)}\)
σ = \(\sqrt { 2160000}\)
σ = 1469.69
Standard deviation of his profit is ₹ 1,469.69
Question 13.
The number of miles an automobile tire lasts before it reaches a critical point in tread wear can be represented by a p.d.f.
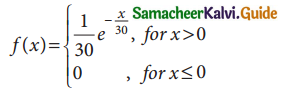
Find the expected number of miles (in thousands) a tire would last until it reaches the critical tread wear point.
Solution:
We know that,

![]()
Question 14.
A person tosses a coin and is to receive ₹ 4 for a head and is to pay ₹ 2 for a tail. Find the expectation and variance of his gains.
Solution:
Let X denote the amount the person receives in a game
Then X takes values 4,-2 and
So P(X = 4) = P (of getting a head)
= \(\frac { 1 }{2}\)
P(X = – 2) = P (of getting a tail)
= \(\frac { 1 }{2}\)
Hence the Probability distribution is
| X | 4 | -2 |
| P(x = x) | 1/2 | 1/2 |
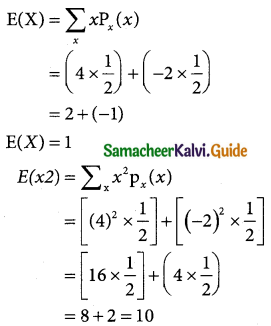
E(x²) = 10
Var(x) = E(x²) – E(x²)
= 10 – (1)²
Var(x) = 9
∴ His expected gain = ₹ 1
His variance of gain = ₹ 9
Question 15.
Let X be a random variable and Y = 2X + 1. What is the variance of Y if variance of X is 5?
Solution:
Var(X) = 5
Var(Y) = var (2x + 1) {∴ v(ax + b) = a²v(x)}
= (2)² var(X)
= 4(5)
Var() = 20
![]()