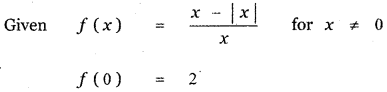Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 9 Limits and Continuity Ex 9.6 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 9 Limits and Continuity Ex 9.6
Choose the correct or the most suitable answer
Question 1.
![]()
(1) 1
(2) 0
(3) ∞
(4) -∞
Answer:
(2) 0
Explaination:
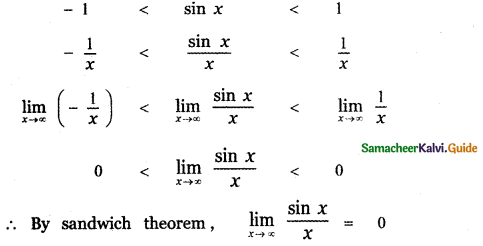
![]()
Question 2.
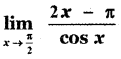
(1) 2
(2) 1
(3) -2
(4) 0
Answer:
(3) -2
Explaination:

![]()
Question 3.
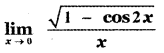
(1) 0
(2) 1
(3) √2
(4) does not exist
Answer:
(3) √2
Explaination:
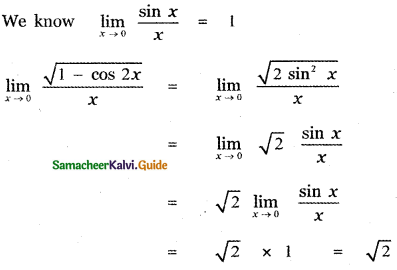
Question 4.
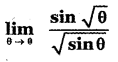
(1) 1
(2) -1
(3) 0
(4) 2
Answer:
(1) 1
Explaination:

![]()
Question 5.
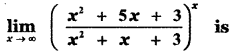
(1) e4
(2) e2
(3) e3
(4) 1
Answer:
(1) e4
Explaination:
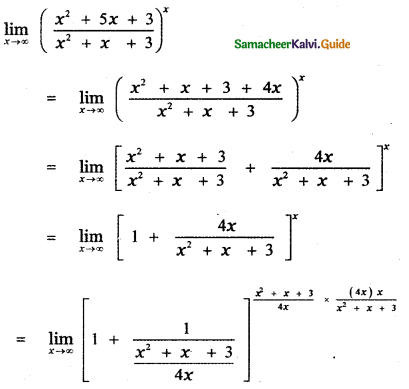
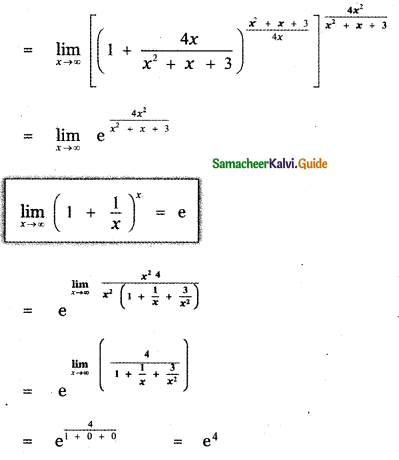
![]()
Question 6.
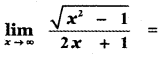
(1) 1
(2) 0
(3) -1
(4) \(\frac{1}{2}\)
Answer:
(4) \(\frac{1}{2}\)
Explaination:

![]()
Question 7.
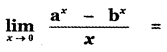
(1) log ab
(2) log \(\left(\frac{\mathbf{a}}{\mathbf{b}}\right)\)
(3) log \(\left(\frac{\mathbf{b}}{\mathbf{a}}\right)\)
(4) \(\frac{\mathbf{a}}{\mathbf{b}}\)
Answer:
(2) log \(\left(\frac{\mathbf{a}}{\mathbf{b}}\right)\)
Explaination:

Question 8.
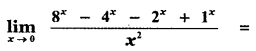
(1) 2 log 2
(2) 2(log 2)2
(3) log 2
(4) 3 log 2
Answer:
(2) 2(log 2)2
Explaination:

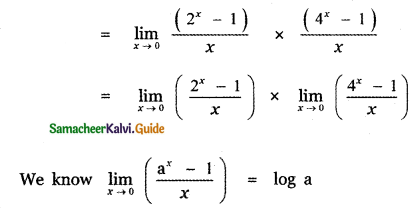
= (log 2) × (log 4)
= log 2 × log 22
= log 2 × 2 log 2
= 2 (log 2)2
![]()
Question 9.
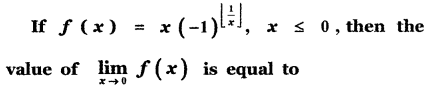
(1) -1
(2) 0
(3) 2
(4) 4
Answer:
(2) 0
Explaination:

![]()
Question 10.
![]()
(1) 2
(2) 3
(3) does not exist
(4) 0
Answer:
(3) does not exist
Explaination:
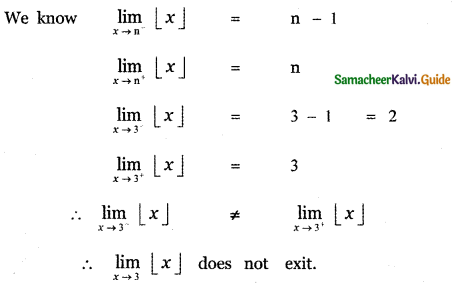
Question 11.
Let the function f be defined by
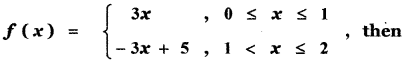
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
Answer:
(4) ![]()
Explaination:

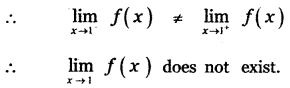
![]()
Question 12.
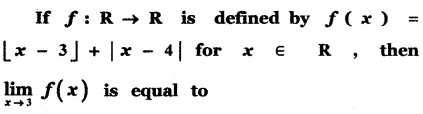
(1) -2
(2) -1
(3) 0
(4) 1
Answer:
(3) 0
Explaination:
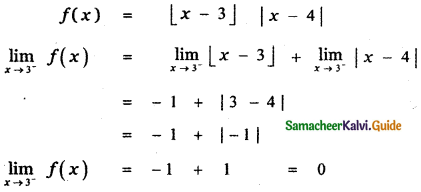
Question 13.
![]()
(1) 1
(2) 2
(3) 3
(4) 0
Answer:
(4) 0
Explaination:
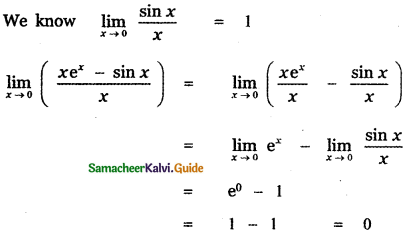
![]()
Question 14.
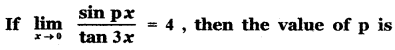
(1) 6
(2) 9
(3) 12
(4) 4
Answer:
(3) 12
Explaination:

![]()
Question 15.
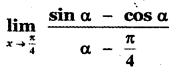
(1) \(\sqrt{2}\)
(2) \(\frac{1}{\sqrt{2}}\)
(3) 1
(4) 2
Answer:
(1) \(\sqrt{2}\)
Explaination:
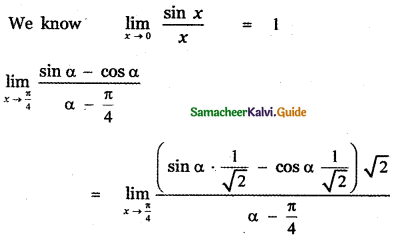
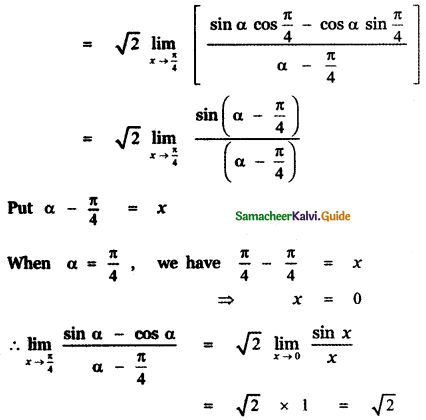
Question 16.
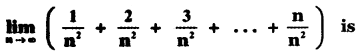
(1) \(\frac{1}{2}\)
(2) 0
(3) 1
(4) ∞
Answer:
(1) \(\frac{1}{2}\)
Explaination:

![]()
Question 17.
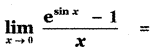
(1) 1
(2) e
(3) \(\frac{1}{\mathrm{e}}\)
(4) 0
Answer:
(1) 1
Explaination:

Question 18.
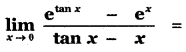
(1) 1
(2) e
(3) \(\frac{1}{2}\)
(4) 0
Answer:
(1) 1
Explaination:
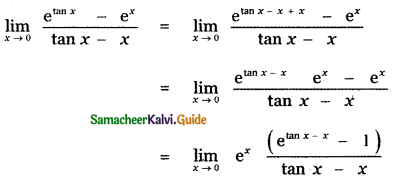
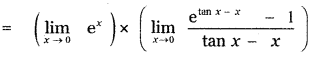
Put tan x – x = y
When x = 0, tan 0 – 0 = y
0 = y
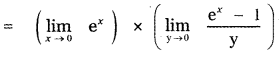
= e0 × 1 = 1 × 1 = 1
![]()
Question 19.
The value of 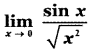 is
is
(1) 1
(2) -1
(3) 0
(4) ∞
Answer:
(1) 1
Explaination:
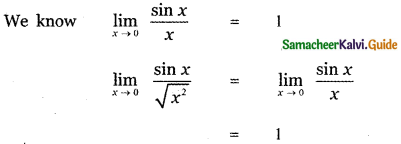
Question 20.
The value of ![]() , where k is an integer is
, where k is an integer is
(1) -1
(2) 1
(3) 0
(4) 2
Answer:
(2) 1
Explaination:
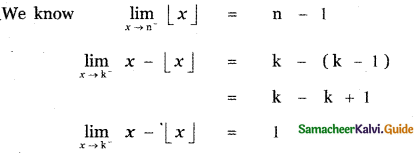
![]()
Question 21.
At x = \(\frac{3}{2}\) the function f(x) = \(\frac{|2 x-3|}{2 x-3}\) is
(1) continuous
(2) discontinuous
(3) differentiable
(4) non zero
Answer:
(2) discontinuous
Explaination:
f(x) = \(\frac{|2 x-3|}{2 x-3}\)
f(x) is not defined at x = \(\frac{3}{2}\)
∴ f(x) is discontinuous at x = \(\frac{3}{2}\)
Question 22.
Let f : R → R be defined by
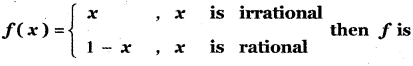
(1) discontinuous x = \(\frac{1}{2}\)
(2) continuous x = \(\frac{1}{2}\)
(3) continuous everywhere
(4) discontinuous everywhere
Answer:
(2) continuous x = \(\frac{1}{2}\)
Explaination:
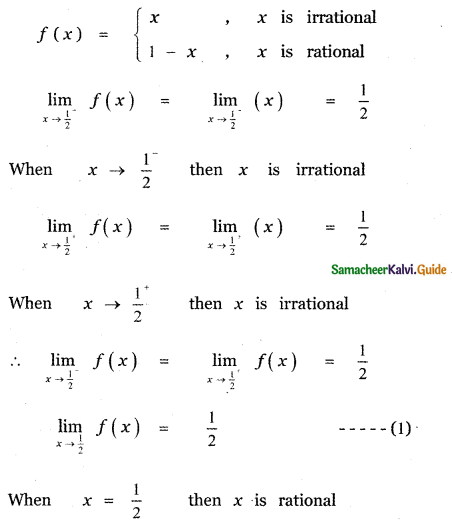

![]()
Question 23.

(1) \(\frac{2}{3}\)
(2) –\(\frac{2}{3}\)
(3) 1
(4) 0
Answer:
(2) –\(\frac{2}{3}\)
Explaination:
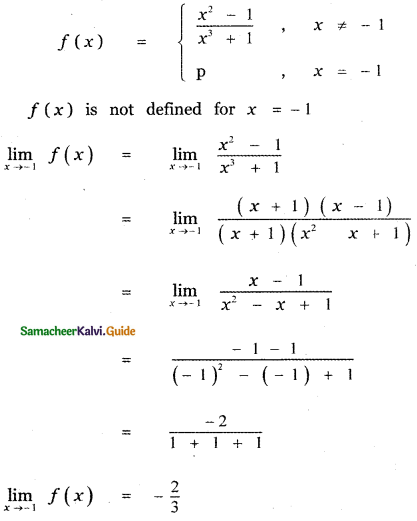
At = -1, f(x) has a removable discontinuity Redefining f(x) as
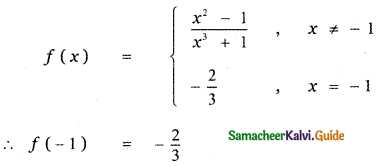
Question 24.
Let f be a continuous function on [2, 5]. If f takes only rational values for all x and f(3) = 12, then f (4.5) is equal to
(1) 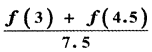
(2) 12
(3) 17.5
(4) 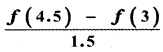
Answer:
(2) 12
Explaination:
Given f(3) = 12
f takes only rational values
f(x) = 12
f(3) = 12
f(4.5) = 12
![]()
Question 25.
Let a function f be defined by f(x) = \(\) for x ≠ 0 and f(0) = 2. Then f is
(1) continuous nowhere
(2) continuous everywhere
(3) continuous for all x except x = 1
(4) continuous for all x except x = 0
Answer:
(4) continuous for all x except x = 0
Explaination: