Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 2 Basic Algebra Ex 2.8 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.8
Question 1.
Find all values of x for which \(\frac{x^{3}(x-1)}{x-2}\) > 0
Answer:
The given inequality is f(x) = \(\frac{x^{3}(x-1)}{x-2}\) > 0
[The critical numbers of f(x) are those values of x for which f(x) = 0, and those values of x for which f(x) is not defined.
When x = 2 , f(x) = ∞ ⇒ f(x) is not defined.]
The critical numbers are x = 0, 1, 2
Divide the number line into 4 intervals
(- ∞, 0), (0, 1), (1, 2) and (2, ∞)
![]()
![]()
(1) (- ∞, 0)
When x < 0 say x = – 1
The factor x3 = (- 1)3 = – 1 < 0
The factor x – 1 = – 1 – 1 = – 2 < 0
The factor x – 2 = – 1 – 2 = – 3 < 0
∴ \(\frac{x^{3}(x-1)}{x-2}\) < 0
Thus \(\frac{x^{3}(x-1)}{x-2}\) > 0 is not true in the interval (- ∞, 0)
Therefore, it has no solution in the interval (- ∞, 0)
(2) (0, 1)
When 0 < x < 1 say x = 0.5
The factor x3 = (0.5 )3 > 0
The factor x – 1 = 0.5 – 1 = – 0.5 < 0
The factor x – 2 = 0.5 – 2 = – 1.5 < 0
Thus x3 > 0, x – 1 < 0 and x – 2 < 0
∴ \(\frac{x^{3}(x-1)}{x-2}\) > 0
Thus \(\frac{x^{3}(x-1)}{x-2}\) > 0 is true in the interval (0, 1)
Therefore it has solution in (0,1)
(3) (1, 2)
When 1 < x < 2 say x = 1.5
The factor x3 = 0
The factor x – 1 = 1.5 – 1 = 0.5 > 0
The factor x – 2 = 1.5 – 2 = – 0.5 < 0
Thus x3 > 0, x – 1 > 0 and x – 2 < 0
∴ \(\frac{x^{3}(x-1)}{x-2}\) < 0
Thus \(\frac{x^{3}(x-1)}{x-2}\) > 0 is not true in the interval (1, 2).
Therefore it has no solution in (1, 2).
![]()
(4) (2, ∞)
When x > 2 say x = 3
The factor x3 = 33 > 0
The factor x – 1 = 3 – 1 = 2 > 0
The factor x – 2 = 3 – 2 = 1 > 0
Thus x3 > 0, x – 1 > 0 and x – 2 > 0
∴ \(\frac{x^{3}(x-1)}{x-2}\) > 0
Thus \(\frac{x^{3}(x-1)}{x-2}\) > 0 is true in the interval (2, ∞).
Therefore it has a solution in (2, ∞)

∴ \(\frac{x^{3}(x-1)}{x-2}\) > 0 has solution in the intervals (0, 1) and (2, ∞)
∴ The solution set is given by (0, 1) ∪ (2, ∞)
![]()
![]()
Question 2.
Find all values of x that satisfies the inequality \(\frac{2 x-3}{(x-2)(x-4)}\) < 0.
Answer:
The given inequality is
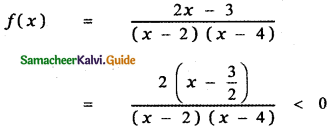
[The critical numbers of f(x) are those values of x for which f(x) = 0, and those values of x for which f(x) is not defined. When x = 2, f(x) = ∞ ⇒ f(x) is not defined.]
The critical numbers are x = \(\frac{3}{2}\), x = 2 , x = 4
Divide the number into 4 intervals
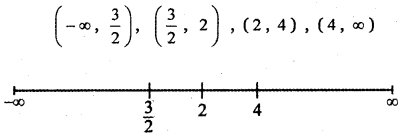
![]()
(1) \(\left(-\infty, \frac{3}{2}\right)\)
When x < \(\frac{3}{2}\) say x = 0
The factor x – \(\frac{3}{2}\) = 0 – \(\frac{3}{2}\) < 0
The factor x – 2 = 0 – 2 < 0
The factor x – 4 = 0 – 4 < 0
Thus x – \(\frac{3}{2}\) < 0, x – 2 < 0 and x – 4 < 0
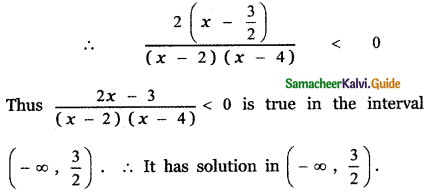
(2) \(\left(\frac{3}{2}, 2\right)\)

![]()
(3) (2, 4)
When 2 < x < 4 say x = 3 The factor x – \(\frac{3}{2}\) = 3 – \(\frac{3}{2}\) = \(\frac{3}{2}\) > 0
The factor x – 2 = 3 – 2 = 1 > 0
The factor x – 4 = 3 – 4 = – 1 < 0 Thus x – \(\frac{3}{2}\) > 0, x – 2 > 0 and x – 4 < 0
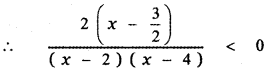
Thus \(\frac{2 x-3}{(x-2)(x-4)}\) < 0 is true in the interval (2, 4) ∴ It has solution in (2, 4). (4) (4, ∞) When x > 4 say x = 5
The factor x – \(\frac{3}{2}\) = 5 – \(\frac{3}{2}\) = \(\frac{7}{2}\) > 0
The factor x – 2 = 5 – 2 = 3 >0
The factor x – 4 = 5 – 4 = 1 > 0
Thus x – \(\frac{3}{2}\) > 0, x – 2 > 0 and x – 4 > 0
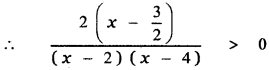
Thus \(\frac{2 x-3}{(x-2)(x-4)}\) < 0 is not true in the interval (4, ∞)
∴ It has a solution in (4, ∞)

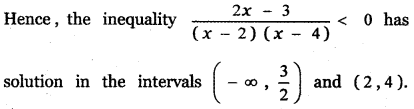
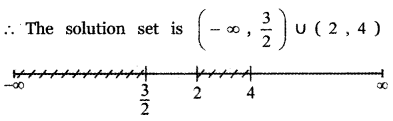
![]()
Question 3.
Solve: \(\frac{x^{2}-4}{x^{2}+4 x-15}\) ≤ 0
Answer:
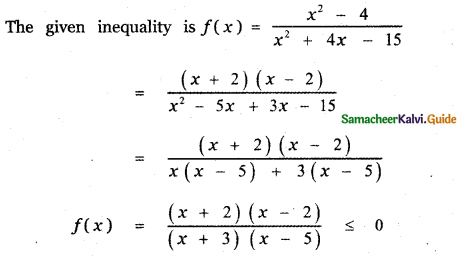
[The critical numbers of f(x) are those values of x for which f(x) = 0, and those values of x for which f(x) is not defined. When x = – 3, 5. f(x) = ∞ ⇒ f(x) is not defined.]
The critical numbers are x = – 2 , 2, – 3, 5
Divide the number line into five intervals
(- ∞, – 3), (- 3, – 2), (- 2, 2), (2, 5) ,(5, ∞)
![]()
![]()
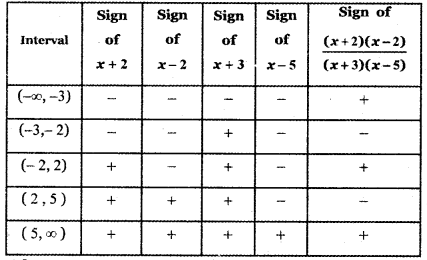
(a) (- ∞, – 3)
When x <- 3 say x = – 4
The factor x + 2 = – 4 + 2 = – 2 < 0
The factor x – 2 = – 4 – 2 = 6 < 0
The factor x + 3 = – 4 + 3 = – 1 < 0
The factor x – 5 = – 4 – 5 = – 9 < 0
Thus x + 2 < 0, x + 3 < 0, x – 2 < 0, x – 5 < 0
∴ \(\frac{x^{2}-4}{x^{2}+4 x-15}\) > 0
Thus \(\frac{x^{2}-4}{x^{2}+4 x-15}\) ≤ 0 is not true in the interval (- ∞, – 3).
∴ It has no solution in (- ∞, – 3)
(b) (- 3, – 2)
When – 3 < x ≤ – 2 say x = – 2.5
The factor x + 2 = – 2.5 + 2 = – 0.5 < 0
The factor x – 2 = – 2.5 – 2 = – 4.5 < 0 The factor x + 3 = – 2.5 + 3 = 0.5 > 0
The factor x – 5 = – 2.5 – 5 = – 7.5 < 0
Thus x + 2 < 0, x + 3 > 0
and
x – 2 < 0
x – 5 < 0
∴ \(\frac{x^{2}-4}{x^{2}+4 x-15}\) < 0
Thus \(\frac{x^{2}-4}{x^{2}+4 x-15}\) ≤ 0 is not true in the interval (- 3, – 2).
∴ It has no solution in (- 3, – 2)
![]()
(c) (-2, 2)
When – 2 ≤ x ≤ 2 say x = 0
The factor x + 2 = 0 + 2 = 2 > 0
The factor x – 2 = 0 – 2 = – 2 < 0
The factor x + 3 = 0 + 3 = 3 > 0
The factor x – 5 = 0 – 5 = – 5 < 0
Thus x + 2 > 0 ,
x + 3 > 0
and
x – 2 < 0
x – 5 < 0
∴ \(\frac{x^{2}-4}{x^{2}+4 x-15}\) > 0
Thus \(\frac{x^{2}-4}{x^{2}+4 x-15}\) ≤ 0 is not true in the interval (- 2, – 2).
∴ It has no solution in (- 2, – 2)
(d) (2, 5)
When 2 ≤ x < 5 say x = 3 The factor x + 2 = 3 = 3 + 2 = 5 > 0
The factor x – 2 = 3 – 2 = 1 > 0
The factor x + 3 = 3 + 3 = 6 > 0
The factor x – 5 = 3 – 5 = – 2 < 0 Thus x + 2 > 0,
x + 3 > 0
and
x – 2 > 0
x – 5 < 0
∴ \(\frac{x^{2}-4}{x^{2}+4 x-15}\) < 0
Thus \(\frac{x^{2}-4}{x^{2}+4 x-15}\) ≤ 0 is not true in the interval (2, 5).
∴ It has no solution in (2, 5)
![]()
(e) (5, ∞)
When 5 < x < ∞ say x = 6 The factor x + 2 = 6 + 2 = 8 > 0
The factor x – 2 = 6 – 2 = 4 > 0
The factor x + 3 = 6 + 3 = 9 > 0
The factor x – 5 = 6 – 5 = 1 > 0
Thus
x + 2 > 0,
x + 3 > 0
and
x – 2 > 0,
x – 5 > 0
∴ \(\frac{x^{2}-4}{x^{2}+4 x-15}\) > 0
Thus \(\frac{x^{2}-4}{x^{2}+4 x-15}\) ≤ 0 is not true in the interval (5, ∞).
∴ It has no solution in (5, ∞)
The given inequality f(x) = \(\frac{x^{2}-4}{x^{2}+4 x-15}\) ≤ 0 has solution in the intervals (-3, – 2]
∴ The solution set is (-3, 2] ∪ [2, 5)
![]()