Students can Download Samacheer Kalvi 10th Maths Model Question Paper 2 English Medium Pdf, Samacheer Kalvi 10th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamil Nadu Samacheer Kalvi 10th Maths Model Question Paper 2 English Medium
Instructions
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- All questions of Part I, II, III and IV are to be attempted separately.
- Question numbers 1 to 14 in Part I are Multiple Choice Quèstions of one-mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and.writing the option code and the corresponding answer.
- Question numbers 15 to 28 in Part II àre two-marks questions. These are to be answered in about one or two sentences.
- Question numbers 29 to 42 in Part III are five-marks questions. These are to be answered in about three to five short sentences.
- Question numbers 43 to 44 in Part IV are eight-marks questions. These are to be answered in detail. Draw diagrams wherever necessary.
Time: 3 Hours
Maximum Marks: 100
PART – I
I. Choose the correct answer. Answer all the questions. [14 × 1 = 14]
Question 1.
If {(a, 8),(6, b)} represents an identity function, then the value of a and b are respectively …………. .
(1) (8,6)
(2) (8,8)
(3) (6,8)
(4) (6,6)
Answer:
(1) (8,6)
![]()
Question 2.
If the H.C.F of 65 and 117 is expressible in the form of 65m -117, then the value of m is …………. .
(1) 4
(2) 2
(3) 1
(4) 3
Answer:
(2) 2
Question 3.
In an A.P, the first term is 1 and the common difference is 4. How many terms of the A.P must be taken for their sum to be equal to 120?
(1) 6
(2) 7
(3) 8
(4) 9
Answer:
(3) 8
Question 4.
\(\frac{3 y-3}{y} \div \frac{7 y-7}{3 y^{2}}\) is …………. .
(1) \(\frac{9 y}{7}\)
(2) \(\frac{9 y^{3}}{(21 y-21)}\)
(3) \(\frac{21 y^{2}-42 y+21}{3 y^{3}}\)
(4) \(\frac{7\left(y^{2}-2 y+1\right)}{y^{2}}\)
Answer:
(1) \(\frac{9 y}{7}\)
Question 5.
If the roots of the equation q2x2 + p2x + r2 = 0 are the squares of the roots of the equation qx2 + px + r = 0, then q, p, r are in …………. .
(1) A.P
(2) G.P
(3) Both A.P and G.P
(4) none of these
Answer:
(2) G.P
![]()
Question 6.
The two tangents from an external points P to a circle with centre at O are PA and PB. If ∠APB = 70° then the value of ∠AOB is …………. .
(1) 100°
(2) 110°
(3) 120°
(4) 130°
Answer:
(2) 110°
Question 7.
A straight line has equation 8y = 4x + 21. Which of the following is true …………. .
(1) The slope is 0.5 and they intercept is 2.6
(2) The slope is 5 and the y intercept is 1.6
(3) The slope is 0.5 and the y intercept is 1.6
(4) The slope is 5 and they intercept is 2.6
Answer:
(1) The slope is 0.5 and they intercept is 2.6
Question 8.
A tower is 60 m height. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30° , then x is equal to …………. .
(1) 41.92 m
(2) 43.92 m
(3) 43 m
(4) 45.6 m
Answer:
(2) 43.92 m
Question 9.
A frustum of a right circular cone is of height 16 cm with radii of its ends as 8 cm and 20 cm. Then, the volume of the frustum is …………. .
(1) 3328π cm3
(2) 3228π cm3
(3) 3240π cm3
(4) 3340π cm3
Answer:
(1) 3328π cm3
![]()
Question 10.
If the standard deviation of x, y,zisp then the standard deviation of 3x + 5, 3y + 5, 3z + 5 is …………. .
(1) 3p + 5
(2) 3p
(3) p + 5
(4) 9p + 5
Answer:
(2) 3p
Question 11.
A purse contains 10 notes of ₹2,000, 15 notes of ₹500, and 25 notes of ₹200. One note is drawn at random. What is the probability that the note is either a ₹500 note or ₹200 note?
(1) \(\frac{1}{5}\)
(2) \(\frac{3}{10}\)
(3) \(\frac{2}{3}\)
(4) \(\frac{4}{5}\)
Answer:
(4) \(\frac{4}{5}\)
Question 12.
If f = {(6, 3) (8, 9) (5, 3) (-1, 6)} then the pre-images of 3 are …………. .
(1) 5 and -1
(2) 6 and 8
(3) 8 and -1
(4) 6 and 5
Answer:
(4) 6 and 5
Question 13.
If α and β are the roots of the equation x2 + 2x + 8 = 0 then the value of \(\frac{\alpha}{\beta}+\frac{\beta}{\alpha}\) is …………. .
(1) \(\frac{1}{2}\)
(2) 6
(3) \(\frac{3}{2}\)
(4) \(\frac{-3}{2}\)
Answer:
(4) \(\frac{-3}{2}\)
Question 14.
If x – y = 3 and x + 2y = 6 are the diameters of a circle then the centre is at the point …………. .
(1) (0,0)
(2) (1,2)
(3) (4, 1)
(4) (1,-1)
Answer:
(3) (4, 1)
![]()
PART-II
II. Answer any ten questions. Question No. 28 is compulsory. [10 × 2 = 20]
Question 15.
Let X = {3, 4, 6, 8}. Determine whether the relation
R = {(x, f(x)) |x ∈ X, f(x) = x2 + 1} is a function from X to N?
Answer:
f(x) = x2 + 1
f(3) = 32 + 1 = 9 + 1 = 10
f(4) = 42 + 1 = 16 + 1 = 17
f(6) = 62 + 1 = 36 + 1 = 37
f(8) = 82 + 1 = 64 + 1 = 65
ves. R is a function from X to N.
Question 16.
Find k if fof f(k) = 5 where f(k) = 2k – 1.
Answer:
fof(k) = f(f(k))
= 2(2k – 1) – 1 = 4k – 3
Thus, fof(k) = 4k – 3
But, it is given that fof (k) = 5
Therefore 4k – 3 = 5 ⇒ k = 2.
Question 17.
Find the least positive value of x such that 98 = (x + 4) mod 5
Answer:
98 ≡ (x + 4) (mod 5)
98 – (x + 4) = 5n , for some integer n.
94 – x = 5n
94 – x is a multiple of 5.
Therefore, the least positive value of x must be 4
Since 94 – 4 = 90 is the nearest multiple of 5 less than 94.
Question 18.
If the first term of an infinite G.P. is 8 and its sum to infinity is \(\frac { 32 }{ 3 }\) then find the common ratio.
Answer:
Here a = 8, S∞ = \(\frac{32}{3}\)
\(\frac{a}{1-r}=\frac{32}{3}\)
\(\frac{8}{1-r}=\frac{32}{3}\)
32 – 32r = 24 ⇒ 32 r = 8
r = \(\frac{8}{32}=\frac{1}{4}\)
Common ratio = \(\frac{1}{4}\)
![]()
Question 19.
Find the excluded values, of the expression \(\frac{x^{3}-27}{x^{3}+x^{2}-6 x}\)
Answer:
x3 – 27 = x3 – 33
= (x – 3) (x2 + x + 3)
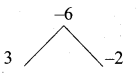
x3 + x2 – 6x = x(x2 + x – 6) = x (x + 3) (x – 2)
\(\frac{x^{3}-27}{x^{3}+x^{2}-6}=\frac{(x-3)\left(x^{2}+x+3\right)}{x(x+3)(x-2)}\)
The expression \(\frac{(x-3)\left(x^{2}+x+3\right)}{x(x+3)(x-2)}\) is undefined
when x (x + 3) (x – 2) = 0
x = 0 or x + 3 = 0 or x – 2 = 0
x = 0 or x = -3 or x = 2
The excluded values are 0, -3 and 2
Question 20.
Find the square root of \(1+\frac{1}{x^{6}}+\frac{2}{x^{3}}\)
Answer:
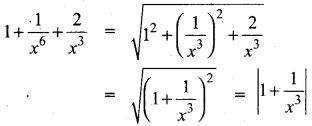
![]()
Question 21.
Find x and y if \(x\left[ \begin{matrix} 4 \\ -3 \end{matrix} \right] +\quad y\left[ \begin{matrix} -2 \\ 3 \end{matrix} \right] =\left[ \begin{matrix} 4 \\ 6 \end{matrix} \right] \)
Answer:
\(x\left[ \begin{matrix} 4 \\ -3 \end{matrix} \right] +y\left[ \begin{matrix} -2 \\ 3 \end{matrix} \right] =\left[ \begin{matrix} 4 \\ 6 \end{matrix} \right] \)
\(\left[ \begin{matrix} 4x \\ -3x \end{matrix} \right] +\left[ \begin{matrix} -2y \\ 3y \end{matrix} \right] =\left[ \begin{matrix} 4 \\ 6 \end{matrix} \right] \)
4x – 2y = 4
(1) ⇒ 2x – y = 2
(2) ⇒ -3x + 3y = 6
-x + y = 2
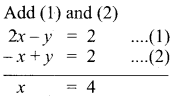
Substitute the Value of x = 4 in (2)
-4 + y = 2
y = 2 + 4 = 6
The value of x = 4 and y = 6
Question 22.
Show that in a triangle, the medians are concurrent.
Answer:
Medians are line segments joining each vertex to the midpoint of the corresponding opposite sides. Thus medians are the cevians where D, E, F are midpoints of BC, CA and AB respectively.
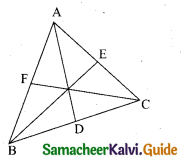
Since D is a midpoint of BC, BD = DC so \(\frac{B D}{D C}\) = 1 ….. (1)
Since, E is a midpoint of CA, CE = EA so \(\frac{C E}{E A}\) = 1 ……. (2)
Since, F is a midpoint of AB, AF = FB so \(\frac{A F}{F B}\) = 1 ……. (3)
Thus, multiplying (1), (2) and (3) we get,
\(\frac{\mathrm{BD}}{\mathrm{DC}} \times \frac{\mathrm{CE}}{\mathrm{EA}} \times \frac{\mathrm{AF}}{\mathrm{FB}}\) = 1 × 1 × 1 = 1
And so, Ceva’s theorem is satisfied. Hence the Medians are concurrent.
![]()
Question 23.
A cat is located at the point(-6, -4) in xy plane. A bottle of milk is kept at (5, 11). The cat wish to consume the milk travelling through shortest possible distance. Find the equation of the path it needs to take its milk.
Answer:
Equation of the joining the point is
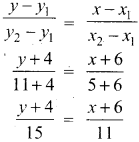
15(x + 6) = 11(y + 4)
15x + 90 = 11y + 44
15x – 11y + 90 – 44 = 0
15x – 11y + 46 = 0
The equation of the path is 15x – 11y + 46 = 0
Question 24.
If the circumference of a conical wooden piece is 484 cm then find its volume when its height is 105 cm.
Answer:
Circumference of the wooden piece = 484 cm
2πr = 484
2 × \(\frac { 22 }{ 7 }\) × r = 484 cm
r = \(\frac{484 \times 7}{2 \times 22}\)
r = 77 cm
Height of the wooden piece (h) = 105 cm
Volume of the conical wooden piect = \(\frac { 1 }{ 3 }\)πr2h cu. units
= \(\frac{1}{3} \times \frac{22}{7}\) × 77 × 77 × 105 cm3
= 22 × 11 × 77 × 35 cm3 = 652190 cm3
Volume of the wooden piece = 652190 cm3
Question 25.
The range of a set of data is 13.67 and the largest value is 70.08. Find the smallest value.
Answer:
Range R = 13.67
Largest value L = 70.08
Range R = L – S
13.67 = 70.08 – S
S = 70.08 – 13.67 = 56.41
Therefore, the smallest value is 56.41.
Question 26.
Three rotten eggs are mixed with 12 good ones. One egg is chosen at random. What is the probability of choosing a rotten egg?
Answer:
Number of good eggs = 12
Number of rotton eggs = 3
Totalnumberofeggs = 12 + 3 = 15
Sample space n (S) = 15
Let A be the event of choosirg a rotten egg
n(A) = 3
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{3}{15}=\frac{1}{5}\)
The Probability is \(\frac{1}{5}\)
![]()
Question 27.
Form the quadratic equation whose roots are 3 + √7 ; 3 – √7
Answer:
Sum of the roots = 3 + √7 + 3 – √7
= 6
Product of the roots (3 + √7) (3 – √7 )
= 32 – (√7)2
= 9 – 7
= 2
The required equation is x2 (sum of the roots) x + product of the roots = 0
x2 – (6)x + 2 = 0
x2 – 6x + 2 = 0
Question 28.
If a cos θ – b sin θ = c, then prove that (a sin θ + b cos θ) = ±\(\sqrt{a^{2}+b^{2}-c^{2}}\)
Answer:
Given a cos θ – bsin θ = c
Squaring on both sides
(a cos θ – b sin θ)2 = c2
a2cos2θ + b2sin2θ – 2 ab cosθ sinθ = c2
a2 (1 – sin2θ) + b2(1 – cos2θ) – 2ab cos θ sin θ = c2
a2 – a2 sin2 θ + b2 – b2cos2 θ – 2ab cos θ sin θ = c2
– a2 sin 2 θ – b2 cos2 θ – 2ab cos θ sin θ = – a2 – b2 + c2
a2 sin 2 θ + b2 cos2 θ + 2ab cos θ sin θ = + a2 + b2 – c2
(a sin θ + b cos θ)2 = a2 + b2 – c2
a sin θ + b cos θ = ± \(\sqrt{a^{2}+b^{2}-c^{2}}\)
Hence it is proved.
PART – III
III. Answer any ten questions. Question No. 42 is compulsory. [10 × 5 = 50]
Question 29.
A function f is defined by f(x) = 2x – 3
(i) find \(\frac{f(0)+f(1)}{2}\)
(ii) find x such that f(x) = 0.
(iii) find x such that f(x) = x.
(iv) find x such that f(x) = f( 1 – x).
Question 30.
If f(x) = 2x + 3, g(x) = 1 – 2x and h(x) = 3x. Prove that fo(goh) = (fog)oh
![]()
Question 31.
If S1, S2, S3, ,…S3m are the sums of n terms of m A.P.,s whose first terms are 1,2, 3, ……… m and whose common differences are 1, 3, 5 ,………. (2m – 1) respectively, then show that (S1 + S2 + S3 + ………. + Sm) = \(\frac { 1 }{ 2 }\)mn(mn + 1)
Question 32.
In an A.P., sum of four consecutive terms is 28 and their sum of their squares is 276. Find the four numbers.
Question 33.
Simplify \(\frac{12 t^{2}-22 t+8}{3 t} \div \frac{3 t^{2}+2 t-8}{2 t^{2}+4 t}\)
Question 34.
The hypotenuse of a right triangle is 6 m more than twice of the shortest side. If the third side is 2 m less than the hypotenuse, find the sides of the triangle.
Question 35.
Find the equation of a straight line parallel to Y axis and passing through the point of intersection of the lines 4x + 5y = 13 and x – 8y + 9 = 0.
Question 36.
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively.
If the distance between the ships is 200 \(\left(\frac{\sqrt{3}+1}{\sqrt{3}}\right)\) meters, find the height of the lighthouse.
Question 37.
Nathan, an engineering student was asked to make a model shaped like a cylinder with two cones attached at its two ends. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of the model that Nathan made.
Question 38.
The rainfall recorded in various places of five districts in a week are given below.

Find its standard deviation.
Question 39.
A bag contains 5 white and some black balls. If the probability of drawing a black ball from the bag is twice the probability of drawing a white ball then find the number of black balls.
Question 40.
If A = \(\left( \begin{matrix} 3 & 2 & 0 \\ 1 & 4 & 0 \\ 0 & 0 & 5 \end{matrix} \right) \) show that A2 – 7A + 10 I3
![]()
Question 41.
Find the values of “a” and “b” given that p(x) = (x2 + 3x + 2) (x2 – 4x + a) g(x) = (x2 – 6x + 9) (x2+ 4x + b) and their G.C.D. is (x + 2) (x – 3)
Question 42.
A container, open from the top made up of a metal sheet is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container at the rate of ₹ 40 per litre and the cost of metal sheet used if the costs ₹ 5 per 100 cm2, (use π = 3.14)
PART – IV
IV. Answer all the questions. [2 × 8 = 16]
Question 43.
(a) Draw a tangent to the circle from the point P having radius 3.6 cm, and centre at O. Point P is at a distance 7.2 cm from the centre.
[OR]
(b) Construct a ∆PQR such that QR = 6.5 cm, ∠P = 60° and the altitude from P to QR is of length 4.5 cm.
![]()
Question 44.
(a) Draw a graph of y = 2x2 + x – 6 and hence solve the 2x2 + x – 10 = 0.
[OR]
(b) Draw the graph of y = x2 – 5x + 6 and hence solve x2 – 5x + 6 = 0.