Students can download Maths Chapter 8 Statistics and Probability Ex 8.5 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 8 Statistics and Probability Ex 8.5
Multiple Choice Questions.
Question 1.
Which of the following is not a measure of dispersion?
(1) Range
(2) Standard deviation
(3) Arithmetic mean
(4) Variance
Answer:
(3) Arithmetic mean
Hint:
Measures of dispersion are,
(i) Range
(ii) Mean deviation
(iii) Quartile deviation
(iv) Standard deviation
(v) Variance
(vi) coefficient of variation
Question 2.
The range of the data 8, 8, 8, 8, 8.. . 8 is
(1) 0
(2) 1
(3) 8
(4) 3
Solution:
(1) 0
Hint
R = L – S = 8 – 8 = 0
![]()
Question 3.
The sum of all deviations of the data from its mean is _______
(1) always positive
(2) always negative
(3) zero
(4) non-zero integer
Answer:
(3) zero
Question 4.
The mean of 100 observations is 40 and their standard deviation is 3. The sum of squares of all deviations is
(1) 40000
(2) 160900
(3) 160000
(4) 30000
Solution:
(2) 160900
Hint:
σ = 3
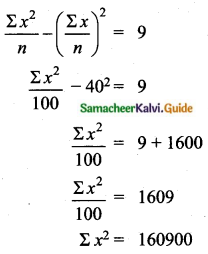
Question 5.
Variance of first 20 natural numbers is ______
(1) 32.25
(2) 44.25
(3) 33.25
(4) 30
Answer:
(3) 33.25
Hint:
Variance of 20 natural numbers is
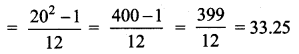
Question 6.
The standard deviation of a data Is 3. If each value is multiplied by 5 then the new variance is
(1) 3
(2) 15
(3) 5
(4) 225
Solution:
σ = 3. 1f each is multiplied by 5. The new standard variation is also multiplied by 3.
∴ The new S.D = 5 × 3 = 15
Variance = 152 = 225
![]()
Question 7.
If the standard deviation of x, y, z is p then the standard deviation of 3x + 5, 3y + 5, 3z + 5 is ________
(1) 3p + 5
(2) 3p
(3) p + 5
(4) 9p + 15
Answer:
(2) 3p
Hint:
(i) Each value is added by any constant there is no change in standard deviation.
(ii) Each value is multiplied by 3 standard deviations also multiplied by 3.
The standard deviation is 3p.
Question 8.
If the mean and coefficient of variation of a data are 4 and 87.5% then the standard
deviation is
(1) 3.5
(2) 3
(3) 4.5
(4) 2.5
Solution:
(1) 3.5
Hint:
\(\bar{x}\) = 4, coefficient of variation is = 87. 5%
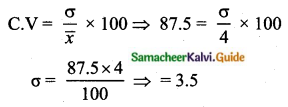
Question 9.
Which of the following is incorrect?
(1) P(A) > 1
(2) 0 ≤ P(A) ≤ 1
(3) P(Φ) = 0
(4) P(A) + P(\(\bar{A}\)) = 1
Answer:
(1) P(A) > 1
Hint:
Probability is always less than one or equal to one.
![]()
Question 10.
The probability a red marble selected at random from a jar containing p red, q blue and r green marbles is _________
(1) \(\frac{q}{p+q+r}\)
(2) \(\frac{p}{p+q+r}\)
(3) \(\frac{p+q}{p+q+r}\)
(4) \(\frac{p+r}{p+q+r}\)
Answer:
(1) \(\frac{q}{p+q+r}\)
Hint:
Sample spaces = p + q + r
Let A be the event of getting red
n(A) = p
P(A) = \(\frac{q}{p+q+r}\)
Question 11.
A page is selected at random from a book. The probability that the digit at units place of the page number chosen is less than 7 is _______
(1) \(\frac{3}{10}\)
(2) \(\frac{7}{10}\)
(3) \(\frac{3}{9}\)
(4) \(\frac{7}{9}\)
Answer:
(2) \(\frac{7}{10}\)
Hint:
Here n(S)= 10 (given digit at imit place. It has two digit)
n(A) = 7
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{7}{10}\)
![]()
Question 12.
The probability of getting a job for a person is \(\frac{x}{3}\). If the probability of not getting the job is \(\frac{2}{3}\) then the value of x is.
(1) 2
(2) 1
(3) 3
(4) 1.5
Solution:
(2) 1
Hint:
Probability of getting a job = \(\frac{x}{3}\)
Probability of not getting a job = 1 – \(\frac{x}{3}\)
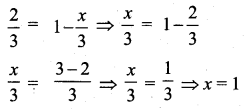
Question 13.
Kamalam went to play a lucky draw contest. 135 tickets of the lucky draw were sold. If the probability of Kamalam winning is \(\frac{1}{9}\), then the number of tickets bought by Kamalam is _______
(1) 5
(2) 10
(3) 15
(4) 20
Answer:
(3) 15
Hint:
n(S) = 135
P(A) = \(\frac{1}{9}\)
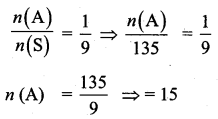
Question 14.
If a letter is chosen at random from the English alphabets {a, b, …, z}, then the probability that the letter chosen precedes x.
(1) \(\frac{12}{13}\)
(2) \(\frac{1}{13}\)
(3) \(\frac{23}{26}\)
(4) \(\frac{3}{26}\)
Solution:
(3) \(\frac{23}{26}\)
Hint:
n(S) = 26
Let A denote the letter chosen precedes x
A= {a, b, c, d, …, x}
n(A) = 23
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{23}{26}\)
![]()
Question 15.
A purse contains 10 notes of ₹ 2000, 15 notes of ₹ 500, and 25 notes of ₹ 200. One note is drawn at random. What is the probability that the note is either a ₹ 500 note or ₹ 200 note?
(1) \(\frac{1}{5}\)
(2) \(\frac{3}{10}\)
(3) \(\frac{2}{3}\)
(4) \(\frac{4}{5}\)
Answer:
(4) \(\frac{4}{5}\)
Hint:
Sample space (S) = 10 + 15 + 25 = 50
n(S) = 50
Let A be the event of getting ₹ 500 note
n (A) = 15
P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{15}{50}\)
Let B be the event of getting ₹ 200 note
n (B) = 25
P(B) = \(\frac{n(\mathrm{B})}{n(\mathrm{S})}=\frac{25}{50}\)
Probability of the note is either a ₹ 500 note or ₹ 200 note
P(A) + P(B) = \(\frac{15}{50}+\frac{25}{50}\) = \(\frac{40}{50}\) = \(\frac{4}{5}\)