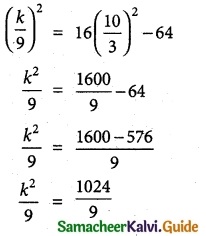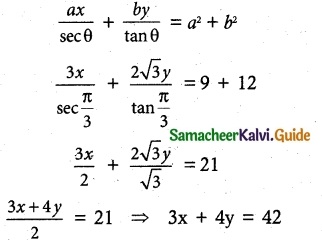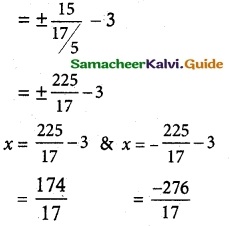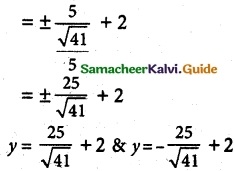Bhagya

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.5 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.5

Question 1.
A bridge has a parabolic arch that is 10 m high in the centre and 30 m wide at the bottom. Find the height of the arch 6 m from the centre, on either sides.
Solution:

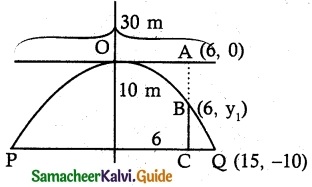
PQ = 2a = 30 m
a = 15 m
Point Q be (15 , -10)
Equation of the parabola
x² = -4 ay …….. (1)
Q lies on parabola
15² = -4a( -10)
a = \(\frac {225}{40}\)
(1) ⇒ x² = -4(\(\frac {225}{40}\))y
x² = \(\frac {225}{10}\)y
Let B(6, y) lies on parabola
6² = \(\frac {225}{10}\) y₁
y₁ = –\(\frac {36×10}{225}\) = \(\frac {-8}{5}\) = \(\frac {8}{5}\) m
AB = AC – BC = 10 – \(\frac {8}{5}\)
= \(\frac {50-8}{5}\) = \(\frac {42}{5}\)
AB = 8.4 m
∴ The height of the arch 6 m from the centre is 8.4 m.

Question 2.
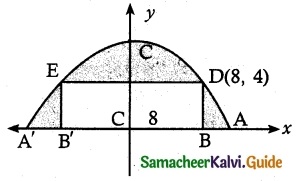
A tunnel through a mountain for a four lane highway is to have a elliptical opening. The total width of the highway (not the opening) is to be 16 m and the height at the edge of the road must be sufficient for a truck 4 m high to clear if the highest point of the opening is to be 5 m approximately. How wide must the opening be?
Solution:

Let the equation of the ellipse be
\(\frac {x^2}{a^2}\) + \(\frac {y^2}{b^2}\) = 1
Length of semi minor axis b = 5
i,e., \(\frac {x^2}{a^2}\) + \(\frac {y^2}{5^2}\) = 1
Let BB’ be the road width and AA’ be the end points of the opening of the tunnel.
Let CB = 8, BD = 4
∴ D is (8, 4) lies on the ellipse
\(\frac {8^2}{a^2}\) + \(\frac {4^2}{5^2}\) = 1
⇒ a² = \(\frac {25}{9}\) × 64
⇒ a = \(\frac {40}{3}\)
The width AA’ = 2a
= \(\frac {80}{3}\) = 26.66 m
The required width is 26.66 m.

Question 3.
At a water fountain, water attains a maximum height of 4 m at horizontal distance of 0.5 m from its origin. If the path of water is a parabola, find the height of water at a horizontal distance of 0.75 m from the point of origin.
Solution:

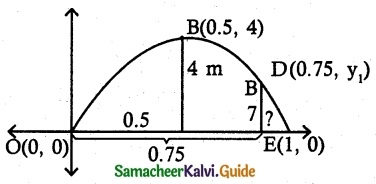
Let the equation of parabola be
(x – h)² = -4a (y – k)
Here vertex B (0.5, 4)
∴ Equation of parabola
(x – 0.5)² = -4a(y – 4)
Parabola passes through origin (0, 0)
(0 – 0.5)² = -4a(0 – 4)
(-\(\frac {1}{2}\))² = 16a
∴ \(\frac {1}{4}\) = 16a ⇒ a = \(\frac {1}{64}\)
∴ Equation of parabola
(x – 0.5)² = -4(\(\frac {1}{64}\))(y- 4)
This Parabola passes again through D(0.75, y₁)
∴ (0.75 – 0.5)² = –\(\frac {1}{16}\) (y₁ – 4)
(0.25)² = –\(\frac {1}{16}\) (y₁ – 4)
(\(\frac {1}{4}\))² = –\(\frac {1}{16}\) (y₁ – 4)
\(\frac {1}{16}\) = –\(\frac {1}{16}\) (y₁ – 4)
1 = -y₁ + 4
y₁ = 3
Height of water at a horizontal distance of 0.75 m is 3 m.

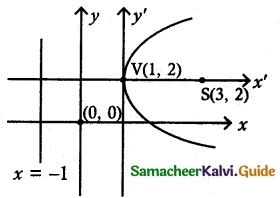
Question 4.
An engineer designs a satellite dish with a parabolic cross section. The dish is 5 m wide at the opening and the focus is placed 1.2 m from the vertex
(a) Position a co-ordinate system with the origin at the vertex and the x-axis on the parabola’s axis of symmetry and find an equation of the parabola.
(b) Find the depth of the satellite dish at the vertex.
Solution:

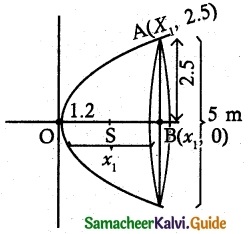
(a) Consider the satellite dish is open rightward parabola
y² = 4 ax ……….. (1)
Clearly a = 1.2m
(1) ⇒ y² = 4(1.2)
y² = 4.8x
(b) Use the point (x₁, 2.5) in (1)
(2.5)² = 4(1.2)x₁
\(\frac{(2.5)^{2}}{4(1.2)}\) = y₁
x₁ = 1.3 m
∴ The depth of the satellite dish at vertex is 1.3 m

Question 5.
The parabolic cable of a 60 m portion of the roadbed of a suspension bridge are positioned as shown below. Vertical cables are to be spaced every 6 m along this portion of the roadbed. Calculate; the lengths of first two of these vertical cables: from the vertex.

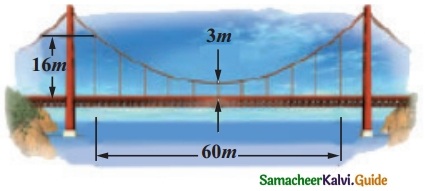
Solution:

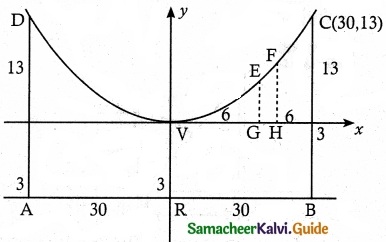
From the diagram, the equation is x² = 4 ay and it passes through C(30, 13)
Equation of Parabola x² = 4ay.
30² = 4a × 13
4a = \(\frac {30^2}{13}\)
∴ Equation of the parabola is
x² = \(\frac {30^2}{13}\)y
(i) Let VG = 6 and GE = y
∴ E is (6, y) and it lies on the parabola
36 = \(\frac {30^2}{13}\)y
⇒ y = 0.52
Gable from the road = 3 + 0.52
= 3.52 m.

(ii) Let VH = 12 and HF = y
∴ F (12, y) lies on the parabola
12² = \(\frac {30^2}{13}\)y
⇒ y = \(\frac {144×13}{900}\)
= \(\frac {208}{100}\)y
y = 2.08
Cable from the road = 3 + 2.08 = 5.08
The heights of the first two vertical cables from the vertex are 3.52 m and 5.08 m

Question 6.
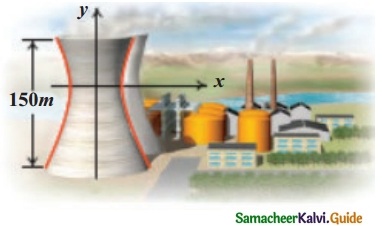
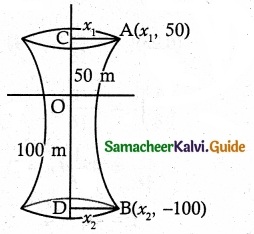
Cross-section of a Nuclear cooling tower is in the shape of a hyperbola with equation \(\frac {x^2}{30^2}\) – \(\frac {y^2}{44^2}\) = 1. The tower is 150 m tall and the distance from the top of the tower to the centre of the hyperbola is half the distance from the base of the tower to the centre of the hyperbola. Find the diameter of the top and base of the tower.

Solution:

Equation of hyperbola is \(\frac {x^2}{30^2}\) – \(\frac {y^2}{44^2}\) = 1
Given OC = \(\frac {1}{2}\) OD and CD = 150
∴ OC = 50 m and OD = 100 m
Let the Radius of top of the tower be x₁ and bottom of the tower be x₂.
∴ Points A(x₁, 50) and B(x₂, 100)
Hyperbola passes through A(x₁, 50)

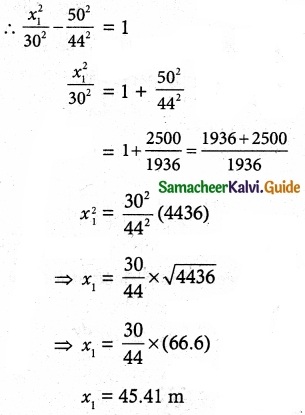
∴ Radius of the top = 45.41 m.
Diameter of the top = 90.82 m
Also
The hyperbola again passes through B(x₂, 100)

∴ Radius of the base = 74.48 m.
Diameter of the base = 148.96 m
∴ Diameter of the top and base of the tower are 90.82 m and 148.96 m.

Question 7.
A rod of length 1.2 m moves with its ends always touching the co-ordinate axes. The locus of a point P on the rod, which is
0. 3 m from the end in contact with x axis is an ellipse. Find the eccentricity.
Solution:

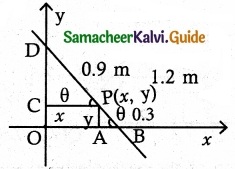
Length of rod BD = 1.2 m
Let P(x, y) be any point on the Rod such
that PB = 0.3 m
∴ PD = 1.2 – 0.3 = 0.9 m
Let ΔPAB and ΔPCD are similar triangles
In ΔPAB sin θ = \(\frac {y}{0.3}\)
In A PCB cos θ = \(\frac {y}{0.9}\)
We know that sin² θ + cos² θ = 1

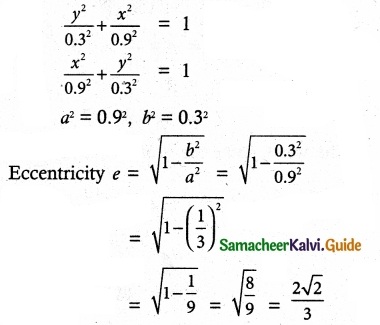
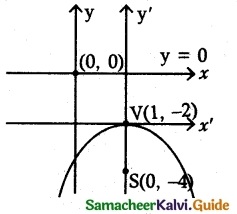
Question 8.
Assume that water’issuing from the end of a horizontal pipe, 7.5 m. above the ground, describes a parabolic path. The vertex of the parabolic path is at The end of the pipe. At position 2.5 in below the line of the pipe, the flow of water has curved outward 3 m beyond the vertical, line through the end of the pipe. How far beyond this vertical line will the water strike the ground?
Solution:

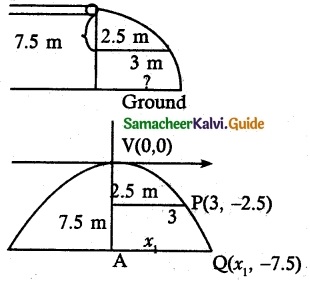
Equation of the water path is
x² = – 4 ay
Use the point (3, – 2.5) in (1)
(3)² = – 4a(- 2.5)
9 = 10a
a = \(\frac{9}{10}\) substituting in (1)
(1) ⇒ x² = -4\(\frac{9}{10}\)y …………. (2)
Use the point (x₁, -7.5) in (2)
(2) ⇒ x₁² = -4 \(\frac{9}{10}\)(-7.5) ⇒ x₁² = 30(\(\frac{9}{10}\))
x₁ = \(\sqrt{3 \times 9}\)
x₁ = \(3 \sqrt{3}\) m
∴ The water strikes the ground \(3 \sqrt{3}\) m beyond the vertical line.

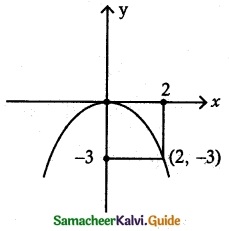
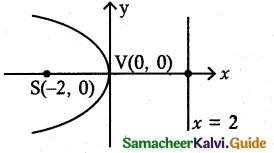
Question 9.
On lighting a rocket cracker it gets projected in a parabolic path and reaches a maximum height of 4 in when it is 6 m away from the point of projection. Finally, it reaches the ground 12 in away from the starting-point. Find the angle of! projection.
Solution:

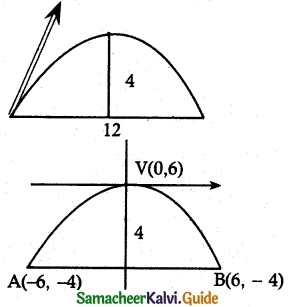
Equation of the parabola be x² = – 4ay ……. (1)
B(6, -4) lies on parabola
6² = -4a(-4)
\(\frac {36}{16}\) = a ⇒ a = \(\frac {9}{4}\)
(1) ⇒ x² = -(\(\frac {9}{4}\))y
x² = -9y ………. (2)
Now need tofind slope at (-6, -4)
Diff (2) w.r.to x
2x = -9 \(\frac {dy}{dx}\)
\(\frac {dy}{dx}\) = \(\frac {2x}{-9}\)
At(-6, -4), \(\frac {dy}{dx}\) = \(\frac {2(-6)}{-9}\) = \(\frac {12}{9}\) = \(\frac {4}{3}\)
tan θ = \(\frac {4}{3}\)
θ = tan^-1(\(\frac {4}{3}\))

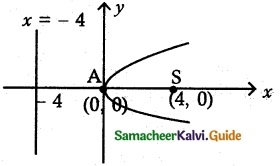
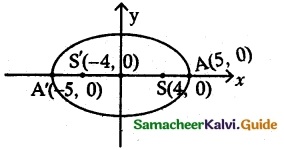
Question 10.
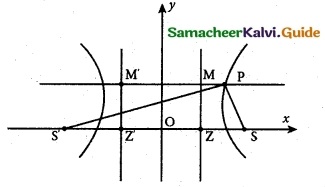
Points A and B are 10 km apart and it is determined from the sound of an explosion heard at those points at different times that the location of the explosion is 6 km closer to A than 5. Show that the location of the explosion is restricted to a particular curve and find an equation of it.
Solution:
As shown in figure, A and B are on both sides of x-axis at Co-ordinates (-5, 0) and (5, 0)
The distance between A and B is 10. A point C is on the graph at Co-ordinates (x, y)
C is 6 km closer to A than B.

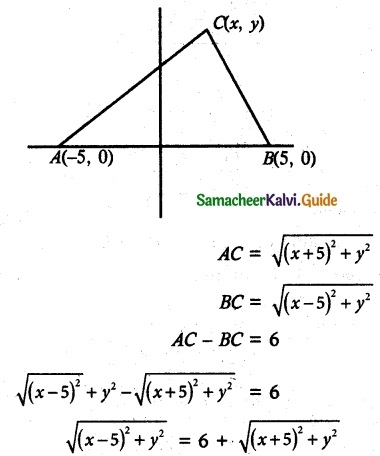
Squaring on both sides we get,
(x – 5)² + y² = 36 + (x + 5)² + y² + 12(\(\sqrt {(x+5)^2+y^2}\))
x² + 25 – 10x + y² = x² + 10x + y² + 36 + 25 + 12\(\sqrt {(x+5)^2+y^2}\)
-20x – 36 = 12\(\sqrt {(x+5)^2+y^2}\)
(÷ by 4) ⇒ -5x – 9 = 3\(\sqrt {(x+5)^2+y^2}\)
Squaring both sides we get,
25x² + 81 + 90x = 9(x² + 25 + 10x + y²)
25x² + 81 + 90x – 9x² – 90x – 9y² – 225 = 0
16x² – 9y² – 144 = 0
16x² – 9y² = 144
(÷ by 144) ⇒ \(\frac {x^2}{9}\) – \(\frac {y^2}{16}\) = 1 is the required equation of hyperbola.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.4 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.4

Question 1.
Find the equations of the two tangents that can be drawn from (5, 2) to the ellipse 2x² + 7y² = 14.
Solution:
2x² + 7y² = 14
(÷ by 14) ⇒ \(\frac{x^{2}}{7}+\frac{y^{2}}{2}\) = 1
comparing this equation with \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
we get a² = 7 and b² = 2
The equation of tangent to the above ellipse will be of the form
y = mx + \(\sqrt{a^{2} m^{2}+b^{2}}\) ⇒ y = mx + \(\sqrt{7 m^{2}+2}\)
Here the tangents are drawn from the point (5, 2)
⇒ 2 = 5m + \(\sqrt{7 m^{2}+2}\) ⇒ 2 – 5m = \(\sqrt{7 m^{2}+2}\)
Squaring on both sides we get
(2 – 5m)² = 7m² + 2
25m² + 4 – 20m – 7m² – 2 = 0
18m² – 20m + 2 = 0
(÷ by 2) ⇒ 9m² – 10m + 1 = 0
(9m – 1) (m – 1) = 0
‘ m = 1 (or) m = 1/9
When m = 1, the equation of tangent is
y = x + 3 or x – y + 3 = 0
When m = \(\frac{1}{9}\) the equation of tangent is 9
y = \(=\frac{x}{9}+\sqrt{\frac{7}{81}+2}\) (i.e.) y = \(\frac{x}{9}+\frac{13}{9}\)
9y = x + 13 or x – 9y + 13 = 0

Question 2.
Find the equations of tangents to the hyperbola \(\frac {x^2}{16}\) – \(\frac {y^2}{64}\) = 1 which are parallel to 10x – 3y + 9 = 0.
Solution:
Equation of Hyperbola \(\frac {x^2}{16}\) – \(\frac {y^2}{64}\) = 1
∴ a² = 16, b² = 64
Tangent is parallel to the line
10x – 3y + 9 = 0 is
10x – 3y + k = 0
∴ 3y = 10x + k
y = \(\frac {10}{3}\)x + \(\frac {k}{3}\)
∴ m = \(\frac {10}{3}\) c = \(\frac {k}{3}\)
Condition that the line y = mx + c to be tangent to the hyperbola is
c² = a²m² – b²

k² = 1024
k = ±32
∴ Equation of tangent
⇒ 10x – 3y ± 32 = 0

Question 3.
Show that the line x – y + 4 = 0 is a tangent to the ellipse x² + 3y² = 12. Also find the co-ordinates of the point of contact.
Solution:
The given ellipse is x² + 3y² = 12
(÷ by 12) ⇒ \(\frac{x^{2}}{12}+\frac{y^{2}}{4}\) = 1
(ie.,) Here a² = 12 and b² = 4
The given line is x – y + 4 = 0
(ie.,) y = x + 4
Comparing this line with y = mx + c
We get m = 1 and c = 4
The condition for the line y = mx + c
To be a tangent to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 is c² = a²m² + b²
LHS = c² = 4² = 16
RHS: a²m² + b² = 12( 1 )² + 4 = 16
LHS = RHS The given line is a tangent to the ellipse. Also the point of contact is
\(\left(\frac{-a^{2} m}{c}, \frac{b^{2}}{c}\right)=\left[-\left(\frac{12(1)}{4}\right), \frac{4}{4}\right]\) (i.e.,) (-3, 1)

Question 4.
Find the equation of the tangent to the parabola y² = 16x perpendicular to 2x + 2y + 3 = 0.
Solution:
Equation of the parabola
y² = 16x
4 a = 16
a = 4
Tangent is perpendicular to the line
2x + 2y + 3 = 0 is 2x – 2y + k = 0
2x – 2y + k = 0
2y = 2x + k
y = x + \(\frac {k}{2}\)
m = 1 c = \(\frac {k}{2}\)
Condition that the line y = mx + c to be tangent to the parabola is
c = \(\frac {a}{m}\)
\(\frac {k}{2}\) = \(\frac {4}{1}\)
k = 8
Equation of the tangent
2x – 2y + 8 = 0
÷ by 2 ⇒ x – y + 4 = 0

Question 5.
Find the equation of the tangent at t = 2 to the parabola y² = 8x (Hint: use parametric form).
Solution:
y² = 8x
Comparing this equation with y² = 4ax
we get 4a = 8 ⇒ a = 2
Now, the parametric form for y² = 4ax is x = at², y = 2at
Here a = 2 and t = 2
⇒ x = 2(2)² = 8 and y = 2(2) (2) = 8
So the point is (8, 8)
Now eqution of tangent to y² = 4 ax at (x₁, y₁) is yy₁ = 2a(x + x₁)
Here (x₁, y₁) = (8, 8) and a = 2
So equation of tangent is y(8) = 2(2) (x + 8)
(ie.,) 8y = 4 (x + 8)
(÷ by 4) ⇒ 2y = x + 8 ⇒ x – 2y + 8 = 0
Aliter
The equation of tangent to the parabola y² = 4ax at ‘t’ is
yt = x + at²
Here t = 2 and a = 2
So equation of tangent is
(i.e.,) y(2) = x + 2(2)²
2y = x + 8 ⇒ x – 2y + 8 = 0

Question 6.
Find the equations of the tangent and normal to hyperbola 12x² – 9y² = 108 at θ = \(\frac {π}{3}\) .
(Hint: use parametric form)
Solution:
(i) Equation of the tangent to hyperbola be

⇒ 4x – 3y = 6
⇒ 4x – 3y – 6 = 0

(ii) Equation of the normal to hyperbola be

⇒ 3x + 4y – 42 = 0

Question 7.
Prove that the point of intersection of the tangents at ‘t₁‘ and ‘t₂‘ on the parabola y² = 4ax is [at₁t₂, a(t₁ + t₂)].
Solution:
Equation of the tangent of parabola y² = 4ax be
at t₁ yt₁ = x + at₁² ……….. (1)
at t₂ yt₂ yt = x + at₂² ……….. (2)
(1) – (2) ⇒ y(t₁ – t₂) = a(t₁² – t₂²)
y(t₁ – t₂) = a(t₁ + t₂)(t₁ – t₂)
y = a(t₁ + t₂)
(1) ⇒ t₁a(t₁ + t₂) = x + at₁²
x = at₁² + at₁t₂ – at₁²
x = at₁t₂
Point of intersection be [at₁t₂, a(t₁ + t₂)]

Question 8.
If the normal at the point ‘t₁‘ on the parabola y² = 4ax meets the parabola again at the point t₂ then prove that t₂ = -(t₁ + \(\frac {2}{t_1}\))
Solution:
Equation of normal to y² = 4at’ t’ is y + xt = 2at + at³.
So equation of normal at ‘t₁’ is y + xt₁ = 2at₁ + at₁³
The normal meets the parabola y² = 4ax at ‘t₂’ (ie.,) at (at₂², 2at₂)
⇒ 2at₂ + at₁t₂² = 2at₁ + at₁³
So 2a(t₂ – t₁) = at₁³ – at₁t₂²
⇒ 2a(t₂ – t₁) = at₁(t₁² – t₂²)
⇒ 2(t₂ – t₁) = t₁(t₁ + t₂)(t₁ – t₂)
⇒ 2= -t₁(t₁ + t₂)
⇒ t₁ + t₂ = \(\frac{-2}{t_{1}}\)
⇒ t₂ = \(-t_{1}-\frac{2}{t_{1}}=-\left(t_{1}+\frac{2}{t_{1}}\right)\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.3 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.3

Question 1.
Identify the type of conic section of each of the equations.
(1) 2x² – y² = 7
(2) 3x² + 3y² – 4x + 3y + 10 = 0
(3) 3x² + 2y² = 14
(4) x² + y² + x – y = 0
(5) 11x² – 25y² – 44x + 50y – 256 = 0
(6) y² + 4x + 3y + 4 = 0
Solution:
(1) 2x² – y² = 7
Comparing this equation with the general equation of the conic
Ax² + Bxy + Cy² + Dx + Ey + F = 0
We get A = 2, C = – 1
Elere A ≠ C also A and C are of opposite signs.
So the conic is a hyperbola.

(2) 3x² + 3y² – 4x + 3y + 10 = 0
A = 3, B = 0, C = 3, D = -4, E = 3, F = 10
A = C and B = 0 (No xy term)
∴ It is a circle.

(3) 3x² + 2y² = 14
A = 3, B = 0, C = 2, F = -14
A ≠ C and A & C are the same signs.
∴ It is an ellipse.

(4) x² + y² + x – y = 0
Comparing this equation with the general equation of the conic
Ax² + Bxy + Cy² + Dx + Ey + F = 0
We get A = C and B = 0
So the given conic is a circle.

(5) 11x² – 25y² – 44x + 50y – 256 = 0
A =11, B = 0, C = -25, D = -44, E = 50, F = -256
A ≠ C and A & C are the opposite signs.
∴ It is a hyperbola.

(6) y² + 4x + 3y + 4 = 0
Comparing this equation with the general equation of the conic
Ax² + Bxy + Cy² + Dx + Ey + F = 0
We get A = 0 and B = 0
So the conic is a parabola.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.2 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.2

Question 1.
Find the equation of the parabola in each of the cases given below:
(i) focus (4, 0) and directrix x = -4.
(ii) passes through (2, – 3) and symmetric about y axis.
(iii) vertex (1,-2) and focus (4, – 2).
(iv) end points of latus rectum (4, -8) and (4, 8).
Solution:
(i) focus (4, 0) and directrix x = -4
Parabola is open rightwards vertex (0, 0)

a = 4
(Distance AS = 4 unit)
f² = 4(4) x
Equation of parabola
y² = 16x.

(ii) passes through (2, – 3) and symmetric about y-axis

x² = 4ay
It passes through (2, -3)
⇒ 2² = 4a(-3)
4 = -12a ⇒ a = \(-\frac{1}{3}\) ⇒ 4a = \(-\frac{4}{3}\)
∴ Equation of parabola is x² = \(-\frac{4}{3}\) y
3x²= – 4y.

(iii) vertex (1,-2) and focus (4, – 2)

In given data the parabola is open rightwards and symmetric about the line parallel to x-axis.
Equation of parabola
(y – k)² = 4a(x – h)
Vertex (h, k) = (1, -2)
(y + 2)² = 4a(x – 1)
a = AS = 3
Equation of parabola
(y + 2)² = 4(3)(x – 1)
(y + 2)² = 12(x – 1)

(iv) end points of latus rectum (4, -8) and (4, 8)

Focus = (4, 0)
Equation of the parabola will be of the form y² = 4ax
Here a = 4
⇒ y² = 16x

Question 2.
Find the equation of the ellipse in each of the cases given below:
(i) foci (± 3, 0), e = \(\frac {1}{2}\)
(ii) foci (0, ±4) and end points of major axis are (0, ±5).
(iii) length of latus rectum 8, eccentricity = \(\frac {3}{5}\) and major axis on x-axis.
(iv) length of latus rectum 4, distance between foci and major axis as y axis.
Solution:
(i) foci (± 3, 0), e = \(\frac {1}{2}\)
foci (± c, 0) = (± 3, 0)

e = \(\frac {1}{2}\)
c = ae = 3
a(\(\frac {1}{2}\)) = 3
a = 6 ⇒ a² = 36
b² = a² – c²
b² = 36 – 9 = 27
b² = 27
Equation of the ellipse be \(\frac {x^2}{a^2}\) + \(\frac {y^2}{b^2}\) = 1
\(\frac {x^2}{36}\) + \(\frac {y^2}{27}\) = 1

(ii) foci (0, ±4) and end points of major axis are (0, ±5)

foci (0, ±c) = (0, +4)
vertex (0, ±a) = (0, ±5)
∴ c = 4, a = 5
ae = 4
5e = 4
e = \(\frac {4}{5}\)
b² = a² – c²
= 25 – 16
b² = 9
Equation of the ellipse be \(\frac {x^2}{b^2}\) + \(\frac {y^2}{a^2}\) = 1
\(\frac {x^2}{9}\) + \(\frac {y^2}{25}\) = 1

(iii) length of latus rectum 8, eccentricity = \(\frac {3}{5}\) and major axis on x-axis.
e = \(\frac {3}{5}\)
Latus rectum \(\frac {2b^2}{a}\) = 8

(iv) length of latus rectum 4, distance between foci 4√2 and major axis as y-axis

Given \(\frac{2 b^{2}}{a}\) = 4 and 2ae = \(4 \sqrt{2}\)
Now \(\frac{2 b^{2}}{a}\) = 4 2b² = 4a
⇒ b² = 2a
2ae = \(4 \sqrt{2}\) ae = \(2 \sqrt{2}\)
So a²e² = 4(2) = 8
We know b² = a²(1 – e²) = a² – a²e²
⇒ 2a = a² – 8 ⇒ a² – 2a -8 = 0
⇒ (a – 4) (a +2) = 0 ⇒a = 4 or -2
As a cannot be negative
a = 4 So a² = 16 and b² = 2(4) = 8
Also major axis is along j-axis
So equation of ellipse is \(\frac{x^{2}}{8}+\frac{y^{2}}{16}\) = 1

Question 3.
Find the equation of the hyperbola in each of the cases given below:
(i) foci (± 2, 0), eccentricity = \(\frac {3}{2}\)
(ii) centre (2, 1) one of the foci (8, 1) and corresponding directrix x = 4.
(iii) passing through (5, -2) and length of the transverse axis along x axis and length 8 units.
Solution:
(i) foci (± 2, 0), eccentricity = \(\frac {3}{2}\)

(ii) centre (2, 1) one of the foci (8, 1) and corresponding directrix x = 4.
Distance CS = ae = 6 …….. (1)
Directrix \(\frac {a}{e}\) = 4 ……… (2)
(1) × (2) ⇒ ae × \(\frac {a}{e}\) = 24
a² = 24

∴ c = ae = 6
b² = c² – a²
= 36 – 24 = 12
The transverse axis is parallel to x-axis
∴ \(\frac {(x-h)^2}{a^2}\) – \(\frac {(y – k)^2}{b^2}\) = 1 (h, k) = (2, 1)
\(\frac {(x-2)^2}{24}\) – \(\frac {(y – 1)^2}{12}\) = 1

(iii) passing through (5,-2) and length of the transverse axis along x axis and of length 8 units.
Transverse axis along x-axis
\(\frac {x^2}{a^2}\) – \(\frac {y^2}{b^2}\) = 1
Length of transverse axis 2a = 8
⇒ a = 4

Question 4.
Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
(i) y² = 16x
(ii) x² = 24y
(iii) y² = -8x
(iv) x² – 2x + 8y + 17 = 0
(v) y² – 4y – 8x + 12 = 0
Solution:
(i) y² = 16x

4a = 16
a = 4
(a) Vertex V (0, 0)
(b) Focus S(a, 0) = S(4, 0)
(c) Equation of the directrix x = – a
x = -4 ⇒ x + 4 = 0
(d) Length of the latus rectum = 4a = 4(4)
= 16

(ii) x² = 24y

(a) Vertex V (0, 0),
(b) Focus S (0, a) = S(0, 6)
(c) Equation of the directrix y = -a = -6
⇒ y + 6 = 0
(d) Length of the latus rectum = 4a
= 4 (6) = 24

(iii) y² = -8x
4a = 8,
a = 2

(a) Vertex V(0, 0) = ( 0, 0)
(b) Focus S(-a, 0) = (-2, 0)
(c) Equation of the directrix x = a = 2
x – 2 = 0
(d) Length of the latus rectum 4a = 8
(iv) x² – 2x + 8y + 17 = 0
x² – 2x = -8y – 17
(x – 1)² = -8y – 17 + 1
(x – 1)² = -8y – 16
(x – 1)² = -8(y + 2)
It is form of (x – h)² = -4a(y – k)
4a = 8 ⇒ a = 2
(a) Vertex be (h, k) = (1, -2)

(b) Foeus = (0 +h, -a + k) = (0 + 1, -2 – 2) = (1, -4)
(c) Equation of the directrix is y + k + a = 0
y – 2 + 2= 0
y = 0
(d) Length of latus rectum is 4a = 4 × 2 = 8 units,

(v) y² – 4y – 8x + 12 = 0

y² – 4y = 8x – 12
(y – 2)² = 8x – 12 + 4
= 8x – 8
= 8 (x – 1)
(y – 2)² = 8 (x – 1)
It is form of (y – k)² = Aa(x – h)
4a = 8 ⇒ a = 2
(a) Vertex (h, k) = (1, 2)
(b) Focus = (a+h, 0 + k) = (2 + 1, 0 + 2) = (3, 2)
(c) Equation of the directrix x = -a + h
= -2 + 1
= -1
x + 1 = 0
(d) Length of latus rectum is
4a = 4 × 2 = 8 units.

Question 5.
Identify the type of conic and find centre, foci, vertices and directrices of each of the following:
(i) \(\frac {x^2}{25}\) + \(\frac {y^2}{9}\) = 1
(ii) \(\frac {x^2}{3}\) + \(\frac {y^2}{10}\) = 1
(iii) \(\frac {x^2}{25}\) – \(\frac {y^2}{144}\) = 1
(iv) \(\frac {y^2}{16}\) – \(\frac {x^2}{9}\) = 1
Solution:
(i) \(\frac{x^{2}}{25}+\frac{y^{2}}{9}\) = 1
It is of the form \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, which is an ellipse
Here a² = 25, b² = 9
a = 5, b = 3
e² = \(\frac{a^{2}-b^{2}}{a^{2}}=\frac{25-9}{25}=\frac{16}{25}\) ⇒ e = \(\frac{4}{5}\)
Now e = \(\frac{4}{5}\) and a = 5 ⇒ ae = 4 and \(\frac{a}{e}=\frac{5}{4 / 5}=\frac{25}{4}\)
Here the major axis is along x axis
∴ Centre = (0, 0)
Foci = (± ae, 0) = (± 4, 0)
Vertices = (± a, 0) = (±5, 0)
Equation of directrix x = ± \(\frac{a}{e}\) (ie.,) x = ± \(\frac{25}{4}\)

(ii) \(\frac {x^2}{3}\) + \(\frac {y^2}{10}\) = 1
It is an ellipse. The major axis is along y axis

a² = 10 b² = 3
a = \(\sqrt {10}\) b = √3
c² = a² – b²
= 10 – 3 = 7
c = √7
ae = √7 .
\(\sqrt {10}\) = √7
e = \(\sqrt {\frac{7}{10}}\)
(a) Centre (0, 0)
(b) Vertex (0, ±a) = (0, ±\(\sqrt {10}\))
(c) Foci (0, ±c) – (0, ±√7)
(d) Equation of the directrix a
y = ±\(\frac{a}{e}\)
= ±\(\frac{\sqrt {10}}{√7}\).\(\sqrt {10}\) = ±\(\frac {10}{√7}\)
y = ±\(\frac {10}{√7}\)

(iii) \(\frac {x^2}{25}\) – \(\frac {y^2}{144}\) = 1
It is Hyperbola. The transverse axis the x axis.

a² = 25; b² = 144
a = 5; b = 12
c² = a² + b²
= 25 + 144 = 169
c = 13
ae = 13
5e = 13
e = \(\frac {13}{5}\)
(a) Centre (0, 0)
(b) Vertex (± a, 0) = (± 5, 0)
(c) Foci (± c, 0) = (± 13, 0)
(d) Equation of the directrix
x = ±\(\frac {a}{e}\) = ±\(\frac {5}{\frac{13}{5}}\) = ±\(\frac {25}{13}\)
x = ±\(\frac {25}{13}\)

(iv) \(\frac {y^2}{16}\) – \(\frac {x^2}{9}\) = 1
It is Hyperbola. The transverse axis the y axis.

a² = 16; b² = 9
a = 4; b = 3
c² = a² + b²
= 16 + 6 = 25
c = 5
ae = 5
4e = 5
e = \(\frac {5}{4}\)
(a) Centre (0, 0)
(b) Vertex (0, ±a) = (0, ±4)
(c) Foci (0, ±ae) = (0, ±5)
(d) Equation of the directrix
y = ±\(\frac {a}{e}\) = ±\(\frac {4}{\frac{5}{4}}\) = ±\(\frac {16}{5}\)
y = ±\(\frac {16}{5}\)

Question 6.
Prove that the length of the latns rectum of the hyperbola \(\frac {x^2}{a^2}\) – \(\frac {y^2}{b^2}\) = 1 is \(\frac {2b^2}{a}\)
Solution:
The latus rectum LL’ of an hyperbola \(\frac {x^2}{a^2}\) – \(\frac {y^2}{b^2}\) = 1 passes through S(ae, 0)
Hence L is (ae, y₁)

Hence proved

Question 7.
Show that the absolute value of the difference of the focal distances of any point P on the hyperbola is the length of its transverse axis.
Solution:

Let P be a point on the hyperbola.
Definition of conic
\(\frac {SP}{PM}\) = e; \(\frac {S’P}{PM’}\) = e
SP = e(PM) ……..(1)
S’P = e (PM’) ……….(2)
(2) – (1) ⇒ S’P – SP = e PM’- e PM
= e(PM’ – PM)
= e MM’
= e ZZ’
[∵ MM’ = ZZ’ = \(\frac {2a}{e}\) ]
= e(\(\frac {2a}{e}\))
S’P – SP = 2a (constant)
= length of the transverse axis.

Question 8.
Identify the type of conic and find centre, foci, vertices and directrices of each of the following:

(v) 18x² + 12y² – 144x + 48y + 120 = 0
(vi) 9x² – y² – 36x – 6y + 18 = 0
Solution:
(i) \(\frac {(x-3)^2}{225}\) + \(\frac {(y-4)^2}{289}\) = 1

It is an ellipse. The major axis is parallel to y axis
a² = 289, b² = 225
a = 17, b = 15
c² = a² – b²
= 289 – 225 = 64
c = 8
ae = 8
17e = 8
e = \(\frac {8}{17}\)
Centre (h, k) = (3, 4)
Vertices (h, ±a + k) = (3, 17 + 4) & (3, -17 + 4)!
= (3, 21) and (3, -13)
Foci (h + 0, ± c + k) = (3, 8 + 4) & (3, -8 + 4)
= (3, 12) and (3, -4)

(ii) \(\frac {(x+1)^2}{100}\) + \(\frac {(y-2)^2}{64}\) = 1
It is an ellipse. The major axis is parallel to the x-axis.
a² = 100, b² = 64
a = 10, b = 8
c² = a² – b²
= 100 – 64 = 36
c = 6
ae = 6
10 e = 6
e = \(\frac {6}{10}\) = \(\frac {3}{5}\)
centre (h, k) = (-1, 2)
vertices (h±a, k) = (-1±10, 2)
= (-1+10, 2) & (-1-10, 2)
= (9, 2) & (-11, 2)
foci (h±c, k) = (-1±6, 2)
= (-1+6, 2) & (-1-6, 2)
= (5, 2) & (-7, 2)
directrix x = ±\(\frac {a}{e}\) + h

(iii) \(\frac {(x+3)^2}{225}\) + \(\frac {(y-4)^2}{64}\) = 1
It is an hyperbola. The transverse axis is parallell to x axis.
a² = 225, b² = 64
a = 15, b = 8
c² = a² – b²
= 225 + 64
c² = 289
c = 17
ae = 17
5e = 17
e = \(\frac {17}{15}\)
centre (h, k) = (-3, 4)
vertices (h±a, k) = (-3±15, 4)
= (-3+15, 4) & (-3-15, 4)
= (12, 4) & (-18, 4)
foci (h±c, k) = (-3±17, 4)
= (-3+17, 4) & (-3-17, 4)
= (14, 4) & (-20, 4)
directrix x = ±\(\frac {a}{e}\) + h

(iv) \(\frac {(y-2)^2}{25}\) + \(\frac {(x+1)^2}{16}\) = 1
It is an hyperbola. The transverse axis is parallell to y axis.
a² = 25, b² = 16
a = ±5, b = 4
c² = a² + b²
= 25 + 16
= 41
c = \(\sqrt {41}\)
ae = \(\sqrt {41}\)
5 e = \(\sqrt {41}\)
e = \(\frac {\sqrt {41}}{5}\)
centre (h, k) = (-1, 2)
vertices (h, ±a + k) = (-1, ±5 + 2)
= (-1, 5 + 2) & (-1, -5 + 2)
= (-1, 7) & (-1, -3)
foci (h, ±c + k) = (-1, ±\(\sqrt {41}\) + 2)
= (-1, \(\sqrt {41}\) + 2) & (-1, –\(\sqrt {41}\) + 2)
directrix x = ±\(\frac {a}{e}\) + k

(v) 18x² + 12y² – 144x + 48y + 120 = 0
18x² – 144x + 12y² + 48y = -120
18 (x² – 8x) + 12 (y² + 4y) = -120
18 (x – 4)² + 12 (y + 2)² = -120 + 288 + 48
18(x – 4)² + 12 (y + 2)² = 216
\(\frac {18(x-4)^2}{216}\) + \(\frac {12(y+2)^2}{216}\) = 1
\(\frac {(x-4)^2}{12}\) + \(\frac {(y+2)^2}{18}\) = 1
It is an ellipse. The major axis is parallell to y axis.
a² = 18, b² = 12
a = \(\sqrt {18}\), b = 2√3
= 3 √2
c² = a² + b²
= 18 – 12
= 6
c = √6
ae = √6
3√2 e = √6
e = \(\frac {√6}{3√2}\) = \(\frac {√3}{3}\) = \(\frac {1}{√3}\)
centre (h, k) = (4, -2)
vertices (h, ±a + k) = (4, ±3√2 – 2)
= (4, 3√2 – 2) & (4, -3√2 – 2)
foci (h, ±c + k) = (4, ±√6 – 2)
= (4, ±√6 – 2) & (4, -√6 – 2)
directrix y = ±\(\frac {a}{e}\) + k
= ±\(\frac {3√2}{1}\) – 2
= ±3√6 – 2
y = 3√6 – 2 & y = -3√6 – 2

(vi) 9x² – y² – 36x – 6y + 18 = 0
9x² – 36x – y² – 6y = – 18
9(x² – 4x) – (y² + 6y) = -18
9(x – 2)² – (y + 3)² = -18 + 36 – 9
9(x – 2)² – (y + 3)² = 9
\(\frac {(x-2)^2}{1}\) – \(\frac {(y+3)^2}{9}\) = 1
It is hyperbola. The transverse axis is parallel to x axis.
a² = 1; b² = 9
a = 1; b = 3
c² = a² + b²
= 1 + 9
= 10
c = \(\sqrt {10}\)
ae = \(\sqrt {10}\)
e = \(\sqrt {10}\)
centre (h, k) = (2, -3)
vertices (h ± a, k) = (2 ± 1, -3)
= (2 + 1, -3) & (2 – 1, -3)
= (3, -3) & (1, -3)
foci (h ± c, k) = (2 ±\(\sqrt {10}\), -3)
= (2 + \(\sqrt {10}\), -3) & (2 –\(\sqrt {10}\), -3)
directrix x = ±\(\frac {a}{e}\) + h
= ±\(\frac {1}{\sqrt {10}}\) + 2 & x = –\(\frac {1}{\sqrt {10}}\) + 2

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.1 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.1

Question 1.
Obtain the equation of the circles with a radius of 5 cm and touching the x-axis at the origin in a general form.
Solution:

Given radius = 5 cm and the circle is touching x axis
So centre will be (0, ± 5) and radius = 5
The equation of the circle with centre (0, ± 5) and radius 5 units is
(x – 0)² + (y ± 5)² = 5²
(i.e) x² + y² ± 10 y + 25 – 25 = 0
(i.e) x² + y² ± 10y = 0

Question 2.
Find the equation of the circle with centre (2, – 1) and passing through the point (3, 6) in standard form.
Solution:
Centre = (2, -1) = (h, k)
Passing through the point (3, 6)
Equation of the circle (x – h)² + (y – k)² = r² ………. (1)
(3 – 2)² + (6 + 1)² = r²
1² + 7² = r²
1 + 49 = r²
r² = 50
(1) ⇒ (x – 2)² + (y + 1)² = 50

Question 3.
Find the equation of circles that touch both the axes and pass-through (-4, -2) in a general form.
Solution:

Since the circle touches both the axes, its centre will be (r, r) and the radius will be r.
Here centre = C = (r, r) and point on the circle is A = (-4, -2)
CA = r ⇒ CA² = r²
(i.e) (r + 4)² + (r + 2)² = r²
⇒ r² + 8r +16 + r² + 4r + 4 – r² = 0
(i.e) r² + 12r + 20 = 0
(r + 2) (r + 10) = 0
⇒ r = -2 or -10
When r = -2, the equation of the circle will be (x + 2)² + (y + 2)² = 2²
(i.e) x² + y² + 4x + 4y + 4 = 0
When r = -10, the equation of the circle will be (x + 10)² + (y + 10)² = 10²
(i.e) x² + y² + 20x + 20y + 100 = 0

Question 4.
Find the equation of the circles with centre (2, 3) and passing through the intersection of the lines 3x – 2y – 1 =0 and 4x + y – 27 = 0.
Solution:
centre (2, 3) = (h, k)
Point of intersection
Solve 3x – 2y – 1 = 0 ………. (1)
4x + y – 27 = 0 ……… (2)
(1) ⇒ 3x – 2y = 1
(2) × 2 ⇒ 8x + 2y = 54
11x = 55
x = 5
put in (1)
15 – 2y – 1 = 0
14 = 2y
y = 7
Passing-through point is (5, 7)
Equation of circle be (x – h)² + (y – k)² = r² ……….(3)
(5 – 2)² + (7 – 3)² = r²
3² + 4² = r²
r² = 25
∴ (3) ⇒ (x – 2)² + (y – 3)² = 25
x² – 4x + 4 + y² – 6y + 9 – 25 = 0
x² + y² – 4x – 6y – 12 = 0

Question 5.
Obtain the equation of the circle for which (3, 4) and (2, -7) are the ends of a diameter.
Solution:
The equation of a circle with (x₁ , y₁) and (x₂ , y₂ ) as end points of a diameter is
(x – x₁ )(x – x₂) + (y – y₁ )(y – y₂) = 0
Here the end points of a diameter are (3, 4) and (2, -7)
So equation of the circle is (x – 3 )(x – 2 ) + (y – 4) (y + 7.) = 0
x² + y² – 5x + 37 – 22 = 0

Question 6.
Find the equation of the circle through the points (1, 0), (-1, 0) and (0, 1).
Solution:
Let the general equation of the circle be
x² + y² + 2gx + 2fy + c = 0
It passes through the points (1, 0), (-1, 0) and (0,1)
1 + 0 + 2g + c = 0
2g + c = -1 ………(1)
1 + 0 – 2g + c = 0
-2g + c = -1 …………(2)
0 + 1 + 0 + 2f + c = 0
2f + c = -1
(1) + (2) ⇒ 2c = -2
c = -1
substitute in eqn (1)
2g – 1 = -1
2g = 0
g = 0
substitute in eqn (3)
2f – 1 = -1
2f = -1 + 1
2f = 0
f = 0
Therefore, the required equation of the circle
x² + y² – 1 = 0

Question 7.
A circle of area 9π square units has two of its diameters along the lines x + y = 5 and: x – y = 1. Find the equation of the circle.
Solution:

Area of the circle = 9π
(i.e) πr² = 9π
⇒ r² = 9 ⇒ r = 3
(i.e) radius of the circle = r = 3
The two diameters are x + y = 5 and x – y = 1
The point of intersection of the diameter is the centre of the circle = C
To find C: Solving x + y = 5 ……… (1)
x – y = 1 ………. (2)
(1) + (2) ⇒ 2x = 6 ⇒ x = 3
Substituting x = 3 in (1) we get
3 + y = 5 ⇒ y = 5 – 3 = 2
∴ Centre = (3, 2) and radius = 3
So equation of the circle is (x – 3)² + (y – 2)² = 3²
(i.e) x² + y² – 6x – 4y + 4 = 0

Question 8.
If y = 2√2 x + c is a tangent to the circle x² + y² = 16, find the value of c.
Solution:
The condition of the line y = mx + c to be a tangent to the circle x² + y² = a² is
c² = a²( 1 + m²)
a² = 16; m = 2√2 ⇒ m² = 4 × 2 = 8
c² = 16(1+8)
c² = 16(9)
c = ±4 × 3 = ±12
∴ c = ± 12.

Question 9.
Find the equation of the tangent and normal to the circle x² + y² – 6x + 6y – 8 = 0 at (2, 2).
Solution:
The equation of the tangent to the circle x² + y² + 2 gx + 2fy + c = 0 at (x₁, y₁) is
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 9
So the equation of the tangent to the circle
x² + y² – 6x + 6y – 8 = 0 at (x₁, y₁) is
xx₁ + yy₁ – \(\frac{6\left(x+x_{1}\right)}{2}+\frac{6\left(y+y_{1}\right)}{2}\) – 8 = 0
(i.e) xx₁ + yy₁ – 3(x + x₁) + 3(y + y₁) – 8 = 0
Here (x₁, y₁) = (2, 2)
So equation of the tangent is
x(2) + y(2) – 3(x + 2) + 3(y + 2) – 8 = 0
(.i.e) 2x + 2y – 3x – 6 + 3y + 6 – 8 = 0
(i.e) -x + 5y – 8 = 0 or x – 5y + 8=0
Normal is a line ⊥r to the tangent
So equation of normal circle be of the form 5x + y + k = 0
The normal is drawn at (2, 2)
⇒ 10 + 2 + k = 0 ⇒ k = -12
So equation of normal is 5x + y – 12 = 0

Question 10.
Determine whether the points (- 2, 1), (0, 0) and s (- 4, – 3) lie outside, on or inside the circle x² + y² – 5x + 2y – 5 = 0.
Solution:
x² + y² – 5x + 2y – 5 = 0
(i) At (-2, 1) ⇒ (-2)² + 1² – 5(-2) + 2(1) – 5
= 4 + 1 + 10 + 2 – 5 = 12 > 0
∴ (-2, 1) lies outside the circle.

(ii) At(0, 0) ⇒ 0 + 0 – 0 + 0 – 5 = -5 < 0
(0, 0) lies inside the circle.

(iii) At (-4, -3) ⇒ (-4)² + (- 3)² – 5(-4) + 2(-3) – 5 = 16 + 9 + 20 – 6 – 5 = 34 > 0
(-4, -3) lies outside the circle.

Question 11.
Find the centre and radius of the following circles.
(i) x² + (y + 2)² = 0
(ii) x² + y² + 6x – 4y + 4 = 0
(iii) x² + y² – x + 2y – 3 = 0
(iv) 2x² + 2y² – 6x + 4y + 2 = 0
Solution:
(i) x² + (y + 2)² = 0
(i.e) x² + y² + 4y + 4 = 0
Comparing this equation with the general form x² + y² + 2gx + 2fy + c = 0
we get 2g = 0 ⇒ g = 0
2f = 4 ⇒ f= 2 and c = 4
Now centre = (-g, -f) = (0, -2)
Radius = r = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{0+4-4}\)
∴ Centre = (0, -2) and radius = 0

(ii) x² + y² + 6x – 4y + 4 = 0
Comparing with the general form we get
2g = 6, 2f = -4
⇒ g = 3, /= -2 and c = 4
Centre = (-g, -f) = (-3, 2)
Radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{9+4-4}\)= 3
∴ Centre = (-3, 2) and radius = 3

(iii) x² + y² – x + 2y – 3 = 0
2g = -1; 2f = 2; c = -3
g = \(\frac{-1}{2}\) f = 1
Centre (-g, -f) = (\(\frac{1}{2}\), -1)
Radius = \(\sqrt{g^2+f^2-c}\) = \(\sqrt{\frac{1}{4}+1+3}\)
\(\sqrt{\frac{1+4+12}{4}}\)
\(\sqrt{\frac{17}{4}}\) = \(\frac{\sqrt{17}}{2}\)

(iv) 2x² + 2y² – 6x + 4y + 2 = 0
(÷ by 2) ⇒ x² + y² – 3x + 2y + 1 =0
Comparing this equation with the general form of the circle we get
2g = -3, 2f= 2
g = \(-\frac{3}{2}\), g= 1 and c = 1
So centre = (-g, -f) = (\(\frac{3}{2}\), -1)
and radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{\frac{9}{4}+1-1}=\frac{3}{2}\)
∴ Centre = (\(\frac{3}{2}\), -1) and radius = \(\frac{3}{2}\)

Question 12.
If the equation 3x² + (3 – p) xy + qy² – 2px = 8pq represents a circle, find p and q. Also determine the centre and radius of the circle.
Solution:
3x² + (3 – p) xy + qy² – 2px = 8pq represent a circle means,
Co-efficient of x² = co-efficient of y²
3 = q ⇒ q = 3
Co-efficient of xy = 0
3 – p = 0 ⇒ p = 3
3x² + 3y² – 6x = 8 (3)(3)
3x² + 3y² – 6x – 72 = 0
(÷3) x² + y² – 2x – 24 = 0
2g = -2; 2f = 0; c = -24
g = -1 f = 0
Centre (-g, -f) = (1, 0)
Radius = \(\sqrt{g^2+f^2-c}\) = \(\sqrt{1+0+24}\)
= \(\sqrt{25}\) = 5