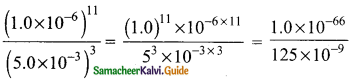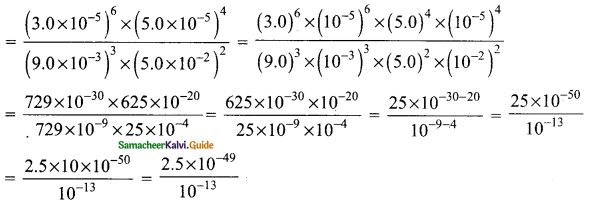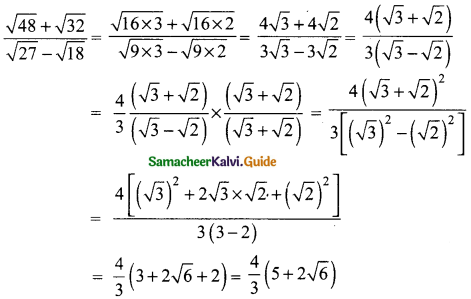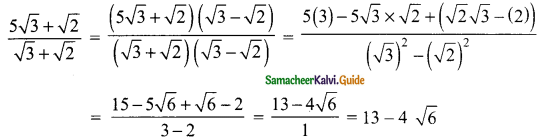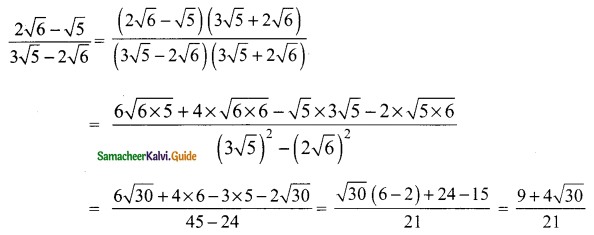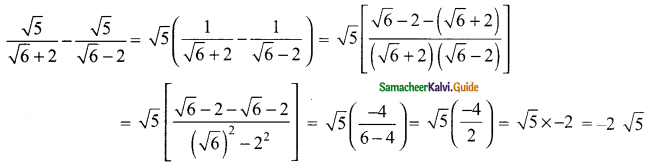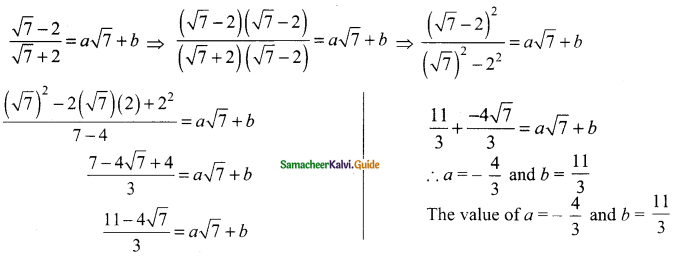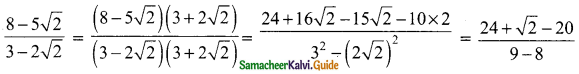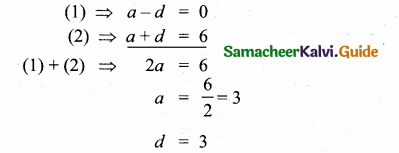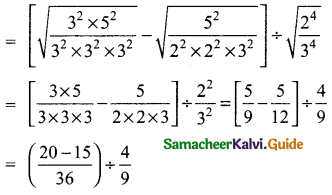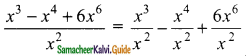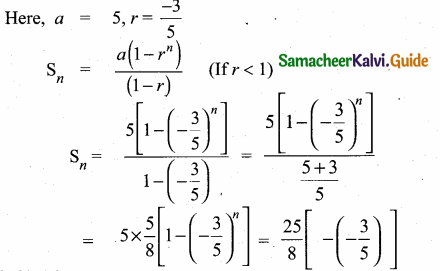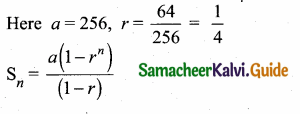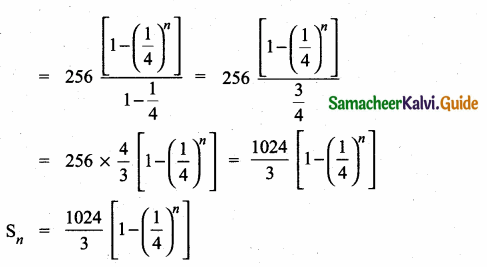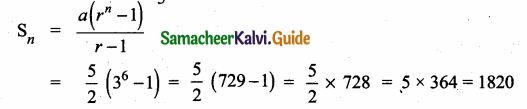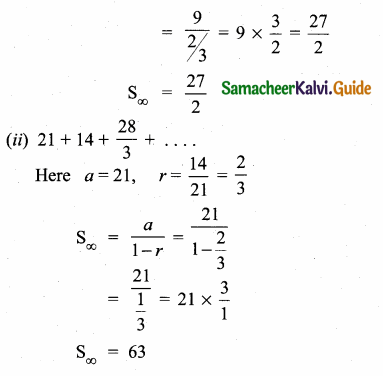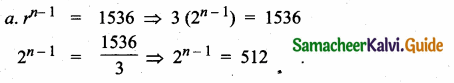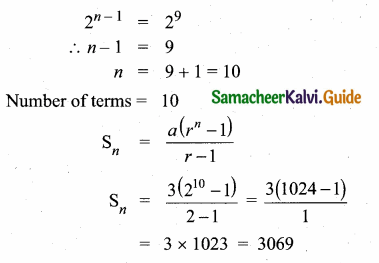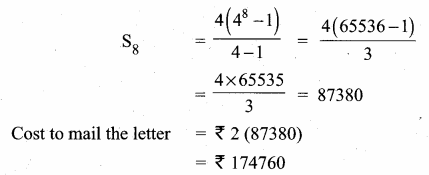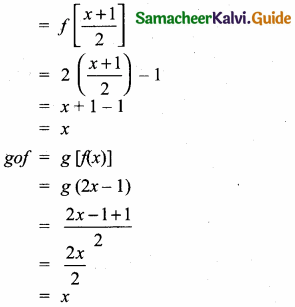Bhagya

Students can download Maths Chapter 2 Numbers and Sequences Ex 2.7 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.7

Question 1.
Which of the following sequences are in G.P?
(i) 3,9,27,81,…
(ii) 4,44,444,4444,…
(iii) 0.5,0.05,0.005,
(iv) \(\frac { 1 }{ 3 } \),\(\frac { 1 }{ 6 } \),\(\frac { 1 }{ 12 } \), ………….
(v) 1, -5, 25,-125,…
(vi) 120, 60, 30, 18,…
(vii) 16, 4, 1, \(\frac { 1 }{ 4 } \), ……….
Answer:

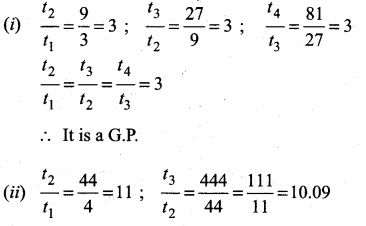
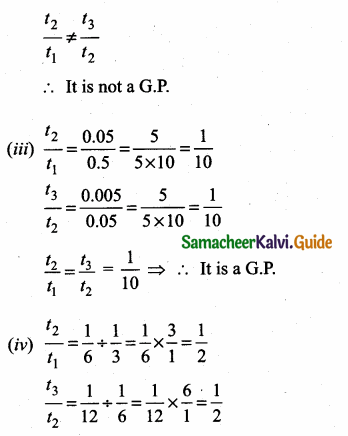
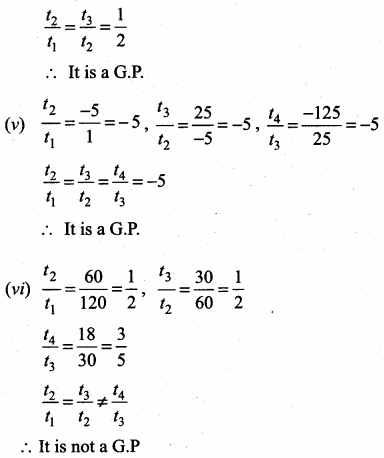
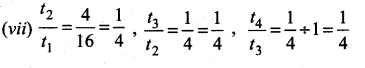
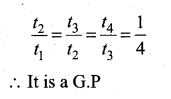
Question 2.
Write the first three terms of the G.P. whose first term and the common ratio are given below.
(i) a = 6, r = 3
Answer:
a = 6, r = 3
ar = 6 × 3 = 18,
ar² = 6 × 9 = 54
The three terms are 6, 18 and 54

(ii) a = \(\sqrt { 2 }\), r = \(\sqrt { 2 }\).
Answer:
ar = \(\sqrt { 2 }\) × \(\sqrt { 2 }\) = 2,
ar² = \(\sqrt { 2 }\) × 2 = 2 \(\sqrt { 2 }\)
The three terms are \(\sqrt { 2 }\), 2 and 2\(\sqrt { 2 }\)

(iii) a = 1000, r = \(\frac { 2 }{ 5 } \)
Answer:
ar = 1000 × \(\frac { 2 }{ 5 } \) = 400,
ar² = 1000 × \(\frac { 4 }{ 25 } \) = 40 × 4 = 160
The three terms are 1000,400 and 160.

Question 3.
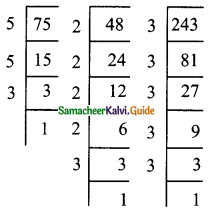
In a G.P. 729, 243, 81,… find t₇.
Answer:
The G.P. is 729, 243, 81,….

Question 4.
Find x so that x + 6, x + 12 and x + 15 are consecutive terms of a Geometric Progression
Solution:
G.P = x + 6, x + 12, x + 15
In G.P r = \(\frac{t_{2}}{t_{1}}=\frac{t_{3}}{t_{2}}\)
\(\frac{x+12}{x+6}=\frac{x+15}{x+12}\)
(x + 12)² = (x + 6) (x + 5)
x² + 24x + 144 = x² + 6x + 15x + 90
24x – 21x = 90 – 144
3x = -54
x = \(\frac { -54 }{ 3 } \) = -18
x = -18

Question 5.
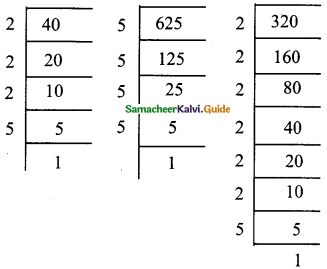
Find the number of terms in the following G.P.

(i) 4,8,16,…,8192?
Answer:
Here a = 4; r = \(\frac { 8 }{ 4 } \) = 2
t_n = 8192

a . r^n-1 = 8192 ⇒ 4 × 2^n-1 = 8192
2^n-1 = \(\frac { 8192 }{ 4 } \) = 2048
2^n-1 = 2¹¹ ⇒ n – 1 = 11
n = 11 + 1 ⇒ n = 12
Number of terms = 12

(ii) \(\frac { 1 }{ 3 } \), \(\frac { 1 }{ 9 } \), \(\frac { 1 }{ 27 } \), ……………, \(\frac { 1 }{ 2187 } \)
Answer:
a = \(\frac { 1 }{ 3 } \) ; r = \(\frac { 1 }{ 9 } \) ÷ \(\frac { 1 }{ 3 } \) = \(\frac { 1 }{ 9 } \) × \(\frac { 3 }{ 1 } \) = \(\frac { 1 }{ 3 } \)

t_n = \(\frac { 1 }{ 2187 } \)
a. r^n-1 = \(\frac { 1 }{ 2187 } \)

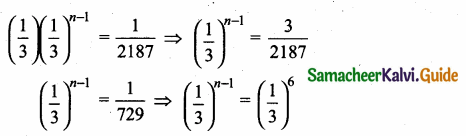
n – 1 = 6 ⇒ n = 6 + 1 = 7
Number of terms = 7

Question 6.
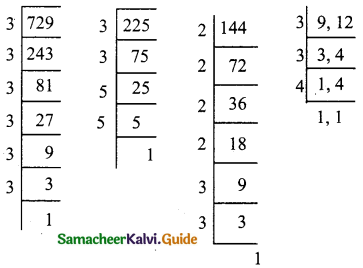
In a G.P. the 9^th term is 32805 and 6^th term is 1215. Find the 12^th term.
Answer:
Given, 9^th term = 32805
a. r^n-1 = \(\frac { 1 }{ 2187 } \)
t₉ = 32805 [t_n = ar^n-1]
a.r⁸ = 32805 …..(1)
6^th term = 1215
a.r⁵ = 1215 …..(2)
Divide (1) by (2)
\(\frac{a r^{8}}{a r^{5}}\) = \(\frac { 32805 }{ 1215 } \) ⇒ r³ = \(\frac { 6561 }{ 243 } \)
= \(\frac { 2187 }{ 81 } \) = \(\frac { 729 }{ 27 } \) = \(\frac { 243 }{ 9 } \) = \(\frac { 81 }{ 3 } \)
r³ = 27 ⇒ r³ = 3³
r = 3
Substitute the value of r = 3 in (2)
a. 3⁵ = 1215
a × 243 = 1215
a = \(\frac { 1215 }{ 243 } \) = 5
Here a = 5, r = 3, n = 12
t₁₂ = 5 × 3^(12-1)
= 5 × 3¹¹
∴ 12^th term of a G.P. = 5 × 3¹¹

Question 7.
Find the 10th term of a G.P. whose 8^th term is 768 and the common ratio is 2.
Solution:
t₈ = 768 = ar⁷
r = 2
t₁₀ = ar⁹ = ar⁷ × r × r
= 768 × 2 × 2 = 3072

Question 8.
If a, b, c are in A.P. then show that 3^a, 3^b, 3^c are in G.P.
Answer:
a, b, c are in A.P.
t₂ – t₁ = t₃ – t₂
b – a = c – b
2b = a + c …..(1)
3^a, 3^b, 3^c are in G.P.

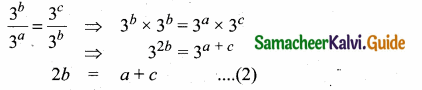
From (1) and (2) we get
3^a, 3^b, 3^c are in G.P.

Question 9.
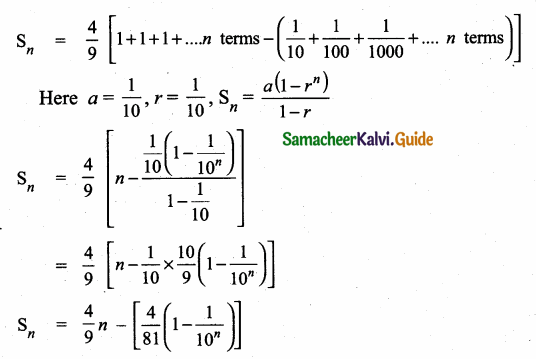
In a G.P. the product of three consecutive terms is 27 and the sum of the product of two terms taken at a time is \(\frac { 57 }{ 2 } \). Find the three terms.
Answer:
Let the three terms of the G.P. be \(\frac { a }{ r } \), a, ar
Product of three terms = 27
\(\frac { a }{ r } \) × a × ar = 27
a³ = 27 ⇒ a³ = 3³
a = 3
Sum of the product of two terms taken at a time is \(\frac { 57 }{ 2 } \)

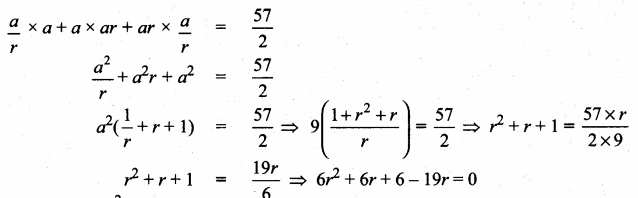
6r² – 13r + 6 = 0
6r² – 9r – 4r + 6 = 0
3r (2r – 3) -2(2r – 3) = 0
(2r – 3) (3r – 2) = 0
2r – 3 = 0 or 3r – 2 = 0
2r = 3 (or) 3r – 2 = 0
r = \(\frac { 3 }{ 2 } \) (or) r = \(\frac { 2 }{ 3 } \)

∴ The three terms are 2, 3 and \(\frac { 9 }{ 2 } \) or \(\frac { 9 }{ 2 } \), 3 and 2

Question 10.
A man joined a company as Assistant Manager. The company gave him a starting salary of ₹60,000 and agreed to increase his salary 5% annually. What will be his salary after 5 years?
Answer:
Starting salary (a) = ₹ 60000
Increased salary = 5% of starting salary
= \(\frac { 5 }{ 100 } \) × 60000
= ₹ 3000
Starting salary for the 2nd year = 60000 + 3000
= ₹ 63000
Year increase = 5% of 63000
= \(\frac { 5 }{ 100 } \) × 63000
= ₹ 3150
Starting salary for the 3^rd year = 63000 + 3150
= ₹ 66150
60000, 63000, 66150,…. form a G.P.
a = 60000; r = \(\frac { 63000 }{ 60000 } \) = \(\frac { 63 }{ 60 } \) = \(\frac { 21 }{ 20 } \)
t_n = an^n-1
t₅ = (60000) (\(\frac { 21 }{ 20 } \))⁴
= 60000 × \(\frac { 21 }{ 20 } \) × \(\frac { 21 }{ 20 } \) × \(\frac { 21 }{ 20 } \) × \(\frac { 21 }{ 20 } \)
= \(\frac{6 \times 21 \times 21 \times 21 \times 21}{2 \times 2 \times 2 \times 2}\)
= 72930.38
5% increase = \(\frac { 5 }{ 100 } \) × 72930.38
= ₹ 3646.51
Salary after 5 years = ₹ 72930.38 + 3646.51
= ₹ 76576.90
= ₹ 76577

Question 11.
Sivamani is attending an interview for a job and the company gave two offers to him. Offer A: ₹20,000 to start with followed by a guaranteed annual increase of 6% for the first 5 years.
Offer B: ₹22,000 to start with followed by a guaranteed annual increase of 3% for the first 5 years.
What is his salary in the 4^th year with respect to the offers A and B?
Answer:
Starting salary (a) = ₹ 20,000
Annual increase = 6% of 20000
= \(\frac { 5 }{ 100 } \) × 20000
= ₹ 1200
Salary for the 2nd year = ₹ 20000 + 1200
= ₹ 21200
Here a = 20,000; r = \(\frac { 21200 }{ 20000 } \) = \(\frac { 212 }{ 200 } \) = \(\frac { 106 }{ 100 } \) = \(\frac { 53 }{ 50 } \)
n = 4 years
t_n = ar^n-1

Salary at the end of 4^th year = 23820

For B
Starting salary = ₹ 22000
(a) = 22000
Annual increase = 3% of 22000
= \(\frac { 3 }{ 100 } \) × 22000
= ₹ 660
Salary for the 2nd year = ₹ 22000 + ₹ 660
= ₹ 22,660
Here a = 22000; r = \(\frac { 22660 }{ 22000 } \)
= \(\frac { 2266 }{ 2200 } \) = \(\frac { 1133 }{ 1100 } \) = \(\frac { 103 }{ 100 } \)
Salary at the end of 4th year = 22000 × (\(\frac { 103 }{ 100 } \))^4-1
= 22000 × (\(\frac { 103 }{ 100 } \))³
= 22000 × \(\frac { 103 }{ 100 } \) × \(\frac { 103 }{ 100 } \) × \(\frac { 103 }{ 100 } \)

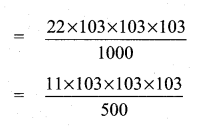
= 24039.99 = 24040
4^th year Salary for A = ₹ 23820 and 4^th year Salary for B = ₹ 24040

Question 12.
If a, b, c are three consecutive terms of an A.P. and x, y, z are three consecutive terms of a G.P. then prove that x^b-c × y^c-a × z^a-b = 1
Answer:
a, b, c are three consecutive terms of an A.P
∴ a = a, b = a + dand c = a + 2d respectively ….(1)
x, y, z are three consecutive terms of a G.P
∴ x = x, y = xr, z = xr² respective ……(2)
L.H.S = x^b-c × y^c-a × z^a-b ( Substitute the values from 1 and 2 we get)

L.H.S = R.H.S
Hence it is proved

Students can download Maths Chapter 2 Real Numbers Ex 2.8 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.8

Question 1.
Represent the following numbers in the scientific notation:
(i) 569430000000
(ii) 2000.57
(iii) 0.0000006000
(iv) 0.0009000002
Solution:
(i) 569430000000 = 5.6943 × 10¹¹
(ii) 2000.57 = 2.00057 × 10³
(iii) 0.0000006000 = 6.0 × 10^-7
(iv) 0.0009000002 = 9.000002 × 10^-4

Question 2.
Write the following numbers in decimal form:
(i) 3.459 × 10⁶
(ii) 5.678 × 10⁴
(iii) 1.00005 × 10^-5
(iv) 2.530009 × 10^-7
Solution:
(i) 3.459 × 10⁶
= 3459000
(ii) 5.678 × 10⁴
= 56780
(iii) 1.00005 × 10^-5
= 0.0000100005
(iv) 2.530009 × 10^-7
= 0.0000002530009

Question 3.
Represent the following numbers in scientific notation:
(i) (300000)² × (20000)⁴
(ii) (0.000001)¹¹ ÷ (0.005)³
(iii) {(0.00003)⁶ × (0.00005)⁴} ÷ {(0.009)³ × (0.05)²}
Solution:
(i) (300000)² × (20000)⁴ = (3 × 10⁵)² × (2 × 10⁴)⁴
= 3² × (10⁵)² × 2⁴ × (10⁴)⁴
= 9 × 10¹⁰ × 16 × 10¹⁶
= 9 × 16 × 10^10-16
= 144 × 10²⁶
= 1.44 × 10²⁸

(ii) (0.000001)¹¹ ÷ (0.005)³

0.008 × 10^-66+9
= 8.0 × 10^-3 × 10^-57
= 8.0 × 10^-3-57
= 8.0 × 10^-60

(iii) {(0.00003)⁶ × (0.00005)⁴} ÷ {(0.009)³ × (0.05)²}

= 2.5 × 10^-49+13
= 2.5 × 10^-36

Question 4.
Represent the following information in scientific notation:
(i) The world population is nearly 7000,000,000.
(ii) One light year means the distance 9460528400000000 km.
(iii) Mass of an electron is 0.000 000 000 000 000 000 000 000 000 00091093822 kg.
Solution:
(i) World population = 7.0 × 10⁹
(ii) Distance = 9.4605 × 10¹⁵ km.
(iii) Mass of an electron = 9.1093822 × 10^-31 kg

Question 5.
Simplify:
(2.75 × 10⁷) + (1.23 × 10⁸)
(ii) (1.598 × 10¹⁷) – (4.58 × 10¹⁵)
(iii) (1.02 × 10¹⁰) × (1.20 × 10^-3)
(iv) (8.41 × 10⁴) ÷ (4.3 × 10⁵)
Solution:
(i) (2.75 × 10⁷) + (1.23 × 10⁸) = 27500000 + 123000000

= 150500000
= 1.505 × 10⁸

(ii) (1.598 × 10¹⁷) – (4.58 × 10¹⁵) = 1552,20000000000000

= 1.5522 × 10¹⁷

(iii) (1.02 × 10¹⁰) × (1.20 × 10^-3) = 1.02 × 1.20 × 10¹⁰ × 10^-3
=1.224 × 10⁷

(iv) (8.41 × 10⁴) ÷ (4.3 × 10⁵) = \(\frac{8.41×10^{4}}{4.3×10^{5}}\)
= \(\frac{8.41}{4.3}\) × 10^4-5
= \(\frac{8.41}{4.3}\) × 10^-1
= 1.9558139 × 10^-1

Students can download Maths Chapter 2 Real Numbers Ex 2.7 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.7

Question 1.
Rationalise the denominator:
(i) \( \frac{1}{\sqrt{50}}\)
(ii) \( \frac{5}{3\sqrt{5}}\)
(iii) \( \frac{\sqrt{75}}{\sqrt{18}}\)
(iv) \( \frac{3\sqrt{5}}{\sqrt{6}}\)
Solution:
(i) \( \frac{1}{\sqrt{50}}\) = \(\frac{1}{\sqrt{25 \times 2}}=\frac{1}{5 \sqrt{2}}=\frac{1}{5 \sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{5 \times 2}=\frac{\sqrt{2}}{10}\)

(ii) \( \frac{5}{3\sqrt{5}}\) = \(\frac{5}{3 \sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}}=\frac{5 \sqrt{5}}{3 \times 5}=\frac{\sqrt{5}}{3}\)

(iii) \( \frac{\sqrt{75}}{\sqrt{18}}\) = \(\frac{\sqrt{3 \times 25}}{\sqrt{2 \times 9}}=\frac{5 \sqrt{3}}{3 \sqrt{2}}=\frac{5 \sqrt{3}}{3 \sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{5 \sqrt{6}}{3 \times 2}=\frac{5 \sqrt{6}}{6}\)

(iv) \( \frac{3\sqrt{5}}{\sqrt{6}}\) = \( \frac{3 \sqrt{5}}{\sqrt{6}} \times \frac{\sqrt{6}}{\sqrt{6}}=\frac{3 \sqrt{30}}{6}=\frac{\sqrt{30}}{2} \)

Question 2.
Rationalise the denominator and simplify:
(i) \(\frac{\sqrt{48}+\sqrt{32}}{\sqrt{27}-\sqrt{18}}\)
Solution:

(ii) \(\frac{5\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}\)
Solution:

(iii) \(\frac{2\sqrt{6}-\sqrt{5}}{3\sqrt{5}-2\sqrt{6}}\)
Solution:

(iv) \(\frac{\sqrt{5}}{\sqrt{6}+2} – \frac{\sqrt{5}}{\sqrt{6}-2}\)
Solution:

Question 3.
Find the value of a and b if \(\frac{\sqrt{7}-2}{\sqrt{7}+2} = a\sqrt{7} + b\).
Solution:

Question 4.
If x = \(\sqrt{7}\) + 2, then find the value of x² + \(\frac{1}{x^2}\)
Solution:
\(\sqrt{7}\) + 2 ⇒ x² = \((\sqrt{5}+2)^{2}\)
= \((\sqrt{5})^{2}\) + 2 × 2 × \(\sqrt{5}\) + 2² = 5 + 4 \(\sqrt{5}\) + 4 = 9 + 4\(\sqrt{5}\)
\(\frac{1}{x}=\frac{1}{\sqrt{5}+2}=\frac{\sqrt{5}-2}{(\sqrt{5}+2)(\sqrt{5}-2)}=\frac{\sqrt{5}-2}{(\sqrt{5})^{2}-2^{2}}=\frac{\sqrt{5}-2}{5-4}=\sqrt{5}-2\)
\(\frac{1}{x^{2}}\) = (\(\sqrt{5} – 2)^{2}\)
= \((\sqrt{5})^{2}\) – 2 × \(\sqrt{5}\) × 2 + 2² = 5 – 4 \(\sqrt{5}\) + 4 = 9 – 4 \(\sqrt{5}\)
∴ x² + \(\frac{1}{x^{2}}\) = 9 + \(4\sqrt{5}\) + 9 – \(4\sqrt{5}\) = 18
The value of x² + \(\frac{1}{x^{2}}\) = 18

Question 5.
Given \(\sqrt{2}\) = 1.414, find the value of \(\frac{8 – 5\sqrt{2}}{3 – 2\sqrt{2}}\) (to 3 places of decimals).
Solution:

= 4 + \(\sqrt{2}\) = 4 + 1.414 = 5.414

Students can download Maths Chapter 2 Numbers and Sequences Ex 2.5 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.5

Question 1.
Check whether the following sequences are in A.P.?

(i) a – 3, a – 5, a – 7,…
Answer:
a – 3, a – 5, a – 7…….
t₂ – t₁ = a – 5 – (a – 3)
= a – 5 – a + 3
= -2
t₃ – t₂ = a – 7 – (a – 5)
= a – 7 – a + 5
= -2
t₂ – t₁ = t₃ – t₂
(common difference is same)
The sequence is in A.P.

(ii) \(\frac { 1 }{ 2 } \), \(\frac { 1 }{ 3 } \), \(\frac { 1 }{ 4 } \), \(\frac { 1 }{ 5 } \), ……….
Answer:
t₂ – t₁ = \(\frac { 1 }{ 3 } \) – \(\frac { 1 }{ 2 } \) = \(\frac { 2-3 }{ 6 } \) = \(\frac { -1 }{ 6 } \)
t₃ – t₂ = \(\frac { 1 }{ 4 } \) – \(\frac { 1 }{ 3 } \) = \(\frac { 3-4 }{ 12 } \) = \(\frac { -1 }{ 12 } \)
t₂ – t₁ ≠ t₃ – t₂
The sequence is not in A.P.

(iii) 9, 13, 17, 21, 25,…
Answer:
t₂ – t₁ = 13 – 9 = 4
t₃ – t₂ = 17 – 13 = 4
t₄ – t₃ = 21 – 17 = 4
t₅ – t₄ = 25 – 21 = 4
Common difference are equal
∴ The sequence is in A.P.

(iv) \(\frac { -1 }{ 3 } \), 0, \(\frac { 1 }{ 3 } \), \(\frac { 2 }{ 3 } \)
t₂ – t₁ = 0 – (-\(\frac { 1 }{ 3 } \))
= 0 + \(\frac { 1 }{ 3 } \) = \(\frac { 1 }{ 3 } \)
t₃ – t₂ = \(\frac { 1 }{ 3 } \) – 0 = \(\frac { 1 }{ 3 } \)
t₂ – t₁ = t₃ – t₂
The sequence is in A.P.

(v) 1,-1, 1,-1, 1, -1, …
t₂ – t₁ = -1 – 1 = -2
t₃ – t₂ = 1 – (-1) = 1 + 1 = 2
t₄ – t₃ = -1-(1) = – 1 – 1 = – 2
t₅ – t₄ = 1 – (-1) = 1 + 1 = 2
Common difference are not equal
∴ The sequence is not an A.P.

Question 2.
First term a and common difference d are given below. Find the corresponding A.P. ?
(i) a = 5 ,d = 6
Answer:
Here a = 5,d = 6
The general form of the A.P is a, a + d, a + 2d, a + 3d….
The A.P. 5, 11, 17, 23 ….

(ii) a = 7, d = -5
Answer:
The general form of the A.P is a, a + d,
a + 2d, a + 3d… .
The A.P. 7, 2, -3, -8 ….

(iii) a = \(\frac { 3 }{ 4 } \), d = \(\frac { 1 }{ 2 } \)
Answer:
The general form of the A.P is a, a + d, a + 2d, a + 3d….
\(\frac { 3 }{ 4 } \),\(\frac { 3 }{ 4 } \) + \(\frac { 1 }{ 2 } \),\(\frac { 3 }{ 4 } \) + 2(\(\frac { 1 }{ 2 } \)), \(\frac { 3 }{ 4 } \) + 3 (\(\frac { 1 }{ 2 } \))
The A.P. \(\frac { 3 }{ 4 } \), \(\frac { 5 }{ 4 } \), \(\frac { 7 }{ 4 } \), …….

Question 3.
Find the first term and common difference of the Arithmetic Progressions whose n^th terms are given below
(i) t_n = -3 + 2n
(ii) t_n = 4 – 7n
Solution:
(i) a = t₁ = -3 + 2(1) = -3 + 2 = -1
d = t₂ – t₁
Here t₂ = -3 + 2(2) = -3 + 4 = 1
∴ d = t₂ – t₁ = 1 – (-1) = 2
(ii) a = t₁ = 4 – 7(1) = 4 – 7 = -3
d = t₂ – t₁
Here t₂ = 4 – 7(2) = 4 – 14 – 10
∴ d = t₂ – t₁ = 10 – (-3) = -7

Question 4.
Find the 19^th term of an A.P. -11, -15, -19,…
Answer:
First term (a) = -11
Common difference (d) = -15 -(-11)
= -15 + 11 = -4
n = 19
t_n = a + (n – 1) d
t_n = -11 + 18(-4)
= -11 – 72
t₁₉ = -83
19^th term of an A.P. is – 83

Question 5.
Which term of an A.P. 16, 11, 6,1, ……….. is -54?
Solution:
A.P = 16, 11,6, 1, ………..
It is given that
t_n = -54
a = 16, d = t₂ – t₁ = 11 – 16 = -5
∴ t_n = a + (n – 1)d
-54 = 16 + (n – 1) (-5)
-54 = 16 – 5n + 5
21 – 5n = -54
-5n = -54 -21
-5n = -75
n = \(\frac { 75 }{ 5 } \) =15
∴ 15th term is -54.

Question 6.
Find the middle term(s) of an A.P. 9, 15, 21, 27, …, 183.
Answer:
First term (a) = 9
Last term (l) = 183
Common difference (d) = 15 – 9 = 6
n = \(\frac { l-a }{ d } \) + 1
= \(\frac { 183-9 }{ 6 } \) + 1
= \(\frac { 174 }{ 6 } \) + 1
= 29 + 1
= 30
middle term = 15^th term of
16^th term
t_n = a + (n – 1)d
t₁₅ = 9 + 14(6)
= 9 + 84 = 93
t₁₆ = 9 + 15(6)
= 9 + 90 = 99
The middle term is 93 or 99

Question 7.
If nine times ninth term is equal to the fifteen times fifteenth term, show that six times twenty fourth term is zero.
Solution:
Nine times ninth term = Fifteen times fifteenth term
9t₉ = 15t₁₅
9(a + 8d) = 5(a + 14d)
9a + 72d = 15a + 210
15a + 210d – 9a – 72d = 0
⇒ 6a + 138 d = 0
⇒ 6(a + 23 d) = 0
⇒ 6(a + (24 – 1)d) = 0
⇒ 6t₂₄ = 0. Hence it is proved.

Question 8.
If 3 + k, 18 – k, 5k + 1 are in A.P. then find k?
Answer:
3 + k, 18 – k, 5k + 1 are in AP
∴ t₂ – t₁ = t₃ – t₂ (common difference is same)
18 – k – (3 + k) = 5k + 1 – (18 – k)
18 – k – 3 – k = 5k + 1 – 18 + k
15 – 2k = 6k – 17
32 = 8k
k = \(\frac { 32 }{ 8 } \) = 4
The value of k = 4

Question 9.
Find x, y and z, given that the numbers x, 10, y, 24, z are in A.P.
Solution:
A.P = x, 10, y, 24, z,…
d = t₂ – t₁ = 10 – x ………….. (1)
= t₃ – t₂ = y – 10 ………….. (2)
= t₄ – t₃ = 24 – y …………. (3)
= t₅ – t₄ = z – 24 ………….. (4)
(2) and (3)
⇒ y – 10 = 24 – y
2y = 24 + 10 = 34
y = \(\frac { 34 }{ 2 } \) = 17
(1) and (2)
⇒ 10 – x = y – 10
10 – x = 17 – 10 = 7
-x = 7 – 10
-x = -3 ⇒ x = 3
From (3) and (4)
24 – y = z – 24
24 – 17 = z – 24
7 = z – 24
∴ z = 7 + 24 = 31
∴ Solutions x = 3
y = 17
z = 31

Question 10.
In a theatre, there are 20 seats in the front row and 30 rows were allotted. Each successive row contains two additional seats than its front row. How many seats are there in the last row?
Answer:
Number of seats in the first row
(a) = 20
∴ t₁ = 20
Number of seats in the second row
(t₂) = 20 + 2
= 22
Number of seats in the third row
(t₃) = 22 + 2
= 24
Here a = 20 ; d = 2
Number of rows
(n) = 30
t_n = a + (n – 1)d
t₃₀ = 20 + 29(2)
= 20 + 58
t₃₀ = 78
Number of seats in the last row is 78

Question 11.
The sum of three consecutive terms that are in A.P. is 27 and their product is 288. Find the three terms.
Solution:
Let the three consecutive terms be a – d, a, a + d
Their sum = a – d + a + a + d = 27
3a = 27
a = \(\frac{27}{3}\) = 9
Their product = (a – d)(a)(a + d) = 288
= 9(a² – d²) = 288
⇒ 9(9 – d²) = 288
⇒ 9(81 – d²) = 288
81 – d² = 32
-d² = 32 – 81
d² = 49
⇒ d = ± 7
∴ The three terms are if a = 9, d = 7
a – d, a , a + d = 9 – 7, 9 + 7
A.P. = 2, 9, 16
if a = 9, d = -7
A.P. = 9 – (-7), 9, 9 + (-7)
= 16, 9, 2

Question 12.
The ratio of 6^th and 8^th term of an A.P is 7:9. Find the ratio of 9^th term to 13^th term.
Answer:
Given : t₆ : t₈ = 7 : 9 (using t_n = a + (n – 1)d
a + 5d : a + 7d = 7 : 9
9 (a + 5 d) = 7 (a + 7d)
9a + 45 d = 7a + 49d
9a – 7a = 49d – 45d
2a = 4d
a = 2d
To find t₉ : t₁₃
t₉ : t₁₃ = a + 8d : a + 12d
= 2d + 8d : 2d + 12d
= 10d : 14d
= 5 : 7
∴ t₉ : t₁₃ = 5 : 7

Question 13.
In a winter season, the temperature of Ooty from Monday to Friday to be in A.P. The sum of temperatures from Monday to Wednesday is 0° C and the sum of the temperatures from Wednesday to Friday is 18° C. Find the temperature on each of the five days.
Answer:
Let the five days temperature be
(a – 2d), (a – d), a,(a + d) and (a + 2d)
Sum of first three days temperature = 0
a – 2d + a – d + a = 0
3a – 3d = 0
a – d = 0 …..(1)
Sum of the last three days temperature = 18°C
a + a + d + a + 2d = 18
3a + 3d = 18
(÷ by 3) ⇒ a + d = 6 ……(2)
By adding (1) and (2)

Substitute to value of a = 3 in (2)
d = 3
The temperature in 5 days are
(3 – 6), (3 – 3), 3, (3 + 3) and (3 + 6)
-3°C, 0°C, 3°C, 6°C, 9°C

Question 14.
Priya earned ₹15,000 in the first month. Thereafter her salary increases by ₹1500 per year. Her expenses are ₹13,000 during the first year and the expenses increases by ₹900 per year. How long will it take her to save ₹20,000 per month.
Answer:
Tabulate the given table

Monthly savings form an A.P.
2000, 2600, 3200 …..
a = 2000; d = 2600 – 2000 = 600
Given t_n = 20,000
t_n = a + (n – 1) d
20000 = 2000 + (n – 1) 600
20000 = 2000 + 600n – 600
= 1400 + 600n
20000 – 1400 = 600n
18600 = 600n
n = \(\frac { 18600 }{ 600 } \) = 31
He will take 31 years to save ₹ 20,000 per month

Students can download Maths Chapter 2 Real Numbers Ex 2.6 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.6

Question 1.
Simplify the following using addition and subtraction properties of surds:
(i) 5\(\sqrt{3}\) + 18\(\sqrt{3}\) – 2\(\sqrt{3}\)
(ii) 4\(\sqrt[3]{5}\) + 2\(\sqrt[3]{5}\) – 3\(\sqrt[3]{5}\)
(iii) 3\(\sqrt{75}\) + 5\(\sqrt{48}\) – \(\sqrt{243}\)
(iv) 5\(\sqrt[3]{40}\) + 2\(\sqrt[3]{625}\) – 3\(\sqrt[3]{320}\)
Solution:
(i) 5\(\sqrt{3}\) + 18\(\sqrt{3}\) – 2\(\sqrt{3}\) = (5 + 18 – 2)\(\sqrt{3}\)
= (23 – 2) \(\sqrt{3}\) = 21\(\sqrt{3}\)

(ii) 4\(\sqrt[3]{5}\) + 2\(\sqrt[3]{5}\) – 3\(\sqrt[3]{5}\) = (4 + 2 – 3) \(\sqrt[3]{5}\)
= (6 – 3) \(\sqrt[3]{5}\) = 3\(\sqrt[3]{5}\)

(iii) 3\(\sqrt{75}\) + 5\(\sqrt{48}\) – \(\sqrt{243}\) = \(3\sqrt{5^{2}×3} + 5\sqrt{2^{4}×3} – \sqrt{3^{5}}\)

= 3 × 5\(\sqrt{3}\) + 5 × 2²\(\sqrt{3}\) – 3²\(\sqrt{3}\) = 15\(\sqrt{3}\) + 20\(\sqrt{3}\) – 9\(\sqrt{3}\)
= (15 + 20 – 9)\(\sqrt{3}\)
= (35 – 9)\(\sqrt{3}\)
= 26 \(\sqrt{3}\)

(iv) 5\(\sqrt[3]{40}\) + 2\(\sqrt[3]{625}\) – 3\(\sqrt[3]{320}\)

= 5\(\sqrt[3]{2^{3}×5} + 2\sqrt[3]{5^{3}×5} – 3\sqrt[3]{2^{3}×2^{3}×5}\)
5 × 2\(\sqrt[3]{5} + 2 × 5\sqrt[3]{5} – 3 × 2 × 2\sqrt[3]{5} \)
= 10\(\sqrt[3]{5} + 10\sqrt[3]{5} – 12\sqrt[3]{5} \)
= 20\(\sqrt[3]{5} – 12\sqrt[3]{5}\)
= 8\(\sqrt[3]{5}\)

Question 2.
Simplify the following using multiplication and division properties of surds:
(i) \(\sqrt{3}\) × \(\sqrt{5}\) × \(\sqrt{2}\)
(ii) \(\sqrt{35}\) ÷ \(\sqrt{7}\)
(iii) \(\sqrt[3]{27}\) × \(\sqrt[3]{8}\) × \(\sqrt[3]{125}\)
(iv) (7\(\sqrt{a}\) – 5\(\sqrt{b}\)) (7\(\sqrt{a}\) + 5\(\sqrt{b}\))
(v) (\(\sqrt{\frac{225}{729}} – \sqrt{\frac{25}{144}}\)) ÷ \(\sqrt{\frac{16}{81}}\)
Solution:
(i) \(\sqrt{3}\) × \(\sqrt{5}\) × \(\sqrt{2}\) = \(\sqrt{3×5×2} = \sqrt{30}\)

(ii) \(\sqrt{37} ÷ \sqrt{7} = \frac{\sqrt{35}}{\sqrt{7}} = \sqrt{\frac{35}{7}} = \sqrt{5}\)

(iii) \(\sqrt[3]{27}\) × \(\sqrt[3]{8}\) × \(\sqrt[3]{125}\) = \(\sqrt[3]{27×8×125}\)
= \(\sqrt[3]{3^{3}×2^{3}×5^{3}}\) = 3 × 2 × 5 = 30

(iv) (7\(\sqrt{a}\) – 5\(\sqrt{b}\)) (7\(\sqrt{a}\) + 5\(\sqrt{b}\))
[using a2 – b2 = (a + b) (a – b)]
(7\(\sqrt{a}\) – 5\(\sqrt{b}\)) (7\(\sqrt{a}\) + 5\(\sqrt{b}\)) = \((7\sqrt{a})^{2} – (5\sqrt{b})^{2}\) = 49a – 25b

(v) (\(\sqrt{\frac{225}{729}} – \sqrt{\frac{25}{144}}\)) ÷ \(\sqrt{\frac{16}{81}}\)


= \(\frac{5}{36}\) × \(\frac{9}{4}\)
= \(\frac{5×1}{4×4}\)
= \(\frac{5}{16}\)

Question 3.
If \(\sqrt{2}\) = 1.414, \(\sqrt{3}\) = 1.732, \(\sqrt{5}\) = 2.236, \(\sqrt{10}\) = 3.162, then find the values of the following correct to 3 places of decimals.
(i) \(\sqrt{40}\) – \(\sqrt{20}\)
(ii) \(\sqrt{300}\) + \(\sqrt{90}\) – \(\sqrt{8}\)
Solution:
(i) \(\sqrt{40}\) – \(\sqrt{20}\) = \(\sqrt{4×10} – \sqrt{4×5} = 2\sqrt{10} – 2\sqrt{5}\)
= 2 × 3.162 – 2 × 2.236 = 6.324 – 4.472 = 1.852

(ii) \(\sqrt{300}\) + \(\sqrt{90}\) – \(\sqrt{8}\) = \(\sqrt{3×100} + \sqrt{9×10} – \sqrt{4×2}\)
= 10\(\sqrt{3}\) + 3\(\sqrt{10}\) – 2\(\sqrt{2}\)
= 10 × 1.732 + 3 × 3.162 – 2 × 1.414
= 17.32 + 9.486 – 2.828
= 26.806 – 2.828
= 23.978

Question 4.
Arrange surds in descending order
(i) \(\sqrt[3]{5}\), \(\sqrt[9]{4}\), \(\sqrt[6]{3}\)
Solution:
LCM of 3, 9 and 6 is 18

\(\sqrt[3]{5}\) = \(\sqrt[3×6]{5^{6}}\) = \(\sqrt[18]{15625}\)
\(\sqrt[9]{4}\) = \(\sqrt[2×9]{4^{2}}\) = \(\sqrt[18]{16}\)
\(\sqrt[6]{3}\) = \(\sqrt[3×6]{3^{3}}\) = \(\sqrt[18]{27}\)
\(\sqrt[18]{15625}\) > \(\sqrt[18]{27}\) > \(\sqrt[18]{16}\)
\(\sqrt[3]{5}\) > \(\sqrt[6]{3}\) > \(\sqrt[9]{4}\)

(ii) \(\sqrt[2]{\sqrt[3]{5}}\), \(\sqrt[3]{\sqrt[4]{7}}\), \(\sqrt{\sqrt{3}}\)
Solution:
\(\sqrt[2]{\sqrt[3]{5}}\) = \(\sqrt[6]{5}\); \(\sqrt[3]{\sqrt[4]{7}}\) = \(\sqrt[12]{7}\); \(\sqrt{\sqrt{3}}\) = \(\sqrt[4]{3}\)
LCM of 6, 12 and 4 is 12

\(\sqrt[2]{\sqrt[3]{5}}\) = \(\sqrt[6]{5}\) = \(\sqrt[12]{5^{2}}\) = \(\sqrt[12]{25}\)
\(\sqrt[3]{\sqrt[4]{7}}\) = \(\sqrt[12]{7}\) = \(\sqrt[12]{7}\)
\(\sqrt{\sqrt{3}}\) = \(\sqrt[4]{3}\) = \(\sqrt[12]{3^{3}}\) = \(\sqrt[12]{27}\)
\(\sqrt[12]{27}\) > \(\sqrt[12]{25}\) > \(\sqrt[12]{7}\)
\(\sqrt{\sqrt{3}}\) > \(\sqrt[2]{\sqrt[3]{5}}\) > \(\sqrt[3]{\sqrt[4]{7}}\)

Question 5.
Can you get a pure surd when you find:
(i) the sum of two surds
(ii) the difference of two surds
(iii) the product of two surds
(iv) the quotient of two surds
Justify each answer with an example.
Solution:
(i) Yes we can get a surd.
Example:
(a) 3\(\sqrt{2}\) + 5\(\sqrt{2}\) = (3 + 5)\(\sqrt{2}\) = 8\(\sqrt{2}\)
(b) 3\(\sqrt{6}\) + 2\(\sqrt{6}\) = (3 + 2)\(\sqrt{6}\) = 5\(\sqrt{6}\)

(ii) Yes we can get a surd.
Example:
(a) \(\sqrt{75}\) – \(\sqrt{48}\) = \(\sqrt{25×3}\) – \(\sqrt{16×3}\) = (5 – 4) \(\sqrt{3}\) = \(\sqrt{3}\)
(b) \(\sqrt{98}\) – \(\sqrt{72}\) = \(\sqrt{49×2}\) – \(\sqrt{36×2}\) = (7 – 6) \(\sqrt{2}\) = \(\sqrt{2}\)

(iii) Yes we can get a surd.
Example:
(a) \(\sqrt{8}\) × \(\sqrt{6}\) = \(\sqrt{8×6}\) = \(\sqrt{48}\)
(b) \(\sqrt{11}\) × \(\sqrt{3}\) = \(\sqrt{11×3}\) = \(\sqrt{33}\)

(iv) Yes we can get a surd.
Example:
(a) \(\sqrt{55}\) ÷ \(\sqrt{5}\) = \(\frac{\sqrt{11×5}}{\sqrt{5}} = \sqrt{11}\)
(b) \(\sqrt{65}\) ÷ \(\sqrt{5}\) = \(\frac{\sqrt{13×5}}{\sqrt{13}} = \sqrt{5}\)

Question 6.
Can you get a rational number when you compute:
(i) the sum of two surds
(ii) the difference of two surds
(iii) the product of two surds
(iv) the quotient of two surds
Justify each answer with an example.
Solution:
(i) Yes, the sum of two surds will give a rational number.
Example:
(a) (2 + \(\sqrt{3}\)) + (2 – \(\sqrt{3}\)) = 4
(b) (\(\sqrt{5}\) + 4) + (7 – \(\sqrt{5}\)) = 11

(ii) Yes, the difference of two surds will give a rational number.
Example:
(a) (5 + \(\sqrt{7}\)) – (- 5 + \(\sqrt{7}\)) = 10
(b) (\(\sqrt{11}\) + 5) – (-3 + \(\sqrt{11}\)) = 8

(iii) Yes, the product of two surds will give a rational number.
Example:
(a) \(\sqrt{125}\) × \(\sqrt{45}\) = \(\sqrt{25×5}\) × \(\sqrt{9×5}\) = 5\(\sqrt{5}\) × 3\(\sqrt{5}\) = 15 × 5 = 75
(b) \(\sqrt{150}\) × \(\sqrt{6}\) = \(\sqrt{25×6}\) × \(\sqrt{6}\) = 5\(\sqrt{6}\) × \(\sqrt{6}\) = 5 × 6 = 30

(iv) Yes. The quotient of two surds will give a rational number.
Example:
(a) \(\sqrt{32}\) ÷ \(\sqrt{8}\) = \(\frac{\sqrt{8×4}}{\sqrt{8}} = \sqrt{4}\) = 2
(b) \(\sqrt{50}\) ÷ \(\sqrt{2}\) = \(\frac{\sqrt{25×2}}{\sqrt{2}} = \sqrt{25}\) = 5

Students can download Maths Chapter 3 Algebra Ex 3.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.1

Question 1.
Which of the following expressions are polynomials. If not give reason:
(i) \(\frac{1}{x^2}\) + 3x – 4
Solution:
(i) \(\frac{1}{x^2}\) + 3x – 4 is not a polynomial. Since the exponent of x² is not a whole number, but it is (\(\frac{1}{x^2}\) = x^-2) negative number.

(ii) x² (x – 1)
Solution:
x² (x – 1) is a polynomial.

(iii) \(\frac{1}{x}\) (x + 5)
Solution:
\(\frac{1}{x}\) (x + 5) is not a polynomial. Since the exponent of x is not a whole number, but it is (\(\frac{1}{x}\) = x^-1) negative number.

(iv) \(\frac{1}{x^{-2}}\) + \(\frac{1}{x^{-1}}\) + 7
Solution:
\(\frac{1}{x^{-2}}\) + \(\frac{1}{x^{-1}}\) + 7 is a polynomial. (\(\frac{1}{x^{-2}}\) = x² and \(\frac{1}{x^{-1}}\) = x)

(v) √5x² + √3x + √2
Solution:
√5x² + √3x + √2 is a polynomial.

(vi) m² – \(\sqrt[3]{m}\) + 7m – 10
m² –\(\sqrt[3]{m}\) + 7m – 10 is not a polynomial. Since the exponent of m is not a whole number.
(\(\sqrt[3]{m}\) = m^1/3)

Question 2.
Write the coefficient of x² and x in each of the following polynomials.
(i) 4 + \(\frac{2}{5}\) x² – 3x
Solution:
Coefficient of x² is \(\frac{2}{5}\) and coefficient of x is -3.

(ii) 6 – 2x² + 3x³ – √7x
Solution:
Coefficient of x² is -2 and coefficient of x is -√7

(iii) π x² – x + 2
Solution:
Coefficient of x² is π and coefficient of x is -1.

(iv) √3x² + √2x + 0.5
Solution:
Coefficient of x² is √3 and coefficient of x is √2

(v) x² – \(\frac{7}{2}\) x + 8
Solution:
Coefficient of x² is 1 and coefficient of x is –\(\frac{7}{2}\)

Question 3.
Find the degree of the following polynomials.
(i) 1 – √2 y² + y⁷
(ii) \(\frac{x^{3}-x^{4}+6 x^{6}}{x^{2}}\)
(iii) x³ (x² + x)
(iv) 3x⁴ + 9x² + 27x⁶
(v) 2√5p⁴ \(-\frac{8 p^{3}}{\sqrt{3}}+\frac{2 p^{2}}{7}\)
Solution:
(i) 1 – √2 y² + y⁷
The degree of the polynomial is 7.

(ii)
= x – x² + 6x⁴
The degree of the polynomial is 4.

(iii) x³ (x² + x) = x⁵ + x⁴
The degree of the polynomial is 5.

(iv) 3x⁴ + 9x² + 27x⁶
The degree of the polynomial is 6.

(v) 2√5p⁴ \(-\frac{8 p^{3}}{\sqrt{3}}+\frac{2 p^{2}}{7}\)
The degree of the polynomial is 4.

Question 4.
Rewrite the following polynomial in standard form.
(i) x – 9 + √7x³ + 6x²
Solution:
The standard form is √7x³ + 6x² – x – 9
(or) – 9 + x + 6x² + √7x³

(ii) √2x² – \(\frac{7}{2}\) x⁴ + x – 5x³
Solution:
The standard form is – \(\frac{7}{2}\) x⁴ – 5x³ + √2x² + x
(or) x + √2x² – 5x³ – \(\frac{7}{2}\) x⁴

(iii) 7x³ – \(\frac{6}{5}\) x² + 4x – 1
Solution:
The given polynomial is in standard form (or) – 1 + 4x – \(\frac{6}{5}\) x² + 7x³

(iv) y² + √5y³ – 11 – \(\frac{7}{3}\) y + 9y⁴
Solution:
The standard form is 9y⁴ + √5y³ + y² – \(\frac{7}{3}\) y – 11
(or) – 11 – \(\frac{7}{3}\) y + y² + √5y³ + 9y⁴

Question 5.
Add the following polynomials and find the degree of the resultant polynomial
(i) p(x) = 6x² – 7x + 2; q(x) = 6x³ – 7x + 15
Solution:
p(x) + q(x) = 6x² – 7x + 2 + 6x³ – 7x + 15
= 6x³ + 6x² – 7x – 7x + 2 + 15
= 6x³ + 6x² – 14x + 17
The degree of the polynomial is 3.

(ii) h(x) = 7x³ – 6x + 1; f(x) = 7x² + 17x – 9
Solution:
h(x) + f(x) = 7x³ – 6x + 1 + 7x² + 17x – 9
= 7x³ + 7x² + 11x – 8
The degree of the polynomial is 3.

(iii) f(x) = 16x⁴ – 5x² + 9; g(x) = -6x³ + 7x – 15
Solution:
f(x) + g(x) = 16x⁴ – 5x² + 9 – 6x³ + 7x – 15
= 16x⁴ – 6x³ – 5x² + 7x + 9 – 15
= 16x⁴ – 6x³ – 5x² + 7x – 6
The degree of the polynomial is 4.

Question 6.
Subtract the second polynomial from the first polynomial and find the degree of the resultant polynomial.
(i) p(x) = 7x² + 6x – 1; q(x) = 6x – 9
Solution:
p(x) – q(x) = 7x² + 6x – 1 – (6x – 9)
= 7x² + 6x – 1 – 6x + 9
= 7x² + 6x – 6x – 1 + 9
= 7x² + 8
The degree of the polynomial is 2.

(ii) f(y) = 6y² – 7y + 2; g(y) = 7y + y³
Solution:
f(y) – g(y) = 6y² – 7y + 2 – (7y + y³)
= 6y² – 7y + 2 – 7y – y³
= -y³ + 6y² – 7y – 7y + 2
= -y³ + 6y² – 14y + 2
The degree of the polynomial is 3.

(iii) h(z) = z⁵ – 6z⁴ + z; f(z) = 6z² + 10z – 7
Solution:
h(z) – f(z) = z⁵ – 6z⁴ + z – (6z² + 10z – 7)
= z⁵ – 6z⁴ + z – 6z² – 10z + 7
= z⁵ – 6z⁴ – 6z² + z – 10z + 7
= z⁵ – 6z⁴ – 6z² – 9z + 7
The degree of the polynomial is 5.

Question 7.
What should be added to 2x³ + 6x² – 5x + 8 to get 3x³ – 2x² + 6x + 15?
Solution:
3x³ – 2x² + 6x + 15 – (2x³ + 6x² – 5x + 8)
= 3x³ – 2x² + 6x + 15 – 2x³ – 6x² + 5x – 8
= 3x³ – 2x³- 2x² – 6x² + 6x + 5x + 15 – 8
= x³ – 8x² + 11x + 7
x³ – 8x² + 11x + 7 must be added to get 3x³ – 2x² + 6x + 15.

Question 8.
What must be subtracted from 2x⁴ + 4x² – 3x + 7 to get 3x³ – x² + 2x + 1?
Solution:
2x⁴ + 4x² – 3x + 7 – (3x³ – x² + 2x + 1)
= 2x⁴ + 4x² – 3x + 7 – 3x³ + x² – 2x – 1
= 2x⁴ – 3x³ + 4x² + x² – 3x – 2x + 7 – 1
= 2x⁴ – 3x³ + 5x² – 5x + 6
2x⁴ – 3x³ + 5x² – 5x + 6 must be subtracted to get 3x³ – x² + 2x + 1.

Question 9.
Multiply the following polynomials and find the degree of the resultant polynomial:
(i) p(x) = x² – 9, q(x) = 6x² + 7x – 2
Solution:
p(x) × q(x) = (x² – 9) (6x² + 7x – 2)
= 6x⁴ + 7x³ – 2x² – 54x² – 63x + 18
= 6x⁴ + 7x³ – 56x² – 63x + 18
The degree of the polynomial is 4.

(ii) f(x) = 7x + 2, g(x) = 15x – 9
Solution:
f(x) × g(x) = (7x + 2) (15x – 9)
= 105x² – 63x + 30x – 18
= 105x² – 33x – 18
The degree of the polynomial is 2.

(iii) h(x) = 6x² – 7x + 1, f(x) = 5x – 7
Solution:
h(x) × f(x) = (6x² – 7x + 1) (5x – 7)
= 30x³ – 42x² – 35x² + 49x + 5x – 7
= 30x³ – 77x² + 54x – 7
The degree of the polynomial is 3.

Question 10.
The cost of a chocolate is Rs. (x + y) and Amir bought (x + y) chocolates. Find the total amount paid by him in terms of x and y. If x = 10, y = 5 find the amount paid by him.
Solution:
The cost of a chocolate = (x + y)
Number of chocolates bought by Amir = x + y
Total amount paid by him = (x + y) (x + y)
= x² + xy + xy + y²
= x² + 2xy + y²
When x = 10 and y = 5
The total amount paid by him = (10)² + 2(10)(5) + (5)²
= 100 + 100 + 25 = 225

Question 11.
The length of a rectangle is (3x + 2) units and it’s breadth is (3x – 2) units. Find its area in terms of x. What will be the area if x = 20 units.
Solution:
Length of the rectangle = 3x + 2 units
Breadth of the rectangle = 3x – 2 units
Area of the rectangle = (3x + 2) (3x – 2)
= 9x² – 6x + 6x – 4
= 9x² – 4
When x = 20
Area of the rectangle = 9(20)² – 4
= 9(400) – 4
= 3600 – 4
= 3596 sq.units.

Question 12.
p(x) is a polynomial of degree 1 and q(x) is a polynomial of degree 2. What kind of the polynomial is p(x) × q(x)?
Solution:
Degree of the polynomial p(x) = 1
Degree of the polynomial q(x) = 2
Degree of p(x) × q(x) = 3
The polynomial is a cubic polynomial (or) Polynomial of degree 3.

Students can download Maths Chapter 2 Numbers and Sequences Ex 2.8 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.8

Question 1.
Find the sum of first n terms of the G.P.
(i) 5, -3, \(\frac { 9 }{ 5 } \),-\(\frac { 27 }{ 25 } \), ……
(ii) 256,64,16,…….
Answer:
(i) 5,-3,\(\frac { 9 }{ 5 } \),\(\frac { 27 }{ 55 } \), ….. n terms

(ii) 256,64,16,…….
Answer:
Here a = 256, r = \(\frac { 64 }{ 256 } \) = \(\frac { 1 }{ 4 } \)

Question 2.
Find the sum of first six terms of the G.P. 5,15,45,…
Answer:
Here a = 5, r = \(\frac { 15 }{ 3 } \) = 3, n = 6

Sum of first 6 terms = 1820

Question 3.
Find the first term of the G.P. whose common ratio 5 and whose sum to first 6 terms is 46872.
Answer:
Common ratio (r) = 5
S₆ = 46872

The first term of the G.P. is 12.

Question 4.
Find the sum to infinity of (i) 9 + 3 + 1 + ….(ii) 21 + 14 + \(\frac { 28 }{ 3 } \) ……
Answer:
(i) 9 + 3 + 1 + ….
a = 9, r = \(\frac { 3 }{ 9 } \) = \(\frac { 1 }{ 3 } \)
Sum of infinity term = \(\frac { a }{ 1 – r } \) = \(\frac{9}{1-\frac{1}{3}}\)

Question 5.
If the first term of an infinite G.P. is 8 and its sum to infinity is \(\frac { 32 }{ 3 } \) then find the common ratio.
Answer:
Here a = 8, S∞ = \(\frac { 32 }{ 3 } \)
\(\frac { a }{ 1-r } \) = \(\frac { 32 }{ 3 } \)
\(\frac { 8 }{ 1-r } \) = \(\frac { 32 }{ 3 } \)
32 – 32 r = 24 ⇒ 32 r = 8
r = \(\frac { 8 }{ 32 } \) = \(\frac { 1 }{ 4 } \)
Common ration = \(\frac { 1 }{ 4 } \)

Question 6.
Find the sum to n terms of the series
(i) 0.4 + 0.44 + 0.444 + …… to n terms
Answer:


(ii) 3 + 33 + 333 + ………… to n terms
Answer:
S_n = 3 + 33 + 333 + …. to n terms
= 3[1 + 11 + 111 + …. to n terms]
= \(\frac { 3 }{ 9 } \) [9 + 99 + 999 + …. n terms]
= \(\frac { 1 }{ 3 } \) [(10 – 1) + (100 – 1) + (1000 – 1) + …… n terms]
= \(\frac { 1 }{ 3 } \) [10 + 100 + 1000 + ….. n terms – (1 + 1 + 1 ….. n terms)]

Question 7.
Find the sum of the Geometric series 3 + 6 + 12 + …….. + 1536
Answer:
3 + 6 + 12 …. +1536
a = 3, r = \(\frac { 6 }{ 3 } \) = 2
t_n = 1536


∴ Sum of the series is 3069

Question 8.
Kumar writes a letter to four of his friends. He asks each one of them to copy the letter and mail to four different persons with the instruction that they continue the process similarly. Assuming that the process is unaltered and it costs ₹2 to mail ong letter, find the amount spent on postage when 8th set of letters is mailed.
Answer:
When kumar writes a letter to his friend.Friend writes a letter to another person.
It form a G.P
The G.P is 4, 16, 64,………
Here a = 4, r = 4
The last term is 4 (4)^8-1 = 4(4)⁷

Question 9.
Find the rational form of the number 0.123 .
Answer:
Let x = \(\overline { 0.123 } \)
= 0.123123123….
= 0.123 + 0.000123 + 000000123 + ….
This is an infinite G.P

Question 10.
If S_n = (x + y) + (x² + xy + y²) + (x³ + x²y + xy² + y³) + ………… n terms then prove that
Answer:
S_n = (x + y) + (x² + xy + y²) + (x³ + x²y + xy² + y³) + …….. n
Multiply by x
x S_n = x(x + y) + x(x² + xy + y²) + x(x³ + x²y + xy² + y³) + ……….. n
= x² + xy + x³ + x²y + xy² + x⁴ + x³y + x²y² + xy³ + …… n terms ……(1)
Multiply by y
yS_n = y(x + y) + y(x² + xy + y²) + y(x³ + x²y + xy² + y³) + ….. n
= xy + y² + x²y + xy² + y³ + x³y + x²y² + xy³ + y⁴ + ….. n terms
Subtract (1) and (2)
x S_n – y S_n = x² + xy + x³ + x²y + xy² + x⁴ + x³y + x²y² + xy³ + …….
– xy + y² + x²y + xy² + y³ + x³y + x²y² + xy³ + y⁴ + ……
(x – y) S_n = (x² + x³ + x⁴ + ……) – (y² + y³ + y⁴ + ……)
[ a = x²; r = x and a = y²; r = y, S_n = \(\frac{a\left(r^{n}-1\right)}{r-1}\)]

Hence it is proved.

Students can download Maths Chapter 2 Real Numbers Ex 2.9 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.9

Question 1.
If n is a natural number then √n is……….
(a) always a natural number
(b) always an irrational number
(c) always a rational number
(d) may be rational or irrational
Solution:
(d) may be rational or irrational

Question 2.
Which of the following is not true?
(a) Every rational number is a real number
(b) Every integer is a rational number
(c) Every real number is an irrational number
(d) Every natural number is a whole number
Solution:
(c) Every real number is an irrational number

Question 3.
Which one of the following, regarding sum of two irrational numbers, is true?
(a) always an irrational number
(b) may be a rational or irrational number
(c) always a rational number
(d) always an integer
Solution:
(b) may be a rational or irrational number

Question 4.
Which one of the following has a terminating decimal expansion?
(a) \(\frac{5}{64}\)
(b) \(\frac{8}{9}\)
(c) \(\frac{14}{15}\)
(d) \(\frac{1}{12}\)
Solution:
(a) \(\frac{5}{64}\)
Hint:
\(\frac{5}{64}\) = \(\frac{5}{2^{6}}\)

Question 5.
Which one of the following is an irrational number?
(a) \(\sqrt{25}\)
(b) \(\sqrt{\frac{9}{4}}\)
(c) \(\frac{7}{11}\)
(d) π
Solution:
(d) π
Hint:
We take frequently π as \(\frac{22}{7}\) (which gives the value of 3.1428571428571…….) to be its correct value, but in reality these are only approximations

Question 6.
An irrational number between 2 and 2.5 is………
(a) \(\sqrt{11}\)
(b) √5
(c) \(\sqrt{2.5}\)
(d) √8
Solution:
(b) √5
Hint:
√5 = 2.236, it lies between 2 and 2.5

Question 7.
The smallest rational number by which \(\frac{1}{3}\) should be multiplied so that its decimal expansion terminates with one place of decimal is ………
(a) \(\frac{1}{10}\)
(b) \(\frac{3}{10}\)
(c) 3
(d) 30
Solution:
(b) \(\frac{3}{10}\)
Hint:
\(\frac{1}{3}\) × \(\frac{3}{10}\) = \(\frac{1}{10}\) = \(\frac{1}{2×5}\) it has terminating decimal expansion.

Question 8.
If \(\frac{1}{7}\) = 0.\(\overline { 142857 }\) then the value of \(\frac{5}{7}\) is ………..
(a) 0.\(\overline { 142857 }\)
(b) 0.\(\overline { 714285 }\)
(c) 0.\(\overline { 571428 }\)
(d) 0.714285
Solution:
(b) 0.\(\overline { 714285 }\)

Question 9.
Find the odd one out of the following.
(a) \(\sqrt{32}×\sqrt{2}\)
(b) \(\frac{\sqrt{27}}{\sqrt{3}}\)
(c) \(\sqrt{72}×\sqrt{8}\)
(d) \(\frac{\sqrt{54}}{\sqrt{18}}\)
Solution:
(b) \(\frac{\sqrt{27}}{\sqrt{3}}\)
Hint:
\(\frac{\sqrt{27}}{\sqrt{3}}\) = \(\frac{\sqrt{27}}{\sqrt{3}}\) = √9 = 3. It is an odd number

Question 10.
0.\(\overline { 34 }\) + 0.3\(\overline { 4 }\) = ……….
(a) 0.6\(\overline { 87 }\)
(b) 0.\(\overline { 68 }\)
(c) 0.6\(\overline { 8 }\)
(d) 0.68\(\overline { 7 }\)
Solution:
(a) 0.6\(\overline { 87 }\)
Hint:
0.34343434
0.34444444
0.68787878

Question 11.
Which of the following statement is false?
(a) The square root of 25 is 5 or -5
(b) \(-\sqrt{25}\) = -5
(c) \(\sqrt{25}\) = 5
(d) \(\sqrt{25}\) = ±5
Solution:
(d) \(\sqrt{25}\) = ±5

Question 12.
Which one of the following is not a rational number?
(a) \(\sqrt{\frac{8}{18}}\)
(b) \(\frac{7}{3}\)
(c) \(\sqrt{0.01}\)
(d) \(\sqrt{13}\)
Solution:
(d) \(\sqrt{13}\)

Question 13.
\(\sqrt{27}\) + \(\sqrt{12}\) = ……….
(a) \(\sqrt{39}\)
(b) 5√6
(c) 5√3
(d) 3√5
Solution:
(d) 3√5
Hint:
\(\sqrt{27}\) + \(\sqrt{12}\) = \(\sqrt{9×3}\) + \(\sqrt{3×4}\) = 3√3 + 2√3 = 5√3

Question 14.
If \(\sqrt{80}\) = k√5, then k = ………
(a) 2
(b) 4
(c) 8
(d) 16
Solution:
(b) 4
Hint:
\(\sqrt{80}\) = k√5
\(\sqrt{16×5}\) = k√5
4√5 = k√5
∴ k = 4

Question 15.
4√7 × 2√3 = ……….
(a) 6\(\sqrt{10}\)
(b) 8\(\sqrt{21}\)
(c) 8\(\sqrt{10}\)
(d) 6\(\sqrt{21}\)
Solution:
(b) 8\(\sqrt{21}\)
Hint:
4√7 × 2√3 = 4 × 2\(\sqrt{7×3}\) = 8\(\sqrt{21}\)

Question 16.
When written with a rational denominator, the expression \(\frac {2\sqrt{3}}{3\sqrt{2}}\) can be simplified as……..
(a) \(\frac {\sqrt{2}}{3}\)
(b) \(\frac {\sqrt{3}}{2}\)
(c) \(\frac {\sqrt{6}}{3}\)
(d) \(\frac {2}{3}\)
Solution:
(c) \(\frac {\sqrt{6}}{3}\)

Question 17.
When (2√5 – √2)² is simplified, we get………
(a) 4√5 + 2√2
(b) 22 – 4\(\sqrt{10}\)
(c) 8 – 4\(\sqrt{10}\)
(d) 2\(\sqrt{10}\) – 2
Solution:
(b) 22 – 4\(\sqrt{10}\)
Hint:
(2√5 – √2)² = (2√5)² + (√2)² – 2 × 2√5 × √2
= 20 – 4\(\sqrt{10}\) + 2
= 22 – 4\(\sqrt{10}\)

Question 18.
\((0.000729)^\frac{-3}{4}\) × \((0.09)^\frac{-3}{4}\) = ……..
(a) \(\frac {10^3}{3^3}\)
(b) \(\frac {10^5}{3^5}\)
(c) \(\frac {10^2}{3^2}\)
(d) \(\frac {10^6}{3^6}\)
Solution:
(d) \(\frac {10^6}{3^6}\)
Hint:

Question 19.
If √9^x = \(\sqrt[3]{9^2}\), then x = …….
(a) \(\frac {2}{3}\)
(b) \(\frac {4}{3}\)
(c) \(\frac {1}{3}\)
(d) \(\frac {5}{3}\)
Solution:
(b) \(\frac {4}{3}\)
Hint:

Question 20.
The length and breadth of a rectangular plot are 5 × 10⁵ and 4 × 10⁴ metres respectively. Its area is ……….
(a) 9 × 10¹ m²
(b) 9 × 10⁹ m²
(c) 2 × 10¹⁰ m²
(d) 20 × 10²⁰ m²
Solution:
(c) 2 × 10¹⁰ m²
Hint:
Area of a rectangle = l × b = 5 × 10⁵ × 4 × 10⁴
= 5 × 4 × 10⁵⁺⁴
= 20 × 10⁹
= 2.0 × 10 × 10⁹
= 2 × 10¹⁰ m²

Students can download Maths Chapter 1 Relations and Functions Ex 1.5 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Ex 1.5

Question 1.
Using the functions f and g given below, find fog and gof Check whether fog = gof.

(i) f(x) = x – 6, g(x) = x²
Answer:
f(x) = x – 6, g(x) = x²
fog = fog (x)
= f(g(x))
fog = f(x)²
= x² – 6
gof = go f(x)
= g(x – 6)
= (x – 6)²
= x² – 12x + 36
fog ≠ gof

(ii) f(x) = \(\frac { 2 }{ x } \), g(x) = 2x² – 1
Answer:
f(x) – \(\frac { 2 }{ x } \); g(x) = 2x² – 1
fag = f[g (x)]
= f(2x² – 1)
= \(\frac{2}{2 x^{2}-1}\)
gof = g [f(x)]
= g (\(\frac { 2 }{ x } \))
= 2 (\(\frac { 2 }{ x } \))² – 1
\(=2 \times \frac{4}{x^{2}}-1\)
\(=\frac{8}{x^{2}}-1\)
fog ≠ gof

(iii) f(x) = \(\frac { x+6 }{ 3 } \), g(x) = 3 – x
Answer:
f(x) = \(\frac { x+6 }{ x } \), g(x) = 3 – x
fog = f[g(x)]
= f(3 – x)

(iv) f(x) = 3 + x, g(x) = x – 4
Answer:
f(x) = 3 + x ;g(x) = x – 4
fog = f[g(x)]
= f(x – 4)
= 3 + x – 4
= x – 1
gof = g[f(x)]
= g(3 + x)
= 3 + x – 4
= x – 1
fog = gof

(v) f(x) = 4x² – 1,g(x) = 1 + x
Answer:
f(x) = 4x² – 1 ; g(x) = 1 + x
fog = f[g(x)]
= 4(1 + x)
= 4(1 + x)² – 1
= 4[1 + x² + 2x] – 1
= 4 + 4x² + 8x – 1
= 4x² + 8x + 3
gof = g [f(x)]
= g (4x² – 1)
= 1 + 4x² – 1
= 4x²
fog ≠ gof

Question 2.
Find the value of k, such that fog = gof
(i) f(x) = 3x + 2, g(x) = 6x – k
(ii) f(x) = 2x – k, g(x) = 4x + 5
Solution:
(i) f(x) = 3x + 2, g(x) = 6x – k
fog(x) = f(g(x)) = f(6x – k) = 3(6x – k) + 2
= 18x – 3k + 2 …………… (1)
gof(x) = g(f(x)) = g(3x + 2) = 6(3x + 2) – k
= 18x + 12 – k ……………. (2)
(1) = (2)
⇒ 18x – 3k + 2 = 18x + 12 – k
2k = -10
k = -5

(ii) f(x) = 2x – k, g(x) = 4x + 5
fog(x) = f(g(x)) = f(4x + 5) = 2(4x + 5) – k
= 8x + 10 – k ……………… (1)
gof(x) = g(f(x)) = g(2x – k) = 4(2x – k) + 5
= 8x – 4k + 5 ……………. (2)
(1) = (2)
⇒ 8x + 10 – k = 8x – 4k + 5
3k = -5
k = \(\frac{-5}{3}\)

Question 3.
If f(x) = 2x – 1, g(x) = \(\frac { x+1 }{ 2 } \), show that f o g = g o f = x
Answer:
f(x) = 2x – 1 ; g(x) = \(\frac { x+1 }{ 2 } \)
fog = f[g(x)]

∴ fog = gof = x
Hence it is proved.

Question 4.
(i) If f (x) = x² – 1, g(x) = x – 2 find a, if gof(a) = 1.
(ii) Find k, if f(k) = 2k – 1 and fof (k) = 5.
Solution:
(i) f(x) = x² – 1, g(x) = x – 2
Given gof(a) = 1
gof(x) = g(f(x)
= g(x² – 1) = x² – 1 – 2
= x² – 3
gof(a) ⇒ a² – 3 = 1 =+ a² = 4
a = ± 2
(ii) f(k) = 2k – 1
fo f(k) = 5
f(f(k)m = f(2k – 1) = 5
⇒ 2(2k – 1) – 1 = 5
4 k – 2 – 1 = 5 ⇒ 4k = 8
k = 2

Question 5.
Let A,B,C ⊂ N and a function f: A → B be defined by f(x) = 2x + 1 and g: B → C be defined by g(x) = x² . Find the range of fog and gof.
Answer:
f(x) = 2x + 1 ; g(x) = x²
fog = f[g(x)]
= f(x²)
= 2x² + 1
2x² + 1 ∈ N
g o f = g [f(x)]
= g (2x + 1)
g o f = (2x + 1)²
(2x + 1)² ∈ N
Range = {y/y = 2x² + 1, x ∈ N};
{y/y = (2x + 1)², x ∈ N)

Question 6.
If f(x) = x² – 1. Find (i)f(x) = x² – 1, (ii)fofof
Solution:
(i) f(x) = x² – 1
fof(x) = f(fx)) = f(x² – 1)
= (x² – 1 )² – 1;
= x⁴ – 2x² + 1 – 1
= x⁴ – 2x²
(ii) fofof = f o f(f(x))
= f o f (x⁴ – 2x²)
= f(f(x⁴ – 2x²))
= (x⁴ – 2x²)² – 1
= x⁸ – 4x⁶ + 4x⁴ – 1

Question 7.
If f : R → R and g : R → R are defined by f(x) = x⁵ and g(x) = x⁴ then check if f, g are one – one and fog is one – one?
Answer:
f(x) = x⁵ – It is one – one function
g(x) = x⁴ – It is one – one function
fog = f[g(x)]
= f(x⁴)
= (x⁴)⁵
fag = x²⁰
It is also one-one function.

Question 8.
Consider the functions f(x), g(x), h(x) as given below. Show that (fog)oh = fo(goh) in each case.
(i) f(x) = x – 1, g(x) = 3x + 1 and h(x) = x²
(ii) f(x) = x², g(x) = 2x and h(x) = x + 4
(iii) f(x) = x – 4, g(x) = x² and h(x) = 3x – 5
Solution:
(i) f(x) = x – 1, g(x) = 3x + 1 and h(x) = x²
f(x) = x – 1
g(x) = 3x + 1
f(x) = x²
(fog)oh = fo(goh)
LHS = (fog)oh
fog = f(g(x)) = f(3x + 1) = 3x + 1 – 1 = 3x
(fog)oh = (fog)(h(x)) = (fog)(x² ) = 3²  ……………. (1)
RHS = fo(goh)
goh = g(h(x)) = g(x²) = 3x² + 1
fo(goh) = f(3x² + 1) = 3x² + 1 – 1= 3x² ………… (2)
LHS = RHS Hence it is verified.

(ii) f(x) = x², g(x) = 2x, h(x) = x + 4
(fog)oh = fo(goh)
LHS = (fog)oh
fog = f(g(x)) = f(2x) = (2x)² = 4x²
(fog)oh = (fog) h(x) = (fog) (x + 4)
= 4(x + 4)² = 4(x² + 8x+16)
= 4x² + 32x + 64 ………….. (1)
RHS = fo(goh) goh = g(h(x)) = g(x + 4)
= 2(x + 4) = (2x + 8)
fo(goh) = f(goh) = f(2x + 8) = (2x + 8)²
= 4x² + 32x + 64 ……………… (2)
(1) = (2)
LHS = RHS
∴ (fog)oh = fo(goh) It is proved.

(iii) f(x) = x – 4, g(x) = x², h(x) = 3x – 5
(fog)oh = fo(goh)
LHS = (fog)oh
fog = f(g(x)) = f(x²) = x² – 4
(fog)oh = (fog)(3x – 5) = (3x – 5)² – 4
= 9x² – 30x + 25 -4
= 9x² – 30x + 21 ………….. (1)
∴ RHS = fo(goh)
(goh) = g(h(x)) = g(3x – 5) = (3x – 5)²
= 9x² – 30x + 25
fo(goh) = f(9x² – 30 x + 25)
= 9x² – 30x + 25 – 4
= 9x² – 30x + 21 …………… (2)
(1) = (2)
LHS = RHS
∴ (fog)oh = fo(goh)
It is proved.

Question 9.
Let f = {(-1, 3), (0, -1), (2, -9)} be a linear function from Z into Z. Find f(x).
Answer:
The linear equation is f(x) = ax + b
f(-1) = 3
a(-1) + b = 3
-a + b = 3 ….(1)
f(0) = -1
a(0) + b = -1
0 + b = -1
b = -1
Substitute the value of b = -1 in (1)
-a – 1 = 3
-a = 3 + 1
-a = 4
a = -4
∴ The linear equation is -4(x) -1 = -4x – 1 (or) – (4x + 1)

Question 10.
In electrical circuit theory, a circuit C(t) is called a linear circuit if it satisfies the superposition principle given by C(at₁ + bt₂) = aC(t₁) + bC(t₂), where a,b are constants. Show that the circuit C(t) = 31 is linear.
Solution:
Given C(t) = 3t. To prove that the function is linear
C(at₁) = 3a(t₁)
C(bt₂) = 3 b(t₂)
C(at₁ + bt₂) = 3 [at₁ + bt₂] = 3at₁ + 3bt₂
= a(3t₁) + b(3t₂) = a[C(t₁) + b(Ct₂)]
∴ Superposition principle is satisfied.
Hence C(t) = 3t is linear function.

Students can download Maths Chapter 1 Relations and Functions Ex 1.2 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Ex 1.2

Question 1.
Let A = {1, 2, 3, 7} and B = {3, 0, -1, 7}, which of the following are relation from A to B?
(i) R₁ = {(2,1), (7,1)}
(ii) R₂ = {(-1,1)}
(iii) R₃ = {(2,-1), (7, 7), (1,3)}
(iv) R₄ = {(7, -1), (0, 3), (3, 3), (0, 7)}
Answer:
A = {1,2,3,7} B = {3,0,-1, 7}
A × B = {1,2,3} × {3, 0,-1, 7}
A × B = {(1,3) (1,0) (1,-1) (1,7) (2,3) (2, 0)
(2, -1) (2, 7) (3, 3) (3,0) (3,-1)
(3, 7) (7, 3) (7, 0) (7,-1) (7, 7)}

(i) R₁ = {(2, 1)} (7, 1)
It is not a relation, there is no element of (2, 1) and (7, 1) in A × B

(ii) R₂ = {(-1),1)}
It is not a relation, there is no element of
(-1, 1) in A × B

(iii) R₃ = {(2,-1) (7, 7) (1,3)}
Yes, It is a relation

(iv) R₄ = {(7,-1) (0,3) (3, 3) (0,7)}
It is not a relation, there is no element of (0, 3) and (0, 7) in A × B

Question 2.
Let A = {1, 2, 3, 4,…,45} and R be the relation defined as “is square of ” on A. Write R as a subset of A × A. Also, find the domain and range of R.
Solution:
A = {1, 2, 3, 4, . . . 45}, A × A = {(1, 1), (2, 2) ….. (45, 45)}
R – is square of’
R = {(1, 1), (2, 4), (3, 9), (4, 16), (5, 25), (6, 36)}
R ⊂ (A × A)
Domain of R = {1, 2, 3, 4, 5, 6}
Range of R = {1, 4, 9, 16, 25, 36}

Question 3.
A Relation R is given by the set {(x, y)/y = x + 3, x ∈ {0, 1, 2, 3, 4, 5}}. Determine its domain and range.
Answer:
x = {0, 1, 2, 3, 4, 5}
y = x + 3
when x = 0 ⇒ y = 0 + 3 = 3
when x = 1 ⇒ y = 1 + 3 = 4
when x = 2 ⇒ y = 2 + 3 = 5
when x = 3 ⇒ y = 3 + 3 = 6
when x = 4 ⇒ y = 4 + 3 = 7
when x = 5 y = 5 + 3 = 8
R = {(0, 3) (1,4) (2, 5) (3, 6) (4, 7) (5, 8)}
Domain = {0, 1, 2, 3, 4, 5}
Range = {3, 4, 5, 6, 7, 8}

Question 4.
Represent each of the given relations by
(a) an arrow diagram
(b) a graph and
(c) a set in roster form, wherever possible.
(i) {(x,y) | x = 2y,x ∈ {2, 3, 4, 5}, y ∈ {1, 2, 3, 4}
(ii) {(x, y) | y = x + 3, x, y are natural numbers < 10}
Answer:
(i) x = {2, 3, 4, 5} y = {1, 2, 3, 4}
x = 2y
wheny y = 1 ⇒ x = 2 × 1 = 2
when y = 2 ⇒ x = 2 × 2 = 4
when y = 3 ⇒ r = 2 × 3 = 6
when y = 4 ⇒ x = 2 × 4 = 8

(a) Arrow diagram

(b) Graph

(c) Roster form R = {(2, 1) (4, 3)}

(ii) x = {1, 2, 3, 4, 5, 6, 7, 8, 9}
y = {1,2, 3, 4, 5, 6, 7, 8,9}
y = x + 3
when x = 1 ⇒ y = 1 + 3 = 4
when x = 2 ⇒ y = 2 + 3 = 5
when x = 3 ⇒ y = 3 + 3 = 6
when x = 4 ⇒ y = 4 + 3 = 7
when x = 5 ⇒ y = 5 + 3 = 8
when x = 6 ⇒ y = 6 + 3 = 9
when x = 7 ⇒ y = 7 + 3 = 10
when x = 8 ⇒ y = 8 + 3 = 11
when x = 9 ⇒ y = 9 + 3 = 12

R = {(1,4) (2, 5) (3,6) (4, 7) (5, 8) (6, 9)}

(a) Arrow diagram

(b) Graph

(c) Roster form: R = {(1, 4) (2, 5) (3, 6) (4, 7) (5, 8) (6, 9)}

Question 5.
A company has four categories of employees given by Assistants (A), Clerks (C), Managers (M) and an Executive Officer (E). The company provide ₹10,000, ₹25,000, ₹50,000 and ₹1,00,000 as salaries to the people who work in the categories A, C, M and E respectively. If A₁, A₂, A₃, A₄ and A₅ were Assistants; C₁, C₂, C₃, C₄ were Clerks; M₁, M₂, M₃ were managers and E₁, E₂ were Executive officers and if the relation R is defined by xRy, where x is the salary given to person y, express the relation R through an ordered pair and an arrow diagram.
Answer:
Assistants → A₁, A₂, A₃, A₄, A₅
Clerks → C₁, C₂, C₃, C₄
Managers → M₁, M₂, M₃
Executive officers → E₁, E₂

R = {00000, A₁) (10000, A₂) (10000, A₃) (10000, A₄) (10000, A₅)
(25000, C₁) (25000, C₂) (25000, C₃) (25000, C₄)
(50000, M₁) (50000, M₂) (50000, M₃) (100000, E₁) (100000, E₂)}

(a) Arrow diagram

Functions Definition
A relation f between two non – empty sets X and Y is called a function from X to Y if for each x ∈ X there exists only one Y ∈ Y such that (x, y) ∈ f
f = {(x, y) / for all x ∈ X, y ∈ f}
Note: The range of a function is a subset of its co-domain