Bhagya

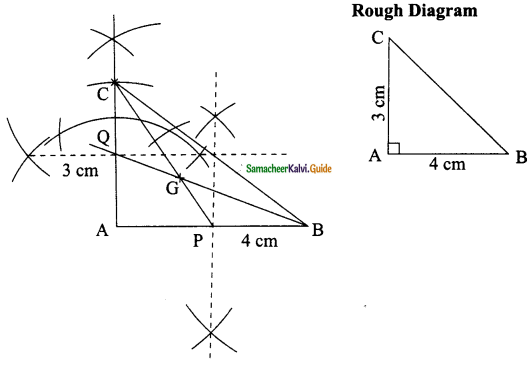
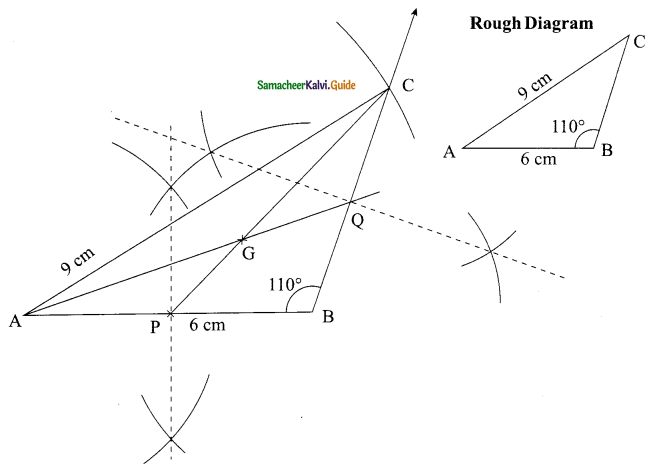
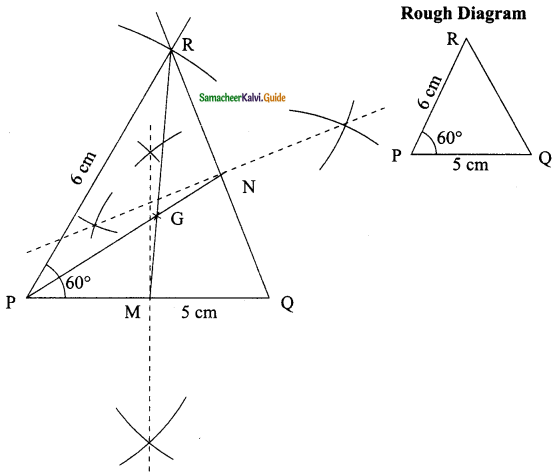
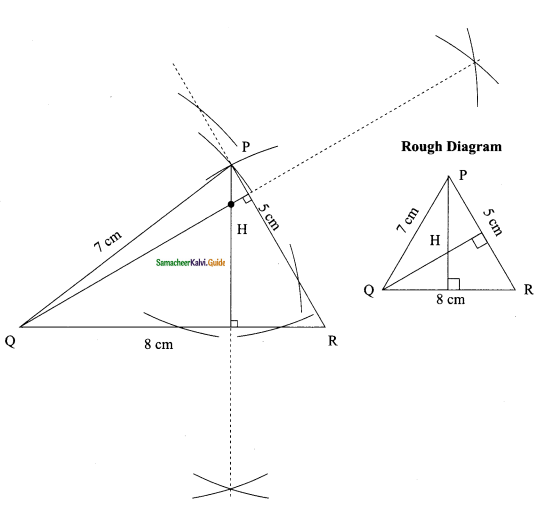
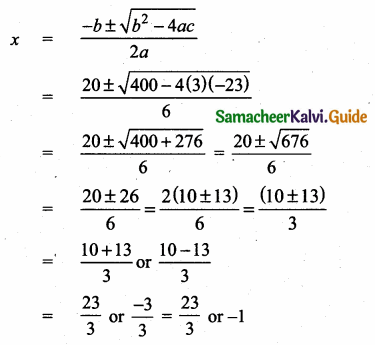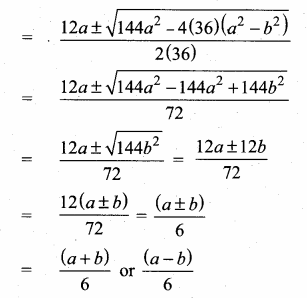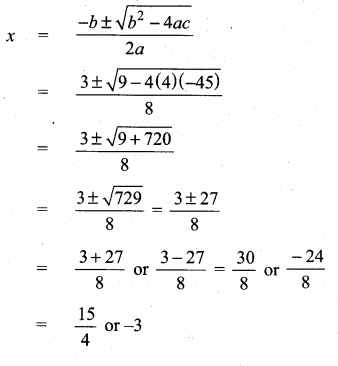Students can download Maths Chapter 4 Geometry Ex 4.7 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.7

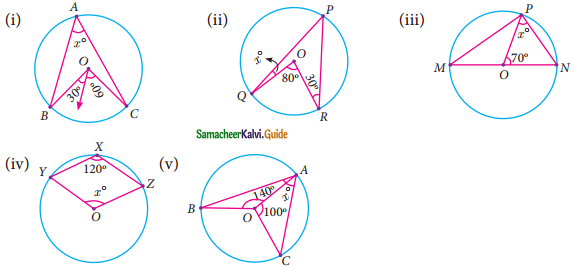
Multiple Choice Questions

Question 1.
The exterior angle of a triangle is equal to the sum of two ……….
(a) Exterior angles
(b) Interior opposite angles
(c) Alternate angles
(d) Interior angles
Solution:
(b) Interior opposite angles

Question 2.
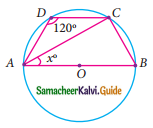
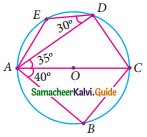
In the quadrilateral ABCD, AB = BC and AD = DC Measure of ∠BCD is …………..

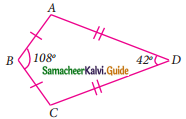
(a) 150°
(b) 30°
(c) 105°
(d) 72°
Solution:
(c) 105°
Hint:
Join BD
∠DBC = 54°; ∠BDC = 21°
∴ ∠BCD = 180° – (54° + 21°)
= 180° – 75°
= 105°

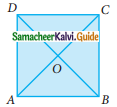
Question 3.
ABCD is a square, diagonals AC and BD meet at O. The number of pairs of congruent triangles with vertex O are ……….

(a) 6
(b) 8
(c) 4
(d) 12
Solution:
(a) 6

Question 4.
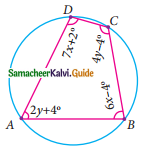
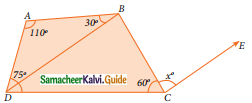
In the given figure CE || DB then the value of x° is ………

(a) 45°
(b) 30°
(c) 75°
(d) 85°
∠B = 360° – (∠A + ∠D + ∠BCD)
= 360° – (110° + 75° + 60°)
= 360° – 245°
= 115°
∠DBC = 115° – 30°
= 85°
∴ ∠x = 85° (BD || CE) Alternate angles are equal

Question 5.
The correct statement out of the following is ……..

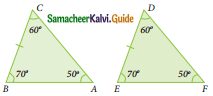
(a) ΔABC ≅ ΔDEF
(b) ΔABC ≅ ΔEDF
(c) ΔABC ≅ ΔFDE
(d) ΔABC ≅ ΔFED
Solution:
(d) ΔABC ≅ ΔFED

Question 6.
If the diagonal of a rhombus are equal, then the rhombus is a ……..
(a) Parallelogram but not a rectangle
(b) Rectangle but not a square
(c) Square
(d) Parallelogram but not a square
Solution:
(c) Square

Question 7.
If bisectors of ∠A and ∠B of a quadrilateral ABCD meet at O, then ∠AOB is ……..
(a) ∠C + ∠D
(b) \(\frac{1}{2}\) (∠C + ∠D)
(c) \(\frac{1}{2}\) ∠C + \(\frac{1}{3}\) ∠D
(d) \(\frac{1}{3}\) ∠C + \(\frac{1}{2}\) ∠D
Solution:
(b) \(\frac{1}{2}\) (∠C + ∠D)

Question 8.
The interior angle made by the side in a parallelogram is 90° then the parallelogram is a …….
(a) rhombus
(b) rectangle
(c) trapezium
(d) kite
Solution:
(b) rectangle
Hint:
Opposite sides are equal and each angle is 90° then it is a rectangle.

Question 9.
Which of the following statement is correct?
(a) Opposite angles of a parallelogram are not equal
(b) Adjacent angles of a parallelogram are complementary.
(c) Diagonals of a parallelogram are always equal.
(d) Both pairs of opposite sides of a parallelogram are always equal.
Solution:
(d) Both pairs of opposite sides of a parallelogram are always equal.

Question 10.
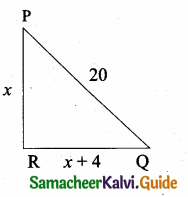
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is ………
(a) 40°
(b) 35°
(c) 50°
(d) 45°
Solution:
(b) 35°
Hint:
3x – 40 + x + 20 + 2x – 10 = 180° (Sum of the angles of a triangle is 180°)
6x – 30 = 180°
6x = 180°+ 30°
x = \(\frac{210°}{6°}\)
= 35°

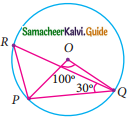
Question 11.
PQ and RS are two equal chords of a circle with centre O such that ∠POQ = 70°, then ∠ORS = ……….
(a) 60°
(b) 70°
(c) 55°
(d) 80°
Solution:
(c) 55°
Hint:

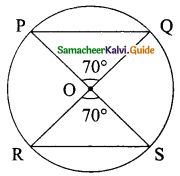
∠POQ = 70° (Vertically opposite Angle)
∠ORS and ∠OSR are equal. (OR = OS radius of the circle)
∠ORS + ∠OSR + ∠ROS = 180°
x° + x° + 70° = 180°
2x + 70° = 180°
2x = 180° – 70° = 110°
x = \(\frac{110°}{2}\) = 55°
∴ ∠ORS = 55°

Question 12.
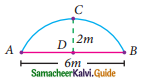
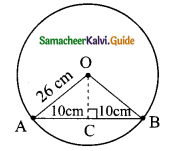
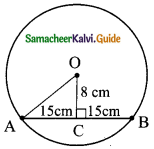
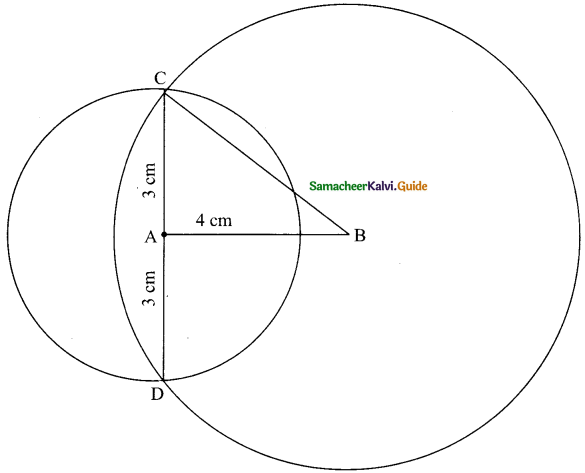
A chord is at a distance of 15cm from the centre of the circle of radius 25cm. The length of the chord is ……….
(a) 25cm
(b) 20cm
(c) 40cm
(d) 18cm
Solution:
(c) 40cm
Hint:

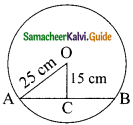
In the right triangle OAC,
AC² = OA² – OC²
= 25² – 15²
= (25 + 15) (25 – 15)
= 40 × 10
AC² = 400
AC = \(\sqrt{400}\)
= 20
Length of the chord AB = 20 + 20 = 40 cm.

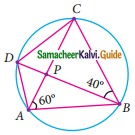
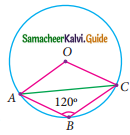
Question 13.
In the figure, O is the centre of the circle and ∠ACB = 40° then ∠AOB = ………

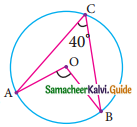
(a) 80°
(b) 85°
(c) 70°
(d) 65°
Solution:
(a) 80°
Hint:
∠AOB = 2∠ACB (The angle subtended by an arc of the circle at the centre is double the angle subtended at the remaining part of the circle.)
= 2 × 40° = 80°

Question 14.
In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is ……..
(a) 30°
(b) 20°
(c) 15°
(d) 25
Solution:
(a) 30°
Hint:

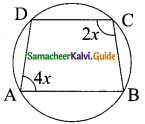
∠A + ∠C = 180° (Sum of the opposite angle of cyclic quadrilateral is 180°)
4x + 2x = 180°
x = \(\frac{180°}{6}\)
= 30°

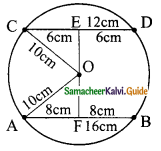
Question 15.
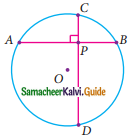
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4cm. The radius of the circle is ………

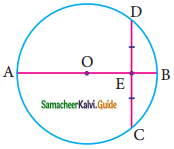
(a) 8cm
(b) 4cm
(c) 6cm
(d) 10cm
Solution:
(i) 10cm
Hint:

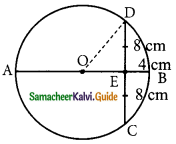
Let the radius OD be x.
OE = OB – BE
= x – 4 (OB radius of the circle)
In the ΔOED,
OD² = OE² + ED²
x² = (x – 4)² + 8²
x² = x² + 16 – 8x + 64
8x = 80
x = \(\frac{80}{8}\)
= 10 cm
Radius of the circle = 10 cm.

Question 16.
In the figure, PQRS and PTVS are two cyclic quadrilaterals, If ∠QRS = 80°, then ∠TVS = ………

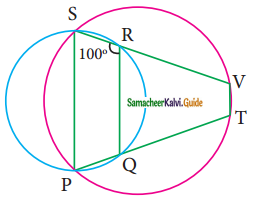
(a) 80°
(b) 100°
(c) 70°
(d) 90°
Solution:
(a) 80°
Hint:
∠SPQ = 180° – 80° (Opposite angles of a cyclic quadrilateral PQRS)
= 100°
In the cyclic quadrilateral PVTS,
∠V = 180° – 100° = 80° (Opposite angles of a cyclic quadrilateral)

Question 17.
If one angle of a cyclic quadrilateral is 75°, then the opposite angle is ………
(a) 100°
(b) 105°
(c) 85°
(d) 90°
Solution:
(b) 105°
Hint:
Opposite angles = 180° – 75°
= 105° (Sum of the opposite angle is 180°)

Question 18.
In the figure, ABCD is a cyclic quadrilateral in which DC produced to E and CF is drawn parallel to AB such that ∠ADC = 80° and ∠ECF = 20°, then BAD = ?

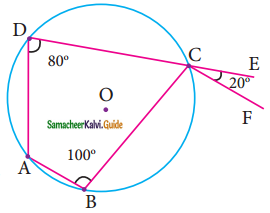
(a) 100°
(b) 20°
(c) 120°
(d) 110°
Solution:
(c) 120°
Hint:
∠BAD = ∠ABC + ∠ECF (By exterior angle property)
= 100° + 20°
= 120°

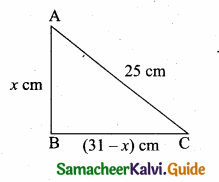
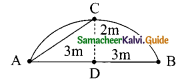
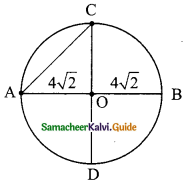
Question 19.
AD is a diameter of a circle and AB is a chord If AD = 30cm and AB = 24cm then the distance of AB from the centre of the circle is ………
(a) 10cm
(b) 9cm
(c) 8cm
(d) 6cm
Solution:
(b) 9cm
Hint:

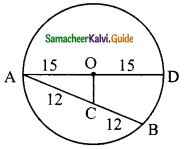
In ΔAOC,
AO = 15 cm
AC = \(\frac{1}{2}\) AB
= \(\frac{1}{2}\) × 24
= 12 cm
In ΔAOC,
OC² = AO² – AC²
= 15² – 12²
= 225 – 144
= 81
OC = \(\sqrt{81}\)
= 9 cm

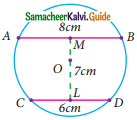
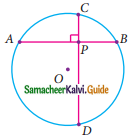
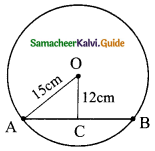
Question 20.
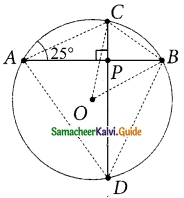
In the given figure, If OP = 17cm, PQ = 30cm and OS is perpendicular to PQ, then RS is ……….

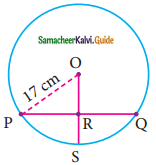
(a) 10cm
(b) 6cm
(c) 7cm
(d) 9cm
Solution:
(d) 9cm
Hint:
In ΔOPR, OP = 17cm, PR = 30/2 = 15 cm.
OR² = OP² – PR²
= 17² – 15²
= (17 + 15) (17 – 15)
= 32 × 2
OR² = \(\sqrt{64}\)
= 8 cm
RS = OS – OR
= 17 – 8
= 9 cm

Students can download Maths Chapter 3 Algebra Ex 3.12 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.12

Question 1.
If the difference between a number and its reciprocal is \(\frac { 24 }{ 5 } \), find the number.
Answer:
Let the number be “x” and its reciprocal is \(\frac { 1 }{ x } \)
By the given condition
x – \(\frac { 1 }{ x } \) = \(\frac { 24 }{ 5 } \)
\(\frac{x^{2}-1}{x}\) = \(\frac { 24 }{ 5 } \)
5x² – 5 = 24x
5x² – 24x – 5 = 0

5x² – 25x + x – 5 = 0 ⇒ 5x (x – 5) + 1(x – 5) = 0
(x – 5) (5x – 1) = 0 ⇒ x – 5 = 0 or 5x + 1 = 0
x = 5 or 5x = -1 ⇒ x = \(\frac { -1 }{ 5 } \)
The number is 5 or \(\frac { -1 }{ 5 } \)

Question 2.
A garden measuring 12m by 16m is to have a pedestrian pathway that is meters wide installed all the way around so that it increases the total area to 285 m². What is the width of the pathway?
Answer:
Let the width of the rectangle be “ω”
Length of the outer rectangle = 16 + (ω + ω)
16 + 2ω
Breadth of the outer rectangle = 12 + 2ω

By the given condition
(16 + 2ω) (12 + 2ω) = 285
192 + 32 ω + 24 ω + 4 ω² = 285
4 ω² + 56ω = 285 – 192
4 ω² + 56 ω = 93
4 ω²+ 56 ω – 93 = 0
Here a = 4, b = 56, c = -93

= 1.5 or -15.5 (Width is not negative)
∴ Width of the path way = 1.5 m

Question 3.
A bus covers a distance of 90 km at a uniform speed. Had the speed been 15 km/hour more it would have taken 30 minutes less for the journey. Find the original speed of the journey.
Answer:
Let the original speed of the bus be “x” km/hr
Time taken to cover 90 km = \(\frac { 90 }{ x } \)
After increasing the speed by 15 km/hr
Time taken to cover 90 km = \(\frac { 90 }{ x+15 } \)
By the given condition
\(\frac { 90 }{ x } \) – \(\frac { 90 }{ x+15 } \) = \(\frac { 1 }{ 2 } \)
\(\frac{90(x+15)-90 x}{x(x+15)}\) = \(\frac { 1 }{ 2 } \)
90x + 1350 – 90x = \(\frac{x^{2}+15 x}{2}\)
1350 = \(\frac{x^{2}+15 x}{2}\)
2700 = x² + 15x

x² + 15x – 2700 = 0
(x + 60) (x – 45) = 0
x + 60 = 0 or x – 45 = 0
x = – 60 or x = 45
The speed will not be negative
∴ Original speed of the bus = 45 km/hr

Question 4.
A girl is twice as old as her sister. Five years hence, the product of their ages – (in years) will be 375. Find their present ages.
Answer:
Let the age of the sister be “x”
The age of the girl = 2x
Five years hence
Age of the sister = x + 5
Age of the girl = 2x + 5
By the given condition
(x + 5) (2x + 5) = 375
2x² + 5x + 10x + 25 = 375
2x² + 15x – 350 = 0
a = 2, b = 15, c = -350

Age will not be negative
Age of the girl = 10 years
Age of the sister = 20 years (2 × 10)

Question 5.
A pole has to be erected at a point on the boundary of a circular ground of diameter 20 m in such a way that the difference of its distances from two diametricallyopposite fixed gates P and Q on the boundary is 4 m. Is it possible to do so? If answer is yes at what distance from the two gates should the pole be erected?
Answer:
Let “R” be the required location of the pole
Let the distance from the gate P is “x” m : PR = “x” m
The distance from the gate Q is (x + 4)m
∴ QR = (x + 4)m
In the right ∆ PQR,

PR² + QR² = PQ² (By Pythagoras theorem)
x² + (x + 4)² = 20²
x² + x² + 16 + 8x = 400
2x² + 8x – 384 = 0

x² + 4x – 192 = 0(divided by 2)
(x + 16) (x – 12) = 0
x + 16 = 0 or x – 12 = 0 [negative value is not considered]
x = -16 or x = 12
Yes it is possible to erect
The distance from the two gates are 12 m and 16 m

Question 6.
From a group of 2x² black bees , square root of half of the group went to a tree. Again eight-ninth of the bees went to the same tree. The remaining two got caught up in a fragrant lotus. How many bees were there in total?
Answer:
Total numbers of black bees = 2x²
Half of the group = \(\frac { 1 }{ 2 } \) × 2x² = x²
Square root of half of the group = \(\sqrt{x^{2}}\) = x
Eight – ninth of the bees = \(\frac { 8 }{ 9 } \) × 2x² = \(\frac{16 x^{2}}{9}\)
Number ofbees in the lotus = 2
By the given condition
x + \(\frac{16 x^{2}}{9}\) + 2 = 2x²
(Multiply by 9) 9x + 16×2 + 18 = 18x²

18x² – 16x² – 9x – 18 = 0 ⇒ 2x² – 9x – 18 = 0
2x² – 12x + 3x – 18 = 0
2x(x – 6) + 3 (x – 6) = 0
(x – 6) (2x + 3) = 0
x – 6 = 0 or 2x + 3 = 0
x = 6 or 2x = -3 ⇒ x = \(\frac { -3 }{ 2 } \) (number of bees will not be negative)
Total number of black bees = 2x² = 2(6)²
= 72

Question 7.
Music is been played in two opposite galleries with certain group of people. In the first gallery a group of 4 singers were singing and in the second gallery 9 singers were singing. The two galleries are separated by the distance of 70 m. Where should a person stand for hearing the same intensity of the singers voice?
(Hint: The ratio of the sound intensity is equal to the square of the ratio of their corresponding distances).
Answer:
Number of singers in the first group = 4
Number of singers in the second group = 9
Distance between the two galleries = 70 m
Let the distance of the person from the first group be x
and the distance of the person from the second group be 70 – x
By the given condition
4 : 9 = x² : (70 – x)² (by the given hint)
\(\frac { 4 }{ 9 } \) = \(\frac{x^{2}}{(70-x)^{2}}\)
\(\frac { 2 }{ 3 } \) = \(\frac { x }{ 70-x } \) [taking square root on both sides]
3x = 140 – 2x
5x = 140
x = \(\frac { 140 }{ 5 } \) = 28
The required distance to hear same intensity of the singers voice from the first galleries is 28m
The required distance to hear same intensity of the singers voice from the second galleries is (70 – 28) = 42 m

Question 8.
There is a square field whose side is 10 m. A square flower bed is prepared in its centre leaving a gravel path all round the flower bed. The total cost of laying the flower bed and gravelling the path at ₹3 and ₹4 per square metre respectively is ₹364. Find the width of the gravel path.
Answer:
Let the width of the gravel path be ‘x’
Side of the flower bed = 10 – (x + x)
= 10 – 2x

Area of the path way = Area of the field – Area of the flower bed
= 10 × 10 – (10 – 2x) (10 – 2x) sq.m
= 100 – (100 + 4x² – 40x)
= 100 – 100 – 4x² + 40x
= 40x – 4x² sq.m
Area of the flower bed = (10 – 2x) (10 – 2x) sq.m.
= 100 + 4x² – 40x
By the given condition

3(100 + 4x² – 40x) + 4(40x – 4x²) = 364
300 + 12x² – 120x + 160x – 16x² = 364
-4x² + 40x + 300 – 364 = 0
-4x² + 40x – 64 = 0
(÷ by 4) ⇒ x² – 10x + 16 = 0
[The width must not be equal to 8 m since the side of the field is 10m]
(x – 8) (x – 2) = 0
x – 8 = 0 or x – 2 = 0 x = 8 or x = 2
Width of the gravel path = 2 m

Question 9.
Two women together took 100 eggs to a market, one had more than the other. Both sold them for the same sum of money. The first then said to the second: “If I had your eggs, I would have earned ₹ 15”, to which the second replied: “If I had your eggs, I would have earned ₹ 6 \(\frac{2}{3}\) How many eggs did each had in the beginning?
Solution:
Let the no. of eggs with woman 1 be x and woman 2 be y.
∴ x + y = 100
Let w₁ sell the eggs at ₹ ‘a’ per egg.
Let w₂ sell the eggs at ₹ ‘b’ per egg.
Case 1:
They sold them for same money.
∴ ax = by
Case 2:
ay = 15 and bx = \(\frac{20}{3}\)
∴ One woman had 40 eggs and the other had 60 eggs.

Question 10.
The hypotenuse of a right angled triangle is 25 cm and its perimeter 56 cm. Find the length of the smallest side.
Answer:
Perimeter of a right angle triangle = 56 cm
Sum of the two sides + hypotenuse = 56
Sum of the two sides = 56 – 25
= 31 cm
Let one side of the triangle be “x”

The other side of the triangle = (31 – x) cm
By Pythagoras theorem
AB² + BC² = AC²
x² + (31 – x)² = 25²
x² + 961 + x² – 62x = 625

2x² – 62x + 961 – 625 = 0
2x² – 62x + 336 = 0 ⇒ x² – 31x + 168 = 0
(x – 24) (x – 7) = 0
x – 24 = 0 (or) x – 7 = 0
x = 24 (or) x = 7
Length of the smallest side is 7 cm

Students can download Maths Chapter 4 Geometry Ex 4.6 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.6

Question 1.
Draw a triangle ABC, where AB = 8 cm, BC = 6 cm and ∠B = 70° and locate its circumcentre and draw the circumcircle.
Solution:

Steps for construction:
Step 1: Draw the ΔABC with the given measures.
Step 2: Construct the perpendicular bisector of (AB and BC) any two sides and let them, meet at S which is the circumcenter.
Step 3: With S as centre and SA = SB = SC as radius draw the circumcircle to passes through A, B and C.
Circum radius = 4.3 cm.

Question 2.
Construct the right triangle PQR whose perpendicular sides are 4.5 cm and 6 cm. Also locate its circumcentre and draw circumcircle.
Solution:

Steps for construction:
Step 1: Draw the ΔPQR with the given measures.
Step 2: Construct the perpendicular bisector of (PQ and PR) any two sides and let them meet at S which is the circumcenter.
Step 3: With S as centre and SP = SQ = SR as radius draw the circumcircle to passes through P, Q and R.
Circum radius = 3.8 cm.

Question 3.
Construct ΔABC with AB = 5 cm ∠B = 100° and BC = 6 cm. Also locate its circumcentre draw circumcircle.
Solution:

Steps for construction:
Step 1: Draw the ΔABC with the given measures.
Step 2: Construct the perpendicular bisector of any two sides (AB and BC) and let them meet at S which is the circumcenter.
Step 3: With S as centre and SA = SB = SC as radius draw the circumcircle to passes through A, B and C.
Circum radius = 4.3 cm.

Question 4.
Construct an isosceles triangle PQR where PQ = PR and ∠Q = 50°, QR = 7cm. Also draw its circumcircle.
Solution:

Given PQ = PR
∴ ∠R = 50° (opposite angles are equal)
Steps for construction:
Step 1: Draw the ΔABC with the given measures.
Step 2: Construct the perpendicular bisector of any two sides (QR and PR) and let them meet at S. S is the circumcenter of ΔPQR.
Step 3: With S as centre SP = SQ = SR as radius. Draw the circumcircle.
Circum radius = 3.5 cm.

Question 5.
Draw an equilateral triangle of side 6.5 cm and locate its incentre. Also draw the incircle.
Solution:

Steps for construction:
Step 1: Draw the ΔABC with the each side measure 6.5 cm.
Step 2: Construct the angles bisectors of any two angles (A and B) and let them meet at I. Then I is the incentre of ΔABC.
Step 3: Draw perpendicular from I to any one of the side (AB) to meet AB at D.
Step 4: With I as centre and ID as radius draw the circle. This circle touches all the sides of the triangle internally.
Step 5: Measure of In-radius = 1.5 cm.

Question 6.
Draw a right triangle whose hypotenuse is 10 cm and one of the legs is 8 cm. Locate its incentre and also draw the incircle
Solution:

Steps for construction:
Step 1: Draw the ΔABC with AB = 8cm, BC = 10 cm and ∠A = 90°.
Step 2: Construct the angle bisectors of any two angles (∠B and ∠C) and let them meet at I. Then I is the incentre of ΔABC.
Step 3: Draw perpendicular from I to any one of the side to meet AB at D.
Step 4: With I as centre and ID as radius draw the circle. This circle touches all the sides of the triangle internally.
Step 5: Measure of In-radius = 1.8 cm.

Question 7.
Draw ΔABC given AB = 9 cm, ∠CAB = 115° and ∠ABC = 40°. Locate its incentre and also draw the incircle. (Note: You can check from the above examples that the incentre of any triangle is always in its interior).
Solution:

Step 1: Draw the ΔABC with AB = 9cm, ∠B = 40° and ∠A = 115°.
Step 2: Construct the angle bisectors of any two angles (A and B) and let them meet at I. Then I is the incentre of ΔABC.
Step 3: Draw perpendicular from I to any one of the side (AB) to meet AB at D.
Step 4: With I as centre and ID as radius draw the circle. This circle touches all the sides of the triangle internally.
Step 5: Measure of In-radius = 2.7 cm.

Question 8.
Construct ΔABC in which AB = BC = 6cm and ∠B = 80°. Locate its incentre and draw the incircle.
Solution:

Steps for construction:
Step 1: Draw the ΔABC with AB = 6 cm, ∠B = 80° and BC = 6 cm.
Step 2: Construct the angle bisectors of any two angles (A and B) and let them meet at I. Then I is the incentre of ΔABC.
Step 3: Draw perpendicular from I to any one of the side (AB) to meet AB at D.
Step 4: With I as centre and ID as radius draw the circle. This circle touches all the sides of the triangle internally.
Step 5: Measure of In-radius = 1.9 cm.

Students can download Maths Chapter 4 Geometry Ex 4.5 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.5

Question 1.
Construct the ΔLMN such that LM = 7.5 cm, MN = 5cm and LN = 8cm. Locate its centroid.
Solution:

Steps for construction:
Step 1: Draw the ΔLMN using the given measurement LM = 7.5 cm, MN = 5cm and LN = 8cm.
Step 2: Construct the perpendicular bisectors of any two sides LM and MN intersect LM at P and MN at Q respectively.
Step 3: Draw the median LQ and PN meet at G.
The point G is the centroid of the given ΔLMN.

Question 2.
Draw and locate the centroid of the triangle ABC where right angle at A, AB = 4cm and AC = 3 cm.
Solution:

Steps for construction:
Step 1: Draw the ΔABC using the given measurement AB = 4cm and AC = 3 cm and ZA = 90°.
Step 2: Construct the perpendicular bisectors of any two sides AB and AC to find the mid-points P and Q of AB and AC.
Step 3: Draw the medians PC and BQ intersect at G.
The point G is the centroid of the given ΔABC.

Question 3.
Draw the ΔABC, where AB = 6cm, ∠B = 110° and AC = 9cm and construct the centroid.
Solution:

Steps for construction:
Step 1: Draw the ΔABC using the given measurement AB = 6cm, AC = 9cm and ∠B =110°.
Step 2: Construct the perpendicular bisectors of any two sides AB and BC to find the mid-points P and Q of AB and BC.
Step 3: Draw the medians PC and AQ intersect at G.
The point G is the centroid of the given ΔABC.

Question 4.
Construct the ΔPQR such that PQ = 5cm, PR = 6cm and ∠QPR = 60° and locate its centroid.
Solution:

Steps for construction:
Step 1 : Draw ΔPQR using the given measurements PQ = 5cm, PR = 6cm and ∠P = 60°.
Step 2 : Construct the perpendicular bisectors of any two sides PQ and QR to find the mid-points of M and N respectively.
Step 3 : Draw the median PN and MR and let them meet at G.
The point G is the centroid of the given ΔPQR.

Question 5.
Draw ΔPQR with sides PQ = 7 cm, QR = 8 cm and PR = 5 cm and construct its Orthocentre.
Solution:

Steps for construction:
Step 1: Draw the ΔPQR with the given measurements.
Step 2: Construct altitudes from any two vertices P and Q to their opposite sides QR and PR respectively.
Step 3: The point of intersection of the altitude H is the orthocentre of the given ΔPQR.

Question 6.
Draw an equilateral triangle of sides 6.5 cm and locate its Orthocentre.
Solution:

Steps for construction:
Step 1: Draw the ΔABC with the given measurements.
Step 2: Construct altitudes from any two vertices A and C to their opposite sides BC and AB respectively.
Step 3: The point of intersection of the altitude H is the orthocentre of the given ΔABC.

Question 7.
Draw ΔABC, where AB = 6 cm, ∠B = 110° and BC = 5 cm and construct its Orthocentre.
Solution:

Steps for construction:
Step 1: Draw the ΔABC with the given measurements.
Step 2: Construct altitudes from any two vertices B and C to their opposite sides AC and BC respectively.
Step 3: The point of intersection of the altitude H is the orthocentre of the given ΔABC.

Question 8.
Draw and locate the Orthocentre of a right triangle PQR where PQ = 4.5 cm, QR = 6 cm and PR = 7.5 cm.
Solution:

Steps for construction:
Step 1: Draw the ΔPQR with the given measures.
Step 2: Construct altitude from any two vertices Q and R to their opposite side PR and PQ respectively.
Step 3: The point of intersection of the altitude H is the orthocentre of the given ΔPQR.

Students can download Maths Chapter 4 Geometry Ex 4.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.4

Question 1.
Find the value of x in the given figure.

Solution:
∠B = 180° – 120°
(Sum of the opposite angles of a quadrilateral are supplementary)
∠B = 60°
∠BCA = 90° (Angle in a semicircle)
∠BAC + ∠B + ∠BCA = 180°
x + 60° + 90° = 180°
x + 150° = 180°
x = 180° – 150°
= 30°
The value of x = 30°

Question 2.
In the given figure, AC is the diameter of the circle with centre O.

If ∠ADE = 30°; ∠DAC = 35° and ∠CAB = 40°.
Find (i) ∠ACD
(ii) ∠ACB
(iii) ∠DAE
Solution:
(i) ∠ADC = 90° (Angle in a semi-circle)
∠ADC + ∠ACD + ∠DAC = 180° (Sum of the angles of a triangle is 180°)
90° + ∠ACD + 35° = 180°
∠ACD = 180° – 125°
∠ACD = 55°

(ii) ∠ABC = 90° (Angle in a semi-circle)
∠ACB + ∠CBA + ∠BAC = 180° (Sum of the angles of a triangle is 180°)
∠ACB + 90 °+ 40° = 180°
∠ACB = 180° – 130°
= 50°

(iii) In the cyclic quadrilateral ACDE,
∠AED = 180° – 55°
= 125°
In ΔAED,
∠DAE + ∠AED + ∠EDA = 180° (Sum of the angles of a triangle is 180°)
∠DAE + 125° + 30° = 180°
∠DAE = 180°- 155°
= 25°
∴ ∠DAE = 25°

Question 3.
Find all the angles of the given cyclic quadrilateral ABCD in the figure.

Solution:
In a cyclic quadrilateral ABCD,
∠B + ∠D = 180° (Sum of the opposite angles of a cyclic quadrilateral is 180°)
6x – 4° + 7x + 2° = 180°
13x – 2° = 180°
13x = 182°
x = 182°
x = \(\frac{182°}{13}\)
x = 14°
∠B = 6x – 4°
= 6(14) – 4°
= 84 – 4
= 80°
∠D = 7x + 2°
7(14) + 2°
98 + 2
= 100°
180°
2y + 4° + 4y – 4° = (Sum of the opposite angles of a cyclic quadrilateral is 180°)
6y = 180°
y = \(\frac{180°}{6}\)
= 30°
∠A = 2y + 4°
= 2(30) + 4°
= 64°
∠C = 4y – 4°
= 4(30) – 4°
= 120° – 4°
= 116°
∴ ∠A = 64°, ∠B = 80°, ∠C = 116°, ∠D = 100°.

Question 4.
In the given figure, ABCD is a cyclic quadrilateral where diagonals intersect at P such that ∠DBC = 40° and ∠BAC = 60° find

(i) ∠CAD
(ii) ∠BCD
Solution:
(i) ∠CAD = ∠DBC = 40° [Angles at the circumference to the same segment]
(ii) ∠BAC – ∠BDC = 60° [Angles at the circumference to the same segment]
∠BCD + ∠BDC + ∠CBD = 180° (Sum of the three angles of A is 180°)
∠BCD + 60° + 40° = 180°
∠BCD = 180° – 100°
= 80°

Question 5.
In the given figure, AB and CD are the parallel chords of a circle with centre O. Such that AB = 8 cm and CD = 6 cm. If OM ⊥ AB and OL ⊥ CD distance between LM is 7cm. Find the radius of the circle?

Solution:
Let OM be x.
∴ OL = 7 – x
In the right ΔAOM,
OA² = AM² + OM²
= 4² + x²
OA² = 16 + x²
r² = 16 + x² ……… (1) [r is the radius]
In the right ΔOCL,
OC² = OL² + CL²
r² = (7 – x)² + 3²
= 49 + x² – 14x + 9
= 58 + x² – 14x …….. (2)
From (1) and (2) we get,
16 + x² = 58 + x² – 14x
14x = 58 – 16
14x = 42
x = \(\frac{42}{14}\)
x = 3 cm
r² = 16 + x²
= 16 + 9
= 25
∴ r = \(\sqrt{25}\)
= 5
∴ radius of the circle = 5 cm.

Question 6.
The arch of a bridge has dimensions as shown, where the arch measure 2 m at its highest point and its width is 6 cm. What is the radius of the circle that contains the arch?

Solution:
AD = \(\frac{6}{2}\)
= 3 m
In the right ΔADC,

AC² = AD² + DC²
= 32 + 22
= 9 + 4
= 13
AC = \(\sqrt{13}\)
= 3.6m
radius = 3.6 m

Question 7.
In figure ∠ABC = 120°, where A, B and C are points on the circle with centre O. Find ∠OAC?

Solution:
Reflex ∠AOC = 2∠ABC
= 20 × 120°
= 240°
∴ ∠AOC = 360° – 240°
= 120°
∠OCA + ∠OAC = 180° – 120°
= 60°
∴ ∠OAC = \(\frac{60}{2}\)
= 30° (Since OA = OC)

Question 8.
A school wants to conduct tree plantation programme. For this a teacher allotted a circle of radius 6m ground to nineth standard students for planting sapplings. Four students plant trees at the points A, B, C and D as shown in figure. Here AB = 8m, CD = 10m and AB ⊥ CD. If another student places a flower pot at the point P, the intersection of AB and CD, then find the distance from the centre to P.

Solution:
OA = OD = 6 m
AB = 8 m (chord)
CD = 10 m (chord)
In Δ AOM, OM = \(\sqrt{6² – 4²}\) (∴ OM bisects the chord and ⊥ to the chord)
= \(\sqrt{36 – 16}\)
= \(\sqrt{20}\)m
In Δ CON, ON = \(\sqrt{6² – 5²}\)
= \(\sqrt{36 – 25}\)
= \(\sqrt{11}\)m (ON bisects the chord and ⊥ to the chord)
ONPM is a rectangle with all the angles 90° and with length \(\sqrt{20}\) m, breadth \(\sqrt{11}\)l m.
We need to find OP which is the diagonal of the rectangle ONPM.
∴ OP = \(\sqrt{ON² + NP²}\) = \(\sqrt{(\sqrt{11})² + (\sqrt{20})²}\)
(∴ OM = NP, opposite sides of the rectangle)
= \(\sqrt{11 + 20}\)
= \(\sqrt{31}\)
= 5.56 m

Question 9.
In the given figure, ∠POQ = 100° and ∠PQR° = 30°, then find ∠RPO.

Solution:
∠PRQ = \(\frac{1}{2}\) ∠POQ (Angles at the circumference)
= \(\frac{1}{2}\) × 100°
= 50°
∠OPQ + ∠OQP = 180° – 100° (Total angles of A is 180°)
= 80°
∴ ∠OPQ = \(\frac{80}{2}\)
= 40° (Since OP = OQ, radius of the circle)
∠RPQ = 180°- (30 + 50)°
= 100°
∴ ∠RPO = ∠RPQ – ∠OPQ
= 100° – 40°
= 60°

Students can download Maths Chapter 3 Algebra Ex 3.11 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.11

Question 1.
Solve the following quadratic equations by completing the square method
(i) 9x² – 12x + 4 = 0
Answer:
9x² – 12x + 4 = 0
x² – \(\frac { 12x }{ 9 } \) + \(\frac { 4 }{ 9 } \) = 0 (Divided by 9)
x² – \(\frac { 4x }{ 3 } \) = \(\frac { -4 }{ 9 } \)
Add [\(\frac { 1 }{ 2 } \) (\(\frac { 4 }{ 3 } \))]² on both sides

The solution is \(\frac { 2 }{ 3 } \)

(ii) \(\frac { 5x+7 }{ x-1 } \) = 3x + 2
Answer:
(3x + 2) (x – 1) = 5x + 7
3x² – 3x + 2x – 2 = 5x + 7 ⇒ 3x² – x – 5x – 2 – 7 = 0
3x² – 6x – 9 = 0 ⇒ x² – 2x – 3 = 0 (divided by 3)
x² – 2x = 3
Adding (\(\frac { 1 }{ 2 } \) × 2)² on both sides
x² – 2x + 1 = 3 + 1
(x – 1)² = 4 ⇒ x – 1 = \(\sqrt { 4 }\)
x – 1 = ±2
x – 1 = 2 or x – 1 = -2
x = 3 or x = -1
The solution set is -1 and 3

Question 2.
Solve the following quadratic equations by formula method
(i) 2x² – 5x + 2 = 0
Answer:
a = 2, b = -5, c = 2

The solution set is \(\frac { 1 }{ 2 } \) and 2

(ii) \(\sqrt { 2 }\) f² – 6 f + 3 \(\sqrt { 2 }\) = 0
Answer:
Here a = \(\sqrt { 2 }\), b = -6 and c = 3\(\sqrt { 2 }\)

The solution set is \(\frac{3+\sqrt{3}}{\sqrt{2}}\) and \(\frac{3-\sqrt{3}}{\sqrt{2}}\)

(iii) 3y² – 20y – 23 = 0
Answer:
a = 3, b = -20, c = -23

The solution set is -1 and \(\frac { 23 }{ 3 } \)

(iv) 36y² – 12ay + (a² – b²) = 0
Answer:
Here a = 36, b = -12a, c = a² – b²

The solution set is \(\frac { (a+b) }{ 6 } \) and \(\frac { (a-b) }{ 6 } \)

Question 3.
A ball rolls down a slope and travels a distance d = t² – 0.75t feet in t seconds. Find the time when the distance travelled by the ball is 11.25 feet.
Answer:
Distance = t² – 0.75t
11.25 = t² – 0.75t
Multiply by 100
1125 = 100t² – 75t
100t² – 75t – 1125 = 0 (Divided by 25)
4t² – 3t – 45 = 0
a = 4,
b = -3,
c = -45

(time will not be negative)
The required time = \(\frac { 15 }{ 4 } \) seconds
= 3 \(\frac { 3 }{ 4 } \) second or 3.75 seconds

Students can download Maths Chapter 4 Geometry Ex 4.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.3

Question 1.
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre.
Radius of a circle = \(\frac{56}{2}\) = 26 cm
Solution:

Length of the chord = 20 cm
AC = \(\frac{20}{2}\)
= 10 cm
In ΔOAC, OC² = OA² – AC²
= 26² – 10²
= (26 + 10) (26 – 10)
= 36 × 16
OC = \(\sqrt{30×16}\)
= 6 × 4 cm
= 24 cm
Distance of the chord from the centre = 24 cm.

Question 2.
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle.
Solution:

Distance AC = \(\frac{1}{2}\) × Length of chord
= \(\frac{1}{2}\) × 30
= 15 cm
Distance from the centre = 8 cm
In ΔOAC Radius (OA) = \(\sqrt{AC² + OC²}\)
= \(\sqrt{15² + 8²}\)
= \(\sqrt{224 + 64}\)
= \(\sqrt{289}\)
= 17
Radius of the circle = 17 cm.

Question 3.
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius 4√2 cm and also find ∠OAC and ∠OCA.
Solution:
Radius of a circle = 4√2 cm
In the right ΔAOC,

AC² = OA² + OC²
AC² = (4√2)² + (4√2)²
= 32 + 32 = 64
AC = \(\sqrt{64}\)
= 8
Length of the chord = 8 cm,
∠OAC = ∠OCA = 45°
Since OAC is an isosceles right angle triangle.

Question 4.
A chord is 12 cm away from the centre of the circle of radius 15cm. Find the length of the chord.
Solution:
Radius of a circle (OA) = 15 cm
Distance from centre to the chord (OC) = 12 cm
In the right ΔOAC,

AC² = OA² – OC²
= 15² – 12²
= 225 – 144
= 81
AC = \(\sqrt{81}\)
= 9
Length of the chord (AB) = AC + CB
= 9 + 9 = 18 cm.

Question 5.
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
Solution:
Length of the chord (AB) = 16 cm
∴ AF = \(\frac{1}{2}\) × 16
= 8 cm
Length of the chord (CD) = 12 cm
∴ CE = \(\frac{1}{2}\) × 12
= 6 cm

In the right ΔOCE,
OE² = OC² – CE²
= 10² – 6²
= 100 – 36
= 64
OE = \(\sqrt{64}\)
= 8 cm
In the right ΔOAF,
OF² = OA² – AF²
= 10² – 8²
= 100 – 64
= 36
OE = \(\sqrt{36}\)
= 6 cm
Distance between the two chords = OE + OF
= 8 + 6
= 14 cm.

Question 6.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Ans

Two circules intersect at C and D
CD is the common chord.
CD = AC + AD
= 3 + 3
= 6 cm
Length of the common chord = 6 cm.

Question 7.
Find the value of x° in the following figures:

Solution:
(i) ∠BOC = 30° + 60°
= 90°
∠BAC (x) = \(\frac{1}{2}\) ∠BOC (By theorem)
= \(\frac{1}{2}\) × 90°
x = 45°

(ii) Join OP
∠QPR = \(\frac{80}{2}\) = 40° (Angle of the circumference is \(\frac{1}{2}\) the angle at the centre)
∠RPO = 30° (OP and OR are equal sides)
∠OPQ = 40° – 30°
= 10°
∠OQP = 10° (OQ and OP are equal sides)
∴ x = 10°

(iii) ∠OPN = ∠ONP (ON and OP are the radius of the circle)
= 90°
In ΔOPN
∠PON + ∠ONP + ∠NPO = 180° (Sum of the angles of a triangle)
70° + x° + x° = 180°
2x° + 70° = 180°
2x = 180° – 70°
2x = 110°
X = \(\frac{110°}{2}\)
= 55°
The value of x = 55°

(iv) Reflex ∠YOZ = 2∠YXZ
= 2(120°)
= 240°
∠YOZ = 360° – reflex ∠YOZ
= 360° – 240°
= 120°
∴ x = 120°

(v) ∠OAC + ∠OCA = 180° – 100°
= 80°
∠OAC = \(\frac{1}{2}\) × 80° [Since OA = OC, (∴ ∠OAC = ∠OCA)]
= 40°
∠OBA + ∠OAB = 180° – 140°
= 40° [Since ∠OBA = ∠OAB, since OB = OA]
∴∠OAB = \(\frac{40°}{2}\)
= 20°
∠BAC = ∠OAB + ∠OAC
= 20° + 40°
x = 60°

Question 8.
In the given figure, ∠CAB = 25°, find ∠BDC, ∠DBA and ∠COB.

Solution:
In ΔACP,
∠ACP = 180° – (25° + 90°)
= 180° – 115°
= 65°
∠CBA = ∠CAB = 25° [Both the angles are standing in the same base]
∠DBA = 65° [∠DBA and ∠BCA standing in the same base]
∠COB = 50°

Students can download Maths Chapter 3 Algebra Ex 3.10 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.10

Question 1.
Solve the following quadratic equations by factorization method
(i) 4x² – 7x – 2 = 0
Answer:
4x² – 7x – 2 = 0
4x² – 8x + x – 2 = 0
4x(x – 2) + 1(x – 2) = 0
(x – 2) + (4x + 1) = 0

x – 2 = 0 or 4x + 1 = 0 (equate the product of factors to zero)
x = 2 or 4x = -1 ⇒ x = \(\frac { -1 }{ 4 } \)
The roots are 2; \(\frac { -1 }{ 4 } \)

(ii) 3(p² – 6) = p(p + 5)
Answer:
3p² – 18 = p² + 5p

2p² – 5p – 18 = 0
2p² – 9p + 4p – 18 = 0
p(2p – 9) + 2(2p – 9) = 0
(2p – 9)(p + 2) = 0
2p – 9 = 0 or p + 2 =
The roots are p = \(\frac { 9 }{ 2 } \), -2

(iii) \(\sqrt{a(a-7)}\) = 3 \(\sqrt{2}\)
Answer:
Squaring on both sides
a(a – 7) = (3\(\sqrt{2}\))²

a² – 7a = 18
a² – 7a – 18 = 0
(a – 9) (a + 2) = 0
a – 9 = 0 or a + 2 = 0
The roots are -2 and 9

(iv) \(\sqrt { 2 }\) x² + 7x + 5\(\sqrt { 2 }\) = 0
Answer:
\(\sqrt { 2 }\) x² + 7x + 5 \(\sqrt { 2 }\) = 0
\(\sqrt { 2 }\) x² + 2x + 5x + 5\(\sqrt { 2 }\) = 0
\(\sqrt { 2 }\) x (x + \(\sqrt { 2 }\)) + 5(x + \(\sqrt { 2 }\)) = 0

(x + \(\sqrt { 2 }\)) + (\(\sqrt { 2 }\)x + 5) = 0 (equate the product of factors to zero)
x + – \(\sqrt { 2 }\) = 0 or \(\sqrt { 2 }\)x + -5
x = \(\frac{-5}{\sqrt{2}}\)
The roots are – \(\sqrt { 2 }\), \(\frac{-5}{\sqrt{2}}\)

(v) 2x² – x + \(\frac { 1 }{ 8 } \) = 0
Answer:
2x² -x + \(\frac { 1 }{ 8 } \) = 0
16x² – 8x + 1 = (multiply by 8)

16x² – 4x – 4x + 1
4x(4x – 1) – 1 (4x – 1) = 0
(4x- 1) (4x- 1) = 0
4x = 1, 4x = 1
x = \(\frac { 1 }{ 4 } \), x = \(\frac { 1 }{ 4 } \)
The roots are \(\frac { 1 }{ 4 } \) and \(\frac { 1 }{ 4 } \)

Question 2.
The number of volleyball games that must be scheduled in a league with n teams is given by G(n) = \(\frac{n^{2}-n}{2}\) where each team plays with every other team exactly once. A league schedules 15 games. How many teams are in the league?
Solution:
G(n) = \(\frac{n^{2}-n}{2}\)
⇒ 15 = \(\frac{n^{2}-n}{2}\) ⇒ 30 = n² – n
n² – n – 30 = 0
⇒ n² – 6n + 5n – 30 = 0
n(n – 6) + 5 (n – 6) = 0
(n – 6)(n + 5) = 0 ⇒ n = 6, -5
As n cannot be (-ve), n = 6.
∴ There are 6 teams in the league.

Students can download Maths Chapter 3 Algebra Ex 3.4 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.4

Question 1.
Reduce each of the following rational expression to its lowest form.
(i) \(\frac{x^{2}-1}{x^{2}+x}\)
Answer:
\(\frac{x^{2}-1}{x^{2}+x}\) = \(\frac{(x+1)(x-1)}{x(x+1)}\) = \(\frac { x-1 }{ x } \)

(ii) \(\frac{x^{2}-11 x+18}{x^{2}-4 x+4}\)

x² – 11x + 18 = (x – 9) (x – 2)
x² – 4x + 4 = (x – 2) (x – 2)

(iii) \(\frac{9 x^{2}+81 x}{x^{3}+8 x^{2}-9 x}\)
9x² + 81x = 9x(x + 9)
x³ + 8x² – 9x = x(x² + 8x – 9)
= x (x + 9) (x – 1)

(iv) \(\frac{p^{2}-3 p-40}{2 p^{3}-24 p^{2}+64 p}\)
p² – 3p – 40 = (p – 8) (p + 5)
2p³ – 24p² + 64p = 2p (p² – 12p + 32)
= 2p (p – 8) (p – 4)

Question 2.
Find the excluded values , if any of the following expressions.

(i) \(\frac{y}{y^{2}-25}\)
Answer:
The expression \(\frac{y}{y^{2}-25}\) is undefined
when y² – 25 = 0
y² – 5² = 0
(y + 5) (y – 5) = 0
y + 5 = 0 or y – 5 = 0
∵ y = -5 or y = 5
The excluded values are -5 and 5

(ii) \(\frac{t}{t^{2}-5 t+6}\)
Answer:
The expression \(\frac{t}{t^{2}-5 t+6}\) is undefined
when t² – 5t + 6 = 0
(t – 3) (t – 2) = 0

t – 3 = 0 or t – 2 = 0
t = 3 or t = 2
The excluded values are 2 and 3

(iii) \(\frac{x^{2}+6 x+8}{x^{2}+x-2}\)
Answer:
x² + 6x + 8 = (x + 4) (x + 2)
x² + x – 2 = (x + 2) (x – 1)


The expression \(\frac { x+4 }{ x-1 } \) is undefined
when x – 1 = 0
∵ x = 1
The excluded value is 1

(iv) \(\frac{x^{3}-27}{x^{3}+x^{2}-6 x}\)
x³ – 27 = x³ – 3³
= (x – 3) (x² + x + 3)
x³ + x² – 6x = x(x² + x – 6) = x (x + 3) (x – 2)


when x (x + 3) (x – 2) = 0
x = 0 or x + 3 = 0 or x – 2 = 0
x = 0 or x = -3 or x = 2
The excluded values are 0 , -3 and 2

Students can download Maths Chapter 3 Algebra Ex 3.12 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.12

Question 1.
Solve by the method of elimination
(i) 2x – y = 3; 3x + y = 7
Solution:
2x – y = 3 → (1)
3x + y = 7 → (2)
By adding (1) and (2)
5x + 0 = 10
x = \(\frac{10}{5}\)
x = 2
Substitute the value of x = 2 in (1)
2(2) – y = 3
4 – y = 3
-y = 3 – 4
-y = -1
y = 1
The value of x = 2 and y = 1

(ii) x – y = 5; 3x + 2y = 25
Solution:
x – y = 5 → (1)
3x + 2y = 25 → (2)
(1) × 2 ⇒ 2x – 2y = 10 → (3)
(2) × 1 ⇒ 3x + 2y = 25 → (2)
(3) + (2) ⇒ 5x + 0 = 35
x = \(\frac{35}{5}\)
= 7
Substitute the value of x = 7 in (1)
x – y = 5
7 – y = 5
-y = 5 – 7
-y = -2
y = 2
∴ The value of x = 7 and y = 2

(iii) \(\frac{x}{10}\) + \(\frac{y}{5}\) = 14; \(\frac{x}{8}\) + \(\frac{y}{6}\) = 15
Solution:
\(\frac{x}{10}\) + \(\frac{y}{5}\) = 14
LCM of 10 and 5 is 10
Multiply by 10
x + 2y = 140 → (1)
\(\frac{x}{8}\) + \(\frac{y}{6}\) = 15
LCM of 8 and 6 is 24
3x + 4y = 360 → (2)
(1) × 2 ⇒ 2x + 4y = 280 → (3)
(2) × 1 ⇒ 3x + 4y = 360 → (2)
(3) – (2) ⇒ -x + 0 = -80
∴ x = 80
Substitute the value of x = 80 in (1)
x + 2y = 140
80 + 2y = 140
2y = 140 – 80
2y = 60
y = \(\frac{60}{2}\)
y = 30
∴ The value of x = 80 and y = 30

(iv) 3(2x + y) = 7xy; 3(x + 3y) = 11xy
Solution:
3(2x + y) = 7xy
6x + 3y = 7xy
Divided by xy

3a + 6b = 7 → (1)
3(x + 3y) = 11xy
3x + 9y = 11xy
Divided by xy

9a + 3b = 11 → (2)
(1) × 3 ⇒ 9a + 18b = 21 → (3)
(2) × 1 ⇒ 9a + 3b = -11 → (2)
(3) – (2) ⇒ 15b = 10
b = \(\frac{10}{15}\) = \(\frac{2}{3}\)
Substitute the value of b = \(\frac{2}{3}\) in (1)
3a + 6 × \(\frac{2}{3}\) = 7
3a + 4 = 7
3a = 7 – 4
3a = 3
a = \(\frac{3}{3}\)
= 1
But \(\frac{1}{x}\) = a
\(\frac{1}{x}\) = 1
x = 1
But \(\frac{1}{y}\) = b
\(\frac{1}{y}\) = \(\frac{2}{3}\)
2y = 3
y = \(\frac{3}{2}\)
∴ The value of x = 1 and y = \(\frac{3}{2}\)

(v) \(\frac{4}{x}\) + 5y = 7; \(\frac{3}{x}\) + 4y = 5
Solution:
Let \(\frac{1}{x}\) = a
4a + 5y = 7 → (1)
3a + 4y = 5 → (2)
(1) × 4 ⇒ 16a + 20y = 28 →(3)
(2) × 5 ⇒ 15a + 20y = 25 → (4)
(3) – (4) ⇒ a + 0 = 3
a = 3
Substitute the value of a = 3 in (1)
4(3) + 5y = 7
5y = 7 – 12
5y = -5
5y = \(\frac{-5}{5}\) = -1
But \(\frac{1}{x}\) = a
\(\frac{1}{x}\) = 3
3x = 1 ⇒ x = \(\frac{1}{3}\)
The value of x = \(\frac{1}{3}\) and y = -1

(vi) 13x + 11y = 70; 11x + 13y = 74
Solution:
13x + 11y = 70 → (1)
11x + 13y = 74 → (2)
(1) + (2) ⇒ 24x + 24y = 144
x + y = 6 → (3) (Divided by 24)
(1) – (2) ⇒ 2x – 2y = -4
x – y = -2 → (4) (Divided by 2)
(4) + (3) ⇒ 2x = 4
x = \(\frac{4}{2}\)
= 2
Substitute the value x = 2 in (3)
2 + y = 6
y = 6 – 2
= 4
∴ The value of x = 2 and y = 4

Question 2.
The monthly income of A and B are in the ratio 3 : 4 and their monthly expenditures are in the ratio 5 : 7. If each saves Rs 5,000 per month, find the monthly income of each.
Solution:
Let the income of “A” be “x” and the income of “B” be “y”.
By the given first condition
x : y = 3 : 4
4x = 3y (Product of the extreme is equal to the product of the means)
4x – 3y = 0 → (1)
Expenditure of A = x – 5000
Expenditure of B = y – 5000
By the given second condition
x – 5000 : y – 5000 = 5 : 7
7(x – 5000) = 5(y – 5000)
7x – 35000 = 5y – 25000
7x – 5y = -25000 + 35000
7x – 5y = 10000 → (2)
(1) × 5 ⇒ 20x – 15y = 0 → (3)
(2) × 3 ⇒ 21x – 15y = 30000 → (4)
(3) – (4) ⇒ x + 0 = 30000
x = 30000
Substitute the value of x in (1)
4 (30000) – 3y = 0
120000 = 3y
y = \(\frac{120000}{3}\) = 40000
∴ Monthly income of A is Rs 30,000
Monthly income of B is Rs 40,000

Question 3.
Five years ago, a man was seven times as old as his son, while five year hence, the man will be four times as old as his son. Find their present age.
Solution:
Let the age of a man be “x” and the age of a son be “y”
5 years ago
Age of a man = x – 5 years
Age of his son = y – 5 years
By the given first condition
x – 5 = 7(y – 5)
x – 5 = 7y – 35
x – 7y = -35 + 5
x – 7y = -30 → (1)
Five years hence
Age of a man = x + 5 years
Age of his son = y + 5 years
By the given second condition
x + 5 = 4 (y + 5)
x + 5 = 4y + 20
x – 4y = 20 – 5
x – 4y = 15 → (2)
(1) – (2) ⇒ -3y = -45
3y = 45
y = \(\frac{45}{3}\)
= 15
Substitute the value of y = 15 in (1)
x – 7(15) = -30
x – 105 = -30
x = -30 + 105
= 75
Age of the man is 75 years
Age of his son is 15 years