Bhagya

Students can download Maths Chapter 3 Ratio and Proportion Ex 3.1 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 3 Ratio and Proportion Ex 3.1

Question 1.
Fill in the blanks.
(i) Ratio of ₹ 3 to ₹ 5 = ____
(ii) Ratio of 3 m to 200 cm = ______
(iii) Ratio of 5 km 400 m to 6 km = ____
(iv) Ratio of 75 paise to ₹ 2 = ____
Solution:
(i) 3 : 5
(ii) 3 : 2
Hint: 3m = 300 cm
(iii) 9 : 10
Hint: 5km 400 m = 5400m and 6 km = 6000 m
(iv) 3 : 8
Hint: ₹ 2 = 200 paise

Question 2.
Say whether the following statements are True or False.
(i) The ratio of 130 cm to 1 m is 13 : 10
(ii) One of the terms in a ratio cannot be 1
Solution:
(i) True
Hint: 1m = 100 cm
(ii) False

Question 3.
Find the simplified form of the following ratios.
(i) 15 : 20
(ii) 32 : 24
(iii) 7 : 15
(iv) 12 : 27
(v) 75 : 100
Solution:
(i) 15 : 20
= \(\frac{15}{20}\)
= \(\frac{3}{4}\)
= 3 : 4

(ii) 32 : 24
= \(\frac{32}{24}\)
= \(\frac{4}{3}\)
= 4 : 3

(iii) 7 : 15

(iv) 12 : 27
= \(\frac{12}{27}\)
= \(\frac{4}{9}\)
= 4 : 9

(v) 75 : 100
= \(\frac{75}{100}\)
= \(\frac{3}{4}\)
= 3 : 4

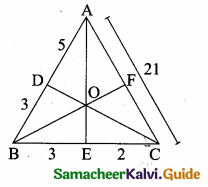
Question 4.
Akilan walks 10 km in an hour while Selvi walks 6 km in an hour. Find the simplest ratio of the distance covered by Akilan to that of Selvi.
Solution:
Ratio of the distance covered by Akilan to that of Selvi = 10 km : 6 km
= \(\frac{10}{6}\)
= \(\frac{5}{3}\)
= 5 : 3

Question 5.
The cost of parking a bicycle is Rs 5 and the cost of parking a scooter is Rs 15. Find the simplest ratio of the parking cost of a bicycle to that of a scooter.
Solution:
Ratio of the parking cost of a bicycle to that of a scooter = Rs 5 : Rs 15
= \(\frac{5}{15}\)
= \(\frac{1}{3}\)
= 1 : 3

Question 6.
Out of 50 students in a class, 30 are boys. Find the ratio of
(i) number of boys to the number of girls.
(ii) the number of girls to the total number of students.
(iii) the number of boys to the total number of students.
Solution:
Total no of students = 50
No of boys = 30
No of girls = 50 – 30 = 20
(i) Ratio of boys to girls = 30 : 20
= \(\frac{30}{20}\)
= \(\frac{3}{2}\)
= 3 : 2

(ii) Ratio of girls to the total number of students = 20 : 50
= \(\frac{20}{50}\)
= \(\frac{2}{5}\)
= 2 : 5

(iii) Ratio of boys to the total no of students = 30 : 50
= \(\frac{30}{50}\)
= \(\frac{3}{5}\)
= 3 : 5

Objective Type Questions

Question 7.
The ratio of ₹ 1 to 20 paise is _____
(a) 1 : 5
(b) 1 : 2
(c) 2 : 1
(d) 5 : 1
Solution:
(d) 5 : 1
Hint: ₹ 1 = 100 paise

Question 8.
The ratio of 1 m to 50 cm is
(a) 1 : 50
(b) 50 : 1
(c) 2 : 1
(d) 1 : 2
Solution:
(c) 2 : 1

Question 9.
The length and breadth of a window are 1 m and 70 cm respectively. The ratio of the length to the breadth is
a) 1 : 7
(b) 7 : 1
(c) 7 : 10
(d) 10 : 7
Solution:
(d) 10 : 7

Question 10.
The ratio of the number of sides of a triangle to the number of sides of a rectangle is
(a) 4 : 3
(b) 3 : 4
(c) 3 : 5
(d) 3 : 2
Solution:
(b) 3 : 4

Question 11.
If Azhagan is 50 years old and his son is 10 years old then the simplest ratio between the age of Azhagan to his son is
(a) 10 : 50
(b) 50 : 10
(c) 5 : 1
(d) 1 : 5
Solution:
(c) 5 : 1

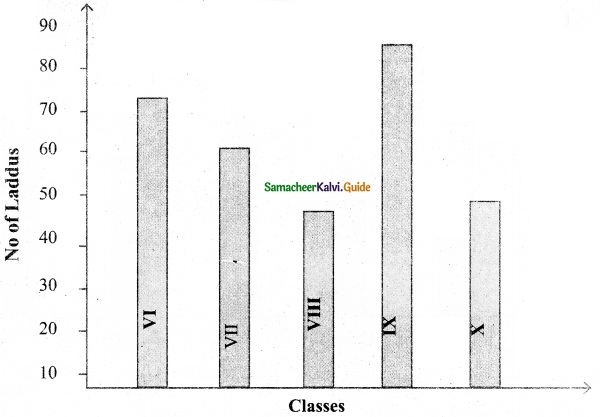
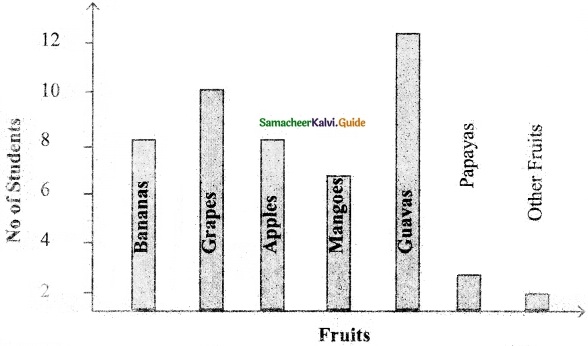
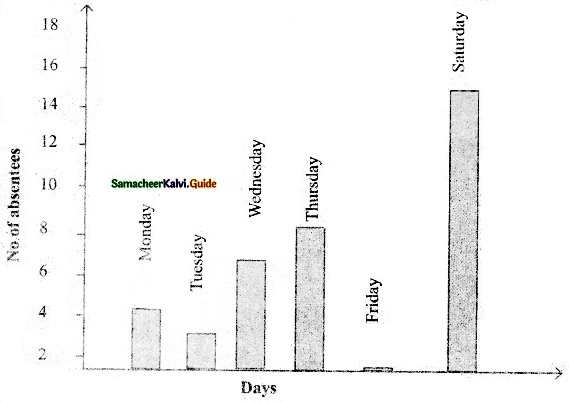
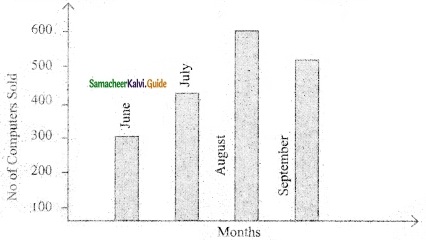
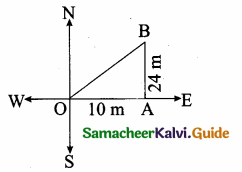
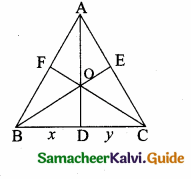
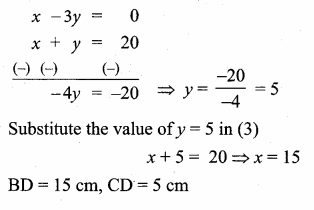
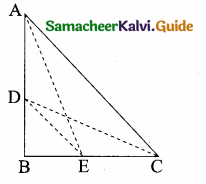
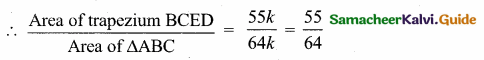
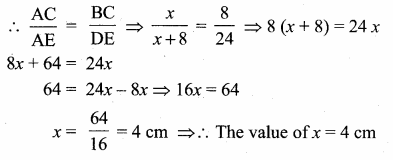
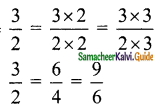
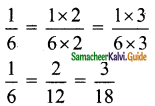
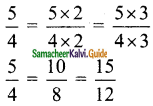
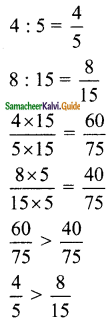
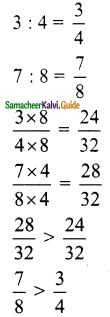
Students can download Maths Chapter 2 Introduction to Algebra Ex 2.3 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 2 Introduction to Algebra Ex 2.3

Miscellaneous Practice Problems

Question 1.
Complete the following pattern.
9 – 1 =
98 – 21 =
987 – 321 =
9876 – 4321 =
98765 – 54321 =
What comes next?
Solution:
9 – 1 = 8
98 – 21 = 77
987 – 321 = 666
9876 – 4321 = 5555
98765 – 54321 = 44444
Next will be 987654 – 654321 = 333333

Question 2.
A piece of wire is ‘12s’ cm long. What will be the length of the side if it is formed as
(i) an equilateral triangle.
(ii) a square?
Solution:
(i) An equilateral triangle has 3 equal sides.
Length of the wire = ‘12s’ cm
Length of each side = \(\frac{12 s}{3}\) cm.
Length of each side of the triangle = 4s cm
(ii) A square has four equal sides.
Length of each side \(\frac{12 s}{4}\) cm
Length of each side of the square 3s cm

Question 3.
Identify the value of the shapes and figures in the table given below and verify their addition horizontally and vertically.

Solution:

Question 4.
The table given below shows the results of the matches played by 8 teams in a kabaddi championship tournament.

Find the value of all the variables in the table given above.
Solution:
k = 3, m = 1, n = 10, a = 9, b = 6, c = 4, x = 4, y = 9

Challenging Problems

Question 5.
Gopal is 8 years younger than Karnan. If the sum of their ages is 30, how old is Karnan?
Solution:
Let the age of Kaman be x years
Gopal’s age = x – 8
Ace to the problem, x + x – 8 = 30
2x – 8 = 30
2x = 30 + 8
2x = 38
x = \(\frac{38}{2}\)
x = 19
Age of Kaman = 19 years

Question 6.
The rectangles made of identical square blocks with varying lengths but having only two square blocks as width are give below

(i) How many small size squares are there in each of the rectangles P,Q, R and S?
(ii) Fill in the boxes.

Solution:
(i) P = 2; Q = 8; R = 6; S = 10

Question 7.
Find the variables from the clues given below and solve the crossword puzzle.


Solution:

Students can download Maths Chapter 5 Statistics Ex 5.3 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 5 Statistics Ex 5.3

Question 1.
Read the given Bar Graph which shows the percentage of marks obtained by Brinda in different subjects in an assessment test.

Observe the Bar Graph and answer the following questions.
(i) 1 Unit = ………… % of marks on vertical line.
(ii) Brinda has scored maximum marks in …….. subject.
(iii) Brinda has scored minimum marks in …….. subject.
(iv) The percentage of marks scored by Brinda in Science is ……..
(v) Brinda scored 60 % marks in the subject ……..
(vi) Brinda scored 20% more in …….. subject than ……… subject.
Solution:
(i) 10
(ii) Mathematics
(iii) Language
(iv) 65%
(v) English
(vi) Mathematics, Science

Question 2.
Chitra has to buv Laddus in order to distribute to her friends as follows:

Draw a Bar Graph for this data.
Solution:
Distribution of Laddus by Chitra to her friends
Scale : 1 unit = 10 Laddus

Question 3.
The fruits liked by the students of a class are as follows:

Solution:
Draw a bar graph for data this data
Scale 1 unit = 2 fruits

Question 4.
The pictograph below gives the number of absentees on different days of the week in class six. Draw the Bar graph for the same.

Solution:
No of absentees on different days of the week in a class
Scale 1 unit = 2 students

Objective Type Questions

Question 5.
A bar graph can be drawn using
(a) Horizontal bars only
(b) Vertical bars only
(c) Both horizontal bars and Vertical bars
(d) Either horizontal bars or vertical bars
Solution:
(d) Either horizontal bars or vertical bars

Question 6.
The spaces between any two bars in a bar graph
(a) can be different
(b) are the same
(c) are not the same
(d) all of these
Solution:
(b) are the same

Students can download Maths Chapter 5 Statistics Ex 5.2 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 5 Statistics Ex 5.2

Question 1.
Fill in the blanks.

(iii) Representation of data by using pictures is known as ………
Solution:
(i) 150
(ii)
(iii) Pictograph

Question 2.
Draw a pictograph for the given data.

(Choose your own suitable scale)
Solution:
Number of computers sold
Scale : 1 Unit = 100 computers

Question 3.
The following table shows the number of tourists who visited the places in the month of May. Draw a pictograph

(Choose your own suitable scale)
Solution:
Number of Tourists who visited the places in the month of May.

Question 4.
The following pictograph shows the number of students playing different games in a school.

Answer the following questions.
(i) Which is the most popular game among the students?
(ii) Find the number of students playing Kabaddi.
(iii) Which two games are played by an equal number of students?
(iv) What is the difference between the number of students playing Kho-Kho and Hockey?
(v) Which is the least popular game among the students?
Solution:
(i) Kabaddi is the most popular game among students.
(ii) There are 11 × 10 = 110 students playing kabaddi.
(iii) Kho-Kho and Hockey are played by an equal number of students.
(iv) Difference is 90 – 90 = 0.
(v) Basketball is the least popular game among students.

Objective Type Questions

Question 5.
The pictorial representation for a phrase is a ____
(a) Picto
(b) Tally mark
(c) Frequency
(d) Data
Solution:
(d) Data

Question 6.
A pictograph is also known as
a) Pictoword
(b) Pictogram
(c) Pictophrase
(d) Pictograph
Solution:
(b) Pictogram

Students can download Maths Chapter 5 Statistics Ex 5.1 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 5 Statistics Ex 5.1

Question 1.
Fill in the blanks.

1. The collected information is called ……..
2. An example of Primary data is ………
3. An example of Secondary Data is ……….
4. The tally marks for number 8 in standard form is ………

Solution:

1. Data
2. List of absentees in a class
3. Cricket scores gathered from a website
4. 

Question 2.
Viji threw a die 30 times and noted down the result each time as follows. Prepare a table on the numbers shown using Tally Marks.
1, 4, 3, 5, 5, 6, 6, 4, 3, 5, 4, 5, 6, 5, 2, 4, 2, 6, 5, 5, 6, 6, 4, 5, 6, 6, 5, 4, 1, 1
Solution:

Question 3.
The following list tells colours liked by 25 students. Prepare a table using Tally Marks.

Solution:

Question 4.
The following are the marks obtained by 30 students in a class test out of 20 in Mathematics subject.

Prepare a table using Tally Marks.

Question 5.
The table shows the number of calls recorded by a Fire Service Station in one year.

Complete the table and answer the following questions.
(i) Which type of call was recorded the most?
(ii) Which type of call was recorded the least?
(iii) How many calls were recorded in all?
(iv How many calls were recorded as False Alarms?
Solution:

(i) The call for “Other Fires” was recorded the most
(ii) The call for “Rescues” was recorded the least
(iii) The total of 35 calls was recorded
(iv) There are 7 calls were recorded as False alarm.

Objective Type Questions

Question 6.
The tally marks for the number 7 in standard form is ………

Solution:
(b)

Question 7.

(a) 5
(b) 8
(c) 9
(d) 10
Solution:
(c) 9

Question 8.
The plural form of ‘datum’ is ____
(a) datum
(b) datums
(c) data
(d) dates
Solution:
(c) data

Students can download Maths Chapter 4 Geometry Additional Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 4 Geometry Additional Questions

I. Multiple choice questions

Question 1.
If a straight line intersects the sides AB and AC of a ∆ABC at D and E respectively and is parallel to BC, then \(\frac { AE }{ AC } \) = …………
(1) \(\frac { AD }{ DB } \)
(2) \(\frac { AD }{ DB } \)
(3) \(\frac { DE }{ BC } \)
(4) \(\frac { AD }{ EC } \)
Answer:
(2) \(\frac { AD }{ DB } \)

Hint:
By BPT theorem,
\(\frac { AE }{ AC } \) = \(\frac { AD }{ AB } \)

Question 2.
In ∆ABC, DE is || to BC, meeting AB and AC at D and E. If AD = 3 cm, DB = 2 cm and AE = 2.7 cm, then AC is equal to ……..
(1) 6.5 cm
(2) 4.5 cm
(3) 3.5 cm
(4) 3.5 cm
Answer:
(2) 4.5 cm
Hint:
By BPT theorem,

\(\frac { AD }{ DB } \) = \(\frac { AE }{ EC } \)
\(\frac { 3 }{ 2 } \) = \(\frac { 2.7 }{ EC } \)
∴ EC = \(\frac{2.7 \times 2}{3}\) = 1.8 CM
AC = AE + EC
= 2.7 + 1.8 = 4.5 cm

Question 3.
In ∆PQR, RS is the bisector of ∠R. If PQ = 6 cm, QR = 8 cm, RP = 4 cm then PS is equal to …………..
(1) 2 cm
(2) 4 cm
(3) 3 cm
(4) 6 cm
Answer:
(2) 2 cm
Hint:

By ABT theorem,
\(\frac { PS }{ SQ } \) = \(\frac { PR }{ QR } \) ⇒ \(\frac { x }{ 6-x } \) = \(\frac { 4 }{ 8 } \)
24 – 4x = 8x ⇒ 24 = 12x
x = 2
PS = 2 cm

Question 4.
In figure, if \(\frac { AB }{ AC } \) = \(\frac { BD }{ DC } \), ∠B = 40° and ∠C = 60°, then ∠BAD = ……………
(1) 30°
(2) 50°
(3) 80°
(4) 40°
Answer:
(4) 40°
Hint:
\(\frac { AB }{ AC } \) = \(\frac { BD }{ DC } \)

AD is the internal bisector of ∠BAC
∠A + ∠B + ∠C = 180°
∠A + 40° + 60° = 180° ⇒ ∠A = 80°
∴ ∠BAC = \(\frac { 80 }{ 2 } \) = 40°

Question 5.
In the figure, the value x is equal to …………
(1) 4.2
(2) 3.2
(3) 0.8
(4) 0.4

Answer:
(2) 3.2
Hint:
By Thales theorem
(DE || BC)
\(\frac { AD }{ BD } \) = \(\frac { AE }{ EC } \)
\(\frac { x }{ 8 } \) = \(\frac { 4 }{ 10 } \) ⇒ x = \(\frac{8 \times 4}{10}\) = 3.2

Question 6.
In triangles ABC and DEF, ∠B = ∠E, ∠C = ∠F, then ………….
(1) \(\frac { AB }{ DE } \) = \(\frac { CA }{ EF } \)
(2) \(\frac { BC }{ EF } \) = \(\frac { AB }{ FD } \)
(3) \(\frac { AB }{ DE } \) = \(\frac { BC }{ EF } \)
(4) \(\frac { CA }{ FD } \) = \(\frac { AB }{ EF } \)
Answer:
(3) \(\frac { AB }{ DE } \) = \(\frac { BC }{ EF } \)
Hint:

Question 7.
From the given figure, identify the wrong statement.

(1) ∆ADB ~ ∆ABC
(2) ∆ABD ~ ∆ABC
(3) ∆BDC ~ ∆ABC
(4) ∆ADB ~ ∆BDC
Answer:
(2) ∆ ABD ~ ∆ ABC

Question 8.
If a vertical stick 12 m long casts a shadow 8 m long on the ground and at the same time a tower casts a shadow 40 m long on the ground, then the height of the tower is …………..
(1) 40 m
(2) 50 m
(3) 75 m
(4) 60 m
Answer:
(4) 60 m
Hint:

\(\frac { AB }{ DE } \) = \(\frac { BC }{ EF } \)
\(\frac { 12 }{ h } \) = \(\frac { 8 }{ 40 } \); h = \(\frac{40 \times 12}{8}\) = 60

Question 9.
The sides of two similar triangles are in the ratio 2:3, then their areas are in the ratio ………….
(1) 9 : 4
(2) 4 : 9
(3) 2 : 3
(4) 3 : 2
Answer:
(2) 4 : 9
Hint:
Ratio of the Area of two similar triangle
= 2² : 3² = 4 : 9
[squares of their corresponding sides]

Question 10.
Triangles ABC and DEF are similar. If their areas are 100 cm² and 49 cm² respectively and BC is 8.2 cm then EF = …………….
(1) 5.47 cm
(2) 5.74 cm
(3) 6.47 cm
(4) 6.74 cm
Answer:
(2) 5.74 cm
Hint:

Question 11.
The perimeters of two similar triangles are 24 cm and 18 cm respectively.
If one side of the first triangle is 8 cm, then the corresponding side of the other triangle is ………
(1) 4 cm
(2) 3 cm
(3) 9 cm
(4) 6 cm
Answer:
(4) 6 cm
Hint:

Question 12.
A point P is 26 cm away from the centre O of a circle and PT is the tangent drawn from P to the circle 10 cm, then OT is equal to …………
(1) 36 cm
(2) 20 cm
(3) 18 cm
(4) 24 cm
Answer:
(4) 24 cm
Hint:

OT² = OP² – PT²
= 26² – 10²
= (26 + 10) (26 – 10)
OT² = 36 × 16
OT = 6 × 4 = 24 cm

Question 13.
In the figure, if ∠PAB = 120° then ∠BPT = ……….

(1) 120°
(2) 30°
(3) 40°
(4) 60°
Answer:
(4) 60°
Hint:
∠BCP + ∠PAB = 180°
(sum of the opposite angles of a cyclic quadrilateral)
∠BCP = 180° – 120° = 60°
∠BPT = 60°
(By tangent chord theorem)

Question 14.
If the tangents PA and PB from an external point P to circle with centre O are inclined to each other at an angle of 40°, then ∠POA = ………………
(1) 70°
(2) 80°
(3) 50°
(4) 60°
Answer:
(1) 70°
Hint:
∠OPA = \(\frac { 40 }{ 2 } \) = 20°
In ∆OAP.
∠POA + ∠OAP + ∠APO = 180°
(sum of the angles of a triangle)

∠POA + 90° + 20° = 180°
∠POA = 180° – 110° = 70°

Question 15.
In the figure, PA and PB are tangents to the circle drawn from an external point P. Also CD is a tangent to the circle at Q. If PA = 8 cm and CQ = 3 cm, then PC is equal to ……….

(1) 11 cm
(2) 5 cm
(3) 24 cm
(4) 38 cm
Answer:
(2) 5 cm
Hint:
PA = PB (tangent of a circle)
PB = 8 cm
PC + BC = 8
PA + QC = (BC = QC tangent)
PC + 3 = 8
∴ PC = 8 cm – 3 cm = 5 cm

Question 16.
∆ABC is a right angled triangle where ∠B = 90° and BD ⊥ AC. If BD = 8 cm, AD = 4 cm, then CD is …………
(1) 24 cm
(2) 16 cm
(3) 32 cm
(4) 8 cm
Answer:
(2) 16 cm
Hint:
∆DCB ~ ∆DBA
\(\frac { DC }{ DB } \) = \(\frac { DB }{ DA } \)

DB² = DC × DA
8² = DC × 4
DC = \(\frac { 64 }{ 4 } \) = 16 cm

Question 17.
The areas of two similar triangles are 16 cm2 and 36 cm2 respectively. If the altitude of the first triangle is 3 cm, then the corresponding altitude of the other triangle is
(1) 6.5 cm
(2) 6 cm
(3) 4 cm
(4) 4.5 cm
Answer:
(4) 4.5 cm
Hint:

Question 18.
The perimeter of two similar triangles ∆ABC and ∆DEF are 36 cm and 24 cm respectively. If DE =10 cm, then AB is …………
(1) 12 cm
(2) 20 cm
(3) 15 cm
(4) 18 cm
Answer:
(3) 15 cm
Hint:
Perimeter of

Question 19.
In the given diagram θ is ………….
(1) 15°
(2) 30°
(3) 45°
(4) 60°

Answer:
(2) 30°
Hint:
∠BAD = 180° – 150° = 30°
= 180° – 150° = 30°
∠DAC = θ = 30°

Question 20.
If AD is the bisector of ∠A then AC is …………

(1) 12
(2) 16
(3) 18
(4) 20
Answer:
(4) 20
Hint. In ∆ABC, AD is the internal bisector of ∠A
\(\frac { BD }{ DC } \) = \(\frac { AB }{ AC } \)
\(\frac { 4 }{ 10 } \) = \(\frac { 8 }{ x } \)
4x = 10 × 8
x = \(\frac{10 \times 8}{4}\) = 20 cm

Question 21.
In ∆ABC and ∆DEF, ∠A = ∠E and ∠B = ∠F. Then AB : AC is ………….
(1) DE : DF
(2) DE : EF
(3) EF : ED
(4) DF : EF
Answer:
(3) EF : ED
Hint:

\(\frac { AB }{ EF } \) = \(\frac { BC }{ FD } \) = \(\frac { AC }{ ED } \)

Question 22.
Two circles of radius 8.2 cm and 3.6 cm touch each other externally, the distance between their centres is ………….
(1) 1.8 cm
(2) 4.1 cm
(3) 4.6 cm
(4) 11.8 cm
Answer:
(4) 11.8 cm
Hint:
Distance between the two centres

= r₁ + r₂
= 8.2 + 3.6
= 11.8 cm

Question 23.
In the given diagram PA and PB are tangents drawn from P to a circle with centre O. ∠OPA = 35° then a and b is …………

(1) a = 30°, b = 60°
(2) a = 35°, b = 55°
(3) a = 40°, b = 50°
(4) a = 45°, b = 45°
Answer:
(2) a = 35°, b = 55°
Hint:
∠OAP = 90° (tangent of the circle)
∠AOP + ∠OPA + ∠PAO = 180°
b + 35° + 90° = 180°
b = 180° – 125°
= 55°
OP is the angle bisector of ∠P
∴ a = 35°

II. Answer the following questions

Question 1.
The image of a man of height 1.8 m, is of length 1.5 cm on the film of a camera. If the film is 3 cm from the lens of the camera, how far is the man from the camera?
Solution:
Let AB be the height of the man, CD be the height of the image of the man of height 1.8 m (180 cm). LM be the distance between man and lens. LN be the distance between Lens and the film.

Given, AB = 1.8 m (180 cm)
CD = 1.5 cm and LN = 3 cm
Consider ∆ LAB and ∆ LCD
∠ALB = ∠DLC (vertically opposite angles)
∠LAB = ∠LDC (alternate angles) (AB || CD)
∴ ∆ LAB ~ ∆ LDC (AA similarity)
∴ \(\frac { AB }{ CD } \) = \(\frac { LM }{ LN } \) ⇒ \(\frac { 180 }{ 1.5 } \) = \(\frac { x }{ 3 } \) ⇒ 1.5x = 180 × 3
x = \(\frac{180 \times 3}{1.5}\) = \(\frac{180 \times 3 \times 10}{15}\)
x = 360 cm (or) 3.6 m
∴ The distance between the man and the camera = 3.6 cm

Question 2.
A girl of height 120 cm is walking away from the base of a lamp-post at a speed of 0. 6 m/sec. If the lamp is 3.6 m above the ground level, then find the length of her shadow after 4 seconds.
Solution:
Let AB be the height of the lamp-post above the ground level.
AB = 3.6 m = 360 cm
Let CD be the height of the girl.
CD = 1.2 m = 120 cm
The distance travelled by the girl in 4 seconds (AC)
= 4 × 0.6 = 2.4m = 240 cm
Consider ∆ECD and ∆EAB
Given (CD || AB)
∠EAB = ∠ECD = 90°
∠E is common

∴ ∆ EAB = ∆ ECD = 90°
\(\frac { AB }{ CD } \) = \(\frac { AE }{ CE } \)
= \(\frac { x+240 }{ x } \) ⇒ 3 = \(\frac { x+240 }{ x } \)
3x = x + 240
2x = 240 ⇒ x = \(\frac { 240 }{ 2 } \) = 120 cm
∴ Lenght of girls shadow after 4 seconds = 120 cm

Question 3.
In ∆ ABC, AB = AC and BC = 6 cm. D is a point on the side AC such that AD = 5 cm and CD = 4 cm. Show that ∆BCD ~ ∆ACB and hence find BD.
Solution:
Given, In ∆ ABC, AB = AC = 9 cm and BC = 6 cm, AD = 5 cm and CD = 4 cm
\(\frac { BC }{ AC } \) = \(\frac { 6 }{ 9 } \) = \(\frac { 2 }{ 3 } \) …..(1)
\(\frac { CD }{ CB } \) = \(\frac { 4 }{ 6 } \) = \(\frac { 2 }{ 3 } \) ……..(2)

From (1) and (2) we get,
\(\frac { BC }{ AC } \) = \(\frac { CD }{ CB } \)
In ∆ BCD and ∆ ACB
∠C = ∠C (common angle)
\(\frac { BC }{ AC } \) = \(\frac { CD }{ CB } \)
∴ ∆ BCD ~ ∆ ACB
\(\frac { BD }{ AB } \) = \(\frac { BC }{ AC } \) ⇒ \(\frac { BD }{ 9 } \) = \(\frac { 6 }{ 9 } \) ⇒ ∴ BD = 6 cm

Question 4.
The lengths of three sides of a triangle ABC are 6 cm, 4 cm and 9 cm. ∆PQR ~ ∆ABC. One of the lengths of sides of APQR is 35 cm. What is the greatest perimeter possible for ∆PQR?
Solution:
Given, ∆ PQR ~ ∆ ABC

Perimeter of ∆ ABC = 6 + 4 + 9 = 19 cm
When the perimeter of ∆ PQR is the greatest only the corresponding side QR must be equal to 35 cm

Question 5.
A man sees the top of a tower in a mirror which is at a distance of 87.6 m from the tower. The mirror is on the ground, facing upward. The man is 0.4 m away from the mirror, and the distance of his eye level from the ground is 1.5 m. How tall is the tower? (The foot of man, the mirror and the foot of the tower lie along a straight line).
Solution:
Let AB and ED be the heights of the man and the tower respectively. Let C be the point of incidence of the tower in the mirror.
In ∆ ABC and ∆ EDC, we have

∠ABC = ∠EDC = 90°
∠BCA = ∠DCE
(angular elevation is same at the same instant, i.e., the angle of incidence and the angle of reflection are same.)
∴ ∆ ABC ~ ∆ EDC (AA similarity criterion)
Thus,
\(\frac { ED }{ AB } \) = \(\frac { DC }{ BC } \) (corresponding sides are proportional)
ED = \(\frac { DC }{ BC } \) × AB = \(\frac { 87.6 }{ 0.4 } \) × 1.5 = 328.5
Hence, the height of the tower is 328.5 m.

Question 6.
In ∆ PQR, given that S is a point on PQ such that ST || QR and \(\frac { PS }{ SQ } \) = \(\frac { 3 }{ 5 } \). If PR = 5.6 cm, then find PT.
Solution:
In ∆ PQR, we have ST || QR and by Thales theorem,
\(\frac { PS }{ SQ } \) = \(\frac { PT }{ TR } \) …….(1)
Let PT = x
Thus, TR = PR – PT = 5.6 – x

From (1), we get PT = TR (\(\frac { PS }{ SQ } \))
x = (5.6 – x) (\(\frac { 3 }{ 5 } \))
5x = 16.8 – 3x
8x = 16.8
x = \(\frac { 16.8 }{ 8 } \) = 2.1
That is PT = 2.1 cm

Question 7.
In a ∆ ABC, D and E are points on the sides AB and AC respectively such that DE || BC. If AD = 4x – 3, BD = 3x – 1, AE = 8x – 7 and EC = 5x – 3, then find the value of x.
Solution:
In ∆ ABC, DE || BC. By BPT theorem. (Thales theorem)
We get \(\frac { AD }{ DB } \) = \(\frac { AE }{ EC } \) ⇒ \(\frac { 4x-3 }{ 3x-1 } \) = \(\frac { 8x-7 }{ 5x-3 } \)

(8x – 7) (3x – 1) = (4x – 3) (5x – 3)
24x² – 8x – 21x + 7 = 20x² – 12x – 15x + 9
24x² – 8x – 21x + 7 = 20x² – 27x + 9
24x² – 29x + 7 – 20x² + 27x – 9 = 0
∴ 4x² – 2x – 2 = 0
÷ 2 ⇒ 2x² – x – 1 = 0
(x – 1) (2x + 1) = 0

x – 1 = 0 (or) 2x + 1 = 0
x = 1 (or) 2x = – 1
x = – \(\frac { 1 }{ 2 } \) ⇒ since, x ≠ – \(\frac { 1 }{ 2 } \)
∴ The value of x = 1

Question 8.
In the figure AC || BD and CE || DF. if OA = 12 cm, AB = 9cm, OC = 8 cm and EF = 4.5 cm, then find FO.
Solution:

In OBD, AC || BD
∴ \(\frac { OA }{ AB } \) = \(\frac { OC }{ CD } \) (By Thales theorem)
\(\frac { 12 }{ 9 } \) = \(\frac { 8 }{ CD } \)
∴ CD = \(\frac{9 \times 8}{12}\) = 6 CM
In ODF, CE || DF
\(\frac { OC }{ CD } \) = \(\frac { OE }{ EF } \) (By Thales theorem)
\(\frac { 8 }{ 6 } \) = \(\frac { OE }{ 4.5 } \) ⇒ OE = \(=\frac{8 \times 4.5}{6}\) = 6 cm
FO = FE + EO = 4.5 + 6 = 10.5 cm
∴ The value of FO = 10.5 cm

Question 9.
Check whether AD is the bisector of ∠A of ∆ABC in each of the following.
(i) AB = 4 cm, AC = 6 cm, BD 1.6 cm, and CD = 2.4 cm.
Solution:
\(\frac { BD }{ DC } \) = \(\frac { 1.6 }{ 2.4 } \) = \(\frac { 16 }{ 24 } \) = \(\frac { 2 }{ 3 } \) …..(1)
\(\frac { AB }{ AC } \) = \(\frac { 4 }{ 6 } \) = \(\frac { 2 }{ 3 } \) ……..(2)
From (1) and (2) we get,

\(\frac { BD }{ DC } \) = \(\frac { AB }{ AC } \)
By the converse of angle bisector theorem we have,
∴ AD is the internal bisector of ∠A

(ii) AB = 6 cm, AC = 8 cm, BD = 1.5 cm and CD = 3 cm
Solution:
\(\frac { BD }{ DC } \) = \(\frac { 1.5 }{ 3 } \) = 0.5 …….(1)
\(\frac { AB }{ AC } \) = \(\frac { 6 }{ 8 } \) = \(\frac { 3 }{ 4 } \) …….(2)

From (1) and (2) we get,
\(\frac { BD }{ DC } \) ≠ \(\frac { AB }{ AC } \)
Hence AD is not the bisector of ∠A.

Question 10.
In a ∆ABC, AD is the internal bisector of ∠A, meeting BC at D. If AB 5.6 cm, AC = 6 cm and DC = 3 cm, find BC.
Solution:
Given, AB = 5.6 cm, AC = 6 cm, DC = 3 cm
Let BD be x
In ∆ ABC, AD is the internal bisector of ∠A.
By Angle bisector theorem, we have,

\(\frac { BD }{ DC } \) = \(\frac { AB }{ AC } \) ⇒ \(\frac { x }{ 3 } \) = \(\frac { 5.6 }{ 6 } \)
x = \(\frac{3 \times 5.6}{6}\) = 2.8 cm
∴ BC = BD + DC = 2.8 + 3 = 5.8 cm
Length of BC = 5.8 cm

Question 11.
In the figure, tangents PA and PB are drawn to a circle with centre O from an external point P. If CD is a tangent to the circle at E and AP = 15 cm, find the perimeter of ∆PCD.
Solution:
We know that the lengths of the two tangents from an exterior point to a circle are equal.
∴ CA = CE, DB = DE and PA = PB
Now, the perimeter of ∆PCD

= PC + CD + DP
= PC + CE + ED + DP
= PC + CA + DB + DP
= PA + PB = 2 PA (PB = PA)
Thus, the perimeter of APCD = 2 × 15 = 30 cm

Question 12.
ABCD is a quadrilateral such that all of its sides touch a circle. If AB = 6 cm, BC = 6.5 cm and CD = 7 cm, then find the length of AD.
Solution:
Let P, Q, R and S be the points where the circle touches the quadrilateral.
We know that the lengths of the two tangents drawn from an exterior point to a circle are equal. Thus, we have,

AP = AS, BP = BQ, CR = CQ and DR = DS
Hence, AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ AB + CD = AD + BC
⇒ AD = AB + CD – BC
= 6 + 7 – 6.5 = 6.5
Thus, AD = 6.5 cm

Question 13.
A man goes 10 m due east and then 24 m due north. Find the distance from the starting point.
Solution:
Let the initial position of the man be “O” and the final position be B.
In the ∆AOB,

OB² = OA² + AB²
OB² = 10² + 24²
= 100 + 576 = 676
OB = \(\sqrt { 676 }\) = 26 m
The man is at a distance of 26 m from the starting point.

Question 14.
Suppose AB, AC and BC have lengths 13, 16 and 20 respectively. If \(\frac { AF }{ FB } \) = \(\frac { 4 }{ 5 } \) and \(\frac { CE }{ EA } \) = \(\frac { 5 }{ 12 } \) Find BD and DC.
Solution:
Given that AB = 13, AC = 16 and BC = 20. Let BD = JC and DC = y.
Using Ceva’s theorem we have

\(\frac { BD }{ DC } \) × \(\frac { CE }{ EA } \) × \(\frac { AF }{ FB } \) = 1 ………(1)
Substitute the given values
\(\frac { x }{ y } \) × \(\frac { 5 }{ 12 } \) × \(\frac { 4 }{ 5 } \) = 1 ⇒ \(\frac { x }{ y } \) × \(\frac { 1 }{ 3 } \) = 1
\(\frac { x }{ y } \) = 3 ⇒ x = 3y
x – 3y = 0 ……(2)
Given BC = 20
x + y = 20 …..(3)
Subtract (2) and (3)

Question 15.
ABC is a right – angled triangle at B. Let D and E be any two points on AB and BC respectively. prove that AE² + CD² = AC² + DE².
Solution:
In the right ∆ ABE right- angled at B.
AE² = AB² + BE² …..(1)
In the right ∆ DBC,CD² = BD² + BC² ………(2)
Adding (1) and (2) we get
AE² + CD² = AB² + BE² + BD² + BC²
= (AB² + BC²) + (BC² + BD²)
AE² + CD² = AC² + DE²
Hence it is proved

[AC² = AB² + BC²]
[DE² = BE² + BD²]

III. Answer the following questions

Question 1.
A point O in the interior of a rectangle ABCD is joined to each of the vertices A, B, C and D. Prove that OA² + OC² = OB² + OD².
Solution:
Given: O is any point inside the rectangle ABCD.
To prove: OA² + OC² = OB² + OD²
Construction: Through “O” draw EF || AB.
Proof: Using Pythagoras theorem

In the right ∆OEA,
∴ OA²= OE² + AE² …(1)
(By Pythagoras theorem)
In the right ∆OFC,
OC² = OF² + FC² …(2)
(By Pythagoras theorem)
OB² = OF² + FB² … (3)
(By Pythagoras theorem)
In the right ∆OED,
OD² = OE² + ED² … (4)
(By Pythagoras theorem)
By adding (3) and (4) we get
OB² + OD² = OF² + FB² + OE² + ED²
= (OE² + FB²) + (OF² + ED²)
= (OE² + EA²) + (OF² + FC²)
[FB = EA and ED = FC]
OB² + OD² = OA² + OC² using (1) and (2)

Question 2.
A lotus is 20 cm above the water surface in a pond and its stem is partly below the water surface. As the wind blew, the stem is pushed aside so that the lotus touched the water 40 cm away from the original position of the stem. How much of the stem was below the water surface originally?
Solution:
Let O be the bottom of the stem immersed in water.
Let B be the lotus, AB be the length of the stem above the water surface
AB = 20 cm
Let OA be the length of the stem below the water surface
Let OA = x cm
Let C be the point where the lotus touches the water surface when the wind blow.
OC = OA + AB
OC = x + 20 cm
In ∆ AOC, OC² = OA² + AC²
(x + 20)² = x² + 40²
x² + 400 + 40x = x² + 1600

40x = 1600 – 400
40x = 1200
x = \(\frac { 1200 }{ 40 } \) = 30 cm
The stem is 30 cm below the water surface.

Question 3.
In the figure, DE || BC and \(\frac { AD }{ BD } \) = \(\frac { 3 }{ 5 } \), calculate the value of

Solution:
(i) Given, DE || BC and \(\frac { AD }{ BD } \) = \(\frac { 3 }{ 5 } \)
Let AD = 3k and BD = 5k; AB = 3k + 5k = 8k
In ∆^le ABC and ∆ADE
∠A = ∠A (common angle)
∠ABC = ∠ADE (corresponding angle)
Since DE || BC
∴ ∆ ABC ~ ∆ ADE

(ii) Let Area of ∆ ADE be 9k and Area of ∆ ABC be 64 k
Area of ∆ BCED = Area of ∆ ABC – Area of ∆ ADE
= 64 k – 9 k
= 55 k

Question 4.
A boy is designing a diamond shaped kite, as shown in the figure where AE = 16 cm, EC = 81 cm. He wants to use a straight cross bar BD. How long should it be?
Solution:
Let in AB be “x”, BE be “z” and BC be “y”
In the right ∆ AEB,
AB² = AE² + BE²
x² = 16² + Z² …….(1)
In the right ∆ BEC,
BC² = EC² + BE²
y² = 81² + z² ……(2)

In the right ∆ ACD,
AC² = AD² + DC²
97² = x² + y² ….(3)
Add (1) and (2) ⇒ x² + y² = 162 + z² + 81² + z²
x² + y² = 2z² + 16² + 81²
97² = 2z² + 16² + 81² (from 3)
9409 = 2z² + 256 + 6561
= 2z² + 6817
2z² = 9409 – 6817 = 2592
z² = \(\frac { 2592 }{ 2 } \) = 1296
z = \(\sqrt { 1296 }\) = 36
∴ Length of cross bar BD = 2 × BE = 2 × 36 = 72 cm

Question 5.
Find the unknown values in each of the following figures. All lengths are given in centimetres (All measures are not in scale)

Solution:
(i) In ∆ ABC and ∆ ADE,
∠A = ∠A (common angle)
∠ABC = ∠ADE (corresponding angle) [BC || DE]
∆ ABC ~ ∆ ADE (By AAA similarity)

In ∆ EAG and ∆ ECF,
∠E || ∠E (common angle)
∠ECF = ∠EAG (corresponding angle)
Given CF || AG
∆ EAG ~ ∆ ECF
\(\frac { EC }{ EA } \) = \(\frac { CF }{ AG } \) ⇒ \(\frac { 8 }{ x+8 } \) = \(\frac { 6 }{ y } \) ⇒ \(\frac { 8 }{ 12 } \) = \(\frac { 6 }{ y } \) (x = 4)
8y = 6 × 12
y = \(\frac{12 \times 6}{8}\) = 9 cm
∴ The value of x = 4 cm and y = 9 cm.

(ii) In ∆ HBC and ∆ HFG,
∠H = ∠H (common angle)
∠HFG = ∠HBC (corresponding angle)
Given FG || BC
\(\frac { HF }{ HB } \) = \(\frac { FG }{ BC } \) ⇒ \(\frac { 4 }{ 10 } \) = \(\frac { x }{ 9 } \) ⇒ 10x = 36
x = 3.6 cm
In ∆ FBD and ∆ FHD,
∠BFD = ∠HFG (vertically opposite angle)
∠FBD = ∠FHG (Alternate angles)
By AA similarity
∆ FBD ~ ∆ FHG
\(\frac { FG }{ FD } \) = \(\frac { FH }{ FB } \) ⇒ \(\frac { x }{ 3+y } \) = \(\frac { 4 }{ 6 } \)
4 (3 + y) = 3.6 × 6
3 + y = \(\frac{3.6 \times 6}{4}\) = 5.4 ⇒ y = 5.4 – 3 = 2.4 cm
In ∆ AEG and ∆ ABC,
∠A = ∠A (common angle)
∠AEG = ∠ABC (corresponding angles)
Given EG || BC
\(\frac { AE }{ AB } \) = \(\frac { EG }{ BC } \)
\(\frac { z }{ z+5 } \) = \(\frac { x+y }{ 9 } \) ⇒ \(\frac { z }{ z+5 } \) = \(\frac { 3.6+2.4 }{ 9 } \)
\(\frac { z }{ z+5 } \) = \(\frac { 6 }{ 9 } \) ⇒ \(\frac { z }{ z+5 } \) = \(\frac { 2 }{ 3 } \)
3z = 2z + 10 ⇒ 3z – 2z = 10 ⇒ z = 10
∴ The values of x = 3.6 cm, y = 2.4 cm and z = 10 cm.

Question 6.
The internal bisector of ∠A of AABC meets BC at D and the external bisector of ∠A meets BC produced at E. Prove that \(\frac { BD }{ BE } \) = \(\frac { CD}{ CE } \)
Solution:
Given: In ∆ ABC, AD is the internal bisector of ∠A meets BC at D. AE is the external bisector of ∠A meets BC produced to E.
To Proof: \(\frac { BD }{ BE } \) = \(\frac { CD }{ CE } \)

Proof: In ∆ ABC, AD is the internal bisector of ∠A.
By ABT theorem we have,
∴ \(\frac { BE }{ CD } \) = \(\frac { AB }{ AC } \) ……….(1)
In ∆ABC, AE is the external bisector of ∠A.
By ABT theorem we have,
∴ \(\frac { BE }{ CE } \) = \(\frac { AB }{ AC } \) ……….(2)
From (1) and (2) we get
\(\frac { BD }{ CD } \) = \(\frac { BE }{ CE } \) ⇒ ∴ \(\frac { BD }{ BE } \) = \(\frac { CD }{ CE } \)

Question 7.
In a quadrilateral ABCD, the bisectors of ∠B and ∠D intersect on AC at E. Prove that \(\frac { AB }{ BC } \) = \(\frac { AD }{ DC } \)
Solution:
Given: ABCD is a quadrilateral. BE is the bisector of ∠B intersecting AC at E, DE is the bisector of ∠D intersecting AC at E.
To proove: \(\frac { AB }{ BC } \) = \(\frac { AD }{ DC } \)
Proof: In ∆ABC, BE is the internal bisector of ∠D.
By Angle bisector theorem we have,
\(\frac { AE }{ EC } \) = \(\frac { AB }{ BC } \) ……..(1)

In ∆ ACD, DE is the internal bisector of ∠C.
By Angle bisector theorem we have,
∴ \(\frac { AE }{ EC } \) = \(\frac { AD }{ DC } \) ……….(2)
From (1) and (2) we get,
\(\frac { AB }{ BC } \) = \(\frac { AD }{ DC } \)

Question 8.
ABCD is a quadrilateral with AB parallel to DC. A line drawn parallel to AB meets AD at P and BC at Q. Prove that \(\frac { AP }{ PD } \) = \(\frac { BQ }{ QC } \)
Solution:
Given: ABCD is a quadrilateral. AB || DC.
The line PQ intersect AD at P and BC at Q

To prove: \(\frac { AP }{ PD } \) = \(\frac { BQ }{ QC } \)
Proof: In the ∆ABC, OQ || AB
By BPT, theorem we have, \(\frac { AO }{ OC } \) = \(\frac { BQ}{ QC } \) ……………(1)
In the ∆ACD, PO || DC
By BPT, theorem we have, \(\frac { AO }{ OC } \) = \(\frac { AP }{ PD } \) ……..(2)
From (1) and (2) we get, \(\frac { AP }{ PD } \) = \(\frac { BQ }{ QC } \)

Question 9.
D is the midpoint of the side BC of AABC. If P and Q are points on AB and on AC such that DP bisects ∠BDA and DQ bisects ∠ADC, then prove that PQ || BC.
Solution:
In ∆ABD,DP is the angle bisector of ∠BDA.
∴ \(\frac { AP }{ PB } \) = \(\frac { AD }{ BD } \) (angle bisector theorem) ……..(1)
In ∆ADC, DQ is the bisector of ∠ADC
∴ \(\frac { AQ }{ QC } \) = \(\frac { AD }{ DC } \) (angle bisector theorem) ……….(2)

But, BD = DC (D is the midpoint of BC)
Now (2) ⇒ ∴ \(\frac { AQ }{ QC } \) = \(\frac { AD }{ BD } \)
From (1) and (3) We get,
∴ \(\frac { AP }{ PB } \) = \(\frac { AQ }{ QC } \)
Thus PQ || BC (converse of thales theorem)

Question 10.
ABCD is a trapezium with AB || DC. The diagonal AC and BD intersect at E. If ∆AED ~ ∆BEC. Prove that AD = BC.
Solution:
By given data ABCD is a trapezium with AB || DC.
In ∆ ECD and ∆ ABE

∠EDC = ∠EBA
∠ECD = ∠EAB
∴ ∆ DEC ~ ∆ BEA by AA – similarity
\(\frac { DE }{ BE } \) = \(\frac { EC }{ EA } \) = \(\frac { DC }{ BA } \)
\(\frac { DE }{ BE } \) = \(\frac { EC }{ EA } \)
\(\frac { DE }{ EC } \) = \(\frac { BE }{ EA } \) ……….(1)

Also given ∆ DEA ~ ∆ CEB
\(\frac { DE }{ CE } \) = \(\frac { EA }{ EB } \) = \(\frac { DA }{ CB } \)
\(\frac { DE }{ CE } \) = \(\frac { EA }{ EB } \) …………(2)
From (1) and (2) we get
\(\frac { BE }{ EA } \) = \(\frac { EA }{ EB } \) ⇒ EB² = EA²
∴ EB = EA
Substitute in (2) we get
\(\frac { EA }{ EA } \) = \(\frac { DA }{ CB } \)
1 = \(\frac { DA }{ CB } \) ⇒ ∴ AD = DC Hence it is proved

Students can download Maths Chapter 3 Ratio and Proportion Ex 3.5 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 3 Ratio and Proportion Ex 3.5

Miscellaneous Practice Problems

Question 1.
The maximum speed of some of the animals are given below:
the Elephant = 20 km/h; the
Lion = 80 km/h;
the Cheetah =100 km/h
Find the following ratios of their speeds in simplified form and find which ratio is the least?
(i) the Elephant and the Lion
(ii) the Lion and the Cheetah
(iii) the Elephant and the Cheetah
Solution:
(i) The Elephant: the Lion
= 20 : 80 = \(\frac{20}{80}\) = \(\frac{1}{4}\) = 1 : 4

(ii) the Lion : the Cheetah
= 80 : 100 = \(\frac{80}{100}\) = \(\frac{4}{5}\) = 4 : 5

(iii) the Elephant: the Cheetah
= 20 : 100 = \(\frac{20}{100}\) = \(\frac{1}{5}\) = 1 : 5
The ratio of Elephant to Cheetah is the least.

Question 2.
A particular high school has 1500 students 50 teachers and 5 administrators. If the school grows to 1800 students and the ratios are maintained, then find the number of teachers and administrators.
Solution:
Administrators : teachers : students = 5 : 50 : 1500 = 1 : 10 : 300
If the school grows to 1800 students then 10 parts = teachers
1 part = administrators
300 parts = 1800
1 part = \(\frac{1800}{300}\) = 6
10 parts = 6 × 10 = 60
So, if the school grows to 1800 students the new ratio is administrators : teachers: students
6 : 60 : 1800

Question 3.
I have a box which has 3 green, 9 blue, 4 yellow, 8 orange coloured cubes in it.
(a) What is the ratio of orange to yellow cubes?
(b) What is the ratio of green to blue cubes?
(c) How many different ratios can be formed, when you compare each colour to any one of the other colours?
Solution:
Number of green cubes = 3
Number of blue cubes = 9
Number of yellow cubes = 4
Number of orange cubes = 8
(a) Ratio of orange to yellow cubes \(\frac{\text { Number of orange cubes }}{\text { Number of yellow cubes }}=\frac{8}{4}=\frac{2}{1}=2: 1\)
Ratio of orange to yellow cubes = 2 : 1
(b) \(\frac{\text { Number of green cubes }}{\text { Number of blue cubes }}=\frac{3}{9}=\frac{1}{3}\)
Ratio of green to blue cubes = 1 : 3
(c) The ratios can be Orange : Yellow, Orange: blue, Orange : green, Yellow : Orange, yellow : blue, yellow : green, blue : green, blue : orange, blue : yellow, green : orange, green : yellow, green : blue. Thus 12 ratios can be formed.

Question 4.
A gets double of what B gets and B gets double of what C gets. Find A : B and B : C and verify whether the result is in proportion or not.
Solution:
Let x be the part owned by C then A : B : C = 2(2x) : 2x : x = 4x : 2x : x
A : B = 4x : 2x = 2 : 1
B : C = 2x : x = 2 : 1
A : B : : B : C. i.e, They are in proportion.

Question 5.
The ingredients required for the preparation of Ragi Kali, a healthy dish of Tamilnadu is given below.

(a) If one cup of ragi flour is used then, what would be the amount of raw rice required?
(b) If 16 cups of water are used, then how much ragi flour should be used?
(c) Which of these ingredients cannot be expressed as a ratio? Why?
Solution:
(i) \(\frac{1}{4}\) cup
(ii) 8 cups
(iii) Ragi flour, Raw rice, and water are in one unit. Sesame oil and salt are in different units. These different units cannot be compared and cannot be expressed as a ratio because the two quantities of a ratio should be in the same unit.

Question 6.
Antony brushes his teeth in the morning and night on all days of the week. Shabeen brushes her teeth only in the morning. What is the ratio of the number of times they brush their teeth in a week?
Solution:
Number of times Antony brushes a day = 2
Number of times Antony brushes a week = 2 × 7 = 14
Number of times Shabeen brushes a day = 1
Number of times Shabeen brushes a week = 1 × 7 = 7
Number of times Antony brushes : Number of times Antony brushes = 14 : 7 = 2 : 1
The required ratio = 2 : 1

Question 7.
Thirumagal’s mother wears a bracelet made of 35 red beads and 30 blue beads. Thirumagal wants to make smaller bracelets using the same two coloured beads in the same ratio. In how many different ways can she make the bracelets?

Solution:
Red : blue = 35 : 30 = 7 : 6
Different ways (i) 7 : 6
(ii) 14 : 12;
(iii) 21 : 18;
(iv) 28 : 24

Question 8.
Team A wins 26 matches out of 52 matches. Team B wins three fourth of 52 matches played. Which team has a better winning record?
Solution:
Team A = \(\frac{26}{52}\) = \(\frac{1}{2}\)
Team B = \(\frac{3}{4}\) × 52 = 39
Team B has a better winning record.

Question 9.
In a school excursion, 6 teachers and 12 students from 6th standard and 9 teachers and 27 students from 7th standard, 4 teachers and 16 students from 8th standard took part. Which class has the least teacher to student ratio?
Solution:
Std VI – teachers: students = 6 : 12 = 1 : 2
Std VII – teachers : students = 9 : 27 = 1 : 3
Std VIII – teachers : students = 4 : 16 = 1 : 4
Std VIII has the least ratio.

Question 10.
Fill the boxes using any set of suitable numbers 6 : ___ : : ___ : 15
Solution:
6 : ……. = …….. : 15
Product of the extremes = 6 × 15 = 90
Set of suitable numbers
1 and 90, 2 and 45, 3 and 30, 5 and 18, 6 and 15

Question 11.
From your school diary, write the ratio of the number of holidays to the number of working days in the current academic year.
Solution:
Number of holidays = 145
Number of working days = 220
Holidays : working days = 145 : 220
= \(\frac{145}{220}\)
= \(\frac{29}{44}\)
= 29 : 44

Question 12.
If the ratio of Green, Yellow and Black balls in a bag is 4 : 3 : 5, then
(a) Which is the most likely ball that you can choose from the bag?
(b) How many balls in total are there in the bag if you have 40 black balls in it?
(c) Find the number of green and yellow balls in the bag.
Solution:
Green : Yellow : Black = 4 : 3 : 5
(i) Blackballs;
(ii) 96 balls (32 + 24 + 40);
(iii) green balls = 32
yellow balls = 24

Students can download Maths Chapter 3 Ratio and Proportion Ex 3.4 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 3 Ratio and Proportion Ex 3.4

Question 1.
Fill in the blanks.
(i) If the cost of 3 pens is Rs 18, then the cost of 5 pens is ……..
(ii) If Karkuzhali earns Rs 1800 in 15 days, then she earns Rs 3000 in …….. days
Solution:
(i) ₹ 30
Hint: \(5 \times \frac{18}{3}\) = 5 × 6 = ₹ 30
(ii) 25 Days
Hint:
\(\frac{1800}{3000}=\frac{15}{x}\)
⇒ x = \(\frac{15 \times 3000}{1800}\) = 25 days

Question 2.
Say True or False.
(i) If the weight of 40 books is 8 kg, then the weight of 15 books is 3 kg.
(ii) A car travels 90 km in 3 hours with constant speed. It will travel 140 km in 5 hours at the same speed.
Solution:
(i) True
Hint: Weight of 1 book = \(\frac{8}{40}=\frac{1}{5} \mathrm{kg}\)
Flence Weight of 15 books = \(\frac{1}{5} \times 15=3 \mathrm{kg}\)
(ii) False
1 hour the car travels = \(\frac{90}{3}\) = 30 km
In 5 hours the car travels = 30 × 5 = 150 km

Question 3.
If a person reads 20 pages of a book in 2 hours, how many pages will he read in 8 hours at the same speed?
Solution:
In 2 hours, pages read = 20
In 1 hour, pages read = \(\frac{20}{2}\) = 10
In 8 hours, pages read = 10 × 8
= 80 pages

Question 4.
The cost of 15 chairs is ₹ 7500. Find the number of such chairs that can be purchased for ₹ 12,000?
Solution:
Cost of 15 chairs = Rs 7500
Cost of 1 chair = Rs \(\frac{7500}{15}\) = Rs 500
Number of chairs that can be purchased for Rs 12000 = \(\frac{12000}{500}\) = 24 chairs

Question 5.
A car covers a distance of 125 km in 5 kg of LP Gas. How much distance will it cover in 3 kg of LP Gas?
Solution:
In 5 kg of LPG gas, distance covered = 125 km
In 1 kg of LPG gas, distance covered = \(\frac{125}{5}\) = 25 km
In 3 kg of LPG gas, distance covered = 3 × 25 km = 75 km

Question 6.
Cholan walks 6 km in 1 hour at a constant speed. Find the distance covered by him in 20 minutes at the same speed.
Solution:
In 1 hour (60 minutes), distance covered = 6 km
In 1 minute, distance covered = \(\frac{6 km}{60 min}\) = \(\frac{6000 m}{60}\) = 100 m
In 20 minutes, distance covered = 20 × 100 m = 2000 m = 2 km

Question 7.
The number of correct answers given by Kaarmugilan and Kavitha in a quiz competition are in the ratio 10 : 11. If they had scored a total of 84 points in the competition, then how many points did Kavitha get?
Solution:
Total points scored = 84 Ratio = 10 : 11
Sum of the ratio = 10 + 11 = 21
21 parts = 84 points
1 part = \(\frac{84}{21}\) = 4 points
Kavitha = 11 parts
Kaarmugilan = 10 parts
Foints scored by Kavitha = 11 parts = 11 × 4 points = 44 points

Question 8.
Karmegam made 54 runs in 9 overs and Asif made 77 runs in 11 overs. Whose run rate is better? (run rate = ratio of runs to overs)
Solution:
Karmegam Runs made in 9 overs = 54
Runs made in 1 over = \(\frac{54}{9}\) = 6 runs
Asif Runs made in 11 overs = 77
Runs made in 1 over = \(\frac{77}{11}\) = 7 runs
∴ Asif’s run rate is better than Karmegam.

Question 9.
You purchase 6 apples for Rs 90 and your friend purchases 5 apples for Rs 70. Whose purchase is better?
Solution:
Myself
Cost of 6 apples = Rs 90
Cost of 1 apple = \(\frac{Rs 90}{6}\) = Rs 15
Friend’s purchase
Cost of 5 apples = Rs 70
Cost of 1 apple = \(\frac{70}{5}\) = Rs 14
∴ Friend’s purchase is better than mine.

Objective Type Questions

Question 10.
If a Barbie doll costs ₹ 90, then the cost of 3 such dolls is ₹ _____
(a) 260
(b) 270
(c) 30
(d) 93
Solution:
(b) 270
Hint:
Cost of 3 dolls = 90 × 3 = ₹ 270

Question 11.
If 8 oranges cost Rs 56, then the cost of 5 oranges is Rs …….
(a) 42
(b) 48
(c) 35
(d) 24
Solution:
(c) 35

Question 12.
If a man walks 2 km in 15 minutes, then he will walk _____ km in 45 minutes.
(a) 10
(b) 8
(c) 6
(d) 12
Solution:
(c) 6
Hint:
1 min he walks = \(\frac{2}{15}\) km
45 min he walks = \(\frac{2}{15}\) × 45 = 6 km.

Students can download Maths Chapter 3 Ratio and Proportion Ex 3.2 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 3 Ratio and Proportion Ex 3.2

Question 1.
Fill in the blanks of the given equivalent ratios.
(i) 3 : 5 = 9 : ……
(ii) 4 : 5 = …… : 10
(iii) 6 : …… = 1 : 2
Solution:
(i) 15
Hint: \(\frac{3}{5}=\frac{3 \times 3}{5 \times 3}=\frac{9}{15}\)
(ii) 8
Hint: \(\frac{4}{5}=\frac{4 \times 2}{5 \times 2}=\frac{8}{10}\)
(iii) 12
Hint: \(\frac{1}{2}=\frac{1 \times 6}{2 \times 6}=\frac{6}{12}\)

Question 2.
Complete the table.

Solution:
(i) 1 feet = 12 inches
3 feet = 3 × 12 inches = 36 inches
72 inches = 6 × 12 inches = 6 feet

(ii) 1 week = 7 days
2 weeks = 2 × 7 days = 14 days
63 days = 9 × 7 days = 9 weeks

Question 3.
Say True or False.
(i) 5 : 7 is equivalent to 21 : 15
(ii) If 40 is divided in the ratio 3 : 2, then the larger part is 24
Solution:
(i) False
Hint: \(\frac{21}{15}=\frac{7}{5}=7: 5\)
(ii) True
Hint: \(\frac{3}{5} \times 40=24\)

Question 4.
Give two equivalent ratios for each of the following.
(i) 3 : 2
(ii) 1 : 6
(iii) 5 : 4
Solution:
(i) 3 : 2

3 : 2 = 6 : 4 = 9 : 6

(ii) 1 : 6

1 : 6 = 2 : 12 = 3 : 18

(iii) 5 : 4

5 : 4 = 10 : 8 = 15 : 12

Question 5.
Which of the two ratios is larger?
(i) 4 : 5 or 8 : 15
(ii) 3 : 4 or 7 : 8
(iii) 1 : 2 or 2 : 1
Solution:
(i) 4 : 5 (or) 8 : 15

4 : 5 > 8 : 15

(ii) 3 : 4 (or) 7 : 8

7 : 8 > 3 : 4

(iii) 1 : 2 (or) 2 : 1
1 : 2 = \(\frac{1}{2}\)
2 : 1 = \(\frac{2}{1}\)
= 2
\(\frac{2}{1}\) > \(\frac{1}{2}\)
2 : 1 > 1 : 2

Question 6.
Divide the numbers given below in the required ratio.
(i) 20 in the ratio 3 : 2
(ii) 27 in the ratio 4 : 5
(iii) 40 in the ratio 6 : 14.
Solution:
(i) Ratio = 3 : 2
Sum of the ratio = 3 + 2 = 5
5 parts = 20
1 part = \(\frac{20}{5}\) = 4
3 parts = 3 × 4 = 12
2 parts = 2 × 4 = 8
20 can be divided in the form as 12, 8.

(ii) Ratio = 4 : 5
Sum of the ratio = 4 + 5 = 9
9 parts = 27
1 part = \(\frac{27}{9}\) = 3
4 parts = 4 × 3 = 12
5 parts = 5 × 3 =15
27 can be divided in the form as 12, 15.

(iii) 40 in the ratio 6 : 14
Ratio = 6 : 14
Sum of the ratio = 6 + 14 = 20
20 parts = 40
1 part = \(\frac{40}{20}\) = 2
6 parts = 2 × 6 = 12
14 parts = 2 × 14 = 28
40 can be divided in the form as 12, 28.

Question 7.
In a family, the amount spent in a month for buying Provisions and Vegetables are in the ratio 3 : 2. If the allotted amount is Rs 4000, then what will be the amount spent for
(i) Provisions and
(ii) Vegetables?
Solution:
Allotted amount = Rs 4000
Ratio = 3 : 2
Sum of the ratio = 3 + 2 = 5
5 parts = Rs 4000
1 part = Rs \(\frac{4000}{5}\) = Rs 800
Provisions : Vegetables = 3 : 2
3 parts = 3 × Rs 800 = Rs 2400
2 parts = 2 × Rs 800 = Rs 1600
Amount spent for provisions = Rs 2400
Amount spent for vegetables = Rs 1600

Question 8.
A line segment 63 cm long is to be divided into two parts in the ratio 3 : 4. Find the length of each part.
Solution:
Total length = 63 cm Ratio = 3 : 4
Sum of the ratio = 3 + 4 = 7
7 parts = 63 cm
1 part = \(\frac{63}{7}\) = 9 cm
3 parts = 3 × 9 cm = 27 cm
4 parts = 4 × 9 cm = 36 cm
∴ 63 cm can be divided into the parts as 27 cm and 36 cm.

Objective Type Questions

Question 9.
If 2 : 3 and 4 : …… are equivalent ratios, then the missing term is
(a) 6
(b) 2
(c) 4
(d) 3
Solution:
(a) 6

Question 10.
An equivalent ratio of 4 : 7 is
(a) 1 : 3
(b) 8 : 15
(c) 14 : 8
(d) 12 : 21
Solution:
(d) 12 : 21

Question 11.
Which is not an equivalent ratio of \(\frac{16}{24}\)?
(a) \(\frac{6}{9}\)
(b) \(\frac{12}{18}\)
(c) \(\frac{10}{15}\)
(d) \(\frac{20}{28}\)
Solution:
(d) \(\frac{20}{28}\)

Question 12.
If Rs 1600 is divided
(a) Rs 480
(b) Rs 800
(c) Rs 1000
(d) Rs 200
Solution:
(c) Rs 1000

Students can download Maths Chapter 4 Geometry Unit Exercise 4 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 4 Geometry Unit Exercise 4

Question 1.
In the figure, if BD ⊥ AC and CE ⊥ AB , prove that
(i) ∆ AEC ~ ∆ADB
(ii) \(\frac { CA }{ AB } \) = \(\frac { CE }{ DB } \)

Solution:
(i) ∠AEC = ∠ADB = 90° ∠A is common By AA – Similarity.
∴ ∆AEC ~ ∆ADB
Since the two triangles are similar

(ii) \(\frac { AE }{ AD } \) = \(\frac { AC }{ AB } \) = \(\frac { EC }{ DB } \)
\(\frac { AC }{ AB } \) = \(\frac { CE }{ DB } \)

Question 2.
In the given figure AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.

Solution:
In the given diagram ∆AEF and ∆ACD
∠AEF = ∠ACD = 90°
∠A is common
By AA – Similarity.
∴ ∆AEF ~ ∆ACD
\(\frac { AE }{ AC } \) = \(\frac { AF }{ AD } \) = \(\frac { EF }{ CD } \)
\(\frac { AE }{ AC } \) = \(\frac { EF }{ CD } \)
\(\frac { AE }{ AC } \) = \(\frac { 4 }{ x } \)
AC = \(\frac{\mathrm{AE} \times x}{4}\) …..(1)
In ∆EAB and ∆ECD,
∠EAB = ∠ECD = 90°
∠E is common
∆ ECD ~ ∆EAB
\(\frac { EC }{ EA } \) = \(\frac { ED }{ EB } \) = \(\frac { CD }{ AB } \)
\(\frac { EC }{ EA } \) = \(\frac { x }{ 6 } \)
EC = \(\frac{\mathrm{EA} \times x}{6}\) …….(2)
In ∆AEB; CD || AB
By Basic Proportionality Theorem
\(\frac { AB }{ CD } \) = \(\frac { EB }{ ED } \)
\(\frac { 6 }{ x } \) = \(\frac { 5+y }{ y } \)
x = \(\frac { 6y }{ y+5 } \) (EC = x) …….(3)
Add (1) and (2) we get
AC + EC = \(\frac{A E \times x}{4}+\frac{x \times E A}{6}\)
>
Substitute the value of x = 2.4 in (3)
2.4 = \(\frac { 6y }{ y+5 } \)
6y = 2.4y + 12
6y – 2.4y = 12 ⇒ 3.6 y = 12
y = \(\frac { 12 }{ 3.6 } \) = \(\frac { 120 }{ 36 } \) = \(\frac { 10 }{ 3 } \) = 3.3 cm
The value of x = \(\frac { 12 }{ 5 } \) (or) 2.4 cm and y = \(\frac { 10 }{ 3 } \) (or) 3.3 cm

Question 3.
O is any point inside a triangle ABC. The bisector of ∠AOB, ∠BOC and ∠COA meet the sides AB, BC and CA in point D, E and F respectively. Show that AD × BE × CF = DB × EC × FA.
Solution:
In ∆ABC the bisector meets AB at D, BC at E and AC at F.

The angle bisector AO, BO and CO intersect at “O”.
By Cevas Theorem
\(\frac { AD }{ DB } \) × \(\frac { BE }{ EC } \) × \(\frac { CF }{ AF } \) = 1
AD × BE × CF = DB × EC × AF
Hence it is proved

Question 4.
In the figure, ABC is a triangle in which AB = AC. Points D and E are points on the side AB and AC respectively such that AD = AE. Show that the points B, C, E and D lie on a same circle.

Solution:
∠B = ∠C (Given AB = AC)
AD + DB = AE + EC
BD = EC (Given AD = AE)
DE parallel BC Since AEC is a straight line.
∠AED + ∠CED = 180°
∠CBD + ∠CED = 180°
Similarly of the opposite angles = 180°
∴ BCED is a cyclic quadrilateral

Question 5.
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of 20 km/hr and the second train travels at 30 km/hr. After 2 hours, what is the distance between them?
Solution:
A is the position of the 1^st train.
B is the position of the 2^nd train.

Distance Covered in 2 hours
OA = 2 × 20 = 40 km
OB = 2 × 30 = 60 km
Distance between the train after 2 hours

Distance between
the two train = 72.11 km (or) 20\(\sqrt { 13 }\) km

Question 6.
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that
(i) b² = p² + ax + \(\frac{a^{2}}{4}\)
(ii) c² = p² – ax + \(\frac{a^{2}}{4}\)
(iii) a² + c² = 2 p² + \(\frac{a^{2}}{2}\)
Solution:
(i) Given ∠AED = 90°

ED = x; DC = \(\frac { a }{ 2 } \)
(D is the mid point of BC)
∴ EC = x + \(\frac { a }{ 2 } \), BE = \(\frac { a }{ 2 } \) – x
∴ In the right ∆ AED
AD² = AE² + ED²
p² = h² + x²
In the right ∆ AEC,
AC² = AE² + EC²

(ii) In the right triangle ABE,
AB² = AE² + BE²
c² = h² + (\(\frac { a }{ 2 } \) – x)²
c² = h² + \(\frac{a^{2}}{4}\) + x² – ax
c² = h² + x² + \(\frac { 1 }{ 4 } \) a² – ax
c² = p² – ax + \(\frac{a^{2}}{4}\) (from 1)

(iii) By adding (2) and (3)
b² + c² = p² + ax + \(\frac{a^{2}}{4}\) + p² – ax + \(\frac{a^{2}}{4}\)
= 2p² + \(\frac{2a^{2}}{4}\)
= 2p² + \(\frac{a^{2}}{2}\)

Question 7.
A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
Solution:
Let the height of the tree AD be “h”.

In ∆ ACD and ∆ BCF,
∠A = ∠B = 90°
∠C is common
∆ ACD ~ ∆ BCF by AA similarity
\(\frac { AD }{ BF } \) = \(\frac { AC }{ BC } \)
\(\frac { h }{ x } \) = \(\frac { 24 }{ 2 } \) = 6
h = 6x ………(1)
In ∆ ACE and ∆ ABF,
∠C = ∠B = 90°
∠A is common
∴ ∆ ACE ~ ∆ ABF
\(\frac { CE }{ BF } \) = \(\frac { AC }{ AB } \)
\(\frac { 2 }{ x } \) = \(\frac { 24 }{ 20 } \)
24x = 20 × 2
x = \(\frac{20 \times 2}{24}=\frac{5 \times 2}{6}=\frac{10}{6}\)
x = \(\frac { 5 }{ 3 } \)
Substitute the value of x in (1)
h = 6 × \(\frac { 5 }{ 3 } \) = 10 m
∴ Height of the tree is 10 m

Question 8.
An emu which is 8 ft tail is standing at the foot of a pillar which is 30 ft high. It walks away from the pillar. The shadow of the emu falls beyond emu. What is the relation between the length of the shadow and the distance from the emu to the pillar?
Solution:
Let the shadow of the emu AE be “x” and BE be “y” ED || BC

By basic proportionality theorem
\(\frac { AE }{ AB } \) = \(\frac { ED }{ BC } \)
\(\frac { x }{ x+y } \) = \(\frac { 8 }{ 30 } \)
30x = 8x + 8y
22x – 8y = 0
(÷ by 2) 11x – 4y = 0
11x = 4y
x = \(\frac { 4 }{ 11 } \) × y
x = \(\frac { 4 }{ 11 } \) × distance from the pillar to emu
Length of = \(\frac { 4 }{ 11 } \) × distance from the shadow the pillar to emu

Question 9.
Two circles intersect at A and B. From a point P on one of the circles lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P.
Solution:
Proof:

A and B are the points intersecting the circles. Join AB.
∠P’PB = ∠PAB (alternate segment theorem)
∠PAB + ∠BAC = 180° …(1)
(PAC is a straight line)
∠BAC + ∠BDC = 180° …(2)
ABDC is a cyclic quadrilateral.
From (1) and (2) we get
∠P’PB = ∠PAB = ∠BDC
P’P and DC are straight lines.
PD is a transversal alternate angles are equal.
∴ P’P || DC.

Question 10.
Let ABC be a triangle and D, E, F are points on the respective sides AB, BC, AC (or their extensions).
Let AD : DB = 5 : 3, BE : EC = 3 : 2 and AC = 21. Find the length of the line segment CF.
Solution:

\(\frac { AD }{ DB } \) = \(\frac { 5 }{ 3 } \); \(\frac { BE }{ EC } \) = \(\frac { 3 }{ 2 } \); AC = 21
By Ceva’s theorem

Length of the line segment CF = 6 units