TN Board 12th Chemistry Important Questions Chapter 7 Chemical Kinetics

Students get through the TN Board 12th Chemistry Important Questions Chapter 7 Chemical Kinetics which is useful for their exam preparation.

TN State Board 12th Chemistry Important Questions Chapter 7 Chemical Kinetics

Answer the following questions.
Question 1.
Express the rate of the following reaction in terms of disappearance of the reactant and appearance or formation of the product: A → B
Answer:
Rate of disappearance of the reactant = \(-\frac{\Delta[\mathrm{A}]}{\Delta t}\)
where the negative sign indicates the concentration of the reactant decreases with time.
Rate of formation of the product = \(+\frac{d[\mathrm{B}]}{d t}\)
The positive sign indicates that the concentration of the product increases with time.

Question 2.
Mention the unit of rate of reaction.
Answer:

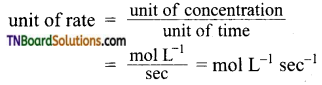
For a gaseous reaction, a unit of rate = atm sec^-1 since concentration is expressed in partial pressures.

Question 3.
Explain how will you determine experimentally determine
(i) average rate of reaction
(ii) instantaneous rate of reaction and
(iii) initial rate of reaction.
Answer:
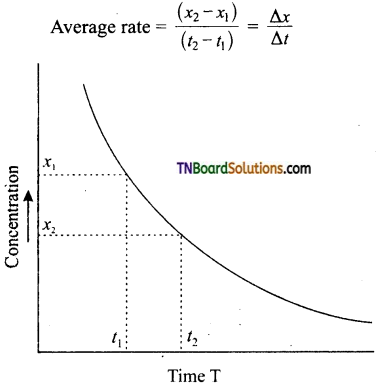
The changes in concentration of the reactants or products are experimentally determined by withdrawing a small portion of the reaction mixture (usually 2 or 5 ml) at suitable intervals of time and then freeze to about 0°C to stop the reaction. The concentration of the reactant or product is measured by a suitable method. A plot of concentration-time is made from the graph, the average rate, instantaneous and initial rates can be determined.
(i) Average rate: Two equivalent points are taken with respect to the time at which the average rate is to be determined. The concentrations corresponding to these points are noted from the graph. The difference in concentration is divided by the time interval between equidistant points. Two equidistant points with respect to T is selected. Let these be ‘t₁,’ and ‘t₂’ respectively. The corresponding concentrations are x₁, and x₂ respectively.

(ii) Instantaneous rate of reaction: For the determination of the instantaneous rate of reaction at any time ‘t’, a tangent is the direction to the curve at the point ‘P’ corresponding to that time. The slope of this tangent gives the instantaneous rate of reaction.

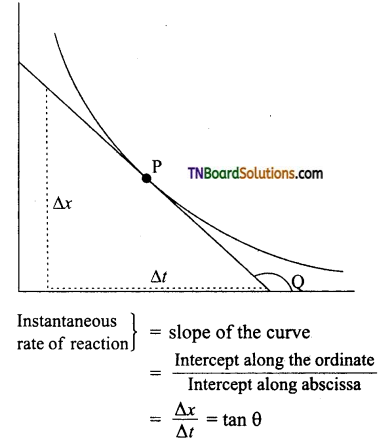
Where Q is the angle of a tangent with the time axis. In a similar manner, the rate of formation of the product can be determined by measuring the slope of the tangent at a particular instant in concentration to the time curve.
(iii) Initial rate of reaction:

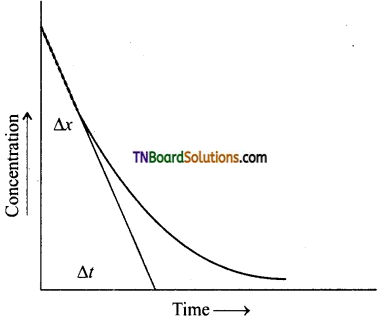
The rate of reaction is maximum at the time of mixing the concentration. This cannot be determined experimentally. This is determined from the concentration is time curve. The curve is extrapolated to zero time and the slope of this curve at zero time gives the initial rate of the reaction.
\(\frac{\Delta x}{\Delta t}\) = initial rate.

Question 4.
In the reaction 2A → products the concentration of A decreases from 0.5 mol L¹ to 0.4 mol L^-1 in 10 minutes. Calculate the rate during this period.
Answer:

Question 5.
The concentration of reactant changes from 0.03 M to 0.02 M in 25 minutes. Calculate the average rate using units of time both in minutes and in seconds.
Answer:

Question 6.
The decomposition of N₂O₅ is expressed by the equation.

If during a certain interval of time the rate of decomposition of N₂O₅ is 1.8 x 10^-3 mol liter 1 min^-1, what will be the rates of formation of NO₂ and O₂ during the same interval.
Answer:
The rate expression for the decomposition of N₂O₅ is

Question 7.
For each of the following reactions, express the given rate of change of concentration of the product or reactant in terms of rate of change of concentration of other reactants or products in that reaction.

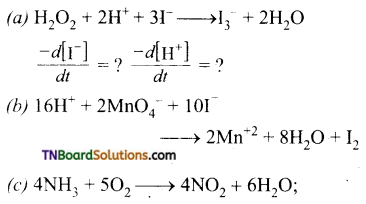
Answer:
(a)

(b) The equality in this case is,


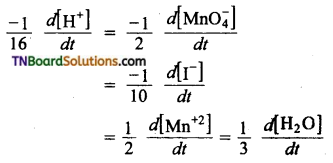
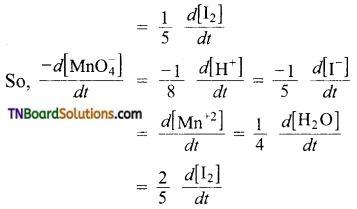
(c) The equality in this case is,

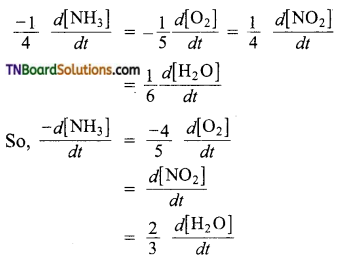
Question 8.
From the concentration of R at different times given below, calculate the average rate of the reaction.
Answer:
R → P during different intervals of time

Average rate of reaction between 0 → 5 sec

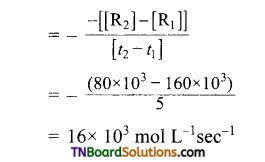
Average-rate of reaction between 5-10 sec

Similarly, average rate between 10 → 20 and 20 → 30 see can be calculated.
Note: What we understand from the above problem is that the rate of reaction is not a constant quantity. It decreases with time.

Question 9.
The decomposition of N₂O₅ is CCl₄ solution at 318K has been studied by monitoring the concentration of the N₂O₅ in the solution. Initially, the concentration of N₂O₅ in the solution is 2.33 M and after 184 minutes it is reduced to 2.08 M. The reaction takes place according to the equation
2N₂O₅ → 4NO₂ + O₂.
Calculate the average rate of the reaction in terms of hours, minutes and seconds. What is the rate of production during this period?
Answer:
Average rate of reaction (mol L^-1 min^-1)

For the given reaction

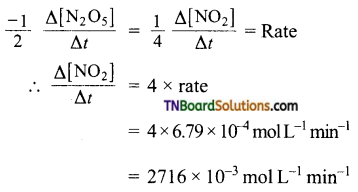
Question 10.
In hydrogenation reaction at 25°C it is observed that hydrogen gas pressure falls from 2 atm to 1.2 atm in 50 min. Calculate the rate of reaction in molarity per sec.
Answer:
R = 0.0821 lit mol^-1 deg^-1

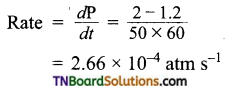
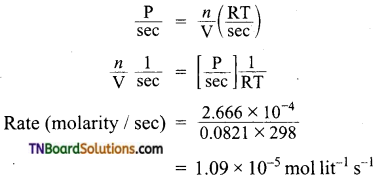
Question 11.
Explain why the average rate cannot be used to produce the rate of reaction at any instant.
Answer:
Because the rate decreases with time as the reaction proceeds. It is not constant.

Question 12.
Bring out the difference between the rate and rate constant of a reaction?
Answer:

Rate of a reaction	The rate constant of a reaction
It represents the speed at which the reactants are converted into products at any instant.	It is a proportionality constant.
It is measured as a decrease in the concentration of the reactants or an increase in the concentration of products.	It is equal to the rate of reaction when the concentration of each of the reactants in unity.
It depends on the initial concentration of reactants.	It does not depend on the initial concentration of reactants.

Question 13.
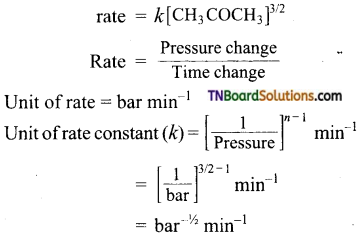
The decomposition of dimethyl ether leads to the formation of CH₄, H_2, and Co and the reaction rate in given by
rate = R [CH₃OCH₃]^3/2
The rate is followed by an increase in pressure in a closed vessel so that the rate is expressed in terms of partial pressure of dimethyl ether.
rate = R[P_CH3OCH3]^3/2
If the pressure is measured in the bar and the time in seconds then what are theTxmts of rate and rate constant?
Answer:
The rate law of the reaction

Question 14.
State the order with respect to each reactant, overall reaction, and the units of the rate constant in each of the following reactions.

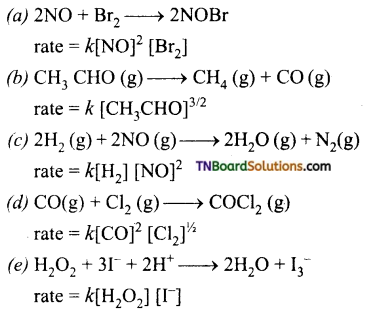
Answer:
(a) Order with respect to NO and Br₂ are 2 and 1 respectively, over all order is 3.

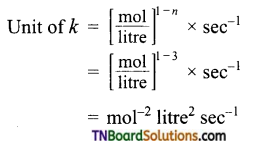
(b) Order \(\frac{3}{2}\)

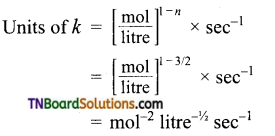
(c) Order with respect to H₂ and NO are 1 and 2 respectively.

= mol^-2 litre² sec^-1
(d) Order with respect to CO and Cl₂ are 2 and \(\frac{1}{2}\) respectively.
Over all order = 2\(\frac{1}{2}\) = \(\frac{5}{2}\)

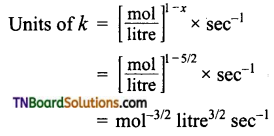
(e) Order with respect to H₂O₂ and I^– are one respectively. Over all order 1 + 1 = 2

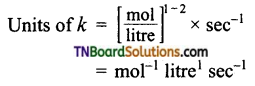
Question 15.
Identify the reaction order from the following rate constants.
(a) k = 3.1 × 10^-4 sec-1
(b) k = 1.12 × 10^-2
(c) k = 1.35 × 10^-2 mol^-2 let² s^-1
(d) k = 3.4 × 10^-3 mol^– let s^-1
Answer:
(a) Let the reaction be of nth order

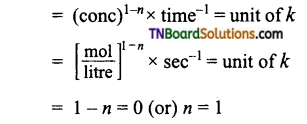
i.e., reaction is of first order.
(b) (atm)^1-n × s^-1 = atm^-1 s^-1
1 – n = -1 : or n = 2
i.e., reaction is of second order.
(c)

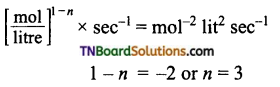
i.e., reaction is of third order.
(d)

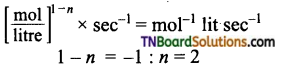
i.e., reaction is of second order.

Question 16.
Derive an expression for the rate constant for the first-order reaction.
Answer:
A reaction whose fate depends on the reactant concentration raised to the first power is called a first order reaction. Let us consider the following Cl₂ first-order reaction,
A → product
Rate law can be expressed as Rate = k [A]¹
Where, k is the first order rate constant.

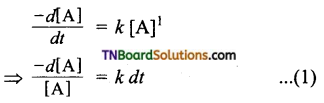
Integrate the above equation between the limits of time t = 0 and time equal to t, while the concentration varies from the initial concentration [A₀] to [A] at the later time.

This equation is in a natural logarithm. To convert it into the usual logarithm with base 10, we have to multiply the term by 2.303.

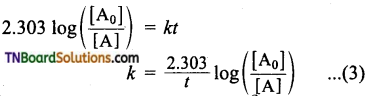
Question 17.
How will you determine the first-order rate constant graphically?
Answer:
For a first order reaction, the rate constant k is given by

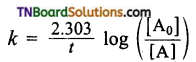
where [A₀] is the initial concentration of the reactant and [A] is the concentration of the reactant at time it\
Rearranging this equation in the form . y = mx + c, we get
log [A₀] – log [A] = \(\frac{kt}{2.303}\)
2.303 [log [A] – log [A]] = kt
log [A₀] – log [A] = \(\frac{k}{2.303}\) t.
Hence a plot of log [A] vs t gives a straight line with a negative slope having the volume of \(\frac{-k}{2.303}\)

Question 18.
Give example for first order reaction.
Answer:
(i) Decomposition of dinitrogen pentoxide
N₂O₅ → (g) 2NO₂ (g) + \(\frac{1}{2}\) O₂ (g)
(ii) Decomposition of thionylchloride;
SO₂Cl₂(l) → SO₂ (g) + Cl₂ (g)
(iii) Decomposition of the H₂O₂ in aqueous solution;
H₂O₂ (aq) → H₂O (l) + \(\frac{1}{2}\) O₂ (g)
(iv) Isomerisation of cyclopropane to propene.

Question 19.
Show that acid hydrolysis of an ester is a pseudo first order reaction.
Answer:
A second order reaction can be altered to a first order reaction by taking one of the reactant in large excess, such reaction is called pseudo first order reaction. Let us consider the acid hydrolysis of an ester,

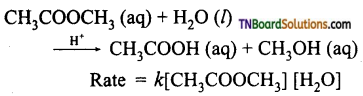
If the reaction is carried out with the large excess of water, there is no significant change in the concentration of water during hydrolysis, i.e., the concentration of water remains almost constant.
Now, we can define k [H₂O] = k’ ; Therefore the above rate equation becomes
Rate = k’ [CH₃COOCH₃]
Thus it follows first-order kinetics.

Question 20.
Give examples of zero-order reactions.
Answer:
(i) Photochemical reaction between H₂ and I₂

(ii) Decomposition of N₂O on a hot platinum surface

(iii) Iodination of acetone in an acid medium is zero-order with respect to iodine.

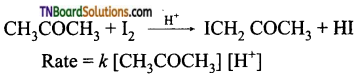
Question 21.
Give the general rate equation for nth-order reaction involving one reactant A.
Answer:
The general rate equation for an nth order reaction involving one reactant [A],
A → product

Consider the case in which n ≠ 1, integration of above equation between [A₀] and [A] at time t = 0 and t = t respectively gives

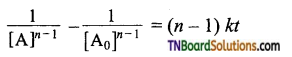
Question 22.
Derive an expression to calculate t_1/2 for a zero-order reaction.
Answer:
Let us calculate the half life period for a zero-order reaction.

The half-life of a zero-order reaction is directly proportional to the initial concentration of the reactant.

Question 23.
Give the general expression for t_1/2 of the nth order (n ≠ 1) reaction.
Answer:
Half-life for an nth order reaction involving reactant A and n ≠ 1

Question 24.
Give the characteristics of first order reaction.
Answer:

1. A change in concentration unit will not change the numerical value of ‘k’
   k = \(\frac{2.303}{t}\) log \(\frac{a}{a-x}\)
   Where ‘a’ and (a – x) are the initial concentration of the reactant and concentration of the reactant at time Y respectively. Thus for the first-order reaction, any quantity which is proportional to the concentration can be used in place of concentration to calculate ‘k’.
2. The time taken for the completion of the same fraction of change is independent of the initial concentration.
3. Time required to calculate nth fraction of reaction t_1/2 can be calculated as When x = \(\frac{a}{n}\) ; t = t_1/n
   Substituting these values in,
   
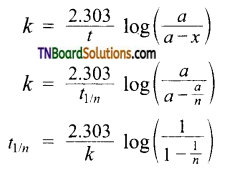
   The above equation can be used to calculate t_3/4 of a reaction.
   
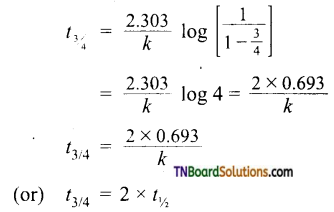
4. In a first-order reaction, the amount of reactant remaining after V half-lives can be calculated as follows:
   where [A₀] – initial concentration of the reactant, [A] = concentration of the reactant remaining after ‘n’ half-lives.

Question 25.
Calculate the half life of a first order reaction from their rate constant given below:
(a) 200 sec^-1 (b) 2 min^-1 (c) 4 year^-1
Answer:

= 3.465 x 10~3 sec
= 0.1732 year.

Question 26.
The rate constant for a first-order reaction is 60 sec^–. How much time will it take to reduce the initial concentration to its 1/16th value?
Answer:

Question 27.
The thermal decomposition of a compound is of the first order. If 50% of the sample is decomposed in 120 minutes, how long will it take for 90% of the compound to decompose?
Answer:
Half life of the reaction = 120 min.
We know that

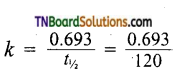
If a= 100, x = 90, a-x = 10
= 5.77 x 10^-3 min^-1
Applying first order rate equation.

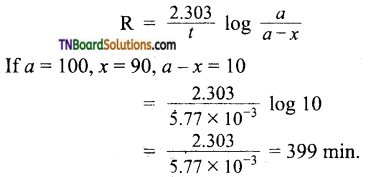
Question 28.
Sucrose decomposes in acid solution into glucose and fructose according to the first-order rate law. With t_1/2 = 3.00 hrs. What fraction of sucrose remains after 8 hours?
Answer:

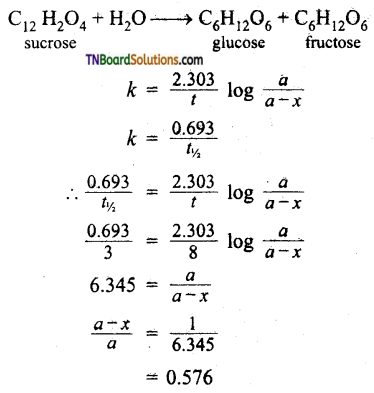
Therefore fraction of reactant remaining = 0.1576

Question 29.
Explain the pressure change method in determining a first-order reaction.
Answer:
If pressure is given in gaseous reactions then we use the following kinetic equation.

where p₀ is the pressure at the initial stage p₀-x is the pressure at time ‘t’ values of p₀ and x can be calculated using the following examples.

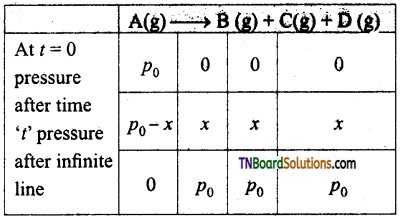
Case I: If total pressure of the reaction mixture is given in place of pressure of reactants.
p_t = (p₀ – x + x + x + x)
Where p_t is the pressure of reaction vessel at time ‘t’.
Case II: If the pressure of the reaction vessel after a long time or infinite time is given
p_t = p₀ + p₀ +p₀

Question 30.
The decomposition of Cl₂O₇ at 400K in the gas phase to Cl₂ and O₂ is a first order reaction.
(i) After 55 seconds at 400K, the pressure of Cl₂O₇ falls from 0.062 to 0.044 atm. Calculate the rate constant.
(ii) Calculate the pressure of Cl₂O₇ after 100 seconds of decomposition at this temperature.
Answer:
(i) As pressure ∝ concentration.

(ii) Applying the first-order rate equation.

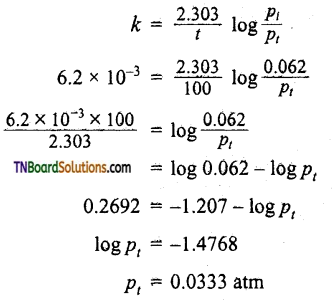
Question 31.
For the decomposition of azo isopropanol to hexane and nitrogen at 543K, the following data are obtained.

t(sec)	p (mm of Hr)
0	35.0
360	54.0
720	63.0

Calculate the rate constant for the reaction.
Answer:
The reaction is

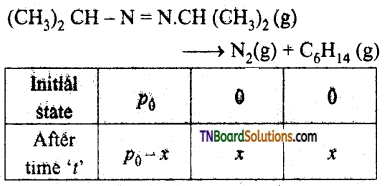
Total pressure – p₀ – x + x + x
p_t = p₀ + x
or x = p_t – p₀
a ∝ p₀
∴ (a – x) ∝ p₀ – (p_t – p₀)
= 2p₀ – p_t
For the first order reaction

Question 32.
Explain Oswald dilution method for determining the order of the reaction.
Answer:
It is applied for these reactions which involve more than one reactant. In this method, the concentration of all reactants are taken in large excess than one. The changes in the concentration of the reactant that is not taken in excess will influence the rate of reaction.
The concentrations of all other reactants practically remain same during the course of reaction. Consider the reaction.
m₁A + m₂B + m₃C → product
Rate = k[A]^α [B]^β [C]^γ
When B and C are taken in excess, the rate law will reduce to
rate = k’ [A]^α
where k’ = k[B]^β [C]^γ
Two sets are taken in which the concentration of A is [A₁] and [A₂] while B and C are present in large excess,
r₁ = [A₁]^α
r₂ = [A₂]^α

From this, the value of α, i.e., the order with respect to A is obtained. The process is repeated one by one and order with respect to others is determined.
Total order of reaction = α + β + γ

Question 33.
Show that if the concentration of a reactant is doubled, the rate of the reaction is also doubled for a first-order reaction, increases four times for a second-order reaction, increases by eight times for a third-order reaction, i.e., A → product.
Answer:
(i) If the concentration of A is doubled.

Hence, for the first-order reaction, if the concentration is doubled, the rate is also doubled.
(ii) For a second-order reaction.

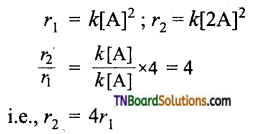
i.e., for a second-order reaction, if the concentration of A is doubled, the rate of the reaction increases by 4 times.
(iii) For a third-order reaction,

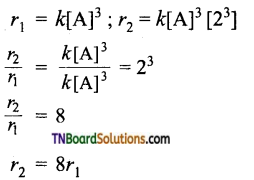
Hence, for a third-order reaction, if the concentration of the reactant is doubled the rate increases 8 times.

Question 34.
Compounds A and B react according to the following chemical equation
A (g) +2B(g) → 2C(g)
Answer:
The concentration of either ‘A’ or ‘B’ was changed keeping the concentration of one of the reactants constant and rates were measured as a function of initial concentration following results were obtained. Find the order with respect to A and B and write the rate law for the reaction

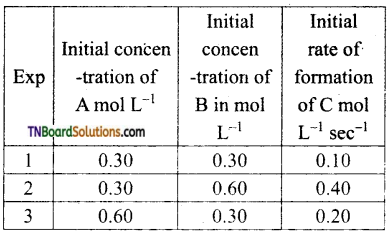
From experiments 1 and 3,
[B] = constant; [A] = doubled
rate is doubled.
Hence rate ∝ [A] i.e., the order with respect to A is 1.
From experiments 1, and 2,
[A] = constant; [B] doubled rate is quadrupled.
Hence, rate ∝ [B]²
i.e., order with respect by B is 2.
Combining rate = k [A] [B]².

Question 35.
The initial rate of reactions
3A + 2B + C → products at different initial concentrations are given below.

Initial rate ms-1	[A0] M	[B0] M	[C0] M
1) 5.0 x 10-3	0.010	0.005	0.010
2) 5.0 x 10-3	0.010	0.005	0.015
3) 1.0 x 10-2	0.010	0.010	0.010
4) 1.25 x 10-3	0.005	0.005	0.010

Answer:
(i) Consider equation (1) and (2)
The concentration of A and B are constant. The rate remains the same for different concentrations of C. Hence, the order with respect to C is zero.
(ii) Consider equations (3) and (1)
The concentration of A and C are constant. The concentration of B is doubled, rate increases by 2 times. Hence order with respect to B is 1.
(iii) Consider equations (4) and (1), The concentration of B and C remain constant. When the concentration of A is doubled, the rate increases by 4 times. Hence order with respect to A is 2.
Alternate method:
Suppose order with respect to A, B and C are α, β and γ respectively. Then the rate law at different concentration of A, B and C are
5.0 × 10^-3 = k [0.010]^α [0.005]^β [0.010]^γ …(1)
5.0 × 10^-3 = k [0.010]^α [0.005]^β [0.015]^γ …(2)
1.0 × 10^-3 = k [0.010]^α [0.010]^β [0.010]^γ …(3)
1.25 × 10^-3 = k [0.005]^α [0.005]^β [0.010]^γ …(4)
Dividing (1) by (2)

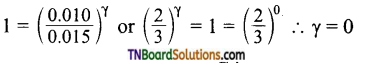
i.e., order with respect to C is zero.
Dividing (3) by (2)

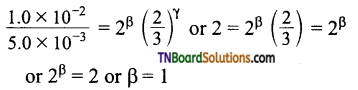
Dividing (1) by (4) ⇒ 4 = 2^α or α = 2
Order with respect to A, B, C are 2, 1 and 0.

Question 36.
A reaction is first order in A and second order in B.
(i) Write the differential rate equation.
(ii) How is the rate affected by increasing the concentration of B, three times, keeping the concentration of A constant?
(iii) How is the rate affected by when the concentration of both A and B are doubled?
Answer:
(i) A + B → product
rate = k [A] [B]²
(ii) If the concentration of B is tripled, the rate increases by 9 times i.e.,

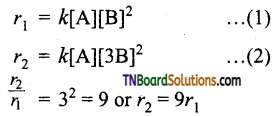
(iii) If the concentration of both A and B are doubled, the rate increases by 8 times.

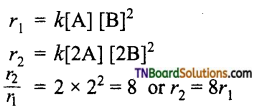
Question 37.
The following rate data were obtained at 303K for the following reaction.
2A + B → C + D.

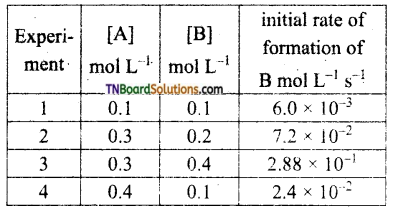
What is the order with respect to each reactant and the overall order of the reaction? write the rate law. Also, calculate the rate constant for the reaction and the units of the rate constant.
Answer:
From experiments 1 and 4, it is seen that [B] the concentration of B is the same but [A] has been made 4 times, the rate of the reaction has also become 4 times. Hence the order with respect to A is 1. i.e., rate ∝ [A],
From experiments 2 and 3, it may be noted that [A] is kept the same but [B] is doubled. The rate of reaction increases by 4 times, i.e., the order with respect to B is 2 combining both,
rate = k[A] [B]². This is the rate law for the reaction.
Alternatively, suppose the order with respect to A is α and the order with respect to B is β, the general rate law for the reaction is
rate = k [A]^α [B]^β
From the data given

Now,

Unit of rate constant (k)

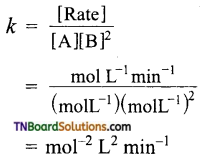
Calculation of rate constant: Substitute the values of α and β in any of the equations.

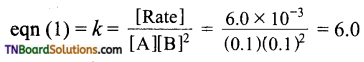
Hence k = 6.0 mol^-1 L² min^-1.

Question 38.
In a reaction between A and B, the initial rate of reaction was measured at a different initial concentration of A and B as given below.

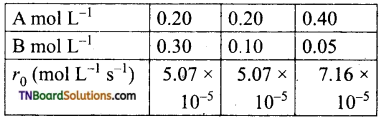
What is the order with respect to A and B?
Answer:
The general rate law is rate = k [A]^α [B]^β where α, β are ordered with respect to A and B respectively.
The given data is


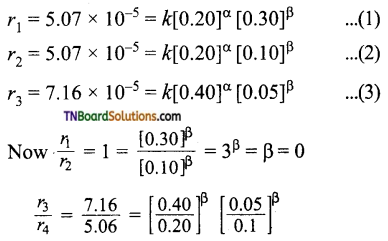
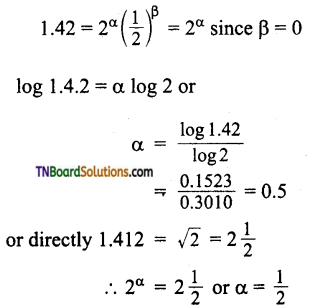
Thus order with respect to A is 0.5 and that of B is 0.

Question 39.
The decomposition of ammonium nitrate in an aqueous solution was studied by placing the apparatus in a thermostat maintained at a particular temperature. The volume of nitrogen gas collected at different intervals of time was as follows:

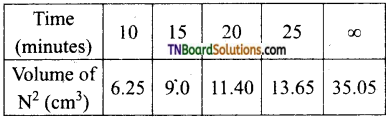
The above data prove that the reaction is of the first order.
Answer:
For a first-order reaction,

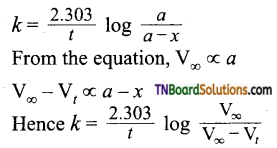
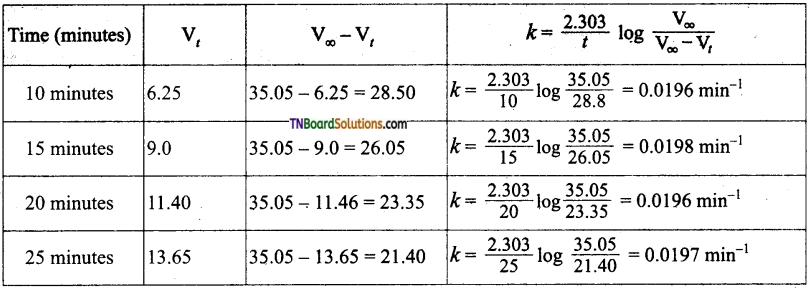
In the present case, V_∞ = 35.05 cm³. The value of R at each instant of time can be calculated as follows:
Values of ‘k’ come nearly constant and hence the reaction is first order.

Question 40.
What do understand by a fraction of effective collisions? Mention its significances.
Answer:
Fraction of effective collisions (f) is given by the following expression

To understand the magnitude of collision factor (f), Let us calculate the collision factor (f ) for a reaction having an activation energy of 100 kJ mol^-1 at 300K.

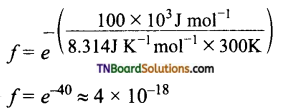
Thus, out of 10¹⁸ collisions, only four collisions are sufficiently energetic to convert reactants to products.

Question 41.
Explain the importance of the proper orientation of molecules in the collision theory.
Answer:
Even if the reactant possesses sufficient activation energy, their collisions need not result in the formation of products. The molecules should orient themselves in such a way that their collision becomes fruit fill. The fraction of effective collisions (f) having orientation is given by steric factor (p). Thus, the rate of reaction is given by
rate = p x f x collision rate
(or) rate = pz\(e^{-\mathrm{E}_{a} / \mathrm{RT}}\)

Question 42.
Define activation energy of a reaction.
Answer:
Activation energy is the extra amount of energy that is supplied from outside so that colloiding molecules must produce effective collisions.

Question 43.
Arrhenius equation is given by k = A\(e^{-\mathrm{E}_{a} / \mathrm{RT}}\). Based on this equation answer the following questions.
(i) Can reactions have zero activation energy?
(ii) Can a reaction have negative activation energy?
Answer:
(i) k = A\(e^{-\mathrm{E}_{a} / \mathrm{RT}}\), when the expression becomes k = e° = A.
The rate constant k = collision frequency. This implies that every collision is an effective collision and leads to product formation which is not possible. Thus activation energy can not be zero.
(ii) When E_a is negative, the above equation

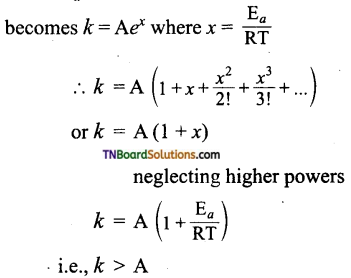
Rate constant having a higher value than collision frequency which is not possible.

Question 44.
Explain the effect of temperature on reaction rate based on Arrhenius’s theory.
Answer:
An increase in temperature increases the fraction of the total number of molecules having the necessary energy of activation which in terms increases the number of effective collisions and hence the rate.

Question 45.
Write Arrhenius equation and explain the terms? What is the significance of frequency factor A in the equation?
Answer:
The Arrhenius equation is k = A\(e^{-\mathrm{E}_{a} / \mathrm{RT}}\) Where ‘k’ is the rate constant for the reaction, A is called the pre-exponential factor, E_a is the energy of activation and R is the gas constant and T is the absolute temperature. The two quantities A and E_a are called the Arrhenius parameters.
The frequency factor gives the frequency of binary collision of the reacting molecules per liter per second. It practically remains constant and does not vary with temperature.

Question 46.
Explain how the energy of activation for a reaction is determined.
Answer:
The rate constant of a reaction is determined at two different temperatures. If R₁ is the rate constant at temperature T₁ arid R₂ is the rate constant at temperature T₂ thereby using a logarithmic form of Arrhenius equation

E_a can be calculated.

Question 47.
Describe how the energy of activation of a reaction is determined graphically.
Answer:
The Arrhenius equation is written in the form,

This equation is of the form y = mx + C i.e., equation for a straight line. Thus, if a plot of log k is \(\frac{1}{T}\) is a straight line, the validity of the equation is confirmed.
Thus the values of k at different temperatures are found and a plot of log k vs \(\frac{1}{T}\) is made.
A straight line with a negative slope is obtained from the value of the slope, E_a can be calculated.
Slope = \(\frac{-\mathrm{E}_{a}}{2.303 \mathrm{R}}\)

Question 48.
The rate constant for a reaction is 1.2 x 10^-3 sec^– at 30°C and 2.1 x 10^-3 sec^-1 at 40°C. Calculate the energy of activation.
Answer:
Given that k₁ = 1.2 x 10^-3 sec^-1
T₁ = 30 + 273 = 303K
k₂ = 2.1 x 10^-3 sec^–
T₂ = 40 + 273 = 313K
Substituting these values in the equation
Solving E_a = 44126.3J = 44.13kJ

Question 49.
The rate of particular reaction doubles when temperature changes from 27°C to 37°C. Calculate the energy of activation.
Answer:
Given that T₁ = 27°C = 273 +21 = 300K
T₂ = 37°C = 273 + 37 = 310K
k₂ = 2k₁
Substituting these values in the equation.
This as solving for E_a
E_a = 53598.6 J mol^-1 or 53.6 kJ mol^-1

Question 50.
The activation energy of a reaction is 94.14 kJ mol^-1 and the value of the rate constant at 313K. is 1.8 x 10^-1 sec^-1 . Calculate the frequency factor (A).
Answer:
Given that, E_a = 94.14 kJ mol^-1 = 9414 J mol^-1
T = 313K,
k = 1.8 x 10^-1 sec^-1 Substituting these values in
= (log 1.8 – 5)+ 15.7082
= (0.2553 – 5)+ 15.708
= 10.963J
A = Anti log (10.963 J)
= 9.194 x 10^-10 sec

Question 51.
The first order rate constant for the decomposition of ethyl iodide by the reaction
C₂H₅I (g) → C₂H₄ (g) + HI (g)
at 600 K is 1.60 x 10^-1 s^-1. Its energy of activation is 209 kJ / mol. Calculate the rate constant of the reaction at 700K.
Answer:
Given T₁ = 600 K
k₁ = 1.60 x 10^-5 sec^-1
T₂ = 700K
k₂ = ?
E_a = 299 kJ mol^-1 = 299000 J mol^-1
Substituting these values in the equation.

Question 52.
Rate constant ‘k’ of a reaction varies with temperature according to the equation
where E_a is the energy of activation for the reaction. When a graph is plotted for log k vs \(\frac{1}{T}\) a straight line with slope – 6670 K is obtained.
Calculate the energy of activation for the reaction and mention is units.
(R = 8.314 J k^-1 mol^-1)
Answer:
Slope of the line = \(\frac{-\mathrm{E}_{a}}{2.303 \mathrm{R}}\) = -6670K
E_a = 2.303 x 8.314 x 6670 = 127711.4 J mol^-1

Choose the correct answers:

1. Which of the following statements is not correct about the order of reaction?
(a) The order of a reaction can be fractional.
(b) Order of reaction is an experimental quantity.
(c) The order of the reaction is always equal to the sum of the stoichiometric coefficients of reactants in a balanced chemical equation for the reaction.
(d) The order of a reaction is the sum of the powers of molar concentrations of the reactants in the rate law expression.
Answer:
(c)

2. Which of the following statements is correct?
(a) The rate of reaction decreases with the passage of time as the concentration of the reactant decreases.
(b) The rate of reaction is the same at any time during the reaction.
(c) The rate of reaction is independent of temperature change.
(d) The rate of reaction decreases with an increase in the concentration of reactants.
Answer:
(a)

3. Which of the following expression is correct for the rate of reaction given below:

Answer:
(c)

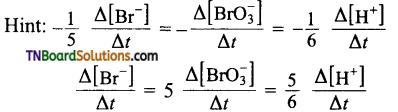
4. Time required for 100 percent completion of a zero-order reaction is:

Answer:
(c)

5. For the reaction aA+ bB → cC,

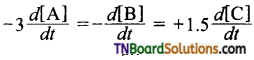
if , then a, b and c respectively are:
(a) 3,1,2
(b) 2,1,3
(c) 1,3,2
(d) 6, 2, 3
Answer:
(c)
Hint: Dividing throughout by 3, we get

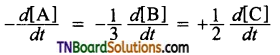
This is so for the reacting A + 3B → 2C

6. The rate of a gaseous reaction is given by the expression k [A] [B]. If the volume of the reaction vessel is suddenly reduced to 1/4th of the initial volume, the reaction rate relating to the original rate will be:
(a) 1/10
(b) 1/8
(c) 8
(d) 16
Answer:
(d)
Hint: Rate = k ab. When volume is reduced to 1/4th, concentrations will become = 4 times.
New rate = k (4a) (4b) = 16 kab = 16 times.

7. In a reaction A → B, the rate of reaction increases two times on increasing the concentration of the reactant four times, then order of reaction is:
(a) 0
(b) 2
(c) 1/2
(d) 4
Answer:
(c)
Hint: (i) r = ka^α, (ii) 2r = k(4a)^α
Dividing (ii) by (i),
4^α = 2 or 2^2α = 2 or 2α = 1 or α = 1/2.

8. The rate of the reaction 2 NO + Cl₂ → 2 NOCl is given by the rate equation: rate = k[NO]²[Cl₂]. The value of the rate constant can be increased by:
(a) increasing the temperature
(b) increasing the concentration of NO
(c) increasing the concentration of Cl₂
(d) doing all of these
Answer:
(a)
Hint: The rate constant of a reaction depends only on temperature and does not depend upon concentrations of the reactants.

9. The unit of rate constant for a zero-order reaction is:
(a) mol L^-1 s^-1
(b) L mol^-1 s^-1
(c) L² mol^-2 s^-1
(d) s^-1
Answer:
(a)

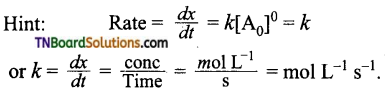
10. Rate constant of a reaction (k) is 175 litre² mol^-2 sec^-1. What is the order of reaction?
(a) first
(b) second
(c) third
(d) zero
Answer:
(c)
Hint: On the basis of given units of k, the reaction is of 3rd order.

11. The reaction A → B follows first order kinetics. The time taken for 0.8 mole of A to produce 0.6 mole of B is 1 hour. What is the time taken for conversion of 0.9 mole of A to produce 0.675 mole of B?
(a) 1 hour
(b) 0.5 hour
(c) 0.25 hour
(d) 2 hours
Answer:
(a)
Hint: The fraction of A reacted in each case is same (0.2 / 0.8 = 1/4),
(0.9 – 0.675)/ 0.90 = 0.225 / 0.90 = 1/4. Hence, time taken is same.

12. 75% of the first-order reaction was completed in 32 min. 50% of the reaction was completed in:
(a) 24 min
(b) 8 min
(c) 16 min
(d) 4 min
Answer:
(c)
Hint: 75 % of reaction is completed in two half-lives, i.e., 2 x t_1/2 = 32 min or t_1/2 = 16 min.

13. 1/[A] vs time is a straight line. The order of the reaction is:
(a) 1
(b) 2
(c) 3
(d) 0
Answer:
(b)
Hint: log [A] vs time is linear for 1st order reactions, 1/[A] vs time is linear for 2nd order reactions; 1/[A]² vs time is linear for 3rd order reactions.

14. If a graph is plotted between in k and 1/T for the first-order reaction, the slope of the straight line so obtained is given by:

Answer:
(a)

15. 10g of a radioactive isotope is reduced to 1.25g in 12 years. Therefore, half-life period of the isotope is:
(a) 24 years
(b) 4 years
(c) 3 years
(d) 8 years
Answer:
(b)

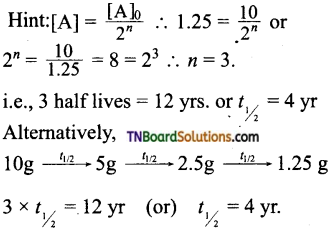
16. The half-life period of a radioactive element is 20 days. What will be the remaining mass of 100 g of it after 60 days?
(a) 25 g
(b) 50 g
(c) 125 g
(d) 20 g
Answer:
(c)
Hint: 60 days = 3 half-lives, i.e, n = 3;

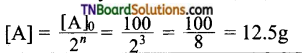
17. Activation energy of a chemical reaction can be determined by:
(a) determining the rate constant at standard temperature.
(b) determining the rate constants at two temperatures.
(c) determining the probability of collision.
(d) using catalyst.
Answer:
(b)
Hint:
Knowing k₁ and k₂ at T₁ and T₂, E_a can be determined. (Arrhenius equation)

18. According to Arrhenius equation, rate constant k is equal to A\(e^{-\mathrm{E}_{a} / \mathrm{RT}}\). Which of the following options represents the graph of k vs \(\frac{1}{T}\)?

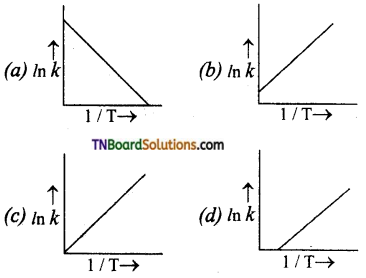
Answer:
(a)
Hint:
k = A\(e^{-\mathrm{E}_{a} / \mathrm{RT}}\). In k = ln A – \(\frac{\mathrm{E}_{a}}{\mathrm{RT}}\). Hence, graph of In k vs \(\frac{1}{T}\) will be linear with negative slope and intercept = ln A.

19. Which of the following statement is incorrect about the collison theory of chemical reaction?
(a) It considers reacting molecules or atoms to be hard spheres and ignores their structural features.
(b) Number of effective collisions determines the rate of reaction.
(c) Collision of atoms or molecules possessing sufficient threshold energy results into the product formation.
(d) Molecules should collide with sufficient threshold energy and proper orientation for the collision to be effective.
Answer:
(c)
Hint: (c) is incorrect because the formation of the product depends not only on energy but also on proper orientation at the time or collision.

20. A first-order reaction is 50% completed in 1.26 x 1014 s. How much time would it take for 100% completion?
(a) 1.26 x 1015 s
(b) 2.52 x 1014 s
(c) 2.52 x 1028 s
(d) infinite
Answer:
(d)
Hint: The whole of the substance never reacts because in every half-life, 50% of the substance reacts. Hence, the time taken for 100% completion of a reaction is infinite.

21. Compounds ‘A’ and ‘B’ react according to the following chemical equation:
A (g) + 2 B(g) → 2C (g)
The concentration of either ‘A’ or ‘B’ was changed keeping the concentrations of one of the reactants constant and rates were measured as a function of initial concentration. Following results were obtained. Choose the correct option for the rate equations for this reaction.

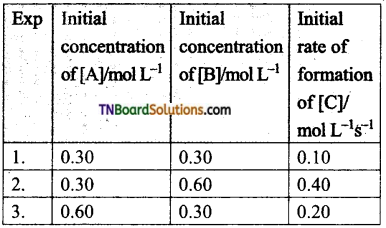
(a) Rate = k [A]² [B]
(b) Rate = k [A] [B]²
(c) Rate = k [A] [B]
(d) Rate = k [A]² [B]⁰
Answer:
(b)
Hint: From expts.l and 3, [B] = constant, [A] = doubled, rate is doubled. Hence, Rate ∝ [A].
From expts. 1 and 2, [A] = constant, [B] = doubled, rate quadrupled. Hence, Rate ∝ [B]².
Combining, Rate = k [A][B]².

22. The rate constant of reaction A → B is 0.6 x 10³ mole per liter per second. If the concentration of A is 5 M, then the concentration of B after 20 minutes is:
(a) 0.36 M
(b) 0.72 M
(c) 1.08M
(d) 3.60 M
Answer:
(b)
Hint: The unit mol L^-1 s^-1 of the rate constant show that it is a reaction of zero order. For a zero order reaction, x = kt. Amount of A reached (x) = (0.6 x 10^-3 mol L^-1 s^-1 ) (20 x 60 s) = 0.72 mol L^-1 [B] formed = [A] reacted = 0.72 mol L^-1

23. The half-life of a substance in a certain enzyme-catalyzed reaction is 138 s. The time required for the concentration of the substance to fall from 1.28 mg L^-1 to 0.04 mg L^-1, is:
(a) 414 s
(b) 552 s
(c) 690 s
(d) 276 s
Answer:
(c)

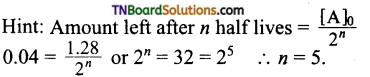
24. The following data is obtained during the first-order thermal decomposition of A (g) → B (g) + C (s) at constant volume and temperature.

S. No.	Time	The total pressure in pascals
1.	At the end of 10 minutes	300
2.	After completion	200

The rate constant in min^-1 is
(a) 0.0693
(b) 6.93
(c) 0.00693
(d) 69.3
Answer:
(a)

25. t_1/4 can be taken as the time taken for the A concentration of a reactant to drop to its initial value. If the rate constant for a first-order reaction is k, then t_1/4 can be written as:
(a) 0.10/k
(b) 029/k
(c) 0.69/k
(d) 0.75/k
Answer:
(b)
Hint:

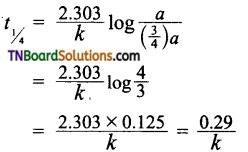
26. A plot of log t_1/2, versus log C₀ is given in the adjoining fig. The conclusion that can be drawn from this graph is:


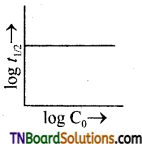
Answer:
(b)

27. In the catalysed decomposition of benzene diazonium chloride,

the half-life period is found to be independent of the initial concentration of the reactant. After 10 minutes, the volume of N₂ gas collected is 10 L and after the reaction is complete, it is 50 L. Hence rate constant of the reaction (in min^-1) is:

Answer:
(b)

28. The activation energy of a reaction can be determined from the slope of which of the following graph?

Answer:
(a)
Hint: From the Arrhenius equation,

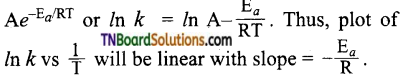
29. The rate of a reaction doubles when its temperature changes from 300 K to 310 K. Activation energy of such a reaction will be:
(a) 60.5 kJ mol^-1
(b) 53.6 kJ mol^-1
(c) 48.6 kJ mol^-1
(d) 58.5 kJ mol^-1
Answer:
(b)

30. In the presence of a catalyst, the activation energy of a reaction is lowered by 2 kcal at 27°C. The rate of reaction will increase by:
(a) 2 times
(b) 14 times
(c) 28 times
(d) 20 times
Answer:
(c)

31. Which one of the following is not correct?
(a) Every bimolecular collision does not result into a chemical reaction.
(b) Collision theory is not applicable to unimolecular reaction.
(c) According to collision frequency, k = PZ_AB \(e^{-\mathrm{E}_{a} / \mathrm{RT}}\) where Z_AB is collision frequency and P is steric factor.
(d) Collision theory assumes molecules to be hard spheres.
Answer:
(b)
Hint: Collision theory is applicable to unimolecular reactions also.