Students can download Maths Chapter 3 Algebra Ex 3.13 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.13
Question 1.
Solve by cross-multiplication method.
(i) 8x – 3y = 12; 5x = 2y + 7
Solution:
8x – 3y – 12 = 0 → (1)
5x – 2y – 7 = 0 → (2)
Use the coefficients for cross multiplication
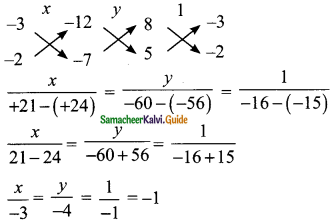
\(\frac{x}{-3}\) = -1 ⇒ x = 3
\(\frac{y}{-4}\) = -1 ⇒ y = 4
∴ The value of x = 3 and y = 4
![]()
(ii) 6x + 7y – 11 = 0; 5x + 2y = 13
Solution:
6x + 7y – 11 = 0 → (1)
5x + 2y = 13 → (2)
Use the coefficient for cross multiplication
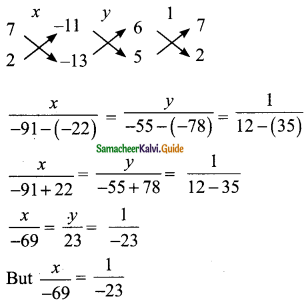
-23x = -69
∴ 23x = 69
x= \(\frac{69}{23}\)
= 3
\(\frac{y}{23}\) = \(\frac{1}{-23}\)
-23y = 23
23y = -23
y = –\(\frac{23}{23}\)
y = -1
∴ The value of x = 3 and y = -1
![]()
(iii) \(\frac{2}{x}\) + \(\frac{3}{y}\) =5; \(\frac{3}{x}\) – \(\frac{1}{y}\) + 9 = 0
Solution:
\(\frac{1}{x}\) = a; \(\frac{1}{y}\) = b
2a + 3b – 5 = 0 → (1)
3a – b + 9 = 0 → (2)
Using the coefficients for cross multiplication
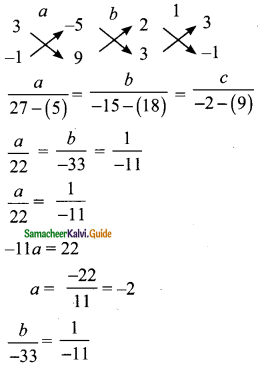
-11b = -33
11b = 33
b = \(\frac{33}{11}\) = 3
But \(\frac{1}{x}\) = a ⇒ \(\frac{1}{x}\) = -2
-2x = 1 ⇒ 2x = -1
x = –\(\frac{1}{2}\)
but \(\frac{1}{y}\) = b
\(\frac{1}{y}\) = 3 ⇒ 3y = 1
y = \(\frac{1}{3}\)
∴ The value of x = –\(\frac{1}{2}\) and y = \(\frac{1}{3}\)
![]()
Question 2.
Akshaya has 2 rupee coins and 5 rupee coins in her purse. If in all she has 80 coins totalling Rs 220, how many coins of each kind does she have.
Solution:
Let the number of 2 rupee coins be “x” and the number of 5 rupee coins be “y”.
By the given first condition
x + y = 80 → (1)
Again by the given second condition
2x + 5y = 220 → (2)
x + y – 80 = 0 → (3)
2x + 5y – 220 = 0 → (4)
Using the coefficients for cross multiplication
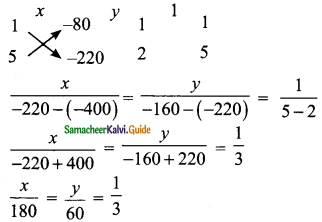
\(\frac{x}{180}\) = \(\frac{1}{3}\)
3x = 180
x = \(\frac{180}{3}\)
= 60
But \(\frac{y}{60}\) = \(\frac{1}{3}\)
3y = 60
y = \(\frac{6}{30}\)
= 20
Number of 2 rupee coins = 60
Number of 5 rupee coins = 20
![]()
Question 3.
It takes 24 hours to fill a swimming pool using two pipes. If the pipe of larger diameter is used for 8 hours and the pipe of the smaller diameter is used for 18 hours. Only half of the pool is filled. How long would each pipe take to fill the swimming pool.
Solution:
Let the time taken by the larger diameter pipe be “x” hours and the time taken by the smaller diameter pipe be “y” hours.
By the given first condition
\(\frac{1}{x}\) + \(\frac{1}{y}\) = \(\frac{1}{24}\) → (1)
Also
In 8 hours the large pipe fill \(\frac{8}{x}\)
In 18 hours the smaller pipe fill \(\frac{18}{y}\)
By the given second condition ( \(\frac{1}{2}\) of the tank)
\(\frac{8}{x}\) + \(\frac{18}{y}\) = \(\frac{1}{2}\) → (2)
Solve (1) and (2) we get
Let \(\frac{1}{x}\) = a; \(\frac{1}{y}\) = b
a + b = \(\frac{1}{24}\)
Multiply by 24
24a + 24b = 1
24a + 24b – 1 = 0 → (3)
8a + 18b = \(\frac{1}{2}\)
Multiply by 2
16a + 36b = 1
16a + 36b – 1 = 0 → (4)

x = 40
\(\frac{1}{y}\) = b ⇒ \(\frac{1}{y}\) = \(\frac{1}{60}\)
y = 60
To fill the remaining half of the pool.
Time taken by larger pipe = \(\frac{1}{2}\) × 40 = 20 hours
Time taken by smaller pipe = \(\frac{1}{2}\) × 60 = 30 hours
![]()