Students can download Maths Chapter 2 Real Numbers Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Additional Questions
I. Multiple choice question
Question 1.
The decimal form of –\(\frac{3}{4}\) is ………
(a) – 0.75
(b) – 0.50
(c) – 0.25
(d) – 0.125
Solution:
(a) – 0.75
![]()
Question 2.
If a number has a non-terminating and non-recurring decimal expansion, then it is……….
(a) a rational number
(b) a natural number
(c) an irrational number
(d) an integer
Solution:
(c) an irrational number
Question 3.
Which one of the following has terminating decimal expansion?
(a) \(\frac{7}{9}\)
(b) \(\frac{8}{15}\)
(c) \(\frac{1}{12}\)
(d) \(\frac{5}{32}\)
Solution:
(d) \(\frac{5}{32}\)
Question 4.
Which of the following are irrational numbers?
(i) \(\sqrt{2+\sqrt3}\)
(ii) \(\sqrt{4+\sqrt25}\)
(iii) \(\sqrt[3]{5+\sqrt7}\)
(iv) \(\sqrt{8-\sqrt[3]8}\)
(a) (ii), (iii) and (iv)
(b) (i), (iii) and (iv)
(c) (i), (ii) and (iii)
(d) (i), (iii) and (iv)
Solution:
(d) (i), (iii) and (iv)
![]()
Question 5.
Irrational number has a
(a) terminating decimal
(b) no decimal part
(c) non-terminating and recurring decimal
(d) non-terminating and non-recurring decimal
Solution:
(d) non-terminating and non-recurring decimal
Question 6.
If \(\frac{1}{7}\) = 0.142857, then the value of \(\frac{3}{7}\) is……..
(a) 0.285741
(b) 0.428571
(c) 0.285714
(d) 0.574128
Solution:
(b) 0.428571
Question 7.
Which of the following are not rational numbers?
(a) 7√5
(b) \(\frac{7}{\sqrt{5}}\)
(c) \(\sqrt{36}\) – 9
(d) π + 2
Solution:
(c) \(\sqrt{36}\) – 9
![]()
Question 8.
The product of 2√5 and 6√5 is……….
(a) 12√5
(b) 60
(c) 40
(d) 8√5
Solution:
(b) 60
Question 9.
The rational number lying between \(\frac{1}{5}\) and \(\frac{1}{2}\)
(a) \(\frac{7}{20}\)
(b) \(\frac{2}{10}\)
(c) \(\frac{2}{7}\)
(d) \(\frac{3}{10}\)
Solution:
(a) \(\frac{7}{20}\)
Question 10.
The value of 0.03 + 0.03 is ……….
(a) 0.\(\overline { 09 }\)
(b) 0.\(\overline { 0303 }\)
(c) 0.\(\overline { 06 }\)
(d) 0
Solution:
(c) 0.06
![]()
Question 11.
The sum of \(\sqrt{343}\) + \(\sqrt{567}\) is
(a) 18√3
(b) 16√7
(c) 15√3
(d) 14√7
Solution:
(b) 16√7
Question 12.
If \(\sqrt{363}\) = x√3 then x = ………
(a) 8
(b) 9
(c) 10
(d) 11
Solution:
(d) 11
Question 13.
The rationalising factor of \(\frac{1}{\sqrt{7}}\) is ……….
(i) 7
(b) √7
(c) \(\frac{1}{7}\)
(d) \(\frac{1}{\sqrt{7}}\)
Solution:
(b) √7
![]()
Question 14.
The value of \((\frac{1}{3^5})^4\) is ……..
(a) 320
(b) 3-20
(c) \(\frac{1}{3^{-20}}\)
(d) \(\frac{1}{3^{9}}\)
Solution:
(b) 3-20
Question 15.
What is 3.976 × 10-4 written in decimal form?
(a) 0.003976
(b) 0.0003976
(c) 39760
(d) 0.03976
Solution:
(b) 0.0003976
II. Answer the following Questions.
Question 1.
Find any seven rational numbers between \(\frac{5}{8}\) and –\(\frac{5}{6}\)
Solution:
Let us convert the given rational numbers having the same denominators.
L.C.M of 8 and 6 is 24.
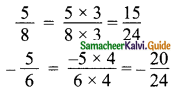
Now the rational numbers between
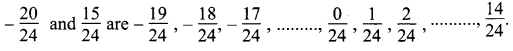
We can take any seven of them.

Question 2.
Find any three rational numbers between \(\frac{1}{2}\) and \(\frac{1}{5}\)
Solution:

Thus the three rational numbers are \(\frac{7}{20}\), \(\frac{17}{40}\) and \(\frac{37}{80}\)
![]()
Question 3.
Represent \(-\frac{2}{11}\), \(-\frac{5}{11}\) and \(-\frac{9}{11}\) on the number lines.
Solution:

To Represent \(-\frac{2}{11}\), \(-\frac{5}{11}\) and \(-\frac{9}{11}\) on the number line we make 11 markings each being equal distence \(\frac{1}{11}\) on the left of 0.
The point A represent \((-\frac{2}{11})\), the point B represents \((-\frac{5}{11})\) and the point C represents \((-\frac{9}{11})\)
Question 4.
Express the following in the form \(\frac{p}{q}\), where p and q are integers and q ≠ 0.
(i) 0.\(\overline { 47 }\)
Solution:
Let x = 0.474747…….. →(1)
100 x = 47.4747…….. →(2)
(2) – (1) ⇒ 100x – x = 47.4747……..
(-) 0.4747……..
99 x = 47.0000
x = \(\frac{47}{99}\)
∴ 0.\(\overline { 47 }\) = \(\frac{47}{99}\)
(ii) 0.\(\overline { 57 }\)
Solution:
Let x = 0.57777…….. →(1)
10 x = 5.77777…….. →(2)
100 x = 57.7777…….. →(3)
(3) – (2) ⇒ 100 x – 10 x = 57.7777……..
(-) 5.7777……..
99 x = 52.0000
x = \(\frac{52}{90}\) = \(\frac{26}{45}\)
∴ 0.\(\overline { 57 }\) = \(\frac{26}{45}\)
(iii) 0.\(\overline { 245 }\)
Solution:
Let x = 0.2454545…….. →(1)
10 x = 2.454545…….. →(2)
1000 x = 245.4545…….. →(3)
(3) – (2) ⇒ 1000 x – 10 x = 245.4545
(-) 2.4545………
990 x = 243.00000
x = \(\frac{243}{990}\) (or) \(\frac{27}{110}\)
∴ 0.\(\overline { 245 }\) = \(\frac{27}{110}\)
![]()
Question 5.
Without actual division classify the decimal expansion of the following numbers as terminating or non-terminating and recurring.
(i) \(\frac{7}{16}\)
(ii) \(\frac{13}{150}\)
(ii) –\(\frac{11}{75}\)
(iv) \(\frac{17}{200}\)
Solution:
(i) \(\frac{7}{16}\) = \(\frac{7}{2^4}\) = \(\frac{7}{2^{4} \times 5^{0}}\)
∴ \(\frac{7}{16}\) has a terminating decimal expansion.
(ii) \(\frac{13}{150}=\frac{13}{2 \times 3 \times 5^{2}}\)
Since it is not in the form of \(\frac{P}{2^{m} \times 5^{n}}\)
∴ \(\frac{13}{150}\) as non-terminating and recurring decimal expansion.
(iii) \(-\frac{11}{75}=-\frac{11}{3 \times 5^{2}}\)
Since it is not in the form of \(\frac{P}{2^{m} \times 5^{n}}\)
∴ –\(\frac{11}{75}\) as non-terminating and recurring decimal expansion.
(iv) \(\frac{17}{200}=\frac{17}{2^{3} \times 5^{2}}\)
∴ \(\frac{17}{200}\) has a terminating decimal expansion.
![]()
Question 6.
Find the value of \(\sqrt{27}\) + \(\sqrt{75}\) – \(\sqrt{108}\) + \(\sqrt{48}\)
Solution:
![]()
= 3√3 + 5√3 – 6√3 + 4√3
= 12√3 – 6√3
= 6√3
= 6 × 1.732
= 10.392
Question 7.
Evaluate \(\frac{\sqrt{2}+1}{\sqrt{2-1}}\)
Solution:
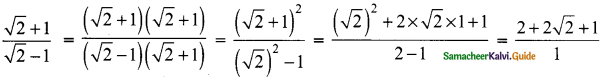
= 2√2 + 3
= 2 × 1.414 + 3
= 2.828 + 3
= 5.828
![]()
Question 8.
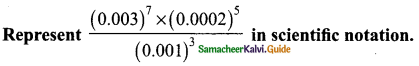
Solution:
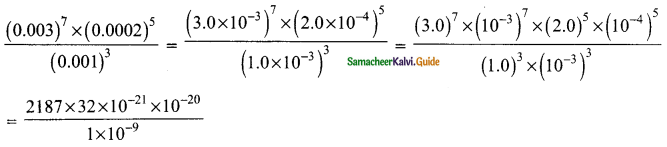
= 69984 × 1021-21-20+9
= 69984 × 10-32
= 6.9984 × 104 × 10-32
= 6.9984 × 10-32+4
= 6.9984 × 10-28
Question 9.
Write
(a) 9.87 × 109
(b) 4.134 × 10-4 and
(c) 1.432 × 10-9 in decimal form.
Solution:
(a) 9.87 × 109 = 9870000000
(b) 4.134 × 10-4 = 0.0004134
(c) 1.432 × 10-9 = 0.000000001432
![]()