Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra Ex 3.6 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 3.6
Question 1.
Fill in the blanks:
(i) The value of x in the equation x + 5 = 12 is ________ .
Answer:
7
Hint:
Given, x + 5 = 12
x = 12 – 5 = 7 (by transposition method)
Value of x is 7
![]()
(ii) The value of y in the equation y – 9 = (-5) + 7 is ________ .
Answer:
11
Hint:
Given, y – 9 = (-5) + 7
y – 9 = 7 – 5 (re-arranging)
y – 9 = 2
∴ y = 2 + 9 = 11 (by transposition method)
(iii) The value of m in the equation 8m = 56 is ________ .
Answer:
7
Hint:
Given, 8m = 56
Divided by 8 on both sides
\(\frac{8 \times m}{8}=\frac{56}{8}\)
∴ m = 7
![]()
(iv) The value of p in the equation \(\frac{2 p}{3}\) = 10 is ________ .
Answer:
15
Hint:
Given, \(\frac{2 p}{3}\) = 10
Multiplying by 3 on both sides
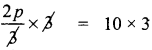
Dividing by 2 on both sides
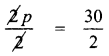
∴ p = 15
(v) The linear equation in one variable has ________ solution.
Answer:
one
Question 2.
Say True or False.
(i) The shifting of a number from one side of an equation to other is called transposition.
Answer:
True
(ii) Linear equation in one variable has only one variable with power 2.
Answer:
False
[Linear equation in one variable has only one variable with power one – correct statement]
![]()
Question 3.
Match the following

(A) (i),(ii), (iv) ,(iii),(v)
(B) (iii), (iv), (i) ,(ii), (v)
(C) (iii),(i) ,(iv), (v), (ii)
(D) (iii) , (i) , (v) ,(iv) ,(ii)
Answer:
(C) (iii),(i) ,(iv), (v), (ii)
a. \(\frac{x}{2}\) = 10, multiplying by 2 on both sides, we get
\(\frac{x}{2}\) × 2 = 10 × 2 ⇒ x = 20
b. 20 = 6x – 4 by transposition ⇒ 20 + 4 =6x
6x = 24 dividing by 6 on both sides,
\(\frac{6 x}{6}=\frac{24}{6}\) ⇒ x = 4
c. 2x – 5 = 3 – x
By transposing the variable ‘x’, we get
2x – 5 + x = 3
by transposing – 5 to other side,
2x + x = 3 + 5
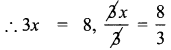
∴ x = \(\frac{8}{3}\)
d. 7x – 4 – 8x = 20
by transposing – 4 to other side,
7x – 8x = 20 + 4
– x = 24
∴ x = – 24
e. \(\frac{4}{11}-x=\frac{-7}{11}\)
Transposing \(\frac{4}{11}\) to other side,
– x = \(\frac{-7}{11} \frac{-4}{11}=\frac{-7-4}{11}=\frac{-11}{11}\) = – 1
∴ – x = – 1 ⇒ x = 1
![]()
Question 4.
Find x:
(i) \(\frac{2 x}{3}-4=\frac{10}{3}\)
Answer:
Transposing – 4 to other side, it becomes + 4

(ii) \(y+\frac{1}{6}-3 y=\frac{2}{3}\)
Answer:
Transposing \(\) to the other side,
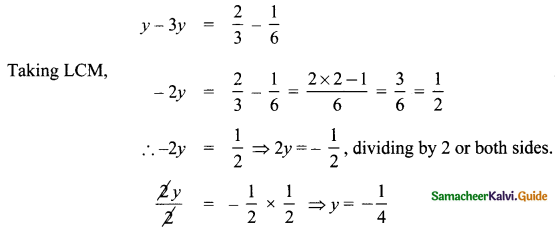
![]()
(iii) \(\frac{1}{3}-\frac{x}{3}=\frac{7 x}{12}+\frac{5}{4}\)
Answer:
Transposing \(\frac{-x}{3}\) to the other side, it becomes + \(\frac{x}{3}\)
∴ \(\frac{1}{3}=\frac{7 x}{12}+\frac{5}{4}+\frac{x}{3}\)
Transposing \(\frac{5}{4}\) to the other side, it becomes \(\frac{-5}{4}\)
\(\frac{1}{3}-\frac{5}{4}=\frac{7 x}{12}+\frac{x}{3}\)
Multiply by 12 throughout [we look at the denominators 3, 4, 12, 3 and take the LCM, which is 12]
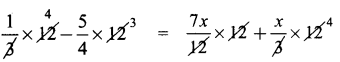
4 – 15 = 7x + x × 4
– 11 = 7x + 4x
11x = – 11
x = -1
Question 5.
Find x
(i) -3(4x + 9) = 21
Answer:
![]()
Expanding the bracket,
-3 × 4 + (-3) × 9 = 21
∴ -12x + (-27) = 21
– 12x – 27 = 21
Transposing – 27 to other side, it becomes +27
– 12 x = 21 + 27 = 48
∴ – 12x = 48 ⇒ 12x = – 48
Dividing by 12 on both sides
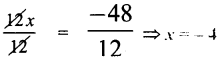
![]()
(ii) 20 – 2 (5 – p) = 8
Answer:
![]()
Expanding the bracket,
20 – 2 × 5 – 2 × (-p) = 8
20 – 10 + 2p = 8
(- 2 × – p = 2p)
10 + 2p = 8 transposing lo to other side
2p = 8 – 10 = – 2
∴ 2p = – 2
∴ p = – 1
(iii) (7x – 5) – 4(2 + 5x) = 10(2 – x)
Answer:
![]()
Expanding the brackets,
7x – 5 – 4 × 2 – 4 × 5x = 10 × 2 + 10 × (-x)
7x – 5 – 8 – 20x = 20 – 10x
7x – 13 – 20x = 20 – 10x
Transposing 10x & – 13, we get
7x – 13 – 20x + 10x = 20
7x – 20x + 10x = 20 + 13, Simplifying,
– 3x = 33
3x = – 33
x = \(\frac{-33}{3}\) = – 11
x = – 11
![]()
Question 6.
Find x and m:
(i) \(\frac{3 x-2}{4}-\frac{(x-3)}{5}=-1\)
Answer:

![]()
(ii) \(\frac{m+9}{3 m+15}=\frac{5}{3}\)
Answer:
Cross multiplying, we get

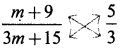
∴ (m + 9) × 3 = 5 × (3m + 15)
m × 3 + 9 × 3 = 5 × 3m + 5 × 15
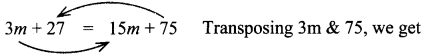
27 – 75 = 15m – 3m
– 48 = 12m

⇒ m = – 4