Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra Ex 3.10 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 3.10
Question 1.
The sum of three numbers is 58. The second number is three times of two-fifth of the first number and the third number is 6 less than the first number. Find the three numbers.
Answer:
Here what we know
a + b + c = 58 (sum of three numbers is 58)
Let the first number be b ‘x’
b = a + 3 (the second number is three times of of the first \(\frac{2}{5}\) number)
b = 3 × \(\frac{2}{5}\)x \(\frac{6}{5}\)x
Third number = x – 6
Sum of the numbers is given as 58.
∴ x + \(\frac{6}{5}\)x + (x – 6) = 58
Multiplying by 5 throughout, we get
5 × x + 6x + 5 × (x – 6) = 58 × 5
5x + 6x + 5x – 30 = 290
∴ 16x = 290 + 30
∴ 16x = 320
∴ x = \(\frac{320}{16}\)
x = 20
1st number = 20
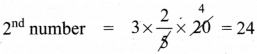
3rd number = 24 – 16 = 14
![]()
Question 2.
In triangle ABC, the measure of ∠B is two-third of the measure of ∠A. The measure of ∠C is 200 more than the measure of ∠A. Find the measures of the three angles.
Answer:
Let angle ∠A be a°
Given that ∠B = \(\frac{2}{3}\) × ∠A = \(\frac{2}{3}\)a
& given ∠C = ∠A + 20 = a + 20
Since A, B & C are angles of a triangle, they add up to 180° (∆ property)
∴∠A + ∠B + ∠C = 180°
⇒a + \(\frac{2}{3}\)a + a + 20 = 180°
\(\frac{3 a+2 a+3 a}{3}\) + 20 = 180°
\(\frac{8 a}{3}\) = 180 – 20 = 160
∴ a = \(\frac{160 \times 3}{8}\) = 60°
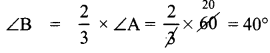
∠C = 80°
![]()
Question 3.
Two equal sides of an isosceles triangle are 5y – 2 and 4y + 9 units. The third side is 2y + 5 units. Find ‘y’ and the perimeter of the triangle.
Answer:
Given that 5y – 2 & 4y + 9 are the equal sides of an isosceles triangle.
∴ The 2 sides are equal
![]()
∴5y – 4y = 9 + 2 (by transposing)
∴ y = 11
∴ 1st side = 5y – 2 = 5 × 11 – 2 = 55 – 2 = 53
2ndside = 53 .
3rdside = 2y + 5 = 2 × 11 + 5 = 22 + 5 = 27
Perimeter is the sum of all 3 sides
∴ P = 53 + 53 + 27 = 133 units
![]()
Question 4.
In the given figure, angle XOZ and angle ZOY form a linear pair. Find the value of x.
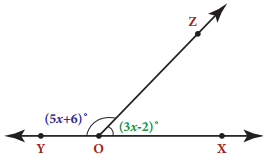
Answer:
Since ∠XOZ & ∠ZOY form a linear pair, by property, we have their sum to be 180°
∴ ∠XOZ + ∠ZOY 180°
∴ 3x – 2 + 5x + 6 = 180°
8x + 4 = 180 = 8x = 180 – 4
∴ 8x = 76 ⇒ x = \(\frac{176}{8}\) ⇒ x = 22°
XOZ = 3x – 2 = 3 × 22 – 2 = 66 – 2 = 64°
YOZ = 5x + 6 = 5 × 22 + 6
= 110 + 6 = 116
![]()
Question 5.
Draw a graph for the following data:

Answer:
Graph between side of square & area
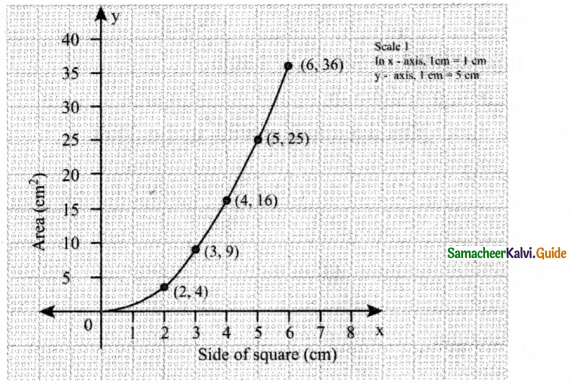
When we plot the graph, we observe that it is not a linear relation.
![]()
Challenging problems
Question 6.
Three consecutive integers, when taken in increasing order and multiplied by 2, 3 and 4 respectIvely, total up to 74. Find the three numbers.
Answer:
Let the 3 consecutive integers be ‘x’, ‘x + 1’ & ‘x + 2’
Given that when multiplied by 2, 3 & 4 respectively & added up, we get 74
![]()
Simplifying the equation, we get
2x + 3x + 3 + 4x + 8 = 74
9x + 11 = 63
9x = 63 ⇒ x = \(\frac{63}{9}\) = 7
First number = 7
Second numbers = x + 1 ⇒ 7 + 1 = 8
Third numbers = x + 2 ⇒ 7 + 2 = 9
∴ The numbers are 7, 8 & 9
![]()
Question 7.
331 students went on a field trip. Six buses were filled to capacity and 7 students had to travel in a van. How many students were there in each bus?
Answer:
Let the number of students in each bus be ‘x’
∴ number of students in 6 buses = 6 × x = 6x
A part from 6 buses, 7 students went in van
A total number of students is 331
∴ 6x + 7 = 331
∴ 6x = 331 – 7 = 324
∴ x = \(\frac{324}{6}\) = 54
∴ There are 54 students in each bus.
![]()
Question 8.
A mobile vendor has 22 items, some which are pencils and others are ball pens. On a particular day, he is able to sell the pencils and ball pens. Pencils are sold for ₹ 15 each and ball pens are sold at ₹ 20 each. If the total sale amount with the vendor is ₹ 380,
how many pencils did he sell?
Answer:
Let vendor have ‘p’ number of pencils & ‘b’ number of ball pens
Given that total number of items is 22
∴ p + b = 22
Pencils are sold for ₹ 15 each & ball pens for ₹ 20 each
total sale amount = 15 × p + 20 × b
= 15p + 20b which is given to be 380.
∴ 15p + 20b = 380
Dividing by 5 throughout,
\(\frac{15 p}{5}+\frac{20 b}{5}\) = \(\frac{380}{5}\) ⇒ – 3p + 4b = 76
Multiplying equation (1) by 3 we get
3 × p + 3 × b = 22 × 3
⇒ 3p + 3b = 66
Equation (2) – (3) gives
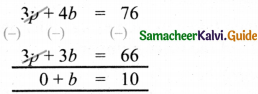
∴ b = 10
∴ p = 12
He sold 12 pencils
![]()
Question 9.
Draw the graph of the lines y = x, y = 2x, y = 3x and y = 5x on the same graph sheet. Is there anything special that you find in these graphs?
Answer:
(i) y = x
(ii) y = 2x,
(iii) y = 3x
(iv) y = 5x
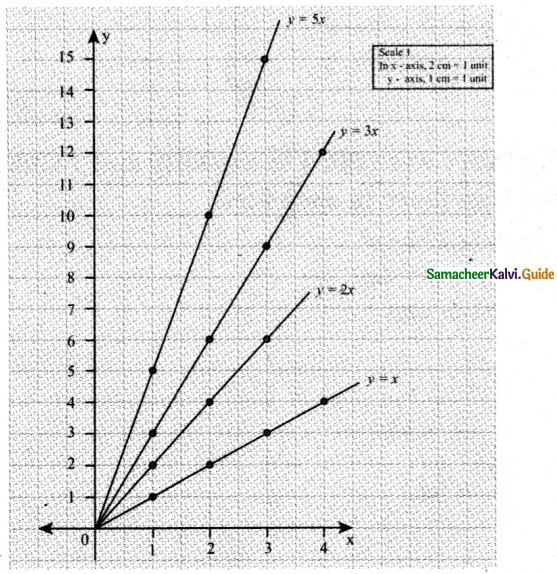
(i) y = x
When x = 1, y = 1
x = 2, y = 2
x = 3, y = 2
(ii) y = 2x
When x = 1, y = 2
x = 2, y = 4
x = 3, y = 6
(iii) y = 3x
When x = 1, y = 3
x = 2, y = 6
x = 3, y = 9
(i) y = 5x
When x = 1, y = 5
x = 2, y = 10
x = 3, y = 15
When we plot the above points & join the points to form line, we notice that the lines become progressively steeper. In other words, the slope keeps increasing.
![]()
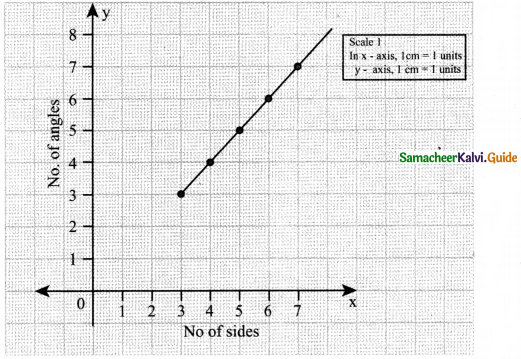
Question 10.
Consider the number of angles of a convex polygon and the number of sides of that polygon. Tabulate as follows:

Use this to draw a graph illustrating the relationship between the number of angles and the number of sides of a polygon.
Answer:
Angles

| Name of Polygon | No of angles | No. of Sides |
| Triangle | 3 | 3 |
| Rectangle | 4 | 4 |
| Pentagon | 5 | 5 |
| Hexagon | 6 | 6 |
| Deptagon | 7 | 7 |
| Octagon | 8 | 8 |
![]()