Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Physics Guide Pdf Chapter 7 Dual Nature of Radiation and Matter Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Physics Solutions
Chapter 7 Dual Nature of Radiation and Matter
12th Physics Guide Dual Nature of Radiation and Matter Text Book Back Questions and Answers
Part – 1:
Text Book Evaluation:
I. Multiple Choice Questions:
Question 1.
The Wavelength λe of an electron and λp of a photon of same energy E are related
by
a) λp α λe
b) λp α \(\sqrt{\lambda_{e}}\)
c) λp α \(\frac{1}{\sqrt{\lambda_{e}}}\)
d) λp α λe2
Answer:
d) λp α λe2
Solution:
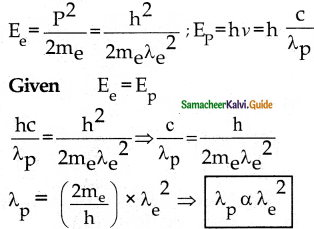
Question 2.
In an electron microscope, the electrons are accelerated by a voltage of 14 kV. If the voltage is changed to 224 kV, then the de Brogue wavelength associated with the electrons would
a) increase by 2 times
b) decrease by 2 times
c) decrease by 4 times
d) increase by 4 times
Answer:
c) decrease by 4 times
Solution:
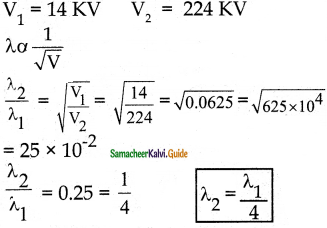
Question 3.
A particle of mass 3 × 10-6 g has the same wavelength as an electron moving with a velocity 6 × 106 m s-1. The velocity of the particle is
a) 1.82 × 10-18 ms-1
b) 9 × 10-2 ms-1
c) 3 × 10-31 ms-1
d) 1.82 × 10-15 ms-1
Answer:
d) 1.82 × 10-15 ms-1
Solution:
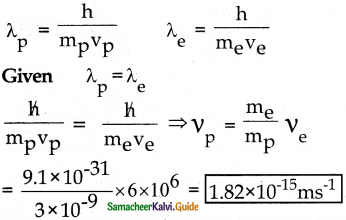
Question 4.
When a metallic surface is illuminated with radiation of wavelength λ, the stopping potential is V. If the same surface is illuminated with radiation of wavelength 2λ, the stopping potential is V/4. The threshold wavelength for the metallic surface is
a) 4λ
b) 5λ
c) \(\frac{5}{2}\)λ
d) 3λ
Answer:
d) 3λ
Solution:
hν – hν0 = eV
\(\frac{\mathrm{hc}}{\lambda}-\frac{\mathrm{hc}}{\lambda_{\mathrm{o}}}\) = eV ………(1)
\(\frac{\mathrm{hc}}{2 \lambda}-\frac{\mathrm{hc}}{\lambda_{\mathrm{a}}}\) = \(\frac{\mathrm{eV}}{4}\) …………(2)
From (1) and (2)
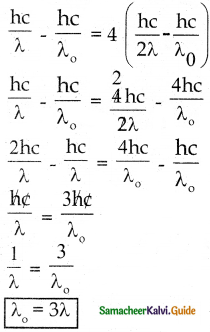
Question 5.
If light of wavelength 330 nm is incident on metal with work function 3.55 eV, the electrons are emitted. Then the wavelength of the emitted electron is (Take h = 6.6 × 10-34 Js)
a) < 2.75 × 10-9 m
b) ≥ 2.75 × 10-9 m
c) ≤ 2.75 × 10-12 m
d) < 2.5 × 10-10 m
Answer:
b) ≥ 2.75 × 10-9 m
Solution:
hv – Φ0 = \(\frac{1}{2}\) mv2 = K.E
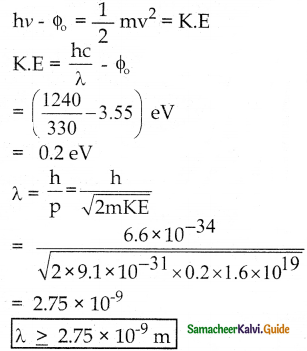
Question 6.
A photoelectric surface is illuminated successively by monochromatic light of wavelength λ and λ/2. If the maximum kinetic energy of the emitted photoelectrons in the second case is 3 times that in the first case, the work function at the surface of material is
a) \(\frac{\mathrm{hc}}{\lambda}\)
b) \(\frac{2 h c}{\lambda}\)
c) \(\frac{\mathrm{hc}}{3 \lambda}\)
d) \(\frac{\mathrm{hc}}{2 \lambda}\)
Answer:
d) \(\frac{\mathrm{hc}}{2 \lambda}\)
Solution:

Question 7.
In photoelectric emission, radiation whose frequency is 4 times the threshold frequency of a certain metal is incident on the metal. Then the maximum possible velocity of the emitted electron will be
a) \(\sqrt{\frac{\mathrm{hv}_{0}}{\mathrm{~m}}}\)
b) \(\sqrt{\frac{6 h v_{0}}{m}}\)
c) \(2 \sqrt{\frac{\mathrm{hv}_{0}}{\mathrm{~m}}}\)
d) \(\sqrt{\frac{\mathrm{hv}_{0}}{2 \mathrm{~m}}}\)
Answer:
b) \(\sqrt{\frac{6 h v_{0}}{m}}\)
Solution:
ν = 4ν0
ν = ?
hν – hν0 = \(\frac{1}{2}\) mv2
4hν0 – hν0 = \(\frac{1}{2}\) mv2
3hν0 = \(\frac{1}{2}\) mv2
ν2 = \(\frac{6 \mathrm{~h} v_{\mathrm{o}}}{\mathrm{m}}\)
⇒ ν = \(\sqrt{\frac{6 h v_{0}}{m}}\)
Question 8.
Two radiations with photon energies 0.9 eV and 3.3 eV respectively are falling on a metallic surface successively. If the work function of the metal is 0.6 eV, then the ratio of maximum speeds of emitted electrons will be
a) 1 : 4
b) 1 : 3
c) 1 : 1
d) 1 : 9
Answer:
b) 1 : 3
Solution:
\(\frac{1}{2}\) mv2 = \(\frac{\mathrm{hc}}{\lambda}\)
\(\frac{1}{2}\) mv12 = 0.9 – 0.6 = 0.3 ……………….(1)
\(\frac{1}{2}\) mv22 = 3.3 – 0.6 = 2.7 ……………….(2)
eqn (1) / (2)
\(\frac{v_{1}^{2}}{v_{2}^{2}}\) = \(\frac{0.3}{2.7}=\frac{1}{9}\)
\(\frac{v_{1}}{v_{2}}=\sqrt{\frac{1}{9}}=\frac{1}{3}\)
ν1 : ν2 = 1 : 3
Question 9.
A light source of wavelength 520 nm emits 1.04 × 1015 photons per second while the second source of 460 nm produces 1.38 × 1015 photons per second. Then the ratio of power of second source to that of first source is
a) 1.00
b) 1.02
c) 1.5
d) 0.98
Answer:
c) 1.5
Solution:

Question 10.
The mean wavelength of light from the sun is taken to be 550 nm and its mean power is 3.8 × 1026 W. The number of photons received by the human eye per second on average from sunlight is of the order of
a) 1045
b) 1042
c) 1054
d) 1051
Answer:
a) 1045
Solution:
Power P = En = \(\frac{\mathrm{hc}}{\lambda}\).n
n = \(\frac{P \lambda}{h c}\)
= \(\frac{3.8 \times 10^{26} \times 550 \times 10^{-9}}{6.6 \times 10^{-34} \times 3 \times 10^{8}}\)
= 105.5 × 1043
n = 1.055 × 1045
Question 11.
The threshold wavelength for a metal surface whose photoelectric work function is 3.313 eV is
a) 4125 Å
b) 3750 Å
c) 6000 Å
d) 2062.5 Å
Answer:
b) 3750 Å
Solution:
Φ = hν0 = \(\frac{\mathrm{hc}}{\lambda_{\mathrm{o}}}\)
λ0 = \(\frac{\mathrm{hc}}{\phi}\)
= \(\frac{6.64 \times 10^{-34} \times 3 \times 10^{8}}{500 \times 10^{-9}}\)
λ0 = 3.757 × 10-7
λ0 = 3750 Å
Question 12.
Light of wavelength 500 nm is incident on a sensitive plate of photoelectric work function 1.235 eV. The kinetic energy of the photoelectrons emitted is (Take h = 6.6 × 10-34 Js)
a) 0.58 eV
b) 2.48 eV
c) 1.24 eV
d) 1.16 eV
Answer:
c)1.24 eV
Solution:
λ = 500 nm;
φ = 1.235 eV
hν = \(\frac{\mathrm{hc}}{\lambda}\)
hν = \(\frac{6.64 \times 10^{-34} \times 3 \times 10^{8}}{500 \times 10^{-9}}\)
= 0.0396 × 10-17
hν = 3.96 × 10-19 J
hν = \(\frac{3.96 \times 10^{-19}}{1.6 \times 10^{-19}}\) = 2.475 evacuated
K.E = hν – φ
= 2.475 – 1.235
= 1.24 eV
Question 13.
Photons of wavelength λ are incident on a metal. The most energetic electrons ejected from the metal are bent into a circular arc of radius R by a perpendicular magnetic field having magnitude B. The work function of the metal is
a) \(\frac{\mathrm{hc}}{\lambda}-\mathrm{m}_{\mathrm{e}}+\frac{\mathrm{e}^{2} \mathrm{~B}^{2} \mathrm{R}^{2}}{2 \mathrm{~m}_{\mathrm{e}}}\)
b) \(\frac{\mathrm{hc}}{\lambda}+2 \mathrm{me}\left[\frac{\mathrm{eBR}}{2 \mathrm{~m}_{\mathrm{e}}}\right]^{2}\)
c) \(\frac{\mathrm{hc}}{\lambda}-\mathrm{m}_{\mathrm{e}} \mathrm{C}^{2} \frac{\mathrm{e}^{2} \mathrm{~B}^{2} \mathrm{R}^{2}}{2 \mathrm{~m}_{\mathrm{e}}}\)
d) \(\frac{\mathrm{hc}}{\lambda}-2 \mathrm{~m}_{\mathrm{e}}\left[\frac{\mathrm{eBR}}{2 \mathrm{~m}_{\mathrm{e}}}\right]^{2}\)
Answer:
d) \(\frac{\mathrm{hc}}{\lambda}-2 \mathrm{~m}_{\mathrm{e}}\left[\frac{\mathrm{eBR}}{2 \mathrm{~m}_{\mathrm{e}}}\right]^{2}\)
Solution:
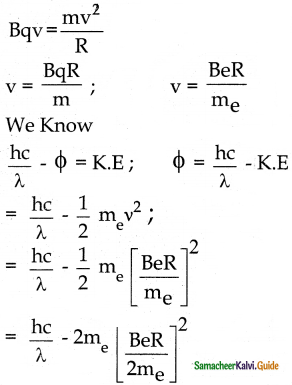
Question 14.
The work functions for metals A, B and C are 1.92 eV, 2.0 eV and 5.0 eV respectively. The metals which will emit photoelectrons for radiation of wavelength 4100 Å is/are
a) A Only
b) both A and B
c) all these metals
d) none
Answer:
b) both A and B
Solution:
Energy in eV = \(\frac{12375}{\lambda}\)
\(\frac{12375}{4100}\) =3.01 eV
Work functions at A and B are less than 3.01 eV so both A and B emit.
Question 15.
Emission of electrons by the absorption of heat energy is called ________ emission
a) photoelectric
b) field
c) thermionic
d) secondary
Answer:
c) thermionic
II. Short Answer Questions:
Question 1.
Why do metals have a large number of free electrons?
Answer:
In metals, the electrons in the outermost shells are loosely bound to the nucleus. Even at room temperature, there are a large number of free electrons which are moving inside the metal in a random manner.
Question 2.
Define the work function of a metal. Give its unit.
Answer:
- The minimum energy needed for an electron to escape from the metal surface is called the work function of a metal.
- It is denoted by Φ0 and its unit is eV
Question 3.
What is the photoelectric effect?
Answer:
The ejection of electrons from a metal plate when illuminated by light or any other electromagnetic radiation of suitable wavelength (or) frequency.
Question 4.
How does photocurrent vary with the intensity of the incident light?
Answer:
Photocurrent – the number of electrons emitted per second is directly proportional to the intensity of the incident light.
Question 5.
Give the definition of intensity of light and its unit.
Answer:
- The intensity is the power of light commonly referred to brightness.
- Its unit is candela (cd).
Question 6.
How will you define threshold frequency?
Answer:
For a given metallic surface, the emission of photoelectrons takes place only if the frequency of the incident light is greater than a certain minimum frequency called the threshold frequency.
Question 7.
What is a photocell? Mention the different types of photocells.
Answer:
photocells: Photoelectric cell or photocell is a device which converts light energy into electrical energy. It works on the principle of the photoelectric effect.
Types:
- Photo emissive cell
- Photovoltaic cell
- Photoconductive cell
Question 8.
Write the expression for the de Broglie wavelength associated with a charged particle of charge q and mass m, when it is accelerated through a potential V
Answer:
- De Broglie wavelength λ = \(\frac{\mathrm{h}}{\sqrt{2 \mathrm{qmv}}}\)
- Where q = ne, h= Planck’s constant
Question 9.
State de Broglie hypothesis.
Answer:
De Broglie’s hypothesis, all matter particles like electrons, protons, neutrons in motion are associated with waves.
Question 10.
Why we do not see the wave properties of a baseball?
Answer:
Since the momentum of a baseball is very low and the wavelength is of the order of 10-34 m the wave properties cannot be seen in a baseball.
Question 11.
A proton and an electron have the same kinetic energy. Which one has a greater de Brogue wavelength? Justify.
Answer:
de-Broglie wavelength of the particle is λ = \(\frac { h }{ p }\) = \(\frac { h }{ \sqrt { 2mK } } \)
i.e. λ ∝ \(\frac { h }{ \sqrt { m } } \)
As me << mp, so λe >> λp
Hence protons have greater de-Broglie wavelength.
Question 12.
Write the relationship of de Broglie wavelength \ associated with a particle of mass m in terms of its kinetic energy K.
1. De Broglie wavelength h h
λ = \(\frac{\mathrm{h}}{\mathrm{m} \cdot \mathrm{v}}\)
= \(\frac{\mathrm{h}}{\sqrt{2 \mathrm{emV}}}\)
2. Since kinetic energy of the electron K = eV then the de Broglie wavelength is given by
λ = \(\frac{\mathrm{h}}{\sqrt{2 \mathrm{mK}}}\)
Question 13.
Name an experiment which shows wave nature of the electron. Which phenomenon was observed in this experiment using an electron beam?
Answer:
- Davisson – Germer experiment confirmed the wave nature of electrons.
- They demonstrated that electron beams are diffracted when they fall on crystalline solids.
Question 14.
An electron and an alpha particle have same kinetic energy. How are the de Broglie wavelengths associated with them related?
Answer:
1. De Broglie wavelength is given by
λ = \(\frac{\mathrm{h}}{\sqrt{2 \mathrm{mK}}}\)
2. Since mα > me
λ α \(\frac{1}{\sqrt{\mathrm{m}}}\) then
λα < λe
3. An α particle having a greater mass than electron so it is having lesser de Broglie wavelength.
III. Long Answer Questions:
Question 1.
What do you mean by electron emission? Explain briefly various methods of electron emission.
Answer:
The liberation of electrons from any surface of a metallic substance is called electron emission.
There are mainly four types of electron emission.
i) Thermionic emission:
1. When a metal is heated to a high temperature, the free electrons on the surface of the metal get sufficient thermal energy so that they are emitted from the metallic surface.
2. The intensity of the thermionic emission depends on the metal used and its temperature.
(Examples: Cathode ray tubes, electrons microscopes, X-ray tubes, etc.)
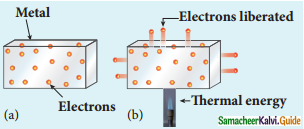
Electrons in the (a) metal (b) heated metal
ii) Field emission:
1. Electron field emission occurs when a very strong electric field is applied across the metal.
2. This strong field pulls the free electrons and helps them to overcome the surface barrier of the metal.
Examples:
Field emission scanning electron microscopes, Field emission display, etc….
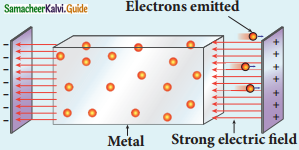
Field emission
iii) Photoelectric emission :
1. When electromagnetic radiation of suitable frequency is incident on the surface of the metal, the energy is transferred from the radiation to the free electrons.
2. Hence the free electrons get sufficient energy to cross the surface barrier and the photoelectric emission takes place.
3. The number of electrons emitted depends on the intensity of the incident radiation.
Examples: Photodiodes, Photoelectric cells, etc.
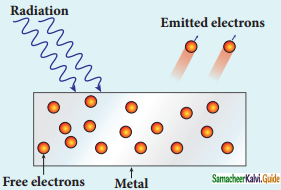
Photoelectric emission
iv) Secondary emission:
1. When a beam of fast-moving electrons strikes the metal surface, the kinetic energy of the striking electrons is transferred to the free electrons on the metal surface.
2. Thus the free electrons get sufficient kinetic energy so that the secondary emission occurs.
Example: Image intensifiers, Photomultiplier tubes, etc..
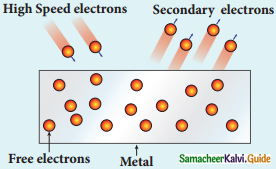
Secondary emission of electrons
Question 2.
Briefly discuss the observations of Hertz, Hallwachs, and Lenard.
Answer:
Hertz Observation:
1. In 1887, Hertz generated and detected electromagnetic waves with his high voltage induction coil to cause a spark discharge between two metallic spheres.
2. When a spark is formed, the charges will oscillate back and forth rapidly and the electromagnetic waves are
produced.
3. The electromagnetic waves thus produced were detected by a detector that has a copper wire bent in the shape of a circle
4. But the tiny spark produced in the detecter cannot be explained by hertz.
Hallwach Observation:
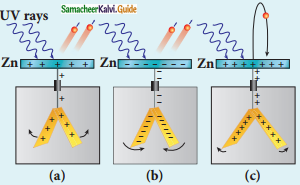
Irradiation of ultraviolet light on
- uncharged zinc plate
- negatively charged plate
- positively charged plate
- In 1888, Hallwach confirmed that the strange behaviour of the spark is due to the action of ultraviolet light.
- A clean circular plate of zinc is mounted on an insulating stand and is attached to a gold leaf electroscope by a wire.
- When the uncharged zinc plate is irradiated by ultraviolet light from an arc lamp, it becomes positively charged and the leaves will open.
- If the negatively charged zinc plate is exposed to ultraviolet light, the leaves will close as the charges leaked away quickly.
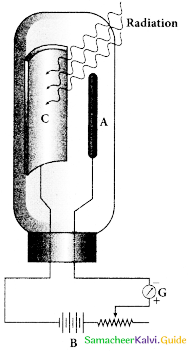
Lenard’s observation:
- In 1902, Lenard constructed an apparatus consists of two metallic plates A and C placed in an evacuated quartz bulb.
- The Galvanometer G and battery B are connected in the circuit.
- When ultraviolet light is incident there is a deflection in the galvanometer.
- If anode A is exposed to ultraviolet light, no current is observed.
- The electron emission observed when ultraviolet light falling on the negative plate called photoelectric emission.
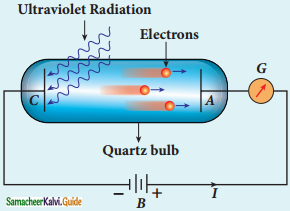
Experimental setup for the study of the photoelectric effect
Question 3.
Explain the effect of potential difference on photoelectric current.
Answer:
1. The effect of potential difference on photoelectric current can be studied by keeping the frequency and the intensity of the incident light constant.
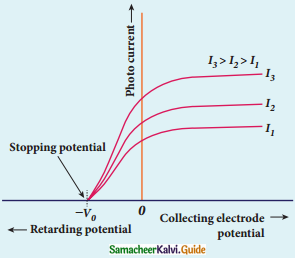
Variation of photocurrent with a potential difference
2. If the cathode is irradiated the potential of A is increased thereby increase in the photocurrent.
3. When all the photoelectrons from C are collected by A the photocurrent reaches a maximum called saturation current.
4. When a negative (retarding) potential is applied to A with respect to C the photoelectrons start to decrease because more and more photoelectrons are being repelled away.
5. The photocurrent becomes zero at a particular negative potential V0 called stopping or cut off potential.
6. The negative potential applied to anode A which is just sufficient to stop the most energetic photoelectrons to make photocurrent zero is called stopping potential.
7. The kinetic energy of the fastest electron (Kmax) is equal to the work done by the stopping potential to stop it (eV0)
Kmax = \(\frac{1}{2}\) mvmax2 = eV0 …………..(1)
where νmax is the maximum speed of the photo electrons
νmax = \(\sqrt{\frac{2 \mathrm{eV}_{\mathrm{o}}}{\mathrm{m}}}\)
= \(\sqrt{\frac{2 \times 1.602 \times 10^{-19}}{9.1 \times 10^{-31}} \times V_{\mathrm{O}}}\)
νmax = 5.93 × 105 \(\sqrt{\mathrm{V}_{\mathrm{O}}}\) …………….(2)
Kmax = eV0 (in Joule) or Kmax = V0 (in eV)
8. The maximum kinetic energy of the photoelectrons is independent of the intensity of the incident light.
Question 4.
Explain how the frequency of incident light varies with stopping potential.
Answer:
1. The effect of frequency of incident light on stopping potential can be studied by keeping the intensity of the incident light constant
2. The electrode potential varies for different frequencies of the incident light.
3. As the frequency is increased the photoelectrons are emitted with greater kinetic energies so that the retarding potential needed to stop the photoelectrons is also greater.
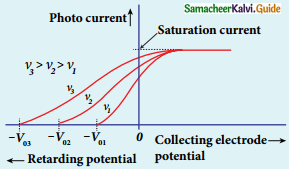
variation or photocurrent with corrector electrode potential for different frequencies of the incident radiation
4. From the graph between frequency and stopping potential, the stopping potential varies linearly with the frequency of the incident light.
5. The stopping potential is zero when no electrons are emitted below a certain frequency called threshold frequency.
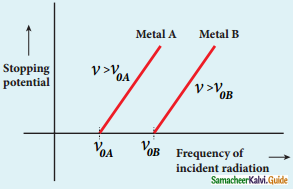
Variation of stopping potential with frequency of the incident radiation for two metals
Question 5.
List out the laws of the photoelectric effect.
Answer:
- For a given frequency of incident light, the number of photoelectrons emitted is directly proportional to the intensity of the incident light.
- The maximum kinetic energy of the photoelectrons is independent of the intensity of the incident light.
- The maximum kinetic energy of the photoelectrons from a given metal is directly proportional to the frequency of incident light.
- For a given surface, the emission of photoelectrons takes place only if the frequency of incident light is greater than a certain minimum frequency called the threshold frequency.
- There is no time lag between the incidence of light and emission of photoelectrons.
Question 6.
Explain Why the photoelectric effect cannot be explained on the basis of the wave nature of light.
Answer:
Failures of classical wave theory:
From Maxwell’s theory, light is an electromagnetic wave consisting of coupled electric and magnetic oscillations that move with the speed of light and exhibit typical wave behaviour. Let us try to explain the experimental observations of the photoelectric effect using wave picture of light.
1. When light is incident on the target, there is a continuous supply of energy to the electrons. According to wave theory, light of greater intensity should impart greater kinetic energy to the liberated electrons (Here, the Intensity of light is the energy delivered per unit area per unit time). But this does not happen. The experiments show that the maximum kinetic energy of the photoelectrons does not depend on the intensity of the incident light.
2. According to wave theory, if a sufficiently intense beam of light is incident on the surface, electrons will be liberated from the surface of the target, however low the frequency of the radiation is. From the experiments, we know that photoelectric emission is not possible below a certain minimum frequency. Therefore, the wave theory fails to explain the existence of threshold frequency.
3. Since the energy of light is spread across the wavefront, the electrons which receive energy from it are large in number. Each electron needs considerable amount of time (a few hours) to get energy sufficient to overcome the work function and to get liberated from the surface. But experiments show that photoelectric emission is almost instantaneous process (the time lag is less than 10“9 s after the surface is illuminated) which could not be explained by wave theory.
Question 7.
Explain the quantum concept of light.
Answer:
Planck’s concepts of quantum :
- Max Planck proposed the quantum concept in 1900 in order to explain the thermal radiations emitted by a black body and the shape of the radiation curves.
- If an oscillator vibrates with frequency ν, its energy can have only certain discrete values.
E = nhν n = 1,2,3………… - Where h is Planck’s constant.
- The oscillators emit or absorb energy in small packets or quanta and the energy of each quantum is E = hν
- Energy is quantized and it is not continuous as believed in the wave nature. This is called the quantization of energy.
Einstein’s concept of quantum:
- Einstein extended Planck’s quantum concept to explain the photoelectric effect in 1905.
- According to Einstein, the energy in light is not spread out over wavefronts but is concentrated in small packets called energy quanta.
- The light of frequency ν from any source having energy E = hν
- The light quanta having the magnitude of linear momentum
p = \(\frac{\mathrm{hv}}{\mathrm{c}}\)
Question 8.
Obtain Einstein’s photoelectric equation with the necessary explanation.
Answer:
When a photon of energy hν is incident on a metal surface, it is completely absorbed by a single electron and the electron is ejected. In this process, a part of the photon energy is used for the ejection of the electrons from the metal surface (photo electric work function Φ0) and the remaining energy is imparted as kinetic energy of the ejected electron.
hν = Φ0 + \(\frac{1}{2}\) mv2 ………………….(1)
Where m is the mass and v is the velocity.
At threshold frequency, ν0
There is no ejection of electrons hence zero kinetic energy then,
hν0 = Φ0 …………………(2)
eqn (1) => hν = hν0 + \(\frac{1}{2}\) mv2 ……………(3)
This is Einsteins photo electric equation.
If the electron does not lose energy by internal collisions, then it is emitted with maximum
kinetic energy Kmax. Then
Kmax = \(\frac{1}{2}\) mvmax2
Where νmax maximum velocity of the electron ejected
Kmax = hν – Φ0 ……………..(4)
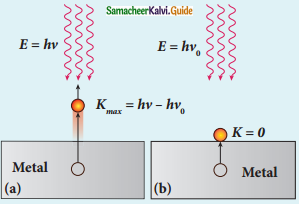
Emission of photoelectrons
A graph between Kmax maximum kinetic energy of a photoelectron and frequency ν of the incident light is a straight line.
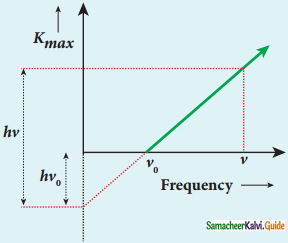
Kmax vs ν graph
Question 9.
Explain experimentally observed facts of the photoelectric effect with the help of Einstein’s explanation.
Answer:
- The experimentally observed facts of the photoelectric effect can be explained with the help of Einstein’s photoelectric equation.
- As each incident photon liberates one electron, then the increase of intensity of the light (the number of per unit area per unit time) increases the number of electrons emitted thereby increasing the photocurrent.
- From Kmax = hν – Φ0 it is evident that Kmax is proportional to the frequency and independent of the intensity of the light.
- From hν = hν0 + \(\frac{1}{2}\) mv2, there must be minimum energy equal to the work function of the metal to liberate electrons from the metal surface. Below which the emission of electrons is not possible.
- There exists a minimum frequency called threshold frequency below which there is no photoelectric emission.
- The transfer of photon energy to the electrons is instantaneous so that no time lag between the incidence of photons and ejection of electrons.
- Thus the photoelectric effect is explained on the basis of the quantum concept of light.
Question 10.
Give the construction and working of a photoemissive cell.
Answer:
Photo emissive cell:
Construction:
Construction of photo cell
1. It consists of an evacuated glass or quartz bulb in which two metallic electrodes, cathode and anode are fixed.
2. The cathode C is Semi cylindrical in shape and is coated with a photo-sensitive material.
3. anode A is a thin rod or wire kept along the axis of the semi-cylindrical cathode.
4. A potential difference is applied between the anode and the cathode through a galvanometer G.
Working:
When cathode is illuminated, electrons are emitted from it. These electrons are attracted by anode and hence a current is produced which is measured by the galvanometer. For a given cathode, the magnitude of the current depends on (i) the intensity of incident radiation and (ii) the potential difference between anode and cathode.
Question 11.
Derive an expression for de Broglie wavelength of electrons.
Answer:
An electron of mass m is accelerated through a potential difference of V volt. The kinetic energy aquired by the electron is given by
\(\frac{1}{2}\) mv2 = eV
Therefore, the speed ν of the electron is
ν = \(\sqrt{\frac{2 \mathrm{eV}}{\mathrm{m}}}\) …………..(1)
From de Broglie equation
λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) = \(\sqrt{\frac{\mathrm{h}}{2 \mathrm{emV}}}\) ……………(2)
Substituting the known values
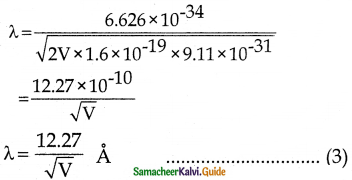
When electron is accelerated with 100 V, then
λ = \(\frac{12.27}{\sqrt{100}}\) = 1.227 Å
Since the kinetic energy of the electron, K = eV, then the de Broglie wavelength associated with electron is given by
λ = \(\frac{\mathrm{h}}{\sqrt{2 \mathrm{mK}}}\) …………..(4)
Question 12.
Briefly explain the principle and working of an electron microscope.
Answer:
Principle:
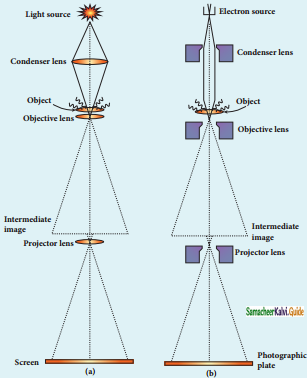
(a) Optical Microscope
(b) Electron Microscope
- The wave nature of the electron is used in the construction of an electron microscope.
- The resolving power of a microscope is inversely proportional to the wavelength of the radiation used.
- Since the de Broglie wavelength of the electron is much smaller than the visible light, the resolving power and the magnification are high.
- Electron microscopes giving magnification more than 2,00,000 times than the optical microscope.
Working:
- The construction and working of an electron microscope are similar to the optical microscope.
- Focussing of electron beam is done by the electrostatic or magnetic lenses.
- The divergence and convergence can be done by adjusting electric and magnetic fields.
- The accelerated electrons from the source with high potential are made parallel by a magnetic condenser lens.
- With the help of a magnetic objective lens and magnetic projector lens system, the magnified image is obtained.
- These electron microscopes are being used in almost all branches of science.
Question 13.
Describe briefly Davisson – Germer experiment which demonstrated the wave nature of electrons.
Answer:
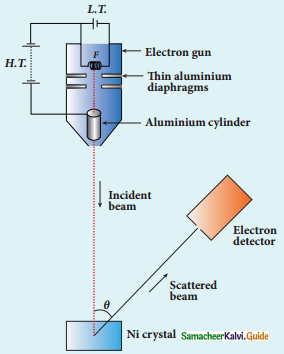
Experimental set up of Davisson – Germer experiment
- De Broglie hypothesis of matter waves was experimentally confirmed by Clinton Davisson and Lester Germer in 1927.
- They demonstrated that electron beams are diffracted when they fall on crystalline solids.
- Since crystals can act as a three-dimensional diffraction grating for matter waves, the electron waves incident on crystals are diffracted off in certain specific directions.
- The filament F is heated by a low tension battery, electrons are emitted from the hot filament by thermionic emission.
- Electrons are accelerated due to-the potential between the filament and the anode aluminium cylinder by a high tension battery.
- The electron beam is collimated and it is allowed to strike a single crystal of nickel by two thin aluminum diaphragms.
- The electron detector measures the intensity of the scattered electron beam.
- The intensity of the scattered beam is measured for various incident angles θ.
- For accelerating voltage of 54 V, the scattered wave shows a peak at an angle of 50° to the incident beam.
- The constructive interference of diffracted electrons for various atomic layers obtained known as interplanar spacing of Nickel.
- The de-Broglie wavelength for V = 54 V is given by,
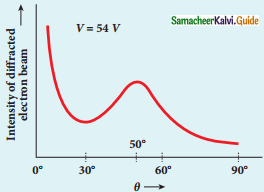
Variation of intensity of diffracted electron beam with the angle
λ = \(\frac{12.27}{\sqrt{\mathrm{V}}}\) Å
λ = \(\frac{12.27}{\sqrt{54}}\)
= 1.67 Å
IV. Numerical Problems:
Question 1.
How many photons per second emanate from a 50 mW laser of 640 nm?
Answer:
Given:
P = 50 × 10-3 W
λ = 640 × 10-9 m
N = ?
N => Number of photons emitted per second.
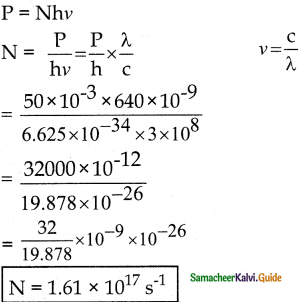
Question 2.
Calculate the maximum kinetic energy and maximum velocity of the photoelectrons emitted when the stopping potential is 81 V for the photoelectric emission experiment.
Answer:
Given:
V = 81 V
EK = ?
EK maximum kinetic energy
vK maximum velocity
\(\frac{1}{2}\) mv2 = eV
EK = 1.6 × 10-19 × 81
= 129.6 × 10-19
EK = 1.3 × 10-17 J
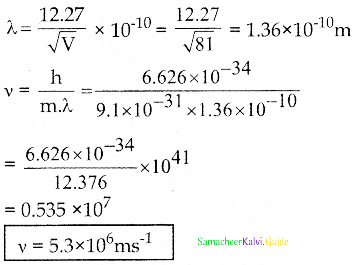
Question 3.
Calculate the energies of the photons associated with the following radiation
(i) violet light of 413 nm,
(ii) X-rays of 0.1 nm,
(iii) radio waves of 10 m
Answer:
E = hν
E = \(\frac{\mathrm{hc}}{\lambda}\) in Joule
E = \(\frac{\mathrm{hc}}{\lambda \mathrm{e}}\) in eV
(i) Violet light of 413 nm
E = \(\frac{6.625 \times 10^{-34} \times 3 \times 10^{8}}{413 \times 10^{-9} \times 1.6 \times 10^{-19}}\)
= \(\frac{19.875}{660.8}\) × 10-26 × 1028
= 0.032 × 102
E = 3 eV
(ii) X-rays of 0.1 nm
= \(\frac{6.625 \times 10^{-34} \times 3 \times 10^{8}}{0.1 \times 10^{-9} \times 1.6 \times 10^{-19}}\)
= \(\frac{19.875 \times 10^{-26}}{0.16 \times 10^{-28}}\)
= 124.24 × 102
E = 12424 eV
(iii) radio waves of 10 m
E = \(\frac{6.625 \times 10^{-34} \times 3 \times 10^{8}}{10 \times 1.6 \times 10^{-19}}\)
= \(\frac{19.875}{1.6}\) × 10-26 × 10-1 × 1019
E = 1.24 × 10-7 eV
Question 4.
A 150 W lamp emits light of mean wavelength of 5500 A. If the efficiency is 12%, find out the number of photons emitted by the lamp in one second.
Answer:
P = 150 W
λ = 5500 × 10-10 m
Eff = 12%
N = \(\frac{\mathrm{P} \lambda}{\mathrm{hc}}\)
= \(\frac{150 \times 5500 \times 10^{-10}}{6.626 \times 10^{-34} \times 3 \times 10^{8}}\)
= \(\frac{825 \times 10^{-7}}{19.878 \times 10^{-26}}\)
= 41.5 × 1019
Number of photons emitted is with 12% efficiency = 41.5 × 1019 × \(\frac{12}{100}\)
N = 4.98 × 1019
Question 5.
How many photons of frequency 1014 Hz will make up 19.86 J of energy?
Answer:
E = 19.86 J
ν = 1014 Hz
E = nhν
n = \(\frac{E}{h v}\)
= \(\frac{19.86}{6.626 \times 10^{-34} \times 10^{14}}\)
= 2.997 × 1020
Number of Photons N = 3 × 1020
Question 6.
What should be the velocity of the electron so that its momentum equals that of 4000 Å wavelength photon.
Answer:
Given:
λ = 4000 × 10-10 m
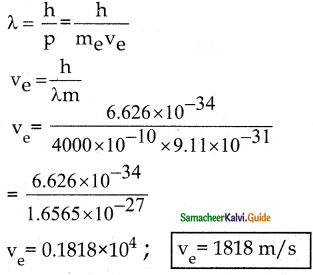
Question 7.
When a light of frequency 9 × 1014 Hz is incident on a metal surface, photoelectrons are emitted with a maximum speed of 8 × 105 ms-1. Determine the threshold frequency of the surface.
Answer:
Given:
ν = 9 × 1014 Hz
ν = 8 × 105ms-1
From Einstein’s photo electric equation
hν = hν0 – \(\frac{1}{2}\) mv2
hν0 = hν – \(\frac{1}{2}\) mv2
ν0 = \(\frac{\mathrm{hv}-1 / 2 \mathrm{mv}^{2}}{\mathrm{~h}}\)
ν0 = ν – \(\frac{\mathrm{mv}^{2}}{2 \mathrm{~h}}\)
= 9 × 1014 – \(\frac{9.1 \times 10^{-31} \times 64 \times 10^{10}}{2 \times 6.626 \times 10^{-34}}\)
= 9 × 1014 – \(\frac{582.4 \times 10^{-21}}{13.252 \times 10^{-34}}\)
= 9 × 1014 – 4.39 × 1014
= (9 – 4.39) × 1014
ν0 = 4.61 × 1014 Hz
Question 8.
When a 6000 A light falls on the cathode of a photocell and produced photoemission. if a stopping potential of 0.8 V is required to stop the emission of an electron, then determine the
(i) frequency of the light
(ii) the energy of the incident photon
(iii) the work function of the cathode material
(iv) threshold frequency and
(v) the net energy of the electron after it leaves the surface.
Answer:
Given:
λ = 6000 × 10-10 m;
eV0 = 0.8 eV
i) ν = \(\frac{C}{\lambda}\)
= \(\frac{3 \times 10^{8}}{6 \times 10^{-7}}\)
= 0.5 × 1015
ν = 5 × 1014 Hz
(ii) E = hν
= \(\frac{6.626 \times 10^{-34} \times 5 \times 10^{14}}{1.6 \times 10^{-19}}\)
= \(\frac{53.13}{1.6}\) × 10-20 × 1019
E = 2.07 eV
(iii) eν0 = \(\frac{1}{2}\) mv2 = 0.8 eV
W = hν – \(\frac{1}{2}\) mv2
= (2.07 – 0.8) eV
W = 1.27 eV
(iv) W = hν0
ν0 = \(\frac{1.27 \times 1.6 \times 10^{-19}}{6.626 \times 10^{-34}}\)
= \(\frac{2.032}{6.626}\) × 1015
ν0 = 3.06 × 1014 Hz
(v) Net Energy = E = hν – hν0
E = (2.07 – 1.27) ev = 0.8 eV
E = 0.8 eV
Question 9.
A 3310 Å photon liberates an electron from a material with energy 3 × 10-19 J while another 5000 Å photon ejects an electron with energy 0.972 × 10-19 J from the same material. Determine the value of Planck’s constant and the threshold wavelength of the material.
Answer:
Given:
λ1 = 3310 × 10-10 m
λ2 = 5000 × 1010 m
K.E1 = 3 × 10-19 J
K.E2 = 0.972 × 10-19 J
i) ν1 = \(\frac{C}{\lambda_{1}}\)
= \(\frac{3 \times 10^{8}}{3310 \times 10^{-10}}\)
= 9.06 × 1014 Hz
ν2 = \(\frac{C}{\lambda_{2}}\)
= \(\frac{3 \times 10^{8}}{5000 \times 10^{-10}}\)
= 6 × 1014 Hz
hν1 = W + K.E1 …………….(1)
hν1 = W + K.E2 …………….(2)
eqn (1) – (2)
h(ν1 – ν2) = K.E1 – K.E2
h(9.06 – 6) × 1014 = 3 × 10-19 – 0.972 × 10-19
h(3.06 × 1014) = 2.028 × 10-19
h = \(\frac{2.028 \times 10^{-19}}{3.06 \times 10^{14}}\)
= 0.662 × 10-33
h = 6.62 × 10-34 Js
ii) 
Question 10.
At the given point of time, the earth receives energy from the sun at 4 cal cm min-1. Determine the number of photons received on the surface of the Earth per cm-2 per minute. (Given: Mean wavelength of sunlight = 5500 Å)
Answer:
Given:
E = 4 cal cm-2 min-1
λ = 5500 × 10-10m
We know that 1 cal = 4.2 J
E = hnν
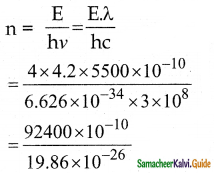
Number of photons n = 4.652 × 1019 per cm2 per minute
Question 11.
UV light of wavelength 1800 Å is incident on a lithium surface whose threshold wavelength 4965 Å. Determine the maximum energy of the electron emitted.
Answer:
Given:
λ = 1800 × 10-10 m
λ0 = 4965 × 10-10 m
hν = hν0 +K.E
h\(\frac{c}{\lambda}\) =h\(\frac{c}{\lambda_{o}}\) + K. E
K.E = \(\frac{\mathrm{hc}}{\lambda}\) – \(\frac{\mathrm{hc}}{\lambda_{\mathrm{o}}}\)
hc = 6.625 × 10-34 × 3 × 108
hc = 19.86 × 10-24
K.E = \(\frac{19.86 \times 10^{-26}}{1800 \times 10^{-10}}\) – \(\frac{19.86 \times 10^{-24}}{4965 \times 10^{-10}}\)
= 0.0110 × 10-16 – 0.004 × 10-16
K.E in eV = \(\frac{7 \times 10^{-19}}{1.6 \times 10^{-19}}\) = 4.375 eV
K.E = 4.4 eV
Question 12.
Calculate the de Brogue wavelength of a proton whose kinetic energy is equal to 81.9 x 1O’ J. (Given: mass of proton is 1836 times that of electron).
Answer:
Given:
K.E = 81.9 × 10-15 J
mp = 836 me

Question 13.
A deuteron and an alpha particle are accelerated with the same potential. Which one of the two has
i) greater value of de Broglie wavelength associated with it and
ii) less kinetic energy? Explain.
Answer:
Given:
deutron => e → 1e \(\left({ }_{1} \mathrm{H}^{2}\right)\)
m → 2m
alpha => e → 2e (2He4)
m → 4m
i) 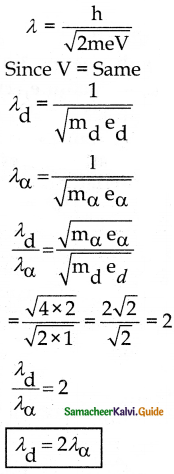
ii) \(\frac{1}{2}\) mv2 = eV
Kd = eV
Kα = 2 eV
Kα = 2 Kd
Kd = \(\frac{\mathrm{K}_{\alpha}}{2}\)
Question 14.
An electron is accelerated thorugh a potential difference of 81 V. What is the de Brogue wavelength associated with it? To which part of electromagnetic spectrum does this wavelength correspond?
Answer:
Given:
V = 81 V
λ = \(\frac{12.27}{\sqrt{\mathrm{V}}}\) Å
λ = \(\frac{12.27}{\sqrt{81}}\) ⇒ λ = \(\frac{12.27}{9}\)
λ = 1.36 Å
Question 15.
The ratio between the de Brogue wavelengths associated with protons. accelerated through a potential of 512 V and that of alpha particles accelerated through a potential of X volts is found to be one. Find the value of X.
Answer:
Given:
For proton charge = e
mass = m
For charge = 2e
mass = 4m
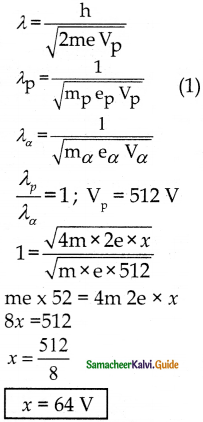
Part II:
12th Physics Guide Dual Nature of Radiation and Matter Additional Questions and Answers
I. Match the following:
Question 1.
| I | II |
| A. Thermionic emission | a. photodiodes |
| B. Field emission | b. cathode-ray tube |
| C. Photoelectric emission | c. Image Identifiers |
| D. Secondary emission | d. Field emission display |
Answer:
A. b
B. d
C. a
D. c
Question 2.
| I | II |
| A. Einstein theory | a. 1902 |
| B. Hertz observation | b. 1905 |
| C. Hallwacks observation | c. 1887 |
| D. Lenard’s observation | d. 1888 |
Answer:
A. b
B. c
C. d
D. a
Question 3.
| I | II |
| A. Photocell | a. metallic cathode |
| B. Photo emissive cell | b. resistance of semi conductors |
| C. Photovoltaic coil | c. light energy into electrical energy |
| D. Photoconductive cell | d. semiconductor voltage |
Answer:
A. c
B. a
C. d
D. b
Question 4.
| I | II |
| A. Hertz | a. production of matter waves |
| B. Einstein | b. wavelength of electrons |
| C. de-Broglie | c. photoelectric equation |
| D. Davisson Germer | d. generated electromagnetic waves |
Answer:
A. d
B. c
C. b
D. a
II. Fill in the blanks:
Question 1.
The liberation of electrons from any surface of a substance is called _______.
Answer:
electron emission
Question 2.
1 eV is equal to ___________ Joule.
Answer:
1.602 × 10-19
Question 3.
The stopping potential is independent of ________ of the incident light.
Answer:
intensity
Question 4.
The quality of X-rays is measured in terms of their _______.
Answer:
penetrating power
Question 5.
The graph between maximum kinetic energy of the photoelectron and frequency of the incident light is ________.
Answer:
straight line
Question 6.
Einstein’s photoelectric equation was experimentally confirmed by ________.
Answer:
Millikan
III. Choose the odd man out:
Question 1.
a) Field emission display
b) Photodiodes
c) Photomultiplier tubes
d) Electron microscope
Answer:
d) Electron MicroScope
Question 2.
a) Work function
b) Discharge tube
c) Threshold frequency
d) Stopping potential
Answer:
b) Discharge tube
Question 3.
a) mass
b) frequency
c) Intensity
d) wavelength
Answer:
a) mass
Question 4.
a) neutrons
b) tungsten
c) particles
d) x-rays
Answer:
a) tungsten
Question 5.
a) Photon
b) electron
c) proton
d) neutron
Answer:
a) photon
IV. Choose the incorrect pair:
Question 1.
| A. Continuous X-rays | All possible wavelength |
| B. Characteristics X-rays | Definite wavelength |
| C. X-ray | Short focal length |
| D. Intensity of X-rays | Constant for all Substances |
Answer:
D) Intensity of X-rays – Constant for all substances
Question 2.
| A. Photo electrons | directly proportional to the intensity of incident radiation |
| B. Kinetic energy of photoelectrons | independent of the intensity of incident light |
| C. Maximum kinetic energy of photoelectrons | directly proportional to the frequency of incident light |
| D. Emission of photoelectrons | does not depend upon the potential of the electrodes |
Answer:
D) Emission of photoelectrons – does not depend upon the potential of the electrodes
Question 3.
| A. Potential barrier | work function |
| B. Stopping potential | Maximum potential between the electrodes |
| C. Threshold frequency | minimum frequency of incident radiation for emission |
| D. Saturation current | Maximum photoelectrons |
Answer:
B) Stopping potential – maximum potential between the electrodes
V. Choose the correct pair:
Question 1.
| A. Continuous X-ray | Λ0 = \(\frac{14200}{\mathrm{~V}}\) Å |
| B. de – Broglie wavelength | 1.67 Å |
| C. Mass of an electron | 9.11 x 10-31 kg |
| D. Charge of an electron | 1.6 x 1019 C |
Answer:
B) de – Broglie wavelength – 1.67 Å
Question 2.
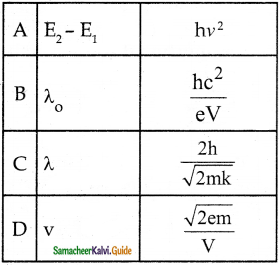
Answer:
D) V = \(\frac{\sqrt{2 \mathrm{em}}}{\mathrm{V}}\)
VI. Assertion and Reason:
Question 1.
Assertion:
The resolving power of the electron microscope is high.
Reason:
The wavelength of electrons is very much lesser than the visible light.
i) Assertion is true but reason is false
ii) The assertion and reason both are false
iii) Both assertion and reason are true and the reason is the correct explanation of the assertion.
iv) Both assertion and reason are true and the reason is not the correct explanation of the assertion.
Answer:
(iii) Both assertion and reason are true and the reason is the correct explanation of the assertion.
Question 2.
Assertion:
The oscillators emit or absorb energy in small packets or quanta.
Reason:
Energy is not discrete, the energy posses wave nature.
i) The assertion and reason both are false
i) The assertion is true but reason is false
iii) The assertion is false but reason is true
iv) Both the assertion and reason are true
Answer:
(ii) The assertion is true but the reason is false
VII. Choose the correct statement:
Question 1.
a) Particle cannot be localised in space and time
b) Wave can be localised in space and time
c) Black body radiation can be explained by wave nature.
d) The minimum energy needed for an electron to escape from the metal surface is called the work function.
Answer:
d) The minimum energy needed for an electron to escape from the metal surface is called the work function.
Question 2.
a) When the momentum of the particle increases de-Broglie wavelength also increases.
b) A photon of energy 2E is an incident on a photosensitive surface of photoelectric work function E. The maximum kinetic energy of photoelectron emitted is 2E.
c) The number of de-Broglie waves of an electron in the nth orbit of an atom is n.
d) The resolving power of the electron microscope is 100 times greater than an optical microscope.
Answer:
b) A photon of energy 2E is an incident on a photosensitive surface of photoelectric work function E. The maximum kinetic energy of the photoelectron emitted is 2E.
VIII. Choose the incorrect statement:
Question 1.
a) Wave mechanical concept of the atom was based on the de-Broglie hypothesis
b) Maximum kinetic energy of the photoelectrons varies linearly with the frequency of incident radiation.
c) The stopping potential of a metal surface is independent of the intensity of the incident radiation.
d) The graph drawn by taking the frequency of the radiation along the x-axis and stopping potential along the y-axis for a photo-sensitive metal is a parabola.
Answer:
d) The graph drawn by taking the frequency of the radiation along the x-axis and stopping potential along the y-axis for a photo-sensitive metal is a parabola.
Question 2.
a) Photoelectric emission is an instantaneous process.
b) Maximum kinetic energy of photoelectrons is directly proportional to the frequency of the incident radiation.
c) Maximum kinetic energy of photoelectrons is indirectly proportional to the intensity of the incident radiation.
d) Photoelectron emission is not possible below a minimum frequency of the incident radiation.
Answer:
c) Maximum kinetic energy of photoelectrons is indirectly proportional to the intensity of incident radiation.
IX. Choose the best answer:
Question 1.
The maximum kinetic energy of photoelectrons emitted from a surface when photons of
energy 3 eV fall on it is 4 eV. The stopping potential, in volt, is
(a) 2
(b) 4
(c) 6
(d) 10
Answer:
(b) 4
Hint:
Stopping potential, V0 = \(\frac { { K }_{ max } }{ e } \) = \(\frac { 4eV }{ e }\) = 4v
Question 2.
The threshold frequency is constant with respect to _______.
a) type of the metal
b) Velocity of electrons
c) Voltage applied
d) intensity of the incident light.
Answer:
a) type of the metal
Question 3.
In a photoemissive cell, the anode is made up of _______.
a) copper
b) gold
c) platinum
d) zinc
Answer:
c) platinum
Question 4.
The work function of a substance is 4.0 eV. The longest wavelength of light that can cause photoelectron emission from this substance is approximately
(a) 540 nm
(b) 400 nm
(c) 310 nm
(d) 220 nm
Answer:
(c) 310 nm
Hint:
λ0 = \(\frac { hc }{ W }\) = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{4.0 \times 1.6 \times 10^{-19}}\) = m = 310 x 10-9 m = 310 nm
Question 5.
Duane-Hunt law is ________.
a) λ = \(\frac{12400}{\mathrm{v}}\) m
b) λ = \(\frac{\mathrm{hc}}{\mathrm{V}}\) m
c) λ = \(\frac{\mathrm{hc}}{\sqrt{\mathrm{E}_{\mathrm{k}}}}\) m
d) none of the above
Answer:
a) λ = \(\frac{12400}{\mathrm{v}}\) m
Question 6.
The resolving power of the electron microscope is _____ times greater than the resolving power of the optical
microscope
a) 102
b) 104
c) 105
d) 103
Answer:
c) c) 105
Question 7.
4 eV is the energy of the incident photon and the work function is 2 eV. The stopping potential will be
(a) 2V
(b) 4V
(c) 6V
(d) 2√2V
Answer:
(d) 2√2V
Hint:
eV0= hv- W0 = 4eV – 2eV = 2eV
∴ V0= \(\frac { 2ev }{ e }\) = 2v
Question 8.
Which of the following graph represents the variation of the particle momentum and associated de Broglie wavelength.
a) 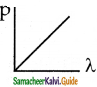
b) 
c) 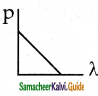
d) 
Answer:
c) 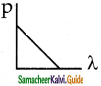
Question 9.
The radiation produced from decelerating electron is called ________.
a) reverse radiation
b) Photon emission
c) black body radiation
d) breaking radiation
Answer:
d) breaking radiation
Question 10.
If the striking electrons knocks of an electron in n = 2 state, the resulting transition give ________.
a) K-lines
b) L-lines
c) M-lines
d) N-lines
Answer:
b) L-lines
Question 11.
When a proton is accelerated through IV, then its kinetic energy will be
(a) 1 eV
(b) 13.6 eV
(c) 1840 eV
(d) 0.54 eV
Answer:
(a) 1 eV
Hint:
K = qV = e x 1V= 1 eV
Question 12.
The work function of a photoelectric material is 3.3 eV. The threshold frequency will be equal to
a) 8 × 1014 Hz
b) 8 × 1010 Hz
c) 5 × 1020 Hz
d) 4 × 1014 Hz
Answer:
a) 8 × 1014 Hz
Solution:
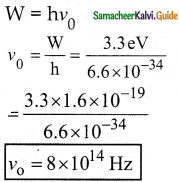
Question 13.
The momentum of the electron having wavelength of 4 Å is
a) 1.6 × 1024 kg ms-1
b) 1.65 × 10-24 kg ms-1
c) 3.3 × 1024 kg ms-1
d) 3.3 × 10-24 kg ms-1
Answer:
b) 1.65 × 10-24 kg ms-1
Solution:
λ = \(\frac{\mathrm{h}}{\mathrm{p}}\)
p = \(\frac{h}{\lambda}\)
= \(\frac{6.6 \times 10^{-34}}{4 \times 10^{-10}}\)
p = 1.65 × 10-24 kgms-1
Question 15.
The number of photo-electrons emitted for the light of a frequency υ (higher than the threshold frequency υ0) is proportional to
(a) Threshold frequency (υ0)
(b) Intensity of light
(c) Frequency of light (υ)
(d) υ – υ0
Answer:
(b) Intensity of light
Hint:
The photoelectric current of Intensity of incident light
Question 15.
The maximum kinetic energy of photoelectrons emitted in a photoelectric effect phenomenon is 3.2eV What is the value of stopping potential to stop the electrons not to reach the anode?
a) 1.6 eV
b) -3.2 eV
c) -1.6 eV
d) -6.4 eV
Answer:
b) -3.2 eV
Solution:
K.Emax = \(\frac{1}{2}\) mv2
V0 = \(\frac{\mathrm{K} . \mathrm{E}}{e}\)
= \(\frac{3.2 \times 1.6 \times 10^{-19}}{1.6 \times 10^{-19}}\)
V0 = -3.2 eV
Question 16.
Radiation of energy 6.2 eV is incident on the metal surface of work function 4.7eV. Find the kinetic energy of the
electrons emitted.
a) 3 × 10-19 J
b) 1.6 × 10-19 J
c) 2.4 × 10-19 J
d) 3.2 × 10-19 J
Answer:
c) 2.4 × 10-19 J
Solution:
hν = 6.2 eV
W = 4.7 eV
\(\frac{1}{2}\) mv2 = hν – W
= (6.2 – 4.7) eV
= 1.5 ev
= 1.5 × 1.6 × 10-19
\(\frac{1}{2}\) mv2 = 2.4 × 10-19 J
K.E = 2.4 × 10-19 J
Question 17.
The de-Broglie wavelength of electrons moving with a speed of 500 km/s
a) 1.45 nm
b) 1.45 Å
c) 1.45 m
d) 4.6 × 1024 HZ
Answer:
a) 1.45 nm
Solution:
λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\)
= \(\frac{6.6 \times 10^{-34}}{9.1 \times 10^{-31} \times 500 \times 10^{3}}\)
λ = 1.45 × 10-19 ;
λ = 1.45 nm
Question 18.
Electron volt is a unit of
(a) Energy
(b) potential
(c) current
(d) charge
Answer:
(a) Energy
Hint:
An electron volt is a unit of energy
Question 19.
The work function of iron is 4.7 V. calculate the cut-off wavelength for this metal.
a) 2633 Å
b) 26.4 × 10-7 m
c) 13.2 × 10-10 m
d) 1320 Å
Answer:
a) 2633 Å
Solution:
hν0 = W;
h\(\frac{\mathrm{C}}{\lambda_{0}}\) = W;
λ0 = \(\frac{\mathrm{hc}}{\mathrm{W}}\)
= \(\frac{6.6 \times 10^{-34} \times 3 \times 10^{8}}{4.7 \times 1.6 \times 10^{-19}}\)
= 2633 × 10-10
λ0 = 2633 Å
Question 20.
The time taken by a photoelectron to come out after photon strikes is approximately
(a) 10-14 s
(b) 10-10 s
(c) 10-16 s
(d) 10-1 s
Answer:
(b) 10-10 s
Hint:
The time lag between the incident of photon and the emission of photoelectrons is 10-10 s approximately.
Question 21.
A Coolidge tube operates at 37200 V maximum frequency of x rays emitted is _______.
a) 9 × 1028 Hz
b) 100 Hz
c) 9 × 1018 Hz
d) 3 × 1018 Hz
Answer:
c) 9 × 1018 Hz
Solution:
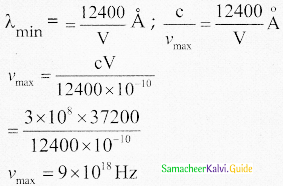
Question 22.
De – Broglie wavelength of an electron accelerating by 100 V
a) 1.227 Å
b) 122.7 μm
c) 0.2227 m
d) 12.27 Å
Answer:
a) 1.227 Å
Solution:
λ = \(\frac{12.27}{\sqrt{\mathrm{V}}}\)
= \(\frac{12.27}{\sqrt{100}}\)
= \(\frac{12.27}{10}\)
λ = 1.227 Å
Question 23.
The energy of photon of wavelength λ is
(a) \(\frac { hc }{ λ }\)
(b) hλc
(c) \(\frac { λ }{ hc }\)
(d) \(\frac { hλ }{ c }\)
Answer:
(a) \(\frac { hc }{ λ }\)
Hint:
E = hυ = \(\frac { hc }{ λ }\)
X. Two Mark Questions:
Question 1.
Why electron is preferred over X-ray in the microscope?
Answer:
- The de-Broglie wavelength of an electron is very less compared to X-rays.
- We can build a high resolving power microscope using electrons.
- Resolving power of a microscope inversely proportional to the wavelength
r0 α \(\frac{1}{\lambda}\)
Question 2.
What are photoelectrons?
Answer:
These are the electrons emitted from a metal surface when it is exposed to electromagnetic radiations of a suitable frequency.
Question 3.
What are matter waves?
Answer:
The moving elementary particles behave as waves under suitable conditions. These waves associated with particles are called matter waves or de-Broglie waves.
Question 4.
What are continuous x rays?
Answer:
Continuous x-ray spectrum consists of radiations of all possible wavelengths from a certain lower limit to higher values continuously as in the case of visible light.
Question 5.
Why is a photo-cell also called an electric eye?
Answer:
Like an eye, a photo-cell can distinguish between weak and intense light. But a photocell gives a measure of light intensity in terms of photoelectric current. So it is also called an electric eye.
Question 6.
What is a photoemissive cell?
Answer:
Its working depends on the electron emission from a metal cathode due to irradiation of light and other radiation.
Question 7.
What are X-ray spectra?
Answer:
X-rays are produced when fast-moving electrons strike the metal target. The intensity of the X-rays when plotted against its wavelength gives a curve called X-ray spectrum.
Question 8.
What are photoconductive cells?
Answer:
The resistance of the semiconductor changes in accordance with the radiation energy incident on it.
Question 9.
Define resolving power of the microscope.
Answer:
The resolving power of a microscope is inversely proportional to the wavelength of the radiation used.
Question 10.
Who invented the particle nature of light?
Answer:
Hertz confirmed that the light is an electromagnetic wave. But the same experiment also produced the first evidence for particle nature of light.
Question 11.
Define intensity of light.
Answer:
Intensity denotes power of light means brightness.
Question 12.
What is diffraction?
Answer:
The bending of light waves round the edges of obstacles is called diffraction.
Question 13.
When light behaves like waves and matter?
Answer:
Light behaves as a wave during its propagation and behaves as a particle during its interaction with matter.
XI. Three Marks Questions:
Question 1.
What is nature of light?
Answer:
The wave nature of light explains phenomena such as interference, diffraction, and polarisation. Certain phenomenon like black body radiation and photoelectric effect light behaves as particles. Thus light posses dual nature, that is particle and wave.
Question 2.
Define one electron volt.
Answer:
One electron volt is defined as the kinetic energy gained by an electron when accelerated by a potential difference of 1 V.
1 eV = K.E gained by the electron or workdone by the electric field
1 eV = qv = 1.602 × 10-19 C × 1 V
1 eV = 1.602 × 10-19 J
Question 3.
Differentiate particle and wave.
Answer:
Particle is a material object which is considered as a tiny concentration of matter localized in space and time whereas wave is a broad distribution of energy not localized in space and time.
XII. Five Mark Questions:
Question 1.
What are the applications of the photocells?
Answer:
- Photocells have many applications especially switches and sensors.
- Automatic switching ON and OFF ordinary lights as well as street lights
- They are used for the reproduction of sound in motion pictures.
- Photocells are used as timers to measure the speeds of athletes during a race.
- Photocells are used to measure the intensity of the given light and to calculate the exact time of exposure.
Question 2.
Write down the characteristics of photons.
Answer:
Characteristics of photons:
According to the particle nature of light, photons are the basic constituents of any radiation and possess the following characteristic properties:
- The photons of light of frequency v and wavelength λ will have energy, given by E = hυ = \(\frac { hc }{ λ }\).
- The energy of a photon is determined by the frequency of the radiation and not by its intensity and the intensity has no relation with the energy of the individual photons in the beam.
- The photons travel with the velocity of light and its momentum is given by p
- Since photons are electrically neutral, they are unaffected by electric and magnetic fields.
- When a photon interacts with matter (photon-electron collision), the total energy, total linear momentum, and angular momentum are conserved. Since photon may be absorbed or a new photon may be produced in such interactions, the number of photons may not be conserved
Question 3.
Write a note on characteristic X-rays. Give the applications of X-rays in medical therapy and industry.
Answer:
Characteristic X-ray Spectra:
1. X-ray spectra snow some narrow peaks at some, well-defined wavelengths when the target is hit by fast electrons. The line spectrum showing these peaks is called the characteristic X-ray spectrum.
2. When an energetic electron removes electrons from K-shell electrons then the electrons from the outer orbit jump to fill the vacancy.
3. Energy difference between the levels is given out as X-ray photon of definite wavelength.
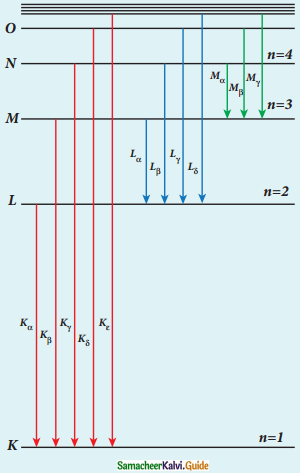
Origin of characteristics X-ray Spectra
K-Series (Kα and Kβ): This line is due to electronic transitions from L, M, and N shells to K-level.
L-Series (Lα and Lβ): It arises due to electronic transitions from M, N, and O shells.
Uses of X-rays:
- Medical diagnosis: used to detect fractures, foreign bodies, diseased organs, etc.
- Medical therapy: To kill diseased tissues, they are employed to cure skin diseases, malignant tumors.
- Industry: To check for flaws in welded joints, motor tires, tennis balls, and wood. At the customs post, they are used for the detection of contraband goods.
- Scientific research: To study crystalline structure i.e. arrangement of atoms and molecules in crystals.
XIII. Conceptual Questions:
Question 1.
Are other particles, other than electrons having a wave nature?
Answer:
The particles like neutrons and alpha particles are also associated with waves. They undergo diffraction when they scattered by suitable crystals.
Question 2.
Why diffraction effects of ordinary light is very small?
Answer:
The wavelength of light is high compared to the spacing between the lattice planes so that the diffraction pattern of ordinary light is less pronounced.
Question 3.
Why crystals are used for three-dimensional grating?
Answer:
The wavelength of X-rays are in the order of 10-10 m which is comparable to the spacing between the crystal lattice planes. Since the crystals can serve as three-dimensional grating.
XIV. Additional Problems:
Question 1.
Calculate the momentum and the de- Broglie wavelength of an electron with kinetic energy 25 eV.
Solution
i) Momentum of the electron:
p = \(\sqrt{2 \mathrm{mk}}\)
= \(\sqrt{2 \times 9.1 \times 10^{-31} \times 25 \times 1.6 \times 10^{-19}}\)
= \(\sqrt{728 \times 10^{-50}}\)
= 26.98 × 10-25 kgms-1
ii) de Broglie wavelength:
λ = \(\frac{\mathrm{h}}{\mathrm{p}}\)
= \(\frac{6.626 \times 10^{-34}}{26.98 \times 10^{-25}}\)
= 0.2455 × 10-34 × 1025
= 0.2455 ×109
λ = 2.455 Å
Question 2.
Monochromatic light of frequency 6 x 1014 Hz is produced by a laser. The power emitted is 2 x 10-3w.
(i) What is the energy of each photon in the light?
(ii) How many photons per second, on average, are emitted by the source?
Solution:
(i) Energy of each photon,
E = hυ = 6.6 x 10-34 x 6 x 1014
E = 3.98 x 10-19J
(ii) If N is the number of photons emitted per second by the source, then
Power transmitted in the beam = N x energy of each photon
P = N
N = \(\frac { P }{ E }\) = \(\frac{2 \times 10^{-3}}{3.98 \times 10^{-19}}\)
N = 5 x 1015 Photons per second.
Question 3.
A proton is moving at a speed of 0.900 times the velocity of light. Find the kinetic energy in Joules and Mev.
Answer:
Given:
ν = 0.9 × 3 × 108 ms-1
Mass of proton m = 1.6 × 10-27 kg
K.E = \(\frac{1}{2}\) mv2
= \(\frac{1}{2}\) × 1.673 × 10-27 × 2.7 × 2.7 × 1016
= \(\frac{6.098 \times 10^{-11}}{1.6 \times 10^{-19}}\)
= 3.811 × 108 eV
K.E = 3.81 MeV
Question 4.
Calculate the momentum of an electron with kinetic energy 2 eV.
Answer:
Given:
K.E = 2 eV
p = \(\sqrt{2 \mathrm{mk}}\)
p = \(\sqrt{2 \times 9.1 \times 10^{-31} \times 2 \times 1.6 \times 10^{-19}}\)
p = 7.63 × 10-25 kgms-1
Question 5.
Calculate the cut-off wavelength and cut off frequency of X-rays from an X-ray tube of accelerating potential 20,000 V.
Answer:
The cut-off wavelength of the characteristic X-rays is
λ0 = \(\frac{12400}{\mathrm{v}}\) Å = \(\frac{12400}{20000}\) Å
= 0.62 Å
The corresponding frequency is
ν0 = \(\frac{c}{\lambda_{0}}\)
= \(\frac{3 \times 10^{8}}{0.62 \times 10^{-10}}\)
= 4.84 × 1018 Hz
Question 6.
What is the (a) momentum, (b) speed, and (c) de-Broglie wavelength of an electron with the kinetic energy of 120 eV.
Solution:
Kinetic energy, K.E = 120 eV = 120 x 1.6 x 10-19
K = K.E = 1.92 x 10-17 J
(a) Momentum of an electron, P = \(\sqrt { 2mK } \)
P = \(\sqrt{2 \times 9.1 \times 10^{-31} \times 1.92 \times 10^{-17}}\)
P = 5.91 x 10-24 kg ms-1
(b) Speed of an electron,
v = \(\frac { p }{ m }\) = \(\frac{5.91 \times 10^{-24}}{9.1 \times 10^{-31}}\) = 6.5 x 106 kg ms-1
(c) de-Broglie wavelength,
λ = \(\frac { h }{ p }\) = \(\frac{6.6 \times 10^{-34}}{5.91 \times 10^{-24}}\) = 1.117 x 10-10 = 0.112 x 10-9 m
λ = 0.112 nm