Samacheer Kalvi 12th Physics Guide Chapter 1 Electrostatics

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Physics Guide Pdf Chapter 1 Electrostatics Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Physics Solutions Chapter 1 Electrostatics

12th Physics Guide Electrostatics Book Back Questions and Answers

Part – I:
I. Multiple choice questions:

Question 1.
Two identical point charges of magnitude – q are fixed as shown in the figure below. A third charge +q is placed midway between the two charges at the point P. Suppose this charge +q is displaced a small distance from the point P in the directions indicated by the arrows, in which direction(s) will +q be stable with respect to the displacement?

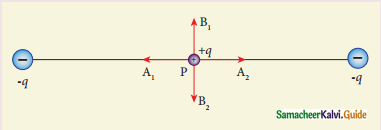
(a) A₁ and A₂
(b) B₁ and B₂
(c) both directions
(d) No stable
Answer:
(b) B₁ and B₂
Solution:
The potential due to an electric dipole along the equatorial line is zero.

Question 2.
Which charge configuration produces a uniform electric field?
(a) point charge
(b) uniformly charged infinite line
(c) uniformly charged infinite plane
(d) uniformly charged spherical shell
Answer:
c) uniformly charged infinite plane
Solution:

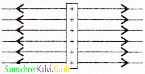
Uniform field lines are represented by equidistant parallel lines.

Question 3.
What is the ratio of the \(\left|\frac{\mathrm{q}_{1}}{\mathrm{q}_{2}}\right|\) charges for the following electric field line pattern?

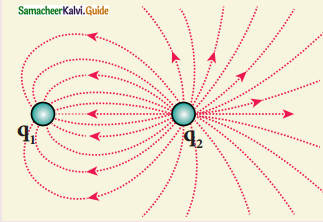
(a) \(\frac{1}{5}\)
(b) \(\frac{25}{11}\)
(c) 5
(d) \(\frac{11}{25}\)
Answer:
(d) \(\frac{11}{25}\)
Solution:
Here q₁ is a negative charge and q₂ is a positive charge
Hint:
Count the number of lines on each charge.

Question 4.
An electric dipole is placed at an alignment angle of 30° with an electric field of 2 × 10⁵ NC^-1. It experiences a torque equal to 8 Nm. The charge on the dipole if the dipole length is lcm is
(a) 4 mC
(b) 8 mC
(c) 5 mC
(d) 7 mC
Answer:
(b) 8 mC
Solution:
T = PE sin θ
T = (q × 21)E sin30°
q = (q × 10^-2) × 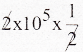q = 8 × 10^-2c

Question 5.
Four Gaussian surfaces are given below with charges inside each Gaussian surface. Rank the electric flux through each Gaussian surface in increasing order:

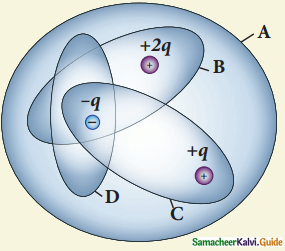
(a) D < C < B < A
(b) A < B = C < D
(c) C < A – B < D
(d) D > C > B > A
Answer:
(a) D < C < B < A
Hint :
flux depends on charge

Question 6.
The total electric flux for the following closed surface which is kept inside water:

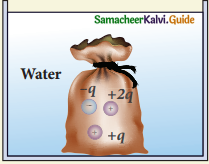
(a) \(\frac{80 \mathrm{q}}{\varepsilon_{\mathrm{o}}}\)
(b) \(\frac{\mathrm{q}}{40 \varepsilon_{0}}\)
(c) \(\frac{\mathrm{q}}{80 \varepsilon_{\mathrm{o}}}\)
(d) \(\frac{\mathrm{q}}{160 \varepsilon_{0}}\)
Answer:
(b) \(\frac{\mathrm{q}}{40 \varepsilon_{0}}\)
Solution:

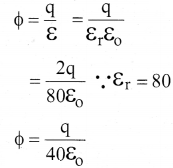
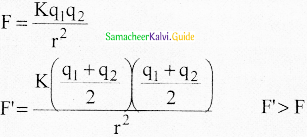
Question 7.
Two identical conducting balls having positive charges q₁ and q₂ are separated by a center to center distance r. If they are made to touch each other and then separated to the same distance, the force between them will be
(a) less than before
(b) same as before
(c) more than before
(d) zero
Answer:
(c) more than before
Solution:

Question 8.
Rank the electrostatic potential energies for the given system of charges in increasing order:

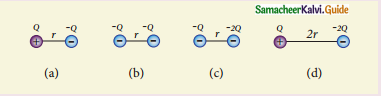
(a) 1 = 4 < 2 < 3
(b) 2 = 4 < 3 < 1
(c) 2 = 3 < 1 < 4
(d) 3 < 1 < 2 < 4
Answer:
(a) 1 = 4 < 2 < 3
Solution:

Question 9.
An electric field \(\overrightarrow{\mathrm{E}}\)= 10 × Î exists in a certain region of space. Then the potential difference V = V_o – V_A, where V_o is the potential at the origin and V_A is the potential at x = 2 m is:
(a) 10 V
(b) -20 V
(c) +20 V
(d) -10 V
Answer:
(c) +20 V
Solution:
E = \(-\frac{d v}{d x}\)
dv = E.dx
= l0x
= 10 × 2
dv = 20 V

Question 10.
A thin conducting spherical shell of radius R has a charge Q which is uniformly distributed on its surface. The correct plot for electrostatic potential due to this spherical shell is
(a)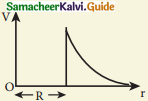

(b)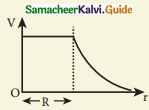

(c)

(d)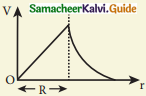
Answer:
(b)
Solution:
In a spherical shell, the electric field inside is zero. But the electric potential is constant.
\(\mathrm{V}=\frac{\mathrm{q}}{4 \pi \varepsilon_{\mathrm{o}} \mathrm{r}}\) as distance increases its potential decrease non-linearly.

Question 11.
Two points A and B are maintained at a potential of 7 V and -4 V respectively. The work done in moving 50 electrons from A to B is
(a) 8.80 × 10^-17 J
(b) -8.80 × 10^-17 J
(c) 4.40 × 10^-17 J
(d) 5.80 × 10^-17 J
Answer:
(a) 8.80 × 10^-17 J
Solution:
W_A→B = (V_A – V_B)q
=(7+4)ne
= 11 × 50 × 1.6 × 10^-19
=8.8 × 10^-17

Question 12.
If the voltage applied on a capacitor is increased from V to 2V, choose the correct conclusion.
(a) Q remains the same, C is doubled
(b) Q is doubled, C doubled
(c) C remains the same, Q doubled
(d) Both Q and C remain the same
Answer:
(c) C remains the same, Q doubled
Solution:

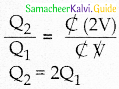
Question 13.
A parallel plate capacitor stores a charge Q at a voltage V. Suppose the area of the parallel plate capacitor and the distance between the plates are each doubled then which is the quantity that will change?
(a) Capacitance
(b) Charge
(c) Voltage
(d) Energy density
Answer:
(d) Energy density

Question 14.
Three capacitors are connected in a triangle as shown in the figure. The equivalent capacitance between points A and C is

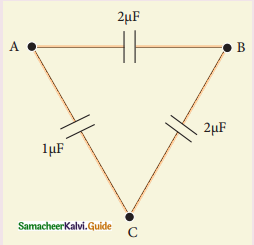
(a) 1 μF
(b) 2 μF
(c) 3 μF
(d) \(\frac{1}{4}\)μF
Answer:
(b) 2 μF
Solution:

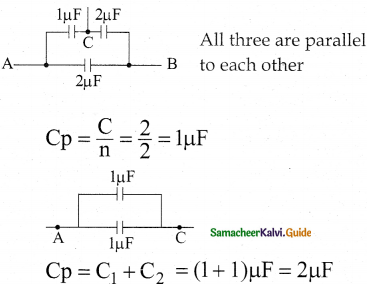
Question 15.
Two metallic spheres of radii 1 cm and 3 cm are given charges of -1 × 10^-2 C and 5 × 10^-2 C respectively. If these are connected by a conducting wire, the final charge on the bigger sphere is
(a) 3 × 10^-2 C
(b) 4 × 10^-2 C
(c) 1 × 10^-2 C
(d) 2 × 10^-2 C
Answer:
(a) 3 × 10^-2 C
Solution:
Total charge Q = q₁ + q₂ = 4 × 10^-2 C
charge on bigger sphere,
q₂ = Q\(\left(\frac{r_{2}}{r_{1}+r_{2}}\right)\)
= 4 × 10^-2 × \(\frac{3}{4}\)
q₂ = 3 × 10^-2 C

II. Short Answer Questions:

Question 1.
What is meant by the quantization of charges?
Answer:
The charge q on any object is equal to an integral multiple of this fundamental unit of charge e.
q = ne
Here n is an integer (0, ±1, ±2, ±3, ±4).
This is called quantisation of electric charge.

Question 2.
Write down Coulomb’s law in vector form and mention what each term represents.
Answer:
The force on the point charge q₂ exerted by another point charge q₁

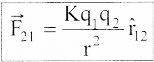
where r̂₂ is the unit vector directed from charge q₁ to charge q₂, and ‘K’ is the proportionality constant K = \(\frac{1}{4 \pi \varepsilon_{0}}\); ε₀ is the permittivity of free space.

Question 3.
What are the differences between the Coulomb force and the gravitational force?
Answer:

• The gravitational force between two masses is always attractive but Coulomb’s force between two charges can be attractive or repulsive, depending on the nature of charges.
• The value of the gravitational constant G = 6.626 x 10^-11 N m² kg^-2. The value of the constant k in Coulomb law is k = 9 x 10⁹ N m² C².
• The gravitational force between two masses is independent of the medium. The electrostatic force between the two charges depends on the nature of the medium in which the two charges are kept at rest.
• The gravitational force between two point masses is the same whether two masses are at rest or in motion. If the charges are in motion, yet another force (Lorentz force) comes into play in addition to Coulomb force.

Question 4.
Write a short note on the superposition principle.
Answer:

1. The superposition principle explains the interaction of multiple charges.
2. The total force acting on a given charge is equal to the vector sum of forces exerted on it by all the other charges.
3. The force on q1 exerted by the charge q<₂ is \(\overrightarrow{\mathrm{F}}_{12}=\mathrm{K} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}_{21}^{2}} \hat{\mathrm{r}}_{21}\)
4. The force on q1 exerted by the charge q<₃ is \(\overrightarrow{\mathrm{F}}_{13}=\mathrm{K} \frac{\mathrm{q}_{1} \mathrm{q}_{3}}{\mathrm{r}_{31}^{2}} \hat{\mathrm{r}}_{31}\)
5. \(\overrightarrow{\mathrm{F}}_{1}^{\text {tot }}=\mathrm{K}\left\{\frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}_{21}^{2}} \hat{\mathrm{r}}_{21}+\frac{\mathrm{q}_{1} \mathrm{q}_{3}}{\mathrm{r}_{31}^{2}} \hat{\mathrm{r}}_{31}+\ldots \frac{\mathrm{q}_{1} \mathrm{q}_{\mathrm{n}}}{\mathrm{r}_{\mathrm{n}}^{2}} \hat{\mathrm{r}}_{\mathrm{n}_{i}}\right\}\)
   

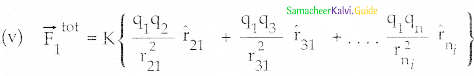
Question 5.
Define ‘electric field’.
Answer:
The electric field at the point P at a distance r from the point charge q is the force experienced by a unit charge and is given by
\(\vec { E } \) = \(\frac { \vec { F } }{ { q }_{ 0 } } \)
The electric field is a vector quantity and its SI unit is Newton per Coulomb (NC^-1).

Question 6.
What is mean by ‘electric field lines?
Answer:
Electric lines of force is an imaginary straight or curved path in which unit positive charge tends to move in the presence of an electric field.

Question 7.
The electric field lines never intersect. Justify.
Answer:
As a consequence, if some charge is placed at the intersection point, then it has to move in two different directions at the same time, which is physically impossible. Hence, electric field lines do not intersect.

Question 8.
Define ‘electric dipole’. Give the expression for the magnitude of its electric dipole moment and the direction.
Answer:

1. Two equal and opposite charges separated by a very small distance constitute an electric dipole.
   Ex:- Carbondioxide, Water.
2. The magnitude of the dipole moment is given by the product of the magnitude of the one of the charges and the distance between them.
   \(|\overrightarrow{\mathrm{P}}|=2 \mathrm{qa}\)
   \(\overrightarrow{\mathrm{P}}=\mathrm{qr}_{+}+(-\mathrm{q}) \overrightarrow{\mathrm{r}}_{-}\)
   where r̂₊ is the position of vector of +1 from the origin and r̂_– is the position vector of -q from the origin
   \(\overrightarrow{\mathrm{P}}=\mathrm{qai}-\mathrm{qa}(-\hat{i})=2 \mathrm{qai}\)
3. It is a vector quantity having direction along the dipole axis -q to +q.
4. Unit: coulomb metre (Cm).

Question 9.
Write the general definition of electro dipole moment for a collection of point charge.
Answer:
The electric dipole moment vector lies along the line joining two charges and is directed from -q to + q. The SI unit of dipole moment is coulomb meter (Cm).
\(\vec { P } \) = qa\(\hat{i} \) -qa(\(\hat{-i} \)) = 2 qa\(\hat{i} \)

Question 10.
Define ‘electrostatic potential’.
Answer:
The electric potential at a point P is equal to the work done by an external force to bring a unit positive charge with constant velocity from infinity to the point P in the region of the external electric field \(\overrightarrow{\mathrm{E}}\).

Question 11.
What is an equipotential surface?
Answer:
An equipotential surface is a surface on which all the points are at the same potential.

Question 12.
What are the properties of an equipotential surface?
Answer:

1. The work done to move a charge ‘q’ between two points lie on equipotential surface is zero.
2. The electric field is normal to an equipotential surface.

Question 13.
Give the relation between electric field and electric potential.
Answer:
Consider a positive charge q kept fixed at the origin. To move a unit positive charge by a small distance dx in the electric field E, the work done is given by dW = -E dx. The minus sign implies that work is done against the electric field. This work done is equal to an electric potential difference. Therefore,
dW = dV.
(or) dV = -Edx
Hence E = \(\frac { dV }{ dx }\)
The electric field is the negative gradient of the electric potential.

Question 14.
Define ‘electrostatic potential energy’.
Answer:
It is defined as the amount of work done in assembling the charges at their locations by bringing them in from infinity.

Question 15.
Define ‘electric flux’.
Answer:
The number of electric field lines crossing a given area kept normal to the electric field lines is called electric flux. Its unit is N m² C^-1. Electric flux is a scalar quantity.

Question 16.
What is meant by electrostatic energy density?
Answer:

1. The energy stored per unit volume of space is defined electrostatic energy density.
   \(\mathrm{U}_{\mathrm{E}}=\frac{\mathrm{U}}{\text { Volume }}=\frac{1}{2} \varepsilon_{\mathrm{o}} \mathrm{E}^{2}\)
2. U – electrostatic potential energy
3. E – electric field
4. £0 – permittivity of free space

Question 17.
Write a short note on ‘electrostatic shielding’.
Answer:
Consider a cavity inside the conductor. Whatever the charges at the surfaces and whatever the electrical disturbances outside, the electric field inside the cavity is zero. A sensitive electrical instrument which is to be protected from external electrical disturbance is kept inside this cavity. This is called electrostatic shielding.

Question 18.
What is Polarisation?
Answer:
Polarisation is defined as the total dipole moment per unit volume of the dielectric.
\(\begin{array}{l}
\vec{p}=\chi_{\mathrm{e}} \overrightarrow{\mathrm{E}}_{\text {ext }} \\
\chi_{\mathrm{e}}=\text { electric susceptibility }
\end{array}\)

Question 19.
What is dielectric strength?
Answer:
The maximum electric field the dielectric can withstand before it breakdowns is called dielectric strength.

Question 20.
Define ‘capacitance’. Give its unit.
Answer:

• It is defined as the ratio of the magnitude of the charge on either of the conductor plates to the potential difference existing between the conductors.
• Unit: farad (or) C/V

Question 21.
What is corona discharge?
Answer:
The electric field near the edge is very high and it ionizes the surrounding air. The positive ions are repelled at the sharp edge and negative ions are attracted towards the sharper edge. This reduces the total charge of the conductor near the sharp edge. This is called action at points or corona discharge.

III. Long Answer Questions:

Question 1.
Discuss the basic properties of electric charges.
Answer:
Basic properties of charges
(i) Electric charge:
Most objects in the universe are made up of atoms, which in turn are made up of protons, neutrons and electrons. These particles have mass, an inherent property of particles. Similarly, the electric charge is another intrinsic and fundamental property of particles. The SI unit of charge is the coulomb.

(ii) Conservation of charges:
Benjamin Franklin argued that when one object is rubbed with another object, charges get transferred from one to the other. Before rubbing, both objects are electrically neutral and rubbing simply transfers the charges from one object to the other. (For example, when a glass rod is rubbed against silk cloth, some negative charges are transferred from glass to silk. As a result, the glass rod is positively charged and silk cloth becomes negatively charged).

From these observations, he concluded that charges are neither created or nor destroyed but can only be transferred from one object to other. This is called conservation of total charges and is one of the fundamental conservation laws in physics. It is stated more generally in the following way. The total electric charge in the universe is constant and charge can neither be created nor be destroyed. In any physical process, the net change in charge will always be zero.

(iii) Quantisation of charges:
The charge q on any object is equal to an integral multiple of this fundamental unit of charge e.
q = ne
Here n is any integer (0, ±1, ±2, ±3, ± ….). This is called quantisation of electric charge. Robert Millikan in his famous experiment found that the value of e = 1.6 x 10^-19C. The charge of an electron is -1.6 x 10^-19 C and the charge of the proton is +1.6 x 10^-19C. When a glass rod is rubbed with silk cloth, the number of charges transferred is usually very large, typically of the order of 10¹⁰. So the charge quantisation is not appreciable at the macroscopic level. Hence the charges are treated to be continuous (not discrete). But at the microscopic level, quantisation of charge plays a vital role.

Question 2.
Explain in detail Coulomb’s law and its various aspects.
Answer:
1. Coulomb’s law states that “force of attraction or repulsion between two point charges is directly proportional to the product of the charges and inversely proportional to the square of distance between them.
\(\overrightarrow{\mathrm{F}}=\mathrm{k} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}} \hat{\mathrm{r}}_{12}\)

2. The force on the charge q₂ exerted by the charge q&lt₁ always lies along the line joining the two charges.
r̂&lt₁2 is a unit vector pointing from q₁ to q₂.

3. In SI units, \(\frac{1}{4 \pi \varepsilon_{\mathrm{o}}}\)= 9 x l0⁹Nm²C^-2
where £0 = 8.85 × 10^-12 C² N^-1m^-2 .

4. The magnitude of the electrostatic force between two charges each of one coulomb and separated by a distance of lm is
|F| = 9 x l0⁹N
This is a huge quantity, almost equivalent to weight of one million tons.

5. Coulombs law in vacuum takes the form
\(\overrightarrow{\mathrm{F}}_{21}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}} \hat{\mathrm{r}}_{12}\)
In a Medium,
\(\overrightarrow{\mathrm{F}}_{21}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}} \hat{\mathrm{r}}_{12}\)
£ > £0, the force between two point charges in a medium other than vacuum is always less than that in vacuum.

6. Relative permitivitv £r = \(\frac{\varepsilon}{\varepsilon_{o}}\)
for vacuum and air £r = 1
other media, £r > 1

Question 3.
Define ’electric field’ and discuss its various aspects.
Answer:
The electric field is defined as the force experienced by unit positive charge kept at that point.
\(\overrightarrow{\mathrm{E}}=\frac{\overrightarrow{\mathrm{F}}}{\mathrm{q}_{\mathrm{o}}}\)

Important aspects of the Electric field:

1. If the charge q is positive then the electric field points away from the source charge and if q is negative, the electric field points towards the source charge q.
2. If the electric field at a point P is E, then the force experienced by the test charge q0 placed at the point P is
   \(\overrightarrow{\mathrm{F}}=\mathrm{q}_{\mathrm{o}} \overrightarrow{\mathrm{E}}\)
3. Electric field is independent of the test charge q₀ and depends only on the source charge q.
   
4. Since the electric field is a vector quantity, at every point in space, this field has unique direction.
5. The test charge is made sufficiently small such that it will not modify the electric field of the source charge.
6. For continuous and finite size charge distributions, integration techniques must be used.
7. There are two kinds of electric field: uniform or constant electric field and non-uniform electric field.
8. Uniform electric field will have the same direction and constant magnitude at all points in space. Non-uniform electric field will have different directions or different magnitudes or both at different points in space.

Question 4.
Calculate the electric field due to a dipole on its axial line and the equatorial plane.
Answer:
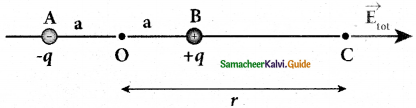
Case (i):

Electric field due to an electric dipole at points on the axial line.

1. Consider an electric dipole placed on the x-axis A point C is located at a distance of r from the midpoint of the dipole along the axial line.
   

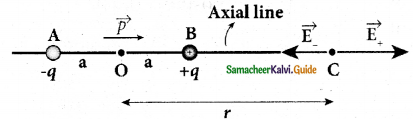
2. The electric field at a point C due to +q is
\(\overrightarrow{\mathrm{E}}_{+}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{\mathrm{q}}{(\mathrm{r}-\mathrm{a})^{2}}\) (along BC)

3. Since the electric dipole moment vector p is from -q to +q and is directed along BC, the above equation is rewritten as
\(\overrightarrow{\mathrm{E}}_{+}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{\mathrm{q}}{(\mathrm{r}-\mathrm{a})^{2}} \hat{\mathrm{p}}\) ………..(1)

4. The electric field at a point C due to -q is
\(\overrightarrow{\mathrm{E}}_{-}=-\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{\mathrm{q}}{(\mathrm{r}+\mathrm{a})^{2}} \hat{\mathrm{p}}\) ……………(2)

5. Since +q is located closer to the point C than -q, \(\overrightarrow{\mathrm{E}}+\) is stronger than \(\overrightarrow{\mathrm{E}}_{-}\).
Therefore, the length of the \(\overrightarrow{\mathrm{E}}+\) vector is drawn larger than that of \(\overrightarrow{\mathrm{E}}_{-}\) vector.
The total electric field at point C is calculated using the superposition principle of the electric field.

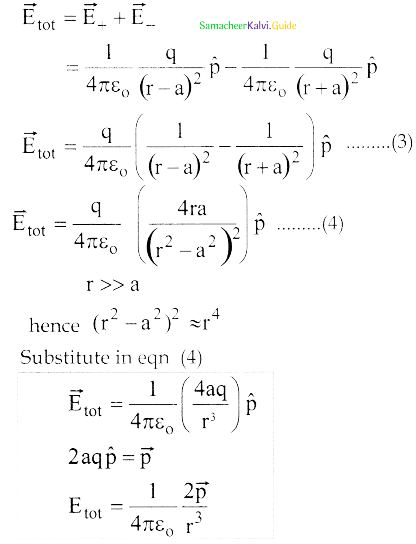
6. The direction of is shown in Figure

Case (ii)
1. Electric field due to an electric dipole at a point on the equatorial plane

2. Consider a point C at a distance r from the midpoint 0 of the dipole on the equatorial plane.

3. Since point C is equidistant from +q and -q and are the same.

4. The direction of \(\overrightarrow{\mathrm{E}}+\) is along BC and the direction of \(\overrightarrow{\mathrm{E}}_{-}\) is along CA.

\(\overrightarrow{\mathrm{E}}+\) and \(\overrightarrow{\mathrm{E}}_{-}\) are resolved into two components; one component parallel to the dipole axis and the other perpendicular to it.

5. The perpendicular components \(|\overrightarrow{\mathrm{E}}|\) sinθ and \(\left|\overrightarrow{\mathrm{E}}_{-}\right|\) sinθ are oppositely directed and cancel each other.
\(\mathrm{E}_{\text {tot }}=-\left|\mathrm{E}_{+}\right| \cos \theta \hat{\mathrm{p}}-\left|\overrightarrow{\mathrm{E}}_{-}\right| \cos \theta \hat{\mathrm{p}} \cdots \ldots .(6)\)

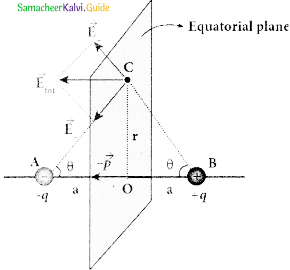
6. The magnitudes \(\overrightarrow{\mathrm{E}}+\) and \(\overrightarrow{\mathrm{E}}_{-}\) are the same and are given by

7. By substituting equation (7) into equation (6) we get
\(\overrightarrow{\mathrm{E}}_{\mathrm{tot}}=-\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{2 \mathrm{q} \cos \theta}{\left(\mathrm{r}^{2}+\mathrm{a}^{2}\right)} \hat{\mathrm{p}}\)
since \(\cos \theta=\frac{a}{\sqrt{r^{2}+a^{2}}}\)

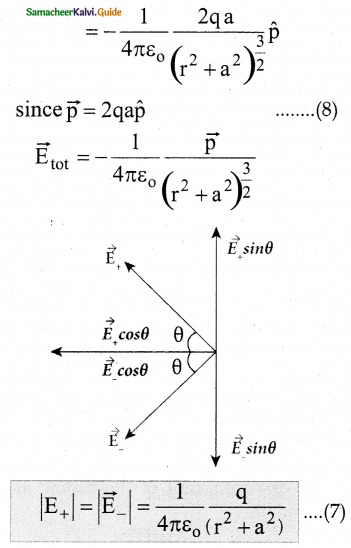
8. At very large distances (r»a), the equation (8) becomes
\(\overrightarrow{\mathrm{E}}_{\mathrm{tot}}=-\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{\overrightarrow{\mathrm{p}}}{\mathrm{r}^{3}}(\mathrm{r}>>\mathrm{a})\)

Question 5.
Derive an expression for the torque experienced by a dipole due to a uniform electric field.
Answer:
1. Consider an electric dipole of dipole moment \(\overrightarrow{\mathrm{p}}\) placed in a uniform electric field . The charge+q will experience a force q\(\overrightarrow{\mathrm{E}}\) in the direction of the field and charge-q\(\overrightarrow{\mathrm{E}}\) will experience a force -qE in a direction opposite to the field. Since the external field \(\overrightarrow{\mathrm{E}}\) is uniform, the total force acting on the dipole is zero.

2. These two forces acting at different points will constitute a couple and the dipole experience a torque. This torque tends to rotate the dipole.

3. The total torque on the dipole about the point 0, is given by
\(\vec{\tau}=\overrightarrow{\mathrm{0A}} \times(-\mathrm{q} \overrightarrow{\mathrm{E}})+\overrightarrow{\mathrm{0B}} \times \mathrm{q} \overrightarrow{\mathrm{E}}\)
Torque on dipole.

4. Total torque is perpendicular to the plane of the paper and is directed into it. The magnitude of the total torque
\(\vec{\tau}=|\overrightarrow{\mathrm{0A}}|(-\mathrm{q} \overrightarrow{\mathrm{E}})|\sin \theta+| \overrightarrow{\mathrm{0B}}|\mathrm{q} \overrightarrow{\mathrm{E}}| \sin \theta\)

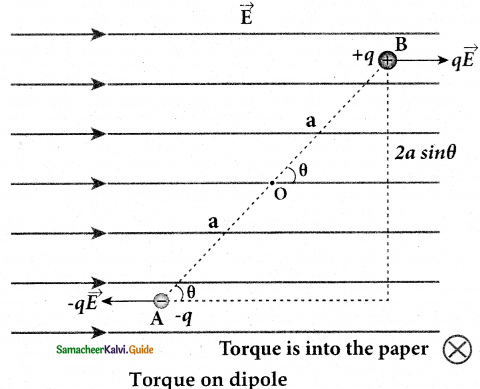
\(\tau\) = qE.2a sin θ

5. Where θ is the angle made by \(\overrightarrow{\mathrm{p}}\) with \(\overrightarrow{\mathrm{E}}\). Since p = 2aq, the torque is written in terms of the vector product as
\(\vec{\tau}=\overrightarrow{\mathrm{p}} \times \overrightarrow{\mathrm{E}}\)

6. The magnitude of thectrque is \(\tau=p E \sin \theta\) and is maximum when θ = 90^o.
This torque tends to rotate the dipole and align it with the electric field \(\overrightarrow{\mathrm{E}}\). once \(\overrightarrow{\mathrm{p}}\) is aligned with, the total torque on the dipole becomes zero.

7. If the electric field is nonuniform, then the force experienced by +q is different from that experienced by -q. In addition to the torque, there will be a net force acting on the dipole.

Question 6.
Derive an expression for electrostatic potential due to a point charge.
Answer:
1. Consider a positive charge ‘q’ kept fixed at the origin. Let P be a point at distance r from the charge ‘q’.

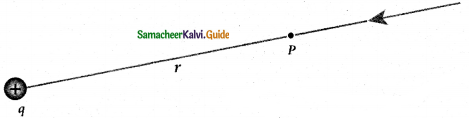
2. The electric potential at the point P is
\(\mathrm{V}=\int_{\infty}^{\mathrm{r}}(-\overrightarrow{\mathrm{E}}) \cdot \mathrm{d} \overrightarrow{\mathrm{r}}=-\int_{\infty}^{\mathrm{r}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{dr}}\)

3. Electric field due to positive point charge is
\(\begin{array}{l}
\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{\mathrm{q}}{\mathrm{r}^{2}} \hat{\mathrm{r}} \\
\mathrm{V}=\frac{-1}{4 \pi \varepsilon_{\mathrm{o}}} \int_{\infty}^{\mathrm{r}} \frac{\mathrm{q}}{\mathrm{r}^{2}} \hat{\mathrm{r}} \cdot \mathrm{d} \overrightarrow{\mathrm{r}}
\end{array}\)

4. The infinitesimal displacement vector,
d\(\overrightarrow{\mathrm{r}}\) = drr̂ and using r̂.r̂ = 1, we have
\(\mathrm{V}=\frac{-1}{4 \pi \varepsilon_{\mathrm{o}}} \int_{\infty}^{\mathrm{r}} \frac{\mathrm{q}}{\mathrm{r}^{2}} \hat{\mathrm{r}} \cdot \mathrm{dr} \hat{\mathrm{r}}=-\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \int_{\infty}^{\mathrm{r}} \frac{\mathrm{q}}{\mathrm{r}^{2}} \mathrm{dr}\)

5. After the integration,
\(\mathrm{V}=-\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \mathrm{q}\left\{-\frac{1}{\mathrm{r}}\right\}_{\infty}^{\mathrm{r}}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{\mathrm{q}}{\mathrm{r}}\)

6. Hence the electric potential due to a point charge q at a distance r is
\(\mathrm{V}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{\mathrm{q}}{\mathrm{r}}\)

Question 7.
Derive an expression for electrostatic potential due to an electric dipole.
Answer:
Consider two equal and opposite charges separated by a small distance 2a. The point P is located at a distance r from the midpoint of the dipole. Let θ be the angle between the line OP and dipole axis AB.

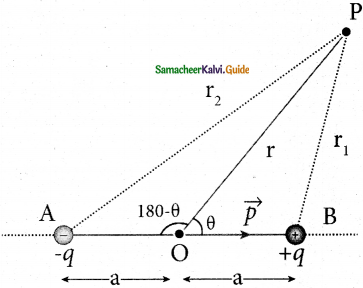
Potential due to electric dipole:
1. Let r₁ be the distance of point P from +q and r₂ be the distance of point P from -q.

2. Potential at P due to charge,
\(+q=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r_{1}}\)
Potential at P due to charge
\(-q=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{r_{2}}\)
Total potential at the point P,
\(\mathrm{V}=\frac{\mathrm{q}}{4 \pi \varepsilon_{\mathrm{o}}}\left(\frac{1}{\mathrm{r}_{1}}-\frac{1}{\mathrm{r}_{2}}\right)\) (1)

3. By the cosine law for triangle BOP,
r₁² =r² + a² – 2ra cos θ

4. Similarly applying the cosine law for triangle A0P,
r₂² = r² + a²  – 2racos(180-θ)
since cos(180-θ) = – cos θ
r₂² = r² + a² +2racos θ

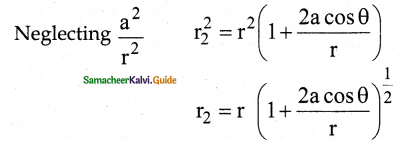
Using Binomial theorem, we get

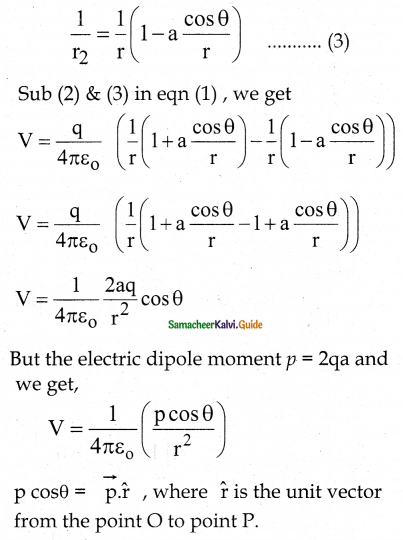
\(\mathrm{V}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{\overrightarrow{\mathrm{p}} \cdot \hat{\mathrm{r}}}{\mathrm{r}^{2}}\)
Special Cases:

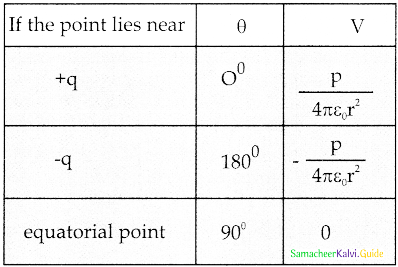
Question 8.
0btain an expression for potential energy due to a collection of three-point charges which are separated by finite
distances.
Answer:

1. The electric potential at a point at a distance r from point charge q&lt₁ is given by
   \(\mathrm{V}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{\mathrm{q}_{1}}{\mathrm{r}}\)
2. The potential V is the work done to bring a unit positive charge front infinity to the point. If the charge q, is brought from infinity to that point at a distance r from q₁.
3. The work done is stored as the electrostatic potential energy W = q₂V
   \(\mathrm{U}=\mathrm{q}_{2} \mathrm{~V}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \mathrm{q}_{1} \mathrm{q}_{2}\) ………….(1)
4. The electrostatic potential energy depends only on the distance between the two point charges.

Three charges are arranged in the following configuration.

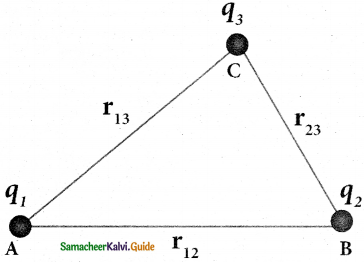
1. Bringing a charge q₁ from infinity to point A requires no work because there are no other charges already present in the vicinity of charge q₁.

2. To bring the second charge q₂ to point B, work must be done against the electric field at B created by the charge q₁. So the work done on the charge q₂ is Wq₂V_1B Here V_1B is electrostatic potential due to the charge q₁ at point B.
\(\mathrm{U}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}_{12}}\) (2)

3. Similarly to bring the charge q₂ to point C, work has to be done against the total electric field due to both the charges q₁ and q₂. So the work done to bring the charge q₃ is the electrostatic potential due to charge q₁ at point C and V₂ is the electrostatic potential due to charge q₂ at point C. The electrostatic potential is
\(\mathrm{U}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}}\left(\frac{\mathrm{q}_{1} \mathrm{q}_{3}}{\mathrm{r}_{13}}+\frac{\mathrm{q}_{2} \mathrm{q}_{3}}{\mathrm{r}_{23}}\right)\) ………….(3)

4. Adding equations (2) and (3), the total electrostatic potential energy for the system of three charges q₁, q₂ and q₃ is
\(\mathrm{U}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}}\left(\frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}_{12}}+\frac{\mathrm{q}_{1} \mathrm{q}_{3}}{\mathrm{r}_{13}}+\frac{\mathrm{q}_{2} \mathrm{q}_{3}}{\mathrm{r}_{23}}\right)\) ……………. (4)

Question 9.
Derive an expression for the electrostatic potential energy of the_dipole in a uniform electric field.
Answer:
1. Consider a dipole placed in the uniform electric field \(\overrightarrow{\mathrm{E}}\). A dipole experiences a torque when kept in an uniform electric field \(\overrightarrow{\mathrm{E}}\). This torque rotates the dipole to align it with the direction of the electric field.

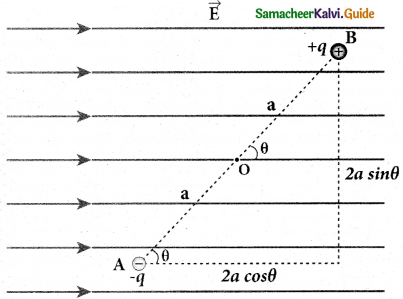
2. To rotate the dipole an equal and opposite external torque must be applied on the dipole.

3. The work done by the external torque to rotate the dipole from angle θ<super>1 to θ at constant angular velocity is

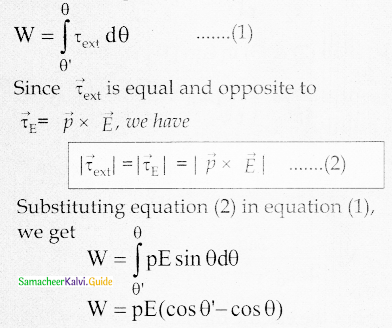
4. The work done is equal to the potentiaL energy difference between the angular positions θ’ and θ.
U(θ) – U(θ’)= ΔU = – pE cos θ+pE cos θ’

5. If the initial angle is θ’ = 90° and is taken as reference point, then U(θ’)= pE cos 90°=0.

6. The potential energy stored in the system of dipole kept in the uniform electric field is given by
U= – pE cos θ = – \(\overrightarrow{\mathrm{p}}\).\(\overrightarrow{\mathrm{E}}\) ……….(3)

7. In addition to p and E, the potential energy also depends on the orientation 0 of the electric dipole with respect to the external electric field.

8. The potential energy is maximum when the dipole is aligned anti-parallel (θ = π) to the external electric field and minimum when the dipole is aligned parallel (θ = 0)

Question 10.
Obtain Gauss law from Coulomb’s law.
Answer:
1. Consider a positive point charge Q is surrounded by an imaginary sphere of radius r.

2. The total electric flux for the entire area is given by,
\(\Phi_{\mathrm{E}}=\oint \mathrm{E} \cdot \mathrm{d} \overrightarrow{\mathrm{A}}=\oint \mathrm{EdA} \cos \theta \ldots \ldots\) (1)

3. The electric field of the point charge is directed radially outward at all points on the surface of the sphere. Therefore the direction of the area element d\(\overrightarrow{\mathrm{A}}\) is along the electric field \(\overrightarrow{\mathrm{E}}\) and θ = 0°.
\(\Phi_{\mathrm{E}}=\oint \mathrm{E.dA}\) (since cos 0° = 1)
E is a uniform on the surface of the sphere

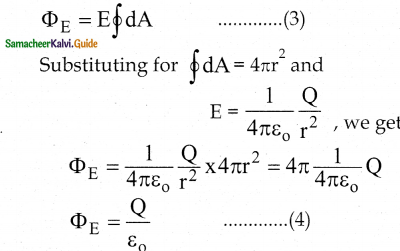
4. This equation is Gauss Law.

Question 11.
Obtain the expression for electric field due to an infinitely long charged wire.
Answer:

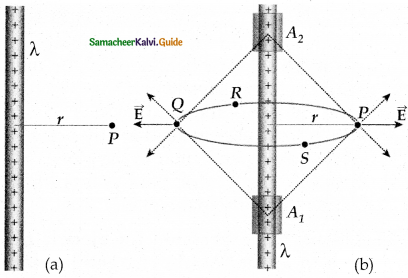
Electric field due to infinite long charged wire:

1. Consider an infinitely long straight wire having uniform linear charge density λ.

2. Let P be a point located at a perpendicular distance r for the wire.

3. The charged wire possesses a cylindrical symmetry.

4. Let us choose a cylindrical Gaussian surface of radius r and length L,

5. The total electric flux in this closed surface is calculated as follows.

for the curved surface. \(\overrightarrow{\mathrm{E}}\) is parallel to \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{E}}\) .dA = EdA.
For the top and bottom surfaces,
\(\overrightarrow{\mathrm{E}}\) is perpendicular to \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{E}}\)
\(\begin{aligned}
&\Phi_{\mathrm{E}}=\int_{\text {Curved }} \mathrm{EdA}=\frac{\mathrm{Q}_{\text {encl }}}{\varepsilon_{0}} \ldots \ldots . \text { (2) }\\
&\text { surface }
\end{aligned}\)

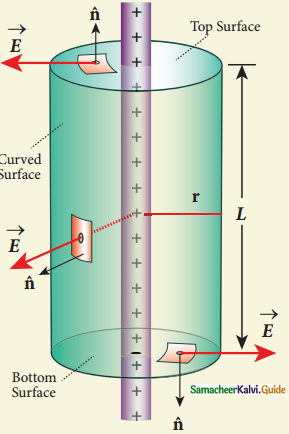
Since the electric field is constant, E is taken out of the integration and
Q_encl is given by Q_encl=λL.
E \(\int_{\begin{array}{l}
\text { Curved } \\
\text { surface }
\end{array}} \mathrm{d} \mathrm{A}=\frac{\lambda \mathrm{L}}{\varepsilon_{\mathrm{o}}}\) ……..(3)
Here,
Φ_E=∫_{curved surface} dA= total area of the curved surface = 2πrL
E.2πrL=\(=\frac{\lambda \mathrm{L}}{\varepsilon_{\mathrm{o}}}\)

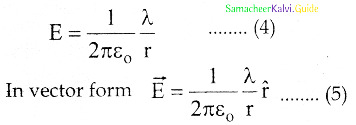
6. The electric field due to the infinite charged wired depends on \(\frac{1}{\mathrm{r}}\)rather than \(\frac{1}{r^{2}}\) for a point charge.

7. Equation (5) indicates that the electric field is always along the perpendicular direction (r̂) to wire. If λ > 0 then \(\overrightarrow{\mathrm{E}}\) points perpendicular outward (r̂) from the wire and if λ < 0, then points perpendicular inward (-r̂).

Question 12.
Obtain the expression for electric field due to a charged infinite plane sheet.
Answer:

1. Consider an infinite plane sheet of charges with uniform surface charge density σ.
2. Let P be a point at a distance of r from the sheet.

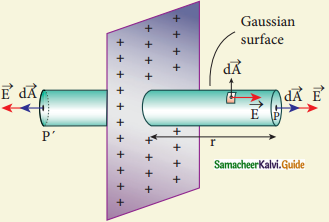
Electric field due to changed infinite Planar sheet:

1. A cylindrical shaped Gaussian surface of length 2r and area A of the flat surfaces are chosen such that the infinite plane sheet passes perpendicularly through the middle part of the Gaussian surface.
2. Applying Gauss law for this cylindrical surface.
   
3. n̂ is the outward unit vector normal to the plane. The electric field depends on the surface charge density and is independent of the distance r.
4. If σ > 0, the electric field at any point P is outward perpendicular to the plane.
5. If σ < 0, the electric field points inward perpendicularly to the plane.

Question 13.
Obtain the expression for electric field due to a uniformly charged spherical shell.
Answer:
Consider a uniformly charged spherical shell of radius R and total charge Q.
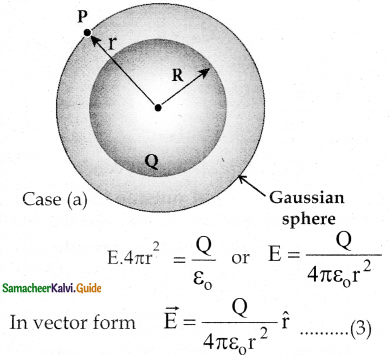
Case (a) At a point outside the shell (r > R)
1. Let us choose a point P outside the shell at a distance r from the center.

2. The charge is uniformly distributed on the surface of the sphere.

3. The electric field must point radially outward if Q > 0 and point radially inward if Q < 0.

4. A spherical Gaussian surface of radius r is chosen and the total charge enclosed by this Gaussian surface is Q.

5. By Gauss law.
\(\oint_{\text {Gaussian }} \overrightarrow{\mathrm{E}} \cdot \mathrm{d} \overrightarrow{\mathrm{A}}=\frac{\mathrm{Q}}{\varepsilon_{\mathrm{o}}}\) ………..(1)

6. The magnitude of is also the same at all points due to the spherical symmetry of the charge distribution.
\(\mathrm{E} \oint_{\text {Gaussian }} \mathrm{d} \mathrm{A}=\frac{\mathrm{Q}}{\varepsilon_{\mathrm{o}}}\) ………….(2)

7. The total area of the Gaussian surface,
∫dA = 4πr²
E.4πr²=\(\frac{\mathrm{Q}}{\varepsilon_{\mathrm{o}}}\)
For points outside the sphere, a large spherical Gaussian surface is drawn concentric with the sphere.

8. For points outside the sphere, a spherical gaussian surface smaller than the sphere is drawn

Case (c):
The electric field due to a charged spherical cell

• The electric field is radially outward if Q > 0 and radially inward if Q < 0.

Case (b):
At a point on the surface of the spherical shell (r=R)

• The electrical field at points on the spherical shell (r=R) is given by
  
  Electric fields versus distance Gauss spherical shell of radius R

Case (c):
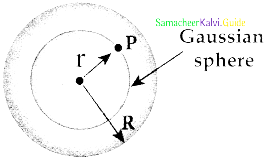
At point inside the spherical shell (r < R)

1. Consider a point P inside the shell at a distance r from the center.
2. A Gaussian sphere of radius r is constructed.
3. Applying Gauss law,
   \(\begin{aligned}
   &\oint_{\text {Gaussian }} \overrightarrow{\mathrm{E}} \cdot \mathrm{d} \overrightarrow{\mathrm{A}}=\frac{\mathrm{Q}}{\varepsilon_{\mathrm{o}}}\\
   &\mathrm{E} .4 \pi \mathrm{r}^{2}=\frac{\mathrm{Q}}{\varepsilon_{\mathrm{o}}}
   \end{aligned}\) …………..(5)
4. Since Gaussian surface encloses no charge, Q = 0.
   E = 0 ……………(6)
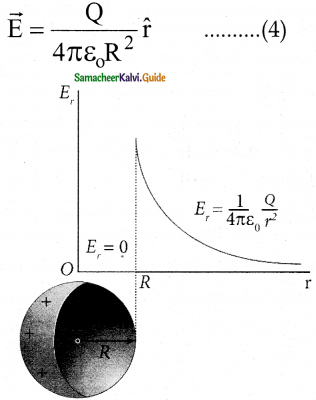
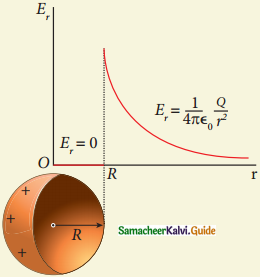   Electric field versus distance for a spherical shell of radius R
5. The electric field due to the uniformly charged spherical shell is zero at all points inside the shell.
6. A graph can be plotted between the electric field and radial distance.

Question 14.
Discuss the various properties of conductors in electrostatic equilibrium,
i) The electric field is zero everywhere, inside the conductor. This is true regardless of whether the conductor is solid or hollow.
Answer:

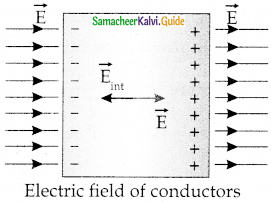
1. When we apply a uniform electric field, the free electrons accelerated.
2. It causes the left side to be negatively charged and the right side to be positively charged.
3. Due to this realignment of free electrons, there will be an internal electric field created inside the conductor.
4. It increases until it nullifies the external electric field and is said to be in electrostatic equilibrium in the order of
   10^-16 s.
   

ii) There is no net charge inside the conductors. The charges must reside only on the surface of the conductors.

1. Consider an arbitrarily shaped conductor and a Gaussian surface is drawn inside the conductor.
2. It is very close to the surface of the conductor.
3. Since the electric field is zero inside the conductor, the net electric flux is zero.
4. So, there is no net charge inside the conductor.
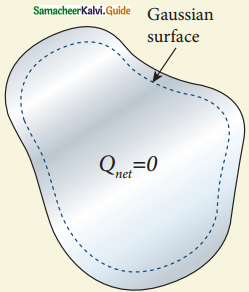5. No net charge inside the conductor

iii) The electric field outside the conductor is perpendicular to the surface of the conductor and has a magnitude of σ/ε. Where σ is the surface charge density at that point.

1. If the electric field has components parallel to the surface of the conductor, then free electrons of the surface of the conductor ‘would experience acceleration.
   
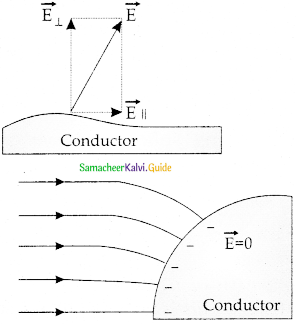
   (a) Electric field is along the surface
   (b) Electric field is perpendicular to the surface of the conductor
2. At electrostatic equilibrium, the electric field must be perpendicular to the surface of the conductor.
3. Consider a small cylindrical gaussian surface. 0ne half of this cylinder is embedded inside the conductor.
   
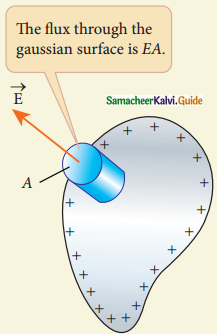
4. Since the electric field is normal to the surface of the conductor, the curved part of the cylinder has zero electric flux.
5. Inside the conductor, the electric field is zero.
6. The bottom flat part of the Gaussian surface has no electric flux.
7. The top flat part of the Gaussian surface contributes to the electric flux.
8. The electric field is parallel to the area vector and the total charge inside the surface is σA.
9. Applying Gauss law, EA = \(\frac{\sigma \mathrm{A}}{\varepsilon_{\mathrm{o}}}\)
10. In Vector form, \(\overrightarrow{\mathrm{E}}\)=\(\frac{\sigma}{\varepsilon_{\mathrm{o}}} \hat{\mathrm{n}}\)

iv) The electrostatic potential has the same value on the surface and inside of the conductor.

1. This is possible only if the electrostatic potential is constant at all points on the surface and there is no potential difference between any two points on the surface.
2. Since the electric field is zero inside the conductor, the potential is the same as the surface of the conductor.
3. At electrostatic equilibrium, the conductor is always at equipotential.

Question 15.
Explain the process of electrostatic induction.
Answer:
Definition: Charging without actual contact is called electrostatic induction.

Consider an uncharged (neutral) conducting sphere at rest on an insulating stand. A negatively charged rod is brought near the conductor without touching. (Fig. a)

1. The negative charge of the rod repels the electrons in the conductor to the opposite side. As a result, positive charges are induced near the region of the charged rod while negative charges on the farther side.
2. Before introducing the charged rod, the free electrons were distributed uniformly on the surface of the conductor and the net charge is zero. 0nce the charged rod is brought near the conductor, the distribution is no longer uniform with more electrons located on the farther side of the rod and positive charges are located closer to the rod. But the total charge is zero.

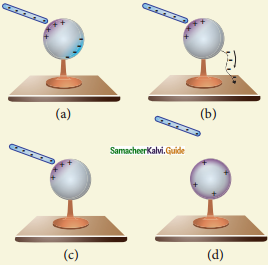
Now the conducting sphere is connected to the ground through a conducting wire, This is called grounding. Since the ground can always receive any amount of electrons, grounding removes the electron from the conducting sphere.
(Fig. b)

3. When the grounding wire is removed from the conductor, the positive charges remain near the charged rod.
(Fig. c)

4. Now the charged rod is taken away from the conductor. As soon as the charged rod is removed, the positive charge gets distributed uniformly on the surface of the conductor. By this process, the neutral conducting sphere becomes positively charged. (Fig. d)

Question 16.
Explain the dielectrics in detail and how an electric field is induced inside a dielectric.
Answer:

1. When an external electric field is applied to a conductor, the charges are aligned in such a way that an internal electric field is created which cancels the external electric field.
2. But in the case of a dielectric, which has no free electrons, the external electric field only realigns the charges so that an internal electric field is produced.
3. The magnitude of the internal electric field is smaller than that of the external electric field.
4. Therefore the net electric field inside the dielectric is not zero but is parallel to an external electric field with a magnitude less than that of the external electric field.
5. For example, let us consider a rectangular dielectric slab placed between two oppositely charged plates (capacitor).
   a)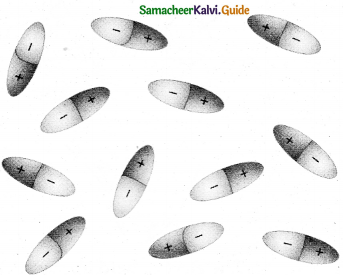

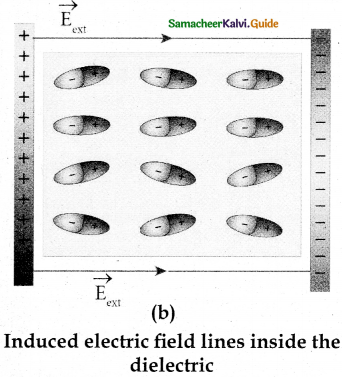
1. The uniform electric field between the plates acts as an external electric field ext which polarizes the dielectric placed between plates.
2. The positive charges are induced on one side surface and negative charges are induced on the other side of the surface.
3. But inside the dielectric, the net charge is zero even in a small volume.
4. So the dielectric in the external field is equivalent to two oppositely charged sheets with the surface charge densities
   +σ_b and -σ_b.
5. These charges are called bound charges. They are not free to move like free electrons in conductors.

Question 17.
0btain the expression for capacitance for a parallel plate capacitor.
Answer:

1. Consider a capacitor with two parallel plates each of cross-sectional area A and separated by a distance d.
2. The electric field between two infinite parallel plates is uniform and is given by
   \(\mathrm{E}=\frac{\sigma}{\varepsilon_{\mathrm{o}}}\)
   \(\sigma=\frac{Q}{A}\)
   σ = surface charge density on the plates
   
   
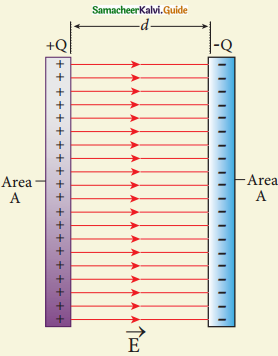
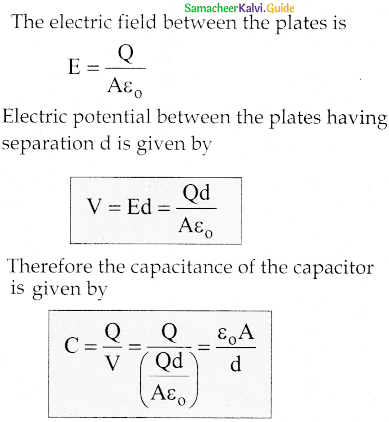
3. Capacitance is directly proportional to the area of cross-section and is inversely proportional to the distance between the plates.
4. If the area of cross-section of the capacitor plates is increased, more charges can be distributed for the same potential difference. As a result, the capacitance is increased.
5. If the distance between the two plates is reduced, the potential difference between the plate decreases with the E constant.
6. The voltage difference between the terminals of the battery increases, leads to an additional flow of charge to the plates from the battery, till the voltage on the capacitor equals the battery’s terminal voltage.
7. If the distance is increased, the capacitor voltage increases and becomes greater than the battery voltage.
8. The charges flow from capacitor plates to the battery till both voltages become equal.

Question 18.
0btain the expression for energy stored in the parallel plate capacitor.
Answer:

1. Capacitor not only stores the charge but also stores energy.
2. When a battery is connected to the capacitor, electrons of total charge -Q are transferred from one plate to the other plate.
3. To transfer the charge, work is done by the battery. This work done is stored as electrostatic potential energy in the capacitor.
4. To transfer an infinitesimal charge dQ for a potential difference V, the work done is given by
   dW = V dQ ………….(1)
   
5. This stored energy is thus directly proportional to the capacitance of the capacitor and the square of the voltage between the plates of the capacitor.
   \(\mathrm{U}_{\mathrm{E}}=\frac{1}{2}\left(\frac{\varepsilon_{\mathrm{o}} \mathrm{A}}{\mathrm{d}}\right)(\mathrm{Ed})^{2}=\frac{1}{2} \varepsilon_{\mathrm{o}}(\mathrm{Ad}) \mathrm{E}^{2}\) …………(4) where Ad = volume of the space between the capacitor plates. The energy stored per unit volume of space is defined \(\mathrm{U}_{\mathrm{E}}=\frac{1}{2} \varepsilon_{\mathrm{o}} \mathrm{E}^{2}\) ……….(5)
6. Energy is stored in the electric field existing between the plates of the capacitor. 0nce the capacitor is allowed to discharge, the energy is retrieved.
7. The energy density depends only on the electric field and not on the size of the plates of the capacitor.

Question 19.
Explain in detail the effect of a dielectric placed in a parallel plate capacitor.
Answer:

1. Consider a capacitor with two parallel plates each of cross-sectional area A and are separated by distance d.
2. The capacitor is charged by a battery of voltage V₀ and the charge stored is Q₀
3. The capacitance of the capacitor without the dielectric is
   \(\mathrm{C}_{\mathrm{0}}=\frac{\mathrm{Q}_{\mathrm{0}}}{\mathrm{V}}\)

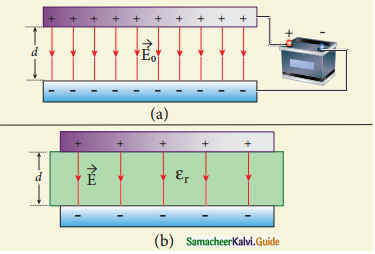
1. The modified electric field is,
   \(\mathrm{E}=\frac{\mathrm{E}_{\mathrm{o}}}{\varepsilon_{\mathrm{r}}} \ldots \ldots \ldots .(1)\)
2. Here E₀ is the electric field inside the capacitors when there is no dielectric and
   Er is the dielectric constant. Since εr >1, the electric E < E₀.
3. As a result, the electrostatic potential difference between the plates (V = Ed) is also reduced. But at the same time, the charge Q₀ will remain constant once the battery is disconnected.
4. Hence the new potential difference is,
   \(\mathrm{V}=\mathrm{Ed}=\frac{\mathrm{E}_{0}}{\varepsilon_{\mathrm{r}}} \mathrm{d}=\frac{\mathrm{V}_{\mathrm{o}}}{\varepsilon_{\mathrm{r}}}\) …………(2)
5. Thus new capacitance in the presence of a dielectric is,
   \(\mathrm{C}=\frac{\mathrm{Q}_{\mathrm{o}}}{\mathrm{V}}=\varepsilon_{\mathrm{r}} \frac{\mathrm{Q}_{\mathrm{o}}}{\mathrm{V}_{\mathrm{o}}}=\varepsilon_{\mathrm{r}} \mathrm{C}_{\mathrm{o}}\) ……………..(3)
   Since ε_r > 1, we have C > C₀ . Thus insertion of the dielectric constant ε_r increases the capacitance.
   \(\mathrm{C}=\frac{\varepsilon_{\mathrm{r}} \varepsilon_{\mathrm{o}} \mathrm{A}}{\mathrm{d}}=\frac{\varepsilon \mathrm{A}}{\mathrm{d}}\) ……………(4)
   where ε = ε_r ε₀ is the permititivity of the dielectric medium.
6. The energy stored in the capacitor before the insertion of a dielectric is given by
   \(\mathrm{U}_{\mathrm{o}}=\frac{1}{2} \frac{\mathrm{Q}_{0}^{2}}{\mathrm{C}_{0}}\) ………(5)
7. After the dielectric is inserted, Q₀ remains constant but the capacitance is increased.
8. The stored energy is decreased.
9. \(\mathrm{U}_{\mathrm{o}}=\frac{1}{2} \frac{\mathrm{Q}_{0}^{2}}{\mathrm{C}_{0}}=\frac{1}{2} \frac{\mathrm{Q}_{0}^{2}}{\varepsilon_{\mathrm{r}} \mathrm{C}_{0}}=\frac{\mathrm{U}_{\mathrm{o}}}{\varepsilon_{\mathrm{r}}}\) ………………..(6)
   Since ε_r > 1, we get U > U₀.

ii) When the battery remains connected to the capacitor:

1. The battery of voltage V₀ remains connected to the capacitor when the dielectric is inserted into the capacitor.
2. The potential difference V₀ across the plates remains constant.
3. The charge stored in the capacitor is increased by a factor ε_r.
   
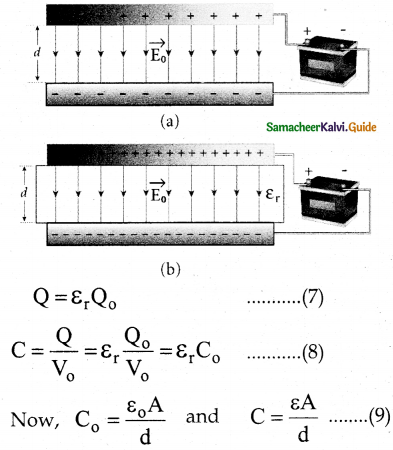
4. The energy stored in the capacitor before the insertion of a dielectric is given by \(\mathrm{U}_{\mathrm{o}}=\frac{1}{2} \mathrm{C}_{\mathrm{o}} \mathrm{V}_{\mathrm{o}}^{2}\) ………..(10)
5. After the dielectric is inserted, the capacitance is increased and the stored energy is also increased
6. \(\mathrm{U}=\frac{1}{2} \mathrm{CV}_{\mathrm{o}}^{2}=\frac{1}{2} \varepsilon_{\mathrm{r}} \mathrm{C}_{\mathrm{o}} \mathrm{V}_{\mathrm{o}}^{2}=\varepsilon_{\mathrm{r}} \mathrm{U}_{\mathrm{o}}\) …………(11)
   Since ε_r>1 we have U > U₀.
7. Since the voltage between capacitor V, is constant, the electric field between the plates also remains constant.
8. The energy density is given by
   \(\mathrm{U}=\frac{1}{2} \varepsilon \mathrm{E}_{0}^{2}\) (12)
   where ε is the permittivity of the given dielectric material.

Question 20.
Derive the expression for resultant capacitance, when capacitors are connected in series and in parallel.
Answer:
i) Capacitor in series

1. Consider three capacitors of capacitance C₁, C_2, and C₃
2. connected in series with a battery of voltage V.
   
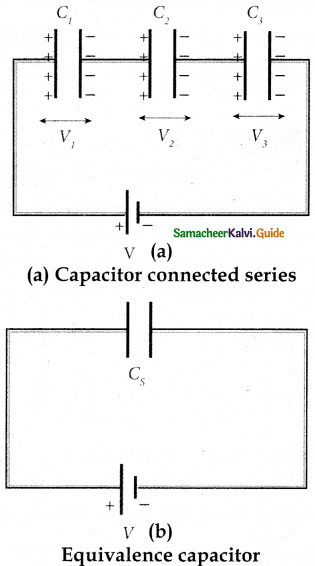
3. By these processes, each capacitor stores the same amount of charge Q. The capacitances of the capacitors are in general different so that the voltage across each capacitor is also different and are denoted as V₁, V₂ and V₃ respectively.
4. The total voltage across each capacitor must be equal to the voltage of the battery.
   V = V₁ + V₂ + V₃
5. Since, Q = CV, we have \(\mathrm{V}=\frac{\mathrm{Q}}{\mathrm{C}_{1}}+\frac{\mathrm{Q}}{\mathrm{C}_{2}}+\frac{\mathrm{Q}}{\mathrm{C}_{3}}\)
   \(\mathrm{V}=\mathrm{Q}\left(\frac{1}{\mathrm{C}_{1}}+\frac{1}{\mathrm{C}_{2}}+\frac{1}{\mathrm{C}_{3}}\right)\)
   \(\frac{\mathrm{Q}}{\mathrm{C}_{\mathrm{s}}}=\mathrm{Q}\left(\frac{1}{\mathrm{C}_{1}}+\frac{1}{\mathrm{C}_{2}}+\frac{1}{\mathrm{C}_{3}}\right), \frac{1}{\mathrm{C}_{\mathrm{s}}}=\frac{1}{\mathrm{C}_{1}}+\frac{1}{\mathrm{C}_{2}}+\frac{1}{\mathrm{C}_{3}}\)
6. The inverse of the equivalent capacitance C_s of three capacitors connected in series is equal to the sum of the inverses of each capacitance.
7. The equivalent capacitance C_s is always less than the smallest individual capacitance in the series.

ii) Capacitance in parallel:

1. Consider three capacitors of capacitance C₁, C_2, and C₃ connected in parallel with a battery of voltage V.
2. The potential difference across each capacitor is the same.
   Total charge Q = Q₁ + Q₂ + Q₃
   Q₁, Q2, Q3 – Charge stored in C₁, C₂, C₃
   Now, since Q = CV, we have Q = C₁V + C₂V + C₃V
   
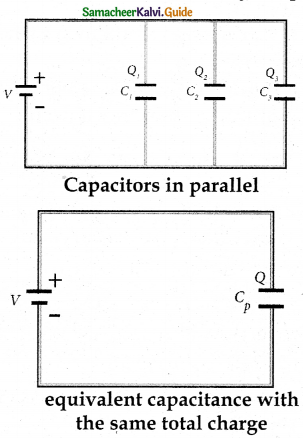
3. If these three capacitors are considered to form a single capacitance Cp which stores the total charge Q.
   Q = C_pV.
   C_pV= C₁V + C₂V + C₃V
   C_p = C₁ + C₂ + C₃
4. The equivalent capacitance of capacitors connected in parallel is equal to the sum of the individual capacitances.
5. The equivalent capacitance C_p in a parallel connection is always greater than the largest individual capacitance.

Question 21.
Explain in detail how charges are distributed in a conductor, and the principle behind the lightning conductor.
Answer:
1. Consider two conducting spheres A and B of radii r₁ and r₂ respectively connected to each other by a thin conducting wire.

2. If a charge Q is introduced into any one of the spheres, this charge Q is redistributed into both the spheres such that the electrostatic potential is the same in both the spheres.

3. They are now uniformly charged and attain electrostatic equilibrium.

4. Let q₁ be the charge residing on the surface of sphere A and is the charge residing on the surface of sphere B such that, Q = q₁ + q₂.

5. The charges are distributed only on the surface and there is no net charge inside the conductor.

6. The electrostatic potential at the surface of the sphere A is given by
\(V_{A}=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1}}{r_{1}}\)

7. The electrostatic potential at the surface of the sphere B is given by 1 q₂
\(V_{B}=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{2}}{r_{2}}\)
V_A = V_B

\(\frac{\mathrm{q}_{1}}{\mathrm{r}_{1}}=\frac{\mathrm{q}_{2}}{\mathrm{r}_{2}}\)

8. The charge density on the surface of sphere A is σ₁, and the charge density on the surface of sphere B is σ₂. This implies that q₁ = 4πr₁² σ₁ and

q₂ = 4πr₂² σ₂ ………..(3)
σ₁r₁ = σ₂r₂ ………..(4)
σr = constant ………..(5)

9. The surface charge density σ is inversely proportional to the radius of the sphere.
Corona discharge:

Consider a charged conductor of irregular shape.

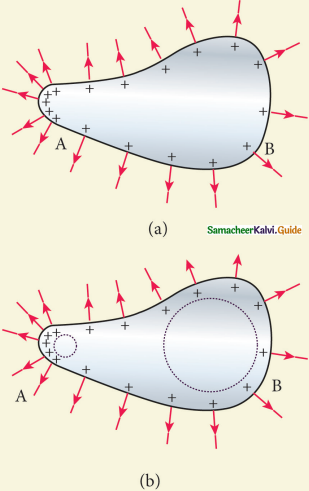
10. The smaller the radius of curvature, the larger is the charge density. The end of the conductor which has larger curvature (smaller radius) has a large charge accumulation.

11. As a result, the electric field near this edge is very high and it ionizes the surrounding air. The positive ions are repelled at the sharp edge and negative ions are attracted towards the sharper edge.

12. This reduces the total charge of the conductor near the sharp edge. This is called action at points or corona discharge.

Lightning conductor:
Uses to protect tall buildings from lightning strikes.

Principle:
Action at points or corona discharge.

Construction:

1. This device consists of a long thick copper rod passing from the top of the building to the ground.
2. The upper end of the rod has a sharp spike or a sharp needle.
3. The lower end of the rod is connected to the copper plate which is buried deep into the ground.

Working:

1. When a negatively charged cloud is passing above the building, it induces a positive charge on the spike.
2. Since the induced charge density on a thin sharp spike is large, it results in a corona discharge.
3. This positive charge ionizes the surrounding air which in turn neutralizes the negative charge in the cloud.
4. The negative charge pushed to the spikes passes through the copper rod and is safely diverted to the earth.
5. The lightning arrester does not stop the lightning; rather it diverts the lightning to the ground safely.

Question 22.
Explain in detail the construction and working of a Van-de-Graaff generator.
Answer:
Principle:
Electrostatic induction and action at points.

Construction:

1. Hollow metallic sphere A is mounted on an insulating pillar.
2. Pulley B is mounted at the center of the sphere.
3. Pulley C is mounted near the bottom.
4. A silk belt moves over the pulleys.
5. Pulley C is driven continuously by an electric motor.
6. D and E are the comb-shaped conductors mounted near the pulleys.
   

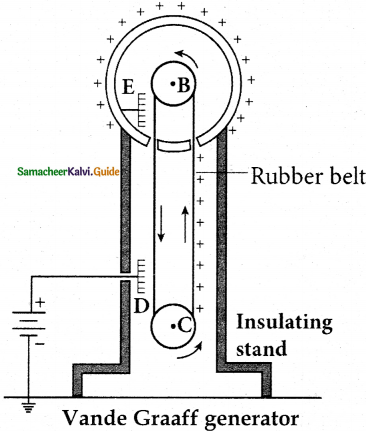
Working:

1. 1. 10⁴ V is given to comb D.
   2. Near the comb, D air gets ionized due to the action of points.
   3. Negative charges move towards the needle and
   4. Positive charges stick to the belt, moves up, and reach the comb E. Due to the electrostatic induction.
   5. Comb E gets a negative charge and the sphere gets a positive charge.
   6. Comb E ionize the air.
   7. Hence descending belt will be. left uncharged.
   8. The machine transfers the positive charge to the sphere.
   9. Leakage of charges can be reduced by enclosing it in a gas-filled steel chamber at very high pressure.
   10. It produces a large potential 10⁷v.

Uses:
To accelerate positive ions (protons, deuteron) for the purpose of nuclear disintegration.

IV.Exercises:

Question 1.
When two objects are rubbed with each other, approximately a charge of 50 nC can be produced in each object. Calculate the number of electrons that must be transferred to produce this charge.
Answer:

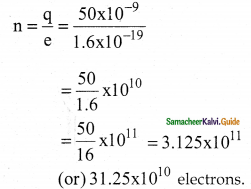
Question 2.
The total number of electrons in the human body is typically in the order of 10²⁸. Suppose, due to some reason, you and your friend lost 1% of this number of electrons. Calculate the electrostatic force between you and your friend separated at a distance of lm. Compare this with your weight. Assume the mass of each person is 60kg and use point charge approximation.
Answer:

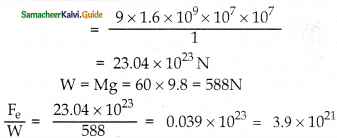
Question 3.
Five identical charges Q are placed equidistant on a semicircle as shown in the figure. Another point charge q is kept at the center of the circle of radius R. Calculate the electrostatic force experienced by the charge q.

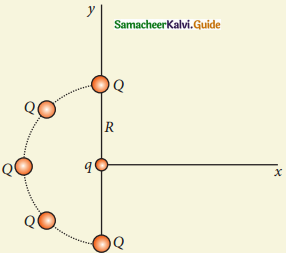
Answer:


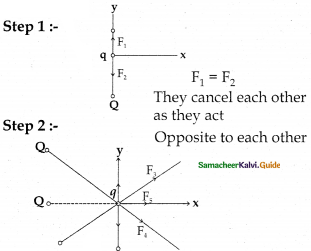
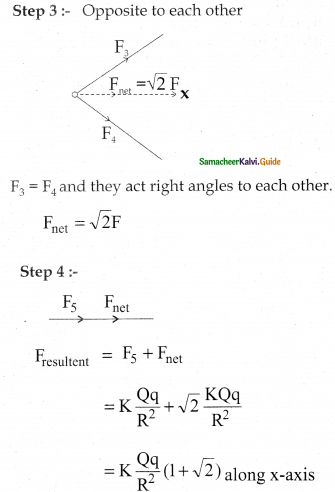
\(\mathrm{F}_{\text {resultent }}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{\mathrm{Qq}}{\mathrm{R}^{2}}(1+\sqrt{2}) \hat{\mathrm{i}}\)

Question 4.
Suppose a charge +q on Earth’s surface and another +q charge is placed on the surface of the Moon.
(a) Calculate the value of q required to balance the gravitational attraction between Earth and the Moon
(b) Suppose the distance between the Moon and Earth is halved, would the charge q change?
(Take m_E = 5.9 × 10²⁴ kg, M_m = 7.9 × 10²² (kg)
Answer:

Question 5.
Draw the free body diagram for the following charges as shown in figure (a), (b) and (c).
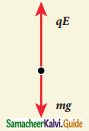
a)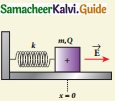
Answer:

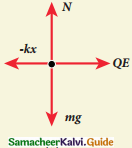
b)
Answer:

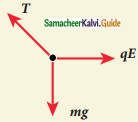
c)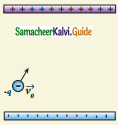
Answer:

Question 6.
Consider an electron travelling with a speed y0 and entering into a uniform electric field which is perpendicular to as shown in the Figure. Ignoring gravity, obtain the electron’s acceleration, velocity, and position as functions of time.

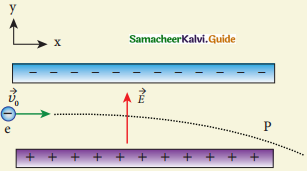
Answer:

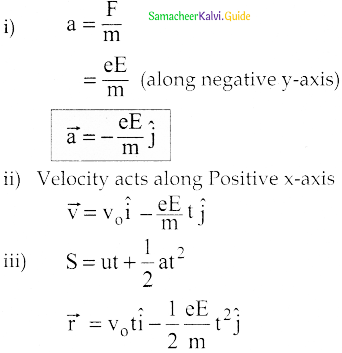
Question 7.
A closed triangular box is kept in an electric field of magnitude E = 2 × 10^-3 NC^-1 as shown in the figure.

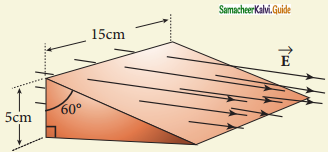
Calculate the electric flux through the
(a) vertical rectangular surface
Answer:

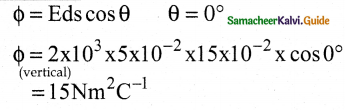
(b) slanted surface
Answer:

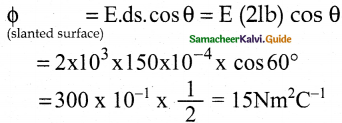
c) entire surface.
Answer:

Question 8.
The electrostatic potential is given as a function of x in figure (a) and (b). Calculate the corresponding electric fields in regions A, B. and D. Plot the electric field as a function of x for figure (b)

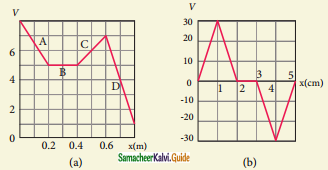
Answer:
Figure a:
\(\overrightarrow{\mathrm{E}}=-\frac{\mathrm{d} \mathrm{v}}{\mathrm{d} \mathrm{x}} \hat{\mathrm{i}}\)
From 0 to 0.2 m,

Figure b:

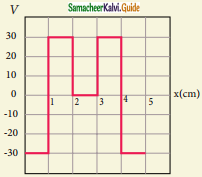
Question 9.
A spark plug in a bike or a car is used to ignite the air-fuel mixture in the engine. It consists of two electrodes separated by a gap of around 0.6 mm gap as shown in the figure.

To create the spark, an electric field of magnitude 3 × 10⁶ Vm^-1 is required.
Question (a)
What potential difference must be applied to produce the spark?
Answer:
V = E × d
= 3 × 10⁶ × 0.6 × 10^-3
= 1800 V

Question (b)
If the gap is increased, does the potential difference increase, decrease, or remains the same?
Answer:
If the distance between the plate increased, then its capacitance will decrease which gives rise to an increase in potential

Question (c)
Find the potential difference if the gap is 1 mm.
Answer:
V = E × d
= 3 × 10⁶ × 1 × 10^-3
= 3000 V

Question 10.
A point charge of +10 μC is placed at a distance of 20 cm from another identical point charge of +10 μC. A point charge of -2 μC is moved from point a to b as shown in the figure. Calculate the change in potential energy of the system? Interpret your result.

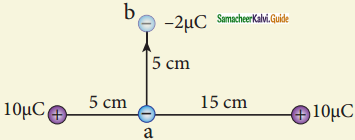
Answer:

Question 11.
Calculate the resultant capacitances for each of the following combinations of capacitors.

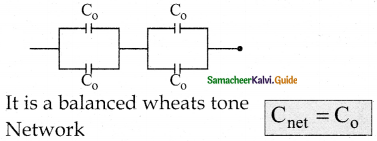
Question a.

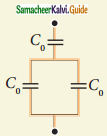
Answer:

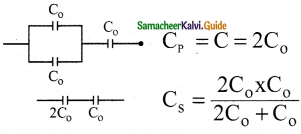
Question b.

Answer:

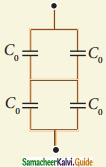
Question c.

Answer:

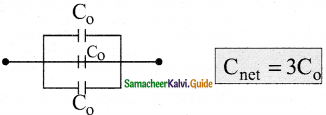
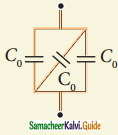
Question d.

Answer:

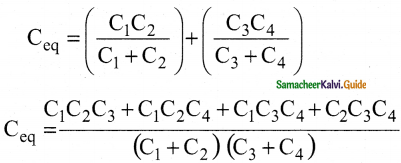
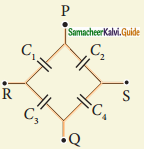
Question e.

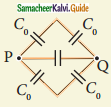
Answer:

Question 12.
An electron and a proton are allowed to fall through the separation between the plates of a parallel plate capacitor of voltage 5 V and separation distance h = 1 mm as shown in the figure. (Take m_p =1.6 × 10^-27 kg, m_e =9.1 × 10^-31 kg and g= 10ms^-2)

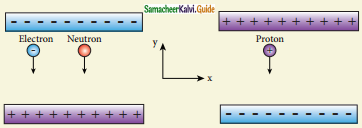
Question (a)
Calculate the time of flight for both electron and proton
Answer:
E = \(\begin{array}{l}
\mathrm{V} \\
\hline \mathrm{d}
\end{array}[latex]
= [latex]\frac{5}{10^{-3}}\)
= 5 × 10³ Vm^-1

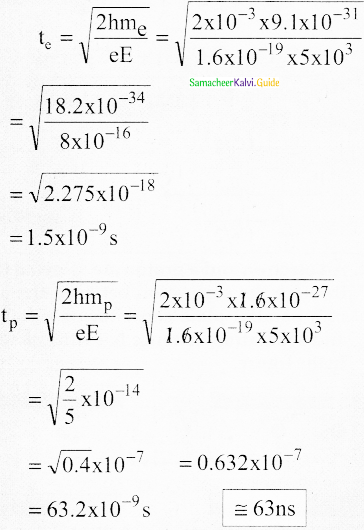
Question (b)
Suppose if a neutron is allowed to fall, what is the time of flight?
Answer:

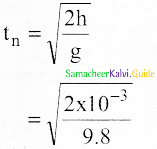
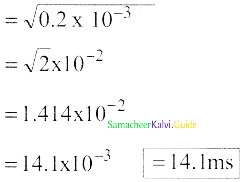
Question (c)
Among the three, which one will reach the bottom first?
Answer:
Hence electron will reach the bottom first.

Question 13.
During a thunderstorm, the movement of water molecules within the clouds creates friction, partially causing the bottom part of the clouds to become negatively charged. This implies that the bottom of the cloud and the ground act as a parallel plate capacitor. If the electric field between the cloud and ground exceeds the dielectric breakdown of the air (3 × 10⁶ Vm^-1), lightning will occur.

Question (a)
If the bottom part of the cloud is 1000m above the ground, determine the electric potential difference that exists between the cloud and ground.
Answer:
\(\mathrm{E}=\frac{\mathrm{d} \mathrm{v}}{\mathrm{d} \mathrm{x}}\)
V = E.x
= 3 ×10⁶ ×10³
= 3 × 10⁹ V

Question (b)
In a typical lightning phenomenon, around 25 C of electrons are transferred from cloud to ground. How much electrostatic potential energy is transferred to the ground?
Answer:

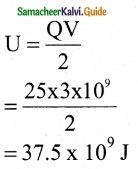
Question 14.
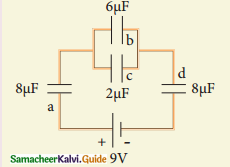
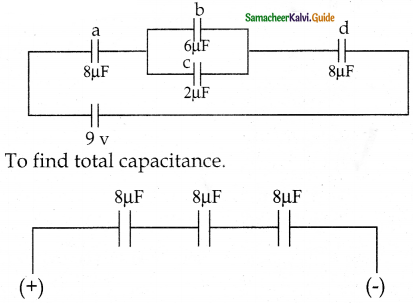
For the given capacitor configuration
a) Find the charges on each capacitor
b) potential difference across them
c) energy stored in each capacitor.

Answer:

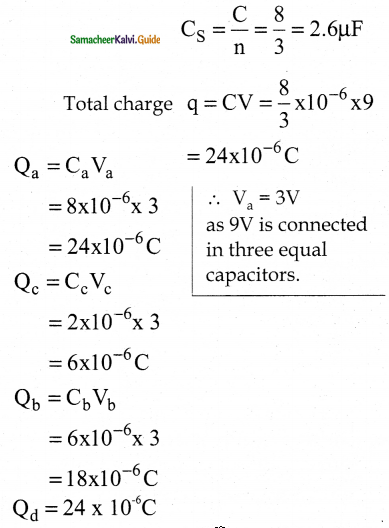
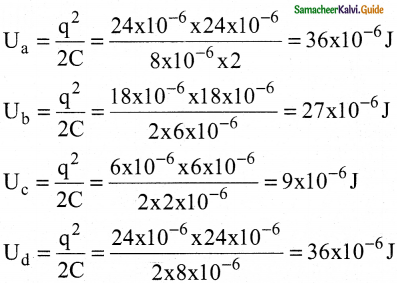
Question 15.
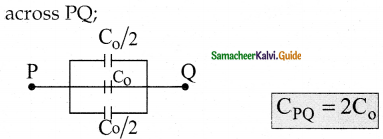
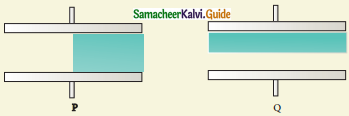
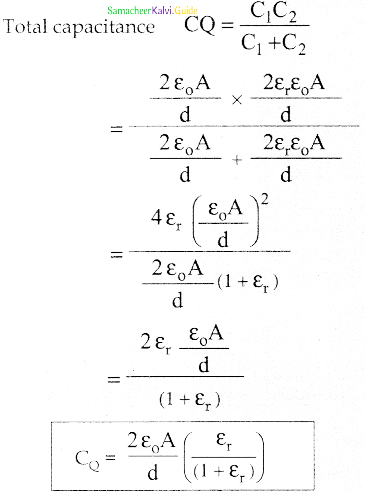
Capacitors P and Q have identical cross-sectional areas A and separation d. The space between the capacitors is filled with a dielectric of dielectric constant Er as shown in the figure. Calculate the capacitance of capacitors P and Q.

Answer:
1. The arrangement can be supposed to be a parallel combination of two capacitors each with plate area A/2 and separation. d. Total capacitance C_p = C_air + C_dielectric

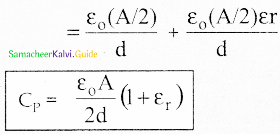
2. The arrangement can be supposed to be a series combination of two capacitors, each with plate area A and separation d/2.

Part – II:

12th Physics Guide Electrostatics Additional Important Questions and Answers

I. Matching Type Questions:

Question 1.
Match Column I and Column II.

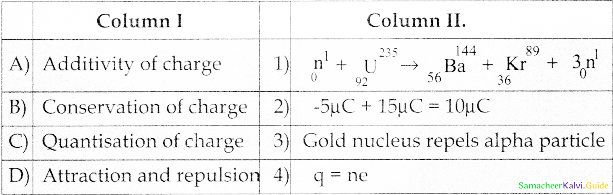
Answer:
(A) → (2)
(B) → (1)
(C) → (4)
(D) → (3)

Question 2.
Match Column I and Column II.

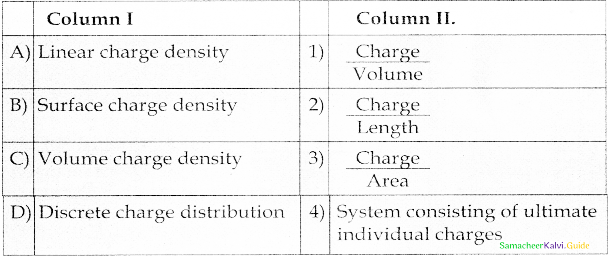
Answer:
(A) → (2)
(B) → (3)
(C) → (1)
(D) → (4)

Question 3.
Match the entries of Column I and Column II.

Column I	Column II
A) Inside a conductor placed in an external electric field	1. Potential energy = 0
B) At the centre of a dipole	2. Electric field = 0
C) Dipole in stable equilibrium	3. Electric potential = 0
D) Electric dipole perpendicular to the uniform electric field	4. Torque = 0

Answer:
(A) → (2)
(B) → (4)
(C) → (3)
(D) → (1)

Question 4.
When a dielectric slab is inserted between the plates of one of the two identical capacitors shown in the figure then match the following:

Column I	Column II
A) Charge on A	1. Increases
B) PotentIa1difference across A	2. Decreases
C) Potential difference across B	3. Remains constant
D) Charge on B	4. Cannot say

Answer:
(A) → (1)
(B) → (1)
(C) → (2)
(D) → (2)

II. Assertion – Reason Type Questions:

a) Assertion is correct, reason is correct; reason is a correct explanation for assertion.
b) Assertion is correct, reason is correct; reason is not a correct explanation for assertion.
c) Assertion is correct, reason is incorrect
d) Assertion is incorrect, reason is correct.

Question 1.
Assertion:
Four-point charges q_1, q₂, q_3, and q₄ are as shown in figure. The flux over the shown Gaussian surface depends only on charges q₁ and q₂.
Reason:
Electric field at all points on Gaussian surface depends only on charges q₁ and q₂,

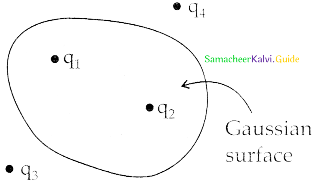
Answer:
(d) Assertion is incorrect, reason is correct.

Question 2.
Assertion:
On disturbing an electric dipole in stable equilibrium in an electric field, it returns back to its stable equilibrium orientation.
Reason :
A restoring torque acts on the dipole on being disturbed from its stable equilibrium.
Answer:
(a) Assertion is correct, reason is correct; reason is a correct explanation for the assertion.

Question 3.
Assertion:
Work done in moving a charge between any two points in an electric field is independent of the path followed by the charge, between these points.
Reason :
Electrostatic force is a non-conservative force.
Answer:
(c) Assertion is correct, reason is incorrect

Question 4.
Assertion:
Dielectric polarisation means the formation of positive and negative charges inside the dielectric.
Reason:
Free electrons are formed in this process.
Answer:
(c) Assertion is correct, reason is incorrect

III. Statement Type Questions:

Question 1.
Which of the following about potential difference between any two points is true?
I. It depends only on the initial and final position.
II. It is the work done per unit positive charge in moving from one point to other.
III. It is more for a positive charge of two units as compared to a positive charge of one
Answer:
I and II

Question 2.
Select the correct statements from the following.
I. The electric field due to a charge outside the Gaussian surface contributes zero net flux through the surface.
II. Total flux linked with a closed body, not enclosing any charge will be zero.
III. Total electric flux, if a dipole is enclosed by a surface is zero.
Answer:
I, II, and III

Question 3.
An electric dipole of moment \(\overrightarrow{\mathrm{P}}\) is placed in a uniform electric field \(\overrightarrow{\mathrm{E}}\). Then
I. the torque on the dipole is \(\overrightarrow{\mathrm{P}}\) x \(\overrightarrow{\mathrm{E}}\).
II. the potential energy of the system is \(\overrightarrow{\mathrm{P}}\) x \(\overrightarrow{\mathrm{E}}\).
III. the resultant force on the dipole is zero.
Which of the above statements is/are correct.
Answer:
I and III

Question 4.
Select the incorrect statements from the following.
I. Polar molecules have permanent electric dipole moment.
II. CO₂ molecule is a polar molecule
III. H₂O is a non-polar molecules.
Answer:
II and III

IV. Choose the incorrect statement:

Question 1.
Which of the following statements is incorrect?
I. The charge q on a body is always given by q=ne, where n is any integer positive or negative.
II. By convention, the charge on an electron is taken to be negative charge.
III. The fact that electric charge is always an integral multiple of e is termed as quantisation of charge.
IV. The quantisation of charge was experimently demonstrated by Newton in 1912.
(a) only I
(b) only II
(c) only lV
(d) only III
Answer:
(c) only IV

Question 2.
The energy stored in a parallel plate capacitor is given by \(\mathrm{V}_{\mathrm{E}}=\frac{\mathrm{Q}^{2}}{2 \mathrm{C}}\). Now which of the following statements is not true?
I. The work done in charging a capacitor is stored in the form of electrostatic potential energy \(\mathrm{V}_{\mathrm{E}}=\frac{\mathrm{Q}^{2}}{2 \mathrm{C}}\)
II. The net charge on the capacitor is Q.
III. The magnitude of the net charge on one plate of a capacitor is Q.
(a) I only
(b) II only
(c) I and II
d) I, II and III
Answer:
(b) II only

Question 3.
Which of the following is not true ?
I. For a point charge, electrostatic potential varies as 1/r .
II. For a dipole, the potential depends on the magnitude of position vector, and dipole moment vector.
III. The electric potential varies as is at large distance.
IV. For a point charge, the electrostatic field varies as \( \frac{1}{\mathrm{r}^{2}}\).
(a) I only
(b) II only
(c) III only
(d) I, II and III
Answer:
(c) III only

V. Diagram – Type Question:

Question 1.
The figure shows a charge +q at point P held in equilibrium in air with the help of four + q charges situated at the vertices of a square. The net electrostatic force on q is given by

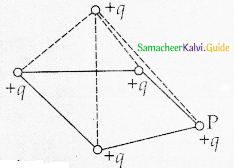
(a) Gauss’s law
(b) Coulomb’s law
(c) Principle of superposition
(d) net electric flux out the position of +q.
Answer:
(c) Principle of superposition
Solution:
The weight mg of the charge hole in air is in equilibrium with the net electrostatic force exerted by the four charges situated at the corners. The net electrostatic force is given by the charges at the corners. This is the principle of superposition.

Question 2.
Which of the following graphs shows the correct variation of force when the distance r between two charges varies?


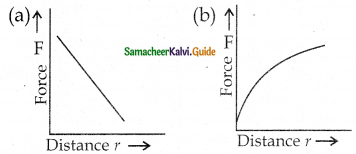
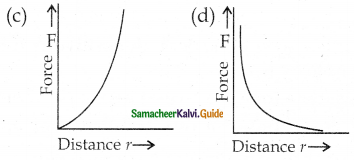
Answer:

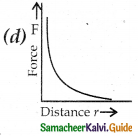
Solution:
From Coulombs’ law \(\mathrm{F}=\frac{\mathrm{Kq}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}\) i.e., \(\mathrm{F} \propto \frac{1}{\mathrm{r}^{2}}\) which is correctly shown by graph (d).

Question 3.
Figure shows some of the electric field lines corresponding to an electric field. The figure suggests that

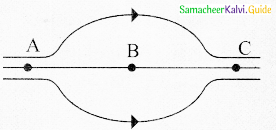
(a) E_A > E_B > E_C
(b)E_A = E_B = E_C
(c) E_A > E_C > E_B
(d) E_A > E_C > E_B
Answer:
(c) ) E_A > E_C > E_B

VI. Choose the odd man out:

Question 1.
(a) lightning arrestor
(b) Van-de-Graf generator
(c) Photocopying
(d) AC generator
Answer:
(d) AC generator

Question 2.
(a) Gold
(b) Silver
(c) electric potential
(c) Aluminium
(d) ebonite
Answer:
(d) ebonite

Question 3.
(a) Farad
(b) \(\frac{J}{C} m^{-1}\)
(c) Vm^-1
(d) NC^-1
Answer:
(a) Farad

Question 4.
(a) electric field
(b) electric force
(c) electric potential
(d) electric dipole moment
Answer:
(c) electric potential

VII. Choose The Incorrect Pair:
Question 1.

Column I	Column II
A) Electric dipole moment	1. Point towards positive charge
B) Electric field	2. Scalar product
C) Electric flux	3. Vector product
D) Torque	4. Nm

Answer:
C) Electric flux – Vector product

Question 2.

Column I	Column II
A) Coulomb’s law	1. Force is directly proportional to the square of the distance
B) Gauss’s law	2.Total electric flux through a closed surface
C) Principle of superposition	3. Vector sum of forces
D) Quantisation of charge	4. Discrete nature of charge

Answer:
A) Coulomb’s law – Force is directly proportional to square of distance

VIII. Choose the correct pair:

Question 1.

Column I	Column II
A) Electro potential near an isolated point positive charge	1. Negative
B) Electric potential near an isolated negative charge.	2. Infinite
C) Electric potential due to a charge on its own location is not defined	3. Positive
D) Electric potential due to a uniform charged solid non-conducting sphere.	4. Varies inversely of radius

Answer:
D) Electric potential due to a uniform charged solid non-conducting sphere – Varies inversely of radius

Question 2.

Column I	Column II
A) Inside a conductor placed in an external electric field.	1. Electric field = 0
B) At the center of a dipole.	2. Torque = 0
C) Dipole in stable equilibrium	3. Potential energy=0
D) Electric dipole perpendicular to uniform electric field.	4. Electric potentials

Answer:
A) Inside a conductor placed in an external electric field – Electric field = 0

IX. Fill In the blanks:

Question 1.
The charge acquired by 5 ×  10¹⁰ electrons _______.
Answer:
q = ne
q = 5 × 10¹⁰ × l.6 × 10^-19 = 8 × 10^-9 C

Question 2.
The unit of permittivity is…………………
Answer:
C²N^-1m^-2

Question 3.
At sharp points, the charge density is ________.
Answer:
maximum

Question 4.
The charges in an electrostatic field are analogous to ………………… in a gravitational field.
Answer:
mass

X. Choose the best answer:

Question 1.
If electric field in a region is radially outward with magnitude E = Ar, the charge contained in a sphere of radius r centred at the origin is
(a) \(\frac{1}{4 \pi \varepsilon_{o}} A r^{3}\)
(b) \(4 \pi \varepsilon_{\mathrm{o}} \mathrm{Ar}^{3}\)
(c) \(\frac{1}{4 \pi \varepsilon_{0}} \frac{A}{r^{3}}\)
(d) \(\frac{4 \pi \varepsilon_{0}}{\mathrm{r}^{3}}\)
Answer:
b) \(4 \pi \varepsilon_{\mathrm{o}} \mathrm{Ar}^{3}\)
Solution:

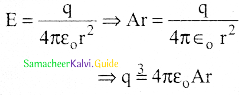
Question 2.
The electric field intensity just sufficient to balance the earth’s gravitational attraction on an electron will be: (given
(a) -5.6 × 10^-11N/C
(b) -4.8 × 10^-15N/C
(c) -1.6 × 10^-19N/C
(d) -3.2 × 10^-19N/C
Answer:
(a) -5.6 × 10^-11N/C
Solution:

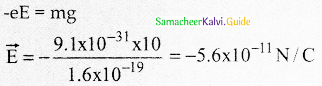
Question 3.
The insulation property of air breaks down when the electric field is 3 × 10⁶ vm^-1 The maximum charge that can be given to a sphere of diameter 5m is approximately
(a) 2 × 10^-2 C
(b) 2 × 10^-3 C
(c) 2 × 10^-4 C
(d) 2 × 10^-5 C
Answer:
(b) 2 × 10^-3 C
Solution:

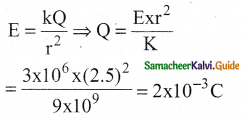
Question 4.
ABC is an equilateral triangle. Charges +q are placed at each corner as shown in fig. The electric intensity at centre 0 will be

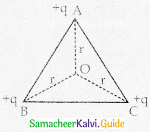
(a) \(\frac{1}{4 \pi \epsilon_{0}} \frac{\mathrm{q}}{\mathrm{r}}\)
(b) \(\frac{1}{4 \pi \epsilon_{0}} \frac{q}{r^{2}}\)
(c) \(\frac{1}{4 \pi \epsilon_{o}} \frac{3 q}{r^{2}}\)
(d) zero
Answer:
(d) zero
Solution:
(Unit positive charge at 0 will be repelled equally by three charges at the three corners of the triangle. By symmetry, the resultant at 0 would be zero.)

Question 5.
A hollow insulated conduction sphere is given a positive charge of 10μC. What will be the electric field at the centre of the sphere if its radius is 2m?
(a) Zero
(b) 5μCm^-2
(c) 20μCm^-2
(d) 8μCm^-2
Answer:
(a) zero
Solution:
(Charge resides on the outer surface of a conducting hollow sphere of radius R. We consider a spherical surface of radius r< R.)

Question 6.
Five balls marked 1, 2, 3, 4, and 5 are suspended by separate threads. The pairs (1, 2) (2, 4) and (4, 1) show mutual attraction and the pairs (2, 3) and (4, 5) show repulsion. The nature of ball marked as 1 is
a) positive
b) negative
c) neutral
d) can’t determine
Answer:
c) neutral

Question 7.
The resultant capacitance of four plates, each is having an area A, arranged, as shown above, will be (plate separation is d)

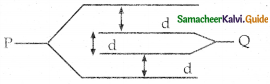
(a) \(\frac{A \varepsilon_{0}}{d}\)
(b) \(\frac{\mathrm{A} \varepsilon_{\mathrm{o}}}{2 \mathrm{~d}}\)
(c) \(\frac{2 \mathrm{~A} \varepsilon_{\mathrm{o}}}{\mathrm{d}}\)
(d) \(\frac{3 A \varepsilon_{o}}{d}\)
Answer:
(c) \(\frac{2 \mathrm{~A} \varepsilon_{\mathrm{o}}}{\mathrm{d}}\)

Question 8.
At infinity, the electrostatic potential is
(a) Infinity
(b) maximum
(c) minimum
(d) zero
Answer:
(d) zero

Question 9.
The electric field at a point on the equatorial line of a dipole and direction of the dipole moment

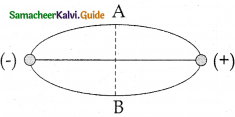
(a) will be parallel
(b) will be in the opposite direction
(c) will be perpendicular
(d) are not related
Answer:
(b) will be in the opposite direction
Solution:
(The direction of the electric field at equatorial point A or B will be in opposite direction, like that of direction of dipole moment.)

Question 10.
Debye is the unit of
(a) electric flux
(b) electric dipole moment
(c) electric potential
(d) electric field intensity
Answer:
(b) electric dipole moment

Question 11.
In the given diagram a point charge +q is placed at the origin 0. Work done in taking another point charge -Q from point A to point B is:

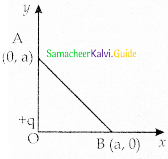
(a) \(\frac{q Q}{4 \pi \epsilon_{0} a^{2}}\left(\frac{a}{\sqrt{2}}\right)\)
(b) zero
(c) \(\left[\frac{-\mathrm{q} \mathrm{Q}}{4 \pi \epsilon_{0}} \frac{1}{\mathrm{a}^{2}}\right] \sqrt{2} \mathrm{a}\)
(d) \(\left[\frac{\mathrm{qQ}}{4 \pi \epsilon_{0}} \frac{1}{\mathrm{a}^{2}}\right] \sqrt{2} \mathrm{a}\)
Answer:
(b) zero

Question 12.
The total electric flux emanating from a closed surface enclosing an α -particle is (e-electronic charge)
(a) \(\frac{2 e}{\varepsilon_{0}}\)
(b) \(\frac{e}{\varepsilon_{0}}\)
(c) \(\mathrm{e} \varepsilon_{\mathrm{o}}\)
(d) \(\frac{\varepsilon_{0} \mathrm{e}}{4}\)
Answer:
(a) \(\frac{2 e}{\varepsilon_{0}}\)
Solution:
(According to Gauss’s law total electric flux \(\frac{1}{\varepsilon_{0}}\) through a closed surface is time the total charge inside that surface.
Electric flux, Φ_E = \(\frac{\mathrm{q}}{\varepsilon_{\mathrm{o}}}\)
Charge on a-particle = 2e)
Φ_E = \(\frac{2 e}{\varepsilon_{o}}\)

Question 13.
A coil of the area of cross-section 0.5 m² with 10 turns is in a plane that is parallel to a uniform electric field of 100 N/C. The flux through the plane is?
(a) 100 V.m
(b) 500 V.m
(c) 20 V.m
(d) zero
Answer:
(b) 500 V.m

Question 14.
0n moving a charge of Q coulomb by χ cm, WJ of work is done, then the potential difference between the point is
(a) \(\frac{\mathrm{W}}{\mathrm{Q}} \mathrm{v}\)
(b) QWV
(c) \(\frac{Q}{W} V\)
(d) \(\frac{Q^{2}}{W} V\)
Answer:
(a) \(\frac{\mathrm{W}}{\mathrm{Q}} \mathrm{v}\)
Solution:
Potential difference between two points in an electric field is.
V_A – V_B = \(\frac{\mathrm{W}}{\mathrm{q}_{\mathrm{o}}}\)

Question 15.
The positive terminal of 12 V battery is connected to the ground. Then the negative terminal will be
(a) – 6 V
(b) +12 V
(c) zero
(d)- 12V
Answer:
(d) – 12V
Solution:
When negative terminal is grounded, the positive terminal of battery is at +12 V. When positive terminal is grounded, the negative terminal will be at -12 V.

Question 16.
The maximum electric field that a dielectric medium can withstand without break-down is called is
(a) permittivity
(b) dielectric constant
(c) electric susceptibility
(d) dielectric strength
Answer:
(d) dielectric strength

Question 17.
The energy required to charge a parallel plate condenser of plate separation d and plate area of cross-section A such that the uniform electric field between the plates is E is
(a) \(\varepsilon_{0} \mathrm{E}^{2} \mathrm{Ad}\)
(b) \(\frac{1}{2} \varepsilon_{0} \mathrm{E}^{2} \mathrm{Ad}\)
(c) \(\frac{1}{2} \varepsilon_{0} \mathrm{E}^{2} / \mathrm{Ad}\)
(d) \(\varepsilon_{0} \mathrm{E}^{2} / \mathrm{Ad}\)
Answer:
(a) \(\varepsilon_{0} \mathrm{E}^{2} \mathrm{Ad}\)
Solution:
(Energy required to charge the capacitor is W = u = QV)
∵ E = V/d

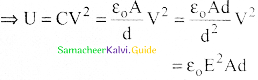
Question 18.
Energy is stored in a capacitor in the form of
(a) electrostatic energy
(b) magnetic energy
(c) light energy
(d) heat energy
Answer:
(a) electrostatic energy

Question 19.
Dimension and unit of Electric flux is
(a) ML²T^-3 A^-2, Nm² C^-1
(b) ML³ T^-3 A^-1, Nm² C^-1
(c) ML² T^-1 A^-2, Nm² C^-1
(d) ML^-4 T^-3 A^-2, Nm² C^-1
Answer:
b) ML³ T^-3 A^-1, Nm² C^-1

Question 20.
An air-core capacitor is charged by a battery. After disconnecting it from the battery, a dielectric slab is fully inserted in between its plates. Now, which of the following quantities remains constant?
(a) Energy
(b) voltage
(c) Electric field
(d) Charge
Answer:
(d) Charge

Question 21.
In a charged capacitor, the energy is stored in
(a) the negative charges
(b) the positive charges
(c) the field between the plates
(d) both (a) and (b)
Answer:
(c) the field between the plates

Question 22.
The potential gradient at which the dielectric of a condenser just gets punctured is called
(a) dielectric constant
(b) dielectric strength
(c) dielectric resistance
(d) dielectric number
Answer:
(b) dielectric strength

Question 23.
The unit of permittivity is
(a) C²N^-1m^-2
(b) Nm²C^-2
(c) Hm^-1
(d) NC^-2m^-2
Answer:
(a) C²N^-1

Question 24.
In the case of a Van de Graaff generator, the breakdown field of air is
(a) 2 × 10⁸ Vm^-1
(b) 3 × 10⁶ Vm^-1
(c) 2 × 10⁸ Vm^-1
(d) 2 × 10⁴ Vm^-1
Answer:
(b) 3 × 10⁶ Vm^-1

Question 25.
Van de Graaff generator is used to
(a) store electrical energy
(b) build up the high voltage of a few million volts
(c) decelerate charged particle-like electrons
(d) both (a) and (b)
Answer:
(b) build up the high voltage of a few million volts

XI. Two mark questions:

Question 1.
What is meant by triboelectric charging?
Answer:
Charging the objects through rubbing is called triboelectric charging.

Question 2.
When does an object is said to be electrically neutral?
Answer:
If the net charge is zero in an object, It is said to be electrically neutral.

Question 3.
State Gauss’s Law?
Answer:
Definition:
Gauss’s law states that if a charge Q is enclosed by an arbitrary closed surface, then the total electric flux OE through the closed surface is Φ_E = \(\oint { \vec { E } } \) .d\(\vec { A } \) = \(\frac {{ q }_{encl}}{{ ε }_{0}}\)

Question 4.
State coulomb’s law.
Answer:
Coulomb’s law states that the force of attraction or repulsion between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.

Question 5.
What is meant by dielectric?
Answer:
A dielectric is a non-conducting material and has no free electrons. The electrons in a dielectric are bound within the atoms. Ebonite, glass, and mica are some examples of dielectrics.

Question 6.
What is meant by the superposition principle?
Answer:
The total force on a given charge is the vector sum of the forces exerted on it due to all other charges. The force on q, due to charges q < ₂, q < ₃ ………… q_n

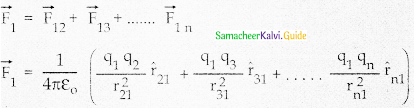
Question 7.
What are polar molecules? Give examples.
Answer:
In polar molecules, the centers of the positive and negative charges are separated even in the absence of an external electric field. They have a permanent dipole moment.
The net dipole moment is zero in the absence of an external electric field. Examples of polar molecules are H₂O, N₂O, HCl, NH₃.

Question 8.
Explain the working of a microwave oven?
Answer:

1. It works on the principle of torque acting on an electric dipole.
2. The food we consume has water molecules which are permanent electric dipoles.
3. Oven produces microwaves that are oscillating electromagnetic fields and produce a torque on the water molecules.
   
4. Due to this torque on each water molecule, the molecules rotate very fast and produce thermal energy.
5. Thus, the heat generated is used to cook the food.

Question 9.
What are permittivity and relative permittivity? How are they related?
Answer:

• Permittivity of a medium = permittivity of free space × relative permittivity, ε = ε₀ ε_r
  Its unit is C² N^-1 m^-2
• Relative permitivity = \(\frac{\text { permitivity of a medium }}{\text { permitivity of vacuum }}=\varepsilon_{\mathrm{r}}=\frac{\varepsilon}{\varepsilon_{\mathrm{o}}}\)
• It has no unit.

Question 8.
What is a capacitor?
Answer:
The capacitor is a device used to store electric charge and electrical energy. Capacitors are widely used in many electronic circuits and have applications in many areas of science and technology.

Question 11.
State Gauss law?
Answer:
Gauss law states that the total flux of the electric field E over any closed surface is equal to l/£0 times of the net charge enclosed by the surface,
\(\phi_{\mathrm{E}}=\frac{\mathrm{q}}{\varepsilon_{\mathrm{o}}}\)

Question 12.
What is meant by electrostatic shielding?
Answer:

• It is the process of isolating a certain region of space from external field.
• It is based on the fact that electric field inside a conductor is zero.

Question 13.
What is meant by electrostatic Induction?
Answer:

• The phenomenon of producing induced charges without any contact with another charge is known as electrostatic induction.
• Electrostatic induction is used in electrostatic machines like Van de Graaff generators and capacitors.

Question 14.
Define farad.
Answer:
A conductor has a capacitance of one farad; if a charge of 1 coulomb given to it, rises its potential by 1 volt.

Question 15.
What are dielectrics? Give examples.
Answer:
A dielectric is an insulating material in which all the electrons are tightly bound to the nucleus of the atom. There are no free electrons to carry current.
E.g:- Ebonite, mica, and oil.

Question 16.
Can two equipotential surfaces intersect? Give reason.
Answer:
Since the electric field is normal to the equipotential surface and also the potential difference between any two points on the surface is nullified, the intersection is not possible.

Question 17.
Distinguish between polar and non-polar molecule?
Answer:

Polar molecules	Non-polar molecules
1. A polar molecule is one in which the centre of gravity of the positive charges is separated from the centre of gravity of the negative charges by a finite distance.	1. Non-polar molecules are one in which the centre of gravity of the positive charges coincides with the centre of gravity of the negative charges.
2. They have a permanent dipole moment Examples: N2O, H2O, HCL, NH3	2. They don’t have a permanent dipole moment Examples: O2, N2, H2

Question 18.
What is meant by dielectric breakdown?
Answer:
When the external electric field applied to a dielectric is very large, it tears the atoms apart so that the bound charges become free charges. Then the dielectric starts to conduct electricity. This is called dielectric breakdown.

Question 19.
The electric field outside a conductor is perpendicular to its surface. Justify.
Answer:

• The electric field has components parallel to the surface of the conductor.
• The free electrons in the conductor would experience acceleration.
• The conductor is not in equilibrium. At electrostatic equilibrium, the electric field must be perpendicular to its surface.

Question 20.
What is called ‘fringing field’ is a capacitor? when does it ignore?
Answer:
For finite-sized plates, the electric field is not strictly uniform between the plates. At both edges, the electric field is bent outward. Under the condition (d²<< A), this effect can be ignored.

Question 21.
How does a capacitor is used in a Computer keyboard?
Answer:
When the key is pressed, the separation between the plates decreases leading to an increase in the capacitance. This is turn triggers the electronic circuits in the computer to identify which key is pressed.

Question 22.
What will happen to the charge, voltage, electric field, the capacitance of a dielectric placed capacitor when it is connected with a battery and then disconnected?
Answer:

Dielectric is inserted	Charge (Q)	Voltage (V)	Electric field (E)	Capacitance (C)	Energy (U)
1. When the battery is disconnected	Constant	Decreases	Decreases	Increases	Decreases
2. When the battery is connected	Increases	Constant	Constant	Increases	Increases

Question 23.
Calculate the number of electrons in one Coulomb of negative charge.
Solution:
According to the quantisation of charge q = ne
Here q = 1C. So the number of electrons in 1 coulomb of charge is
\(\mathrm{N}=\frac{q}{e}=\frac{1 \mathrm{C}}{1.6 \mathrm{X} 10^{-19}}=6.25 \times 10^{18} \text { electrons }\)

Question 24.
Define electric potential energy of two point charges?
Answer:
It is equal to work done to assemble the charges or work done in bringing each charge or work done in bringing a charge from an infinite distance.

Question 25.
Why is it safer to be inside a car than standing under a tree during lightning?
Answer:

• The metal body of the car provides electrostatic shielding.
• The electric field inside the car is zero.
• During lightning, the electric discharge passes through the body of the car. So during lightning, it is safer to sit inside a car than on open ground or under a tree.

Question 26.
Define the electric potential energy of an electric dipole placed in an electric field.
Answer:
Electric potential energy of an electric dipole in an electrostatic field is the work done in rotating the dipole to the desired position in the field.

Question 27.
What happens if a polar molecule is placed in an electric field?
Answer:

1. When a polar molecule is placed in an electric field, the dipoles orient themselves in the direction of the electric field. Hence a net dipole moment is produced.
2. The alignment of dipole moments in the direction of the applied electric field is called polarisation of electric polarisation.
3. The magnitude of the induced dipole moment p is directly proportional to the electric field E. The dipole moment, p = αE when α is called molecular polarisability.

Question 28.
Define volt.
Answer:

1. The unit of potential difference is volt.
2. The potential difference between the two points is I volt if 1 joule of work is done in moving 1 coulomb of charge from one point to another against the electric force.

Question 29.
What does an electric dipole experience when kept in a uniform electric field and non-uniform electric field?
Answer:
Uniform electric field:  When a dipole is kept in a uniform electric field at an angle θ, the net force is zero. It experiences a torque \(\vec{\tau}=\overrightarrow{\mathrm{p}} \times \overrightarrow{\mathrm{E}} \quad \tau=p \mathrm{E} \sin \theta\)

Non-uniform electric field: If the dipole is placed in a non-uniform electric field at an angle θ in addition to torque, it also experiences a force.

Question 30.
What is the Effective Capacitance of capacitors connected in series?
Answer:
When a number of capacitors are connected in series, the reciprocal of the effective capacitance is equal to the sum of reciprocal of the capacitances of the individual capacitors.

\(\frac{1}{\mathrm{C}_{\mathrm{s}}}=\frac{1}{\mathrm{C}_{1}}+\frac{1}{\mathrm{C}_{2}}+\ldots \cdot \frac{1}{\mathrm{Cn}}\)

Question 31.
What is the effective capacitance of capacitors connected in parallel?
Answer:
The effective capacitance of the capacitors connected in parallel is equal to the sum of the capacitances of the individual capacitors.
C_p = C₁ + C₂ + ……….. + C_n

Question 32.
What are conductors and insulators? Give examples.
Answer:

1. Bodies which allow the charges to pass through are called conductors.
   e.g. Metals, human body, Earth, etc.
2. Bodies that do not allow the charge to pass through are called insulators.
   (e.g) Glass, mica, ebonite, plastic, etc.

Question 33.
What is meant by point charge?
Answer:
Any charge which occupies a space with dimensions less than its distance away from an observation point considered a point charge.

Question 34.
What is a capacitor?
Answer:
A capacitor is a device used to store electric charge and electrical energy.

Question 35.
Why does a balloon after rubbing stick to a wall?
Answer:
It is due to the polarisation of the wall due to the electric field due to a balloon.

Question 36.
How does the lightning conductor prevent the lightning stroke from the damage of the building?
Answer:

1. When a negatively charged cloud passes over the building, a positive charge will be induced on the pointed conductor.
2. The positively charged sharp points will ionize the air in the vicinity.
3. This will partly neutralise the negative charge of the cloud, thereby lowering the potential of the cloud.
4. The negative charges that are attracted to the conductor travel down to the earth. Thereby preventing the lightning stroke from the damage of the building.

Question 37.
Define the physical quantity whose unit is Vm, and state whether it is scalar or Vector.
Answer:

1. Electric flux has the unit Vm.
2. The number of electric field lines passing through a given area.
3. q = EA cosθ
4. It is a scalar quantity.
5. The other unit is Nm²c^-1.

XII. Three Mark Questions:

Question 1.
Give some important inference, over the expression of the electric field due to an electric dipole on its axial line and equational line.
Answer:
Important inferences
i) The magnitude of the electric field at points on the dipole axis is twice the magnitude of the electric field at points on the equatorial plane. The direction of the electric field at points on the dipole axis is directed along the direction of dipole moment vector \(\overrightarrow{\mathrm{p}}\) but at points on the equatorial plane it is directed opposite to the dipole moment vector, that is along \(\overrightarrow{\mathrm{p}}{-}\).

ii) At very large distances, the electric field due to a dipole varies as \(\frac{1}{\mathrm{r}^{3}}\) electric field due to a dipole at very large distances goes to zero faster than the electric field due to a point charge.

iii) The distance 2a approaches zero and q approaches infinity such that the product 2aq = p is finite, then the dipole is called a point dipole.

Question 2.
Mention some important points on an expression of electric potential due to point charge.
Answer:
Important points :
i) If the source charge q is positive, V > 0. If q is negative, then V is negative and equal to
\(\mathrm{V}=-\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \frac{\mathrm{q}}{\mathrm{r}}\)
ii) The potential due to positive charge decreases as the distance increases, but for a negative charge the potential increases as the distance is increased. At infinity (r = 0) electrostatic potential is zero (V=0).
iii) The electric potential at a point P due to a collection of charges q₁, q₂, q₃,……..q_n is equal to sum of the electric potentials due to individual charges.

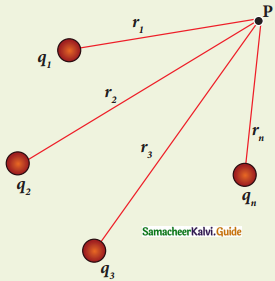
Question 3.
Mention some important points over the derivation of electric potential due to an electric dipole.
Answer:
Important points:
i) The potential due to an electric dipole falls as \(\frac{1}{r^{2}}\) and the potential due to a single point
charge falls as \(\frac{1}{\mathrm{r}}\). Thus the potential due to the dipole falls faster than that due to a monopole. As the distance increases from electric dipole, the effects of positive and negative charges nullify each other.

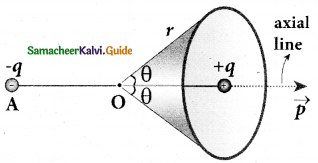
ii) The potential due to a point charge is spherically symmetric since it depends only on the distance r. But the potential due to a dipole is not spherically symmetric because the potential depends on the angle between \(\overrightarrow{\mathrm{p}}\) and position vector \(\overrightarrow{\mathrm{r}}\) of the point.

iii) However the dipole potential is axially symmetric. If the position vector \(\overrightarrow{\mathrm{r}}\) is rotated about \(\overrightarrow{\mathrm{p}}\) by keeping θ fixed, then all points on the cone at the same distance r will have the same potential

Question 4.
Small mercury drops of the same size are charged to the same potential V. If n such drops coalesce to form a single large drop, then calculate its potential.
Solution:
Let r be the radius of a small drop and R that of the large drop. Then, since the volume remains conserved,
\(\frac { 1 }{ 2 }\) πR² = \(\frac { 4 }{ 3 }\) πR³n
⇒ R³ = r³n
R = r³(n)^1/3
Further, since the total charge remains conserved, we have, using Q = CV
C_large V = n C_small v
Where V is the potential of the large drop.
4πε₀ RV = n (4πε₀r)v
V = \(\frac { nrv }{ R }\) = \(\frac { nrv }{{ r(n) }^{1/3}}\)
V = vn^2/3

Question 5.
Derive an expression for electric flux in a non-uniform electric field and an arbitrarily shaped area.
Answer:
1. Suppose the electric field is not uniform and the area is not flat, then the entire area is divided into n small area segments such that each area element is almost flat and the electric field through each area element is considered to be uniform.

2. The electric flux for the entire area A is approximately written as
\(\begin{array}{l}
\Delta \overrightarrow{\mathrm{A}}_{1}, \Delta \overrightarrow{\mathrm{A}}_{2}, \Delta \overrightarrow{\mathrm{A}}_{3} \ldots \ldots \Delta \overrightarrow{\mathrm{A}}_{\mathrm{n}} \\
\Phi_{\mathrm{E}}=\overrightarrow{\mathrm{E}}_{1} \cdot \Delta \overrightarrow{\mathrm{A}_{1}}+\overrightarrow{\mathrm{E}}_{2} \cdot \Delta \overrightarrow{\mathrm{A}}_{2}+\overrightarrow{\mathrm{E}}_{3} \cdot \Delta \overrightarrow{\mathrm{A}}_{3} \ldots . \overrightarrow{\mathrm{E}}_{\mathrm{n}} \cdot \Delta \overrightarrow{\mathrm{A}_{\mathrm{n}}} \\
=\sum_{\mathrm{i}=1}^{\mathrm{n}} \overrightarrow{\mathrm{E}}_{\mathrm{i}} \cdot \Delta \overrightarrow{\mathrm{A}_{\mathrm{i}}}
\end{array}\)

3. By taking the limit \(\Delta \overrightarrow{\mathrm{A}}_{i} \rightarrow 0\) (for all i) the summation in equation becomes integration. The total electric flux for the entire area is given by \(\Phi_{\mathrm{E}}=\int \overrightarrow{\mathrm{E}} \cdot \mathrm{d} \overrightarrow{\mathrm{A}}\)

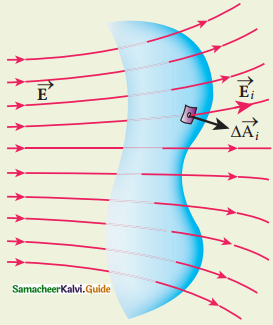
Electric flux for non-uniform electric Field:

1. The electric flux for a given surface depends on both the electric field pattern on the surface area and orientation of the surface with respect to the electric field.

Question 6.
The electric field is zero everywhere inside the conductor. This is true regardless of whether the conductor is solid or hollow. Justify.
Answer:

• This is an experimental fact. Suppose the electric field is not zero inside the metal, then there will be a force on the mobile charge carriers due to this electric field.
•  As a result, there will be a net motion of the mobile charges, which contradicts the conductors being in electrostatic equilibrium. Thus the electric field is zero everywhere inside the conductor.
• We can also understand this fact by applying an external uniform electric field on the conductor.

Question 7.
The electrostatic potential has the same value on the surface and inside the conductor. Justify.
Answer:

• We know that the conductor has no parallel electric component on the surface without doing any work.
• This is possible only if the electrostatic potential is constant at all points on the surface and there is no potential difference between any two points on the surface.
• Since the electric field inside the conductor is zero inside the conductor, the potential is same as the surface of the conductor.
• Thus at electrostatic equilibrium, the conductor is always at equipotential.

Question 8.
Explain Faraday Cage’s experiment? Faraday cage is an instrument to demonstrate the effect of electrostatic shielding.
Answer:

• It is made up of metal bars configured in the instrument.
•  If an artificial lightning bolt is created outside the person inside is not affected.
• This is because the metal bar provides electrostatic shielding.
• The Electric field inside becomes zero.
• The charges flow through the metal bar to the ground with no effect on the person inside.

Question 9.
What do you understand from the expression of capacitance in a parallel plate capacitor?
Answer:
Capacitance is directly proportional to the area of cross-section and is inversely proportional to the distance between the plates.
1. If the area of cross-section of the capacitor plates is increased, more charges can be distributed for the same potential difference. As a result, the capacitance is increased.

2. If the distance d between the two plates is reduced, the potential difference between the plates (V = Ed) decreases with E constant. As a result, the voltage difference between the terminals of the battery increases which in turn leads to an additional flow of charge to the plates from the battery, till the voltage on the capacitor equals to the battery’s terminal voltage. Suppose the distance is increased, the capacitor voltage increases and becomes greater than the battery voltage. Then, the charges flow from capacitor plates to the battery till both voltages become equal.

Question 10.
Mention the applications of capacitors?
Answer:

1. The flash which comes from the digital camera when we take photographs is due to the energy released from the capacitor, called a flash capacitor.
2. During cardiac arrest, a device called heart defibrillator is used to give a sudden surge of a large amount of electrical energy to the patient’s chest to retrieve the normal heart function.
3. Capacitors are used in the ignition system of automobile engines to eliminate sparking.
4. Capacitors are used to reduce power fluctuations in power supplies and to increase the efficiency of power transmission.

XIII – Five mark questions:

Question 1.
Explain the historical background of electric charges?
Answer:

• Two millenniums ago, Greeks noticed that amber after rubbing with animal fur attracted small pieces of leaves and dust.
• The amber possessing this property is said to be charged.
• A glass rod rubbed with a silk cloth, attracts a piece of paper. So glass rod also becomes ‘charged’ when rubbed with a suitable material.
• Consider a charged rubbed rod hanging from a thread.
• Suppose another charged rubber rod is brought near the first rubber rod; the rods repel each other.
• Now if we bring a charged glass rod close to the charged rubber rod, they attract each other.
• At the same time, if a charged glass rod is brought near another charged glass rod both the rods repel each other.

Inferences:
i) The charging of the rubber rod and that of the glass rod are different from one another.
ii) The charged rubber rod repels another charged rubber rod, which implies that Tike charges repel each other’.
iii) The charged amber rod attracts the charged glass rod, implying that the charge in the glass rod is not the same kind of charge present in the rubber. Thus unlike charges attract each other.
Therefore, two kinds of charges exist in the universe. Benjamin Franklin called one type of charge as positive (+) and another type of charge as negative (-). Based on Franklin’s convention, rubber and amber rods are negatively charged while the glass rod is positively charged. If the net charge is zero in the object, it is said to be electrically neutral.

iv) The atom is electrically neutral and is made up of negatively charged electrons, positively charged protons, and neutrons which have zero charges. When an object is rubbed with another object, some amount of charge is transferred from one object to another due to the friction between them, and the object is then said to be ‘electrically charged’. Charging the object through rubbing is called ‘triboelectric charging’.

Question 2.
Derive an expression for electric field due to a system of point charges.
Answer:
Suppose a number of point charges are distributed in space, to find the electric field at some point P due to this collection of point charges, superposition principle is used.

The electric field due to a collection of point charges at an arbitrary point is simply equal to the vector sum of the electric fields created by the individual point charges. This is called the superposition of electric fields.

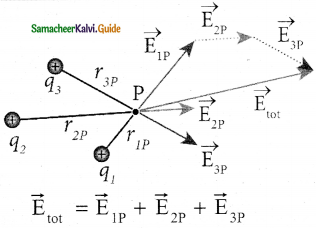
Question 3.
Discuss the electric flux of a uniform electric field?
Answer:
Electric flux for uniform Electric field:

1. Consider a uniform electric field in a region of space. Let us choose an area A normal to the electric field lines.
Φ_E = EA ……….(1)

2. Suppose the same area A is kept parallel to the uniform electric field, then no electric field lines pass through area A. The electric flux for this case is zero.
Φ_E > E = 0 ………..(2)

3. If the area is inclined at an angle e with the field, then the component of the electric field perpendicular to the area alone contributes to the electric flux.

4. The electric field component parallel to the surface area will not contribute to the electric flux. For this case, the electric flux  Φ_E = (E cosθ) A …………..(3)

5. Further, e is also the angle between the electric field and the direction normal to the area, Hence in general, for a uniform electric field, the electric flux is defined as
Φ_E = \(\overrightarrow{\mathrm{E}}\) . \(\overrightarrow{\mathrm{A}}\) = EA cosθ ………………(4)

6. \(\overrightarrow{\mathrm{A}}\) is the area vector \(\overrightarrow{\mathrm{A}}\) = A n̂. Its magnitude is simply the area A and the direction are along the unit vector n̂ perpendicular to the area.

7. Using this definition for flux,
Φ_E = \(\overrightarrow{\mathrm{E}}\) . \(\overrightarrow{\mathrm{A}}\)
equations (2) and (3) can be obtained as special cases.
In Figure (a), θ=0° Φ_E = \(\overrightarrow{\mathrm{E}}\) . \(\overrightarrow{\mathrm{A}}\) = EA
In Figure (b), θ = 90° Φ_E = \(\overrightarrow{\mathrm{E}}\) . \(\overrightarrow{\mathrm{A}}\) = 0
Here \(\overrightarrow{\mathrm{A}}\) = An̂

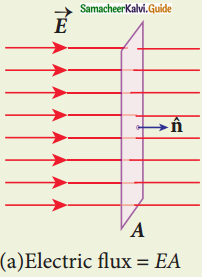
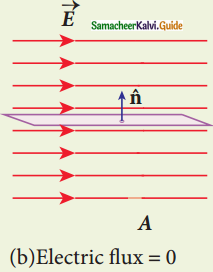
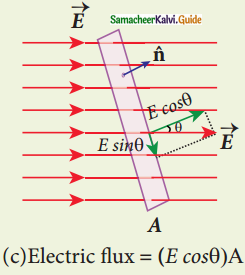
Question 4.
Discuss some salient points about Gauss law?
Answer:
1. The total electric flux through the closed surface depends on the charges enclosed by the surface and the charges present outside the surface will not contribute to the flux and the shape of the closed surface which can be chosen arbitrarily.

2. The total electric flux is independent of the location of the charges inside the closed surface.

3. Chosen imaginary surface is called a Gaussian surface. The shape of the Gaussian surface to be chosen depends on the type of charge configuration and the kind of symmetry existing in that charge configuration.

4. The electric field E is due to charges present inside and outside the Gaussian surface but the charge Qencl denotes the charges which lie only inside the Gaussian surface.

5. The Gaussian surface cannot pass through any discrete charge but it can pass through continuous charge distributions.

6. Gauss law is another form of Coulomb’s law and it is also applicable to the charges in motion. Because of this reason, Gauss law is treated as much more general law than Coulomb’s law.

Question 5.
Derive an expression for electric field due to two parallel charged infinite sheet.
Answer:

1. Consider two infinitely large charged plane sheets with equal and opposite charge densities +σ and -σ which are placed parallel to each other.
2. The electric field between the plate and outside the plates is found using Gauss law.
3. The magnitude of the electric field due to an infinite charged plane sheet is \(\frac{\sigma}{2 \varepsilon}\) and it points perpendicularly outward if σ>0 and points inward if σ<0.
   
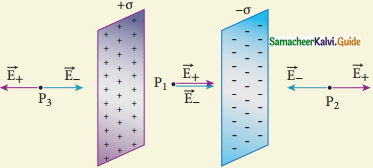
4. At the points P₁ and P₂, the electric field due to both plates are equal in magnitude and opposite in direction. As a result, electric field at a point outside the plate is zero. But inside the plate, electric fields are in the same direction
5. The direction of the electric field inside the plates is directed from positively charged plate to the negatively charged plate and is uniform everywhere inside the plate.
   \(\mathrm{E}_{\text {inside }}=\frac{\sigma}{2 \varepsilon_{0}}+\frac{\sigma}{2 \varepsilon_{0}}=\frac{\sigma}{\varepsilon_{0}}\)

Question 6.
Explain the principle of a capacitor?
Answer:

1. A capacitor is a device used to store electric charge and electric energy.
2. It consists of two conducting objects separated by some distance.
3. A simple capacitor consists of two parallel metal plates separated by a small distance.
4. When a capacitor is connected to a battery of potential difference V, the electrons are transferred from the battery to one plate and the other plate to the battery so that one plate becomes negatively charged with a charge of – Q and the other plate becomes positively charged with + Q.
5. The potential difference between the plates is equivalent to the battery’s terminal voltage. If the battery voltage is increased, the amount of charges stored in the plates also increase.
6. In general, the charge stored in the capacitor is proportional to the potential difference between the plates.
   Q α V, So that Q = CV, where C is the proportionality constant called capacitance.
   
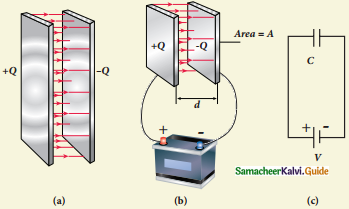
7. The capacitance of a capacitor is defined as the ratio of the magnitude of charge on either of the conductor plates to the potential difference existing between conductors.
8. Unit:- Farad or Coulomb per volt. Farad is a very large unit of capacitance.
9. In Practice, we use micro & picofarad.
10. Total charge stored in the capacitor is zero when we say the capacitor stores charges, it means that amount of charge that can be stores charge, it means that amount of charge that can be stored in any one of the plates.
11. Nowadays it is available in different shapes and types. It is used in various kinds of electronic circuits.

Question 7.
Write the properties of lines of force:
Answer:

1. It starts from positive charge and ends at negative charge .
2. For a positive charge, the electric field lines point radially outward and for a negative charge, electric field lines point radially inward.
3. Tangent drawn at any point gives the direction of the electric field at the point.
4. The electric field lines are denser in a region where the electric field has a larger magnitude and less dense in a region of smaller magnitude.
5. They do not intersect
6. Field lines emanating from the positive charge are proportional to the magnitude of the charge.

XlV. Additional Problems (Two Marks):

Question 1.
An ele1tric dipole of charges 2 × l0^-10C separated by a distance 5 mm, is placed at an angle of 60 to a uniform field of 10 Vm^-1. Find the
i) magnitude and direction of the force acting on each charge and
ii) torque exerted by the field.
Data:
+q = 2 × 10^-10 C
-q = – 2 × 10^-10 C
θ = 60°
E = 10Vm^-1
2d = 5mm = 5 × 10^-3 m
i) Magnitude and directions of the force acts on each charge =?
ii) Torque exerted by the field =?
Solution:

1. Positive charge experience a force in the direction of the field.
2. Negative charge experiences a force opposite to the direction of the field.
   i) To find the force on each charge:
3. Force acts on positive charge: F = qE
   F = 2 × 10^-10 × 10
   F = 2 × l0^-9 × N in the direction of E
   Force acts on negative charge:
   F = qE = 2 × 10^-10 × 10
   F= 2 × l0^-9 N in the direction of E

ii) To find Torque exerted bj the field:

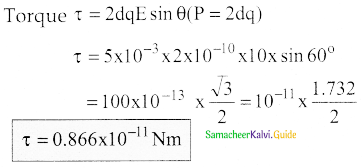
Question 2.
An electric dipole of charges 2 × 10^-6 C, – 2 × 10^-6 C is separated by a distance of 1 cm. Calculate the electric field due to dipole at a points
i) axial line 1 m from its centre and
ii) equatorial line 1 m from its centre.
Answer:


i) Electric field at a point on axial line = 360NC^-1
ii) Electric field at a point on equatorial line = 180NC^-1

Question 3.
Two charges +q and -3q are separated by a distance of lm. At what point in between the charges on its axis is the potential zero?
Answer:
Data :
q₁ = +q; q₂ = -3q; r = 1m
Solution:
Let the potential be zero at point 0 at a d . 1 from +q charge.


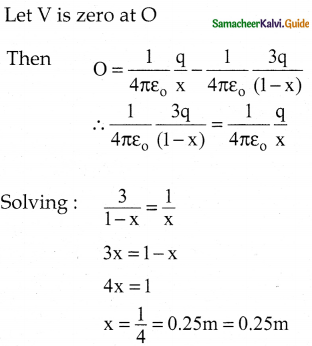
The potential is zero at a distance of 0.25m from the charge +q.

Question 4.
A parallel plate capacitor is maintained at some potential difference. A 3 mm thick slab is introduced between the plates. To maintain the plates at the same potential difference, the distance between the plates is increased by 2.4mm. Find the dielectric constant of the slab.
Data:
t = 3 mm; d’- d = 2.4 mm
V is same;
ε_r = ?
Solution:
Capacitance of air-filled parallel plate capacitor:

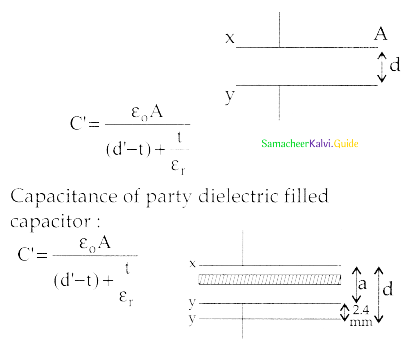
Since the potential are made the same capacitance in the above two cases is also the same.

The dielectric constant of the slab ε_r = 5

Question 5.
Three capacitors each of capacitance 9 pF are connected in series.
i) What is the total capacitance of the combination?
ii) What is the potential difference across each capacitor if the combination is connected to 120 V supply?
Answer:
Data:
C₁ = C₂ = C₃ = 9pF
V = 120V
C_s = ?
V₁, V₂, V₃ =?
To find effective capacitance:
Three capacitors are in series

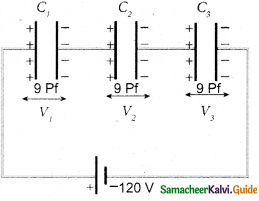
∵ \(\frac{1}{\mathrm{C}_{\mathrm{S}}}=\frac{1}{\mathrm{C}_{1}}+\frac{1}{\mathrm{C}_{2}}+\frac{1}{\mathrm{C}_{3}}=\frac{1}{9}+\frac{1}{9}+\frac{1}{9}\)
C_s = 3pF
C_s = 3 × 10^-12 F

V₁, V₂, V₃ are the potential differences across the three capacitors as shown in the figure.

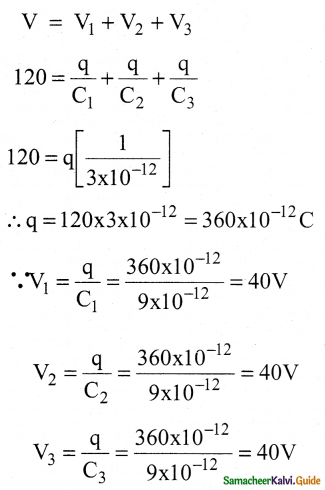
i) C_s = 3 × 10^-12 F
ii) V₁, V₂, V₃ = 40 V

XV. Five Mark Problems:

Question 1.
Four-point charges +q, +q, and -q is to be arranged respectively at the four corners of a square PQRS of side r. Find the work needed to assemble this arrangement.
Solution:

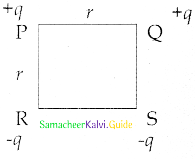
Here PQ = QS = SR= RP = r
\(\mathrm{PS}^{\prime}=\mathrm{RQ}=\mathrm{r} \sqrt{2}\)
W = Potential Energy of the system of four charges.
\(=\frac{(-q)(+q)}{4 \pi \varepsilon_{o} r}+\frac{(+q)(+q)}{4 \pi \varepsilon_{o} r}+\frac{(+q)(-q)}{4 \pi \varepsilon_{o} r}+\frac{(-q)(-q)}{4 \pi \varepsilon_{o} r}\)

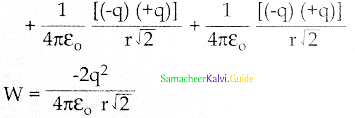
Question 2.
Two small charged spheres repel each other with a force of 2 × 10^-3 N. The charge on one sphere is twice that of the other. When one of the charges is moved 10 cm away from the other, the force is 5 × 10^-4 N. Calculate the charges and the initial distance between them.
Answer:
Data:
F₁= 2 × 10^-3N when distance = r
F₂ = 5 × 10^-4N
when distance (i.e.) r’= (r+ 0. 1)rn
r = r + 10cm
q₁ = ?, q₂ = ?, r =?
Solution:
According to Coulomb’s law
\(\mathrm{F}=\frac{1}{4 \pi \varepsilon_{\mathrm{o}}} \cdot \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}_{2}}\)
Let q₁ = q and q₂ = 2q and distance between the charges be r experience a repulsive force F₁.


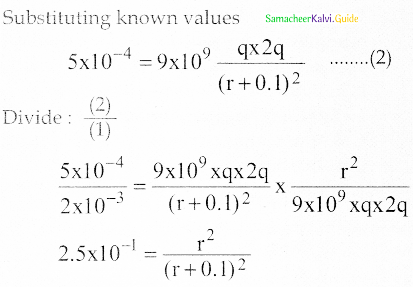
We know,
q₁ = q = 33.3 × 10^-9 C
q₂ = 2q = 2 × 33.3 × 10^-9 C
q₂ =66.6 × 10^-9 C
Initial distance r = 0.1m
Charges:
q₁ = 33.3 × 10^-9 C
q₂ = 66.6 × 10^-9 C

Question 3.
Two capacitors of unknown capacitance are connected in series and parallel. If net capacitances in two combinations are 6µF and 25µF respectively. Find their capacitances.
Answer:
Given:
Cs = 6µF
Cp = 25µF
\(\frac{1}{C_{S}}=\frac{1}{C_{1}}+\frac{1}{C_{2}} \quad \cdots \cdots\)

Question 4.
Three charges + 1 µC, + 3 µC, and – 5 µC are kept at the vertices of an equilateral triangle of sides 60 cm. Find the electrostatic potential energy of the system of charges.
Answer:


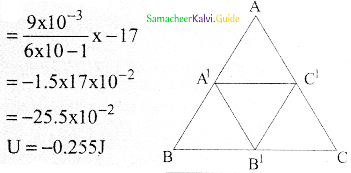
The electrostatic potential energy of the system of charges = – 0.255 J

Question 5.
Calculate the force between electron and proton in a Hydrogen atom.
(e = 1.6 × 10^-9 and r₀ = 0.53Å)
Solution:
The electron and proton attract each other. The force between these two particles is given by

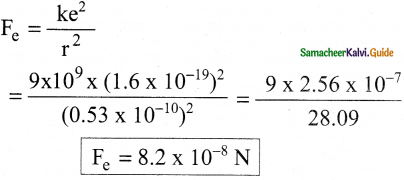
Question 6.
Four point charges are placed at the four corners of a square in two ways (a) and (b) as shown in figure. Will the (i) electric potential and (ii) electric field, at the centre of the square be the same or different in the two configurations, and why?

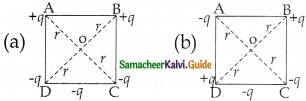
Answer:
a) Electric potential is a scalar quantity. 0pposite charges cancel each other So, in both the configurations electric potential will be zero and the same.
b) Electric field is a vector quantity. It depends on positions of charge.
In the first diagram Electricfield,
\(E=2 \sqrt{2} \frac{\mathrm{kq}}{(\mathrm{r} / \sqrt{2})^{2}}\)
In the second diagram, E= 0
Because opposite charges are placed at the corner.