Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 Applications of Vector Algebra Ex 6.6 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.6
Question 1.
Find a parametric form of vector equation of a plane which is at a distance of 7 units from t the origin having 3, -4, 5 as direction ratios of a normal to it.
Solution:
Let \(\overline { d }\) = \(\hat { i }\) – 4\(\hat { j }\) + 5\(\hat { k }\)
p = 7
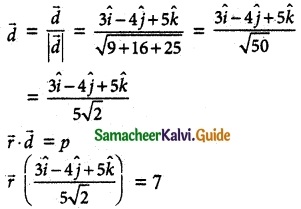
![]()
Question 2.
Find the direction cosines of the normal to the plane 12x + 3y – 4z = 65. Also find the non-parametric form of vector equation of a plane and the length of the perpendicular to the plane from the origin.
Solution:

Length of the ⊥r from the origin = 5 units.
Question 3.
Find the vector and Cartesian equations of the plane passing through the point with position vector 2\(\hat { i }\) + 6\(\hat { j }\) + 3\(\hat { k }\) and normal to the vector \(\hat { i }\) + 3\(\hat { j }\) + 5\(\hat { k }\).
Solution:
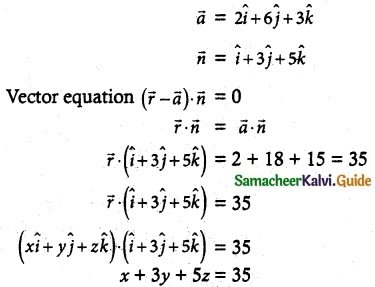
![]()
Question 4.
A plane passes through the point (-1, 1, 2) and the normal to the plane of magnitude 3√3 makes equal acute angles with the co-ordinate axis. Find the equation of the plane.
Solution:
Magnitude = 3√2
Makes equal acute angles with co-ordinate axes l² + m² + n² = 1
cos²A + cos²A + cos²A = 1 ⇒ 3cos²A = 1
⇒ cos²A = \(\frac { 1 }{ 3 }\)
cos A = \(\frac { 1 }{ √3 }\)
\(\overline { n }\) (normal) = ±3√3(\(\frac { \hat{i} }{ √3 }\)+\(\frac { \hat{j} }{ √3 }\)+\(\frac { \hat{k} }{ √3 }\))
= ±(3\(\hat { i }\) + 3\(\hat { j }\) + 3\(\hat { k }\))
Equation of plane passing through (-1, 1, 2) normal (3, 3, 3)
⇒ 3(x + 1) + 3(y – 1) + 3(z – 2) = 0
⇒ 3x + 3 + 3y – 3 + 3z – 6 = 0
⇒ 3x + 3y + 3z – 6 = 0
⇒ x + y + z = 2
Vector equation \(\overline { r }\) (\(\hat { i }\) + \(\hat { j }\) + \(\hat { k }\)) = 2
Question 5.
Find the intercepts cut off by the plane f \(\overline { r }\) (6\(\hat { i }\) + 4\(\hat { j }\) – 3\(\hat { k }\) ) = 12 on the co-ordinate axes
Solution:
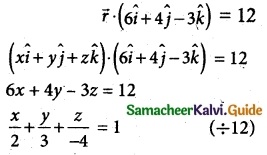
x-intercept = 2, y-intercept = 3, z-intercept = -4
![]()
Question 6.
If a plane meets the co-ordinate axes at A, B, C such that the centroid of the triangle ABC is the point (u, v, w), find the equation of the plane.
Solution:
