Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 Applications of Vector Algebra Ex 6.10 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.10
Choose the most suitable answer from the given four alternatives
Question 1.
If \(\overline { a }\) and \(\overline { b }\) are parallel vectors, then [\(\overline { a }\), \(\overline { c }\), \(\overline { b }\)] is equal to
(a) 2
(b) -1
(c) 1
(d) 0
Solution:
(d) 0
Hint:
Since \(\overline { a }\) and \(\overline { b }\) are parallel ⇒ \(\overline { a }\) = λ\(\overline { b }\)
[ \(\overline { a }, \overline { c }, \overline { b }\)] = [λ\(\overline { b }, \overline { c }, \overline { b }\) ]
= λ[ \(\overline { b }, \overline { c }, \overline { b }\) ]
= λ(0) = 0
![]()
Question 2.
If a vector \(\overline { α }\) lies in the plane of \(\overline { ß }\) and \(\overline { γ }\), then
(a) [ \(\overline { α }, \overline { ß }, \overline { γ }\) ] = 1
(b) [ \(\overline { α }, \overline { ß }, \overline { γ }\) ] = -1
(c) [ \(\overline { α }, \overline { ß }, \overline { γ }\) ] = 0
(d) [ \(\overline { α }, \overline { ß }, \overline { γ }\) ] = 2
Solution:
(c) [ \(\overline { α }, \overline { ß }, \overline { γ }\) ] = 0
Hint:
If \(\overline { α }\) lies in \(\overline { ß }\) & \(\overline { γ }\) plane
we have [ \(\overline { α }, \overline { ß }, \overline { γ }\) ] = 0
Question 3.
If \(\overline { a }\).\(\overline { b }\) = \(\overline { b }\).\(\overline { c }\) = \(\overline { c }\).\(\overline { a }\) = 0, then the value of [ \(\overline { a }, \overline { b }, \overline { c }\) ] is
(a) |\(\overline { a }\)| |\(\overline { b }\)| |\(\overline { c }\)|
(b) \(\frac { 1 }{ 3 }\)|\(\overline { a }\)| |\(\overline { b }\)| |\(\overline { c }\)|
(c) 1
(d) -1
Solution:
(a) |\(\overline { a }\)| |\(\overline { b }\)| |\(\overline { c }\)|
Hint:
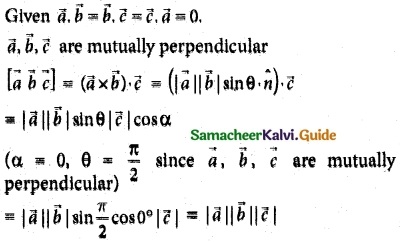
![]()
Question 4.
If \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) are three unit vectors such that \(\overline { a }\) is perpendicular to \(\overline { b }\) and is parallel to \(\overline { c }\) then \(\overline { a }\) × (\(\overline { b }\) × \(\overline { c }\)) is equal to
(a) \(\overline { a }\)
(b) \(\overline { b }\)
(c) \(\overline { c }\)
(d) \(\overline { 0 }\)
Solution:
(b) \(\overline { b }\)
Hint:

Question 5.
If [ \(\overline { a }, \overline { b }, \overline { c }\) ] = 1 then the value of
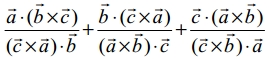
(a) 1
(b) -1
(c) 2
(d) 3
Solution:
(a) 1
Hint:
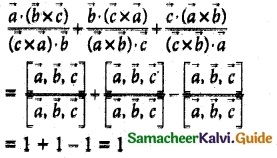
![]()
Question 6.
The volume of the parallelepiped with its edges represented by the vectors \(\hat { i }\) + \(\hat { j }\), \(\hat { i }\) + 2\(\hat { j }\), \(\hat { i }\) + \(\hat { j }\) + π\(\hat { k }\) is
(a) \(\frac { π }{ 2 }\)
(b) \(\frac { π }{ 3 }\)
(c) π
(d) \(\frac { π }{ 4 }\)
Solution:
(c) π
Hint:
\(\left|\begin{array}{lll}
1 & 1 & 0 \\
1 & 2 & 0 \\
1 & 1 & \pi
\end{array}\right|\) = π\(\left|\begin{array}{ll}
1 & 1 \\
1 & 2
\end{array}\right|\)
= π (2 – 1) = π
Question 7.
If \(\overline { a }\) and \(\overline { b }\) are unit vectors such that [\(\overline { a }\), \(\overline { b }\), \(\overline { a }\) × \(\overline { b }\)] = \(\frac { 1 }{ 4 }\), then the angle between \(\overline { a }\) and \(\overline { b }\) is
(a) \(\frac { π }{ 6 }\)
(b) \(\frac { π }{ 4 }\)
(c) \(\frac { π }{ 3 }\)
(d) \(\frac { π }{ 2 }\)
Solution:
(a) \(\frac { π }{ 6 }\)
Hint:

![]()
Question 8.
If \(\overline { a }\) = \(\hat { i }\) + \(\hat { j }\) + \(\hat { k }\), \(\overline { b }\) = \(\hat { i }\) + \(\hat { j }\), \(\overline { c }\) = \(\hat { i }\) and (\(\overline { a }\) × \(\overline { b }\))\(\overline { c }\) – λ\(\overline { a }\) + µ\(\overline { b }\) then the value of λ + µ is
(a) 0
(b) 1
(c) 6
(d) 3
Solution:
(a) 0
Hint:
\(\overline { a }\).\(\overline { c }\) = 1 and \(\overline { b }\).\(\overline { c }\) = 1
(\(\overline { a }\) × \(\overline { b }\))\(\overline { c }\) = (\(\overline { c }\) × \(\overline { a }\))\(\overline { b }\) – (\(\overline { c }\) × \(\overline { b }\))\(\overline { a }\) = λ\(\overline { a }\) + µ\(\overline { b }\)
⇒ µ = c; a = 1λ = -(\(\overline { c }\).\(\overline { b }\)) = -1
µ + λ = 1 – 1 = 0
Question 9.
If \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) are non-coplanar, non-zero vectors
such that [\(\overline { a }\), \(\overline { b }\), \(\overline { c }\)] = 3, then {[\(\overline { a }\) × \(\overline { b }\), \(\overline { b }\) × \(\overline { c }\), \(\overline { c }\) × \(\overline { a }\)]²} is equal to
is equal to
(a) 81
(b) 9
(c) 27
(d) 18
Solution:
(a) 81
Hint:
![]()
= 34 = 81
![]()
Question 10.
If \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) are three non-coplanar vectors such that \(\overline { a }\) × (\(\overline { b }\) × \(\overline { c }\)) = \(\frac { \overline{b}+\overline{c} }{ √2 }\) then the angle between \(\overline { a }\) and \(\overline { b }\) is
(a) \(\frac { π }{ 2 }\)
(b) \(\frac { 3π }{ 4 }\)
(c) \(\frac { π }{ 4 }\)
(d) π
Solution:
(b) \(\frac { 3π }{ 4 }\)
Hint:

Question 11.
If the volume of the parallelepiped with \(\overline { a }\) × \(\overline { b }\), \(\overline { b }\) × \(\overline { c }\), \(\overline { c }\) × \(\overline { a }\) as coterminous edges is 8 cubic units, then the volume of the parallelepiped with (\(\overline { a }\) × \(\overline { b }\)) × (\(\overline { b }\) × \(\overline { c }\)), (\(\overline { b }\) × \(\overline { c }\)) × (\(\overline { c }\) × \(\overline { a }\)) and (\(\overline { c }\) × \(\overline { a }\)) × (\(\overline { a }\) × \(\overline { b }\)) as coterminous edges is
(a) 8 cubic units
(b) 512 cubic units
(c) 64 cubic units
(d) 24 cubic units
Solution:
(c) 64 cubic units
Hint:
Given volume of the parallelepiped with
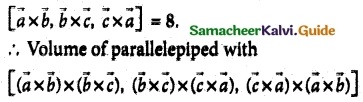
![]()
Question 12.
Consider the vectors \(\overline { a }\), \(\overline { b }\), \(\overline { c }\), \(\overline { d }\) such that (\(\overline { a }\) × \(\overline { b }\)) × (\(\overline { c }\) × \(\overline { d }\)) = \(\overline { 0 }\) Let P1 and P2 be the planes determined by the pairs of vectors \(\overline { a }\), \(\overline { b }\) and \(\overline { c }\), \(\overline { d }\) respectively. Then the angle between P1 and P2 is
(a) 0°
(b) 45°
(c) 60°
(d) 90°
Solution:
(a) 0°
Hint:
A vector perpendicular to the plane P1 of a, b is \(\overline { a }\) × \(\overline { b }\),
A vector perpendicular to the plane P2 of c and d is \(\overline { c }\) × \(\overline { d }\)
∴ (\(\overline { a }\) × \(\overline { b }\)) × (\(\overline { c }\) × \(\overline { d }\)) = 0
⇒ (\(\overline { a }\) × \(\overline { b }\)) || \(\overline { c }\) × \(\overline { d }\)
⇒ The angle between the planes is \(\overline { 0 }\)
Question 13.
If \(\overline { a }\) × (\(\overline { b }\) × \(\overline { c }\)) = (\(\overline { a }\) × \(\overline { b }\)) × \(\overline { c }\) where \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) are any three vectors such that \(\overline { b }\).\(\overline { c }\) ≠ 0 and \(\overline { a }\).\(\overline { b }\) ≠ 0, then \(\overline { a }\) and \(\overline { c }\) are
(a) perpendicular
(b) parallel
(c) inclined at angle \(\frac { π }{ 3 }\)
(d) inclined at an angle \(\frac { π }{ 6 }\)
Solution:
(b) parallel
Hint:

![]()
Question 14.
If \(\overline { a }\) = 2\(\hat { i }\) + 3\(\hat { j }\) – \(\hat { k }\), \(\overline { b }\) = \(\hat { i }\) + 2\(\hat { j }\) – 5\(\hat { k }\), \(\overline { c }\) = 3\(\hat { i }\) + 5\(\hat { j }\) – \(\hat { k }\) then \(\overline { a }\) vector perpendicular to a and lies in the plane containing \(\overline { b }\) and \(\overline { c }\) is
(a) -17\(\hat { i }\) + 21\(\hat { j }\) – 97\(\hat { k }\)
(b) 17\(\hat { i }\) + 21\(\hat { j }\) – 123\(\hat { k }\)
(c) -17\(\hat { i }\) – 21\(\hat { j }\) + 97\(\hat { k }\)
(d) -17\(\hat { i }\) – 21\(\hat { j }\) – 97\(\hat { k }\)
Solution:
(d) -17\(\hat { i }\) – 21\(\hat { j }\) – 97\(\hat { k }\)
Hint:
A vector ⊥r to \(\overline { a }\) and lies in the plane containing \(\overline { b }\) and \(\overline { c }\)
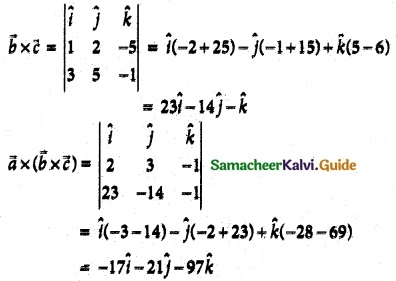
Question 15.
The angle between the lines \(\frac { x-2 }{ 3 }\) = \(\frac { y+1 }{ -2 }\), z = 2 and \(\frac { x-1 }{ 1 }\) = \(\frac { 2y+3 }{ 3 }\) = \(\frac { z+5 }{ 2 }\) is
(a) \(\frac { π }{ 6 }\)
(b) \(\frac { π }{ 4 }\)
(c) \(\frac { π }{ 3 }\)
(d) \(\frac { π }{ 2 }\)
Solution:
(d) \(\frac { π }{ 2 }\)
Hint:
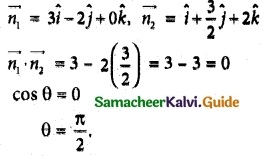
Question 16.
If the line \(\frac { x-2 }{ 3 }\) = \(\frac { y-1 }{ -5 }\) = \(\frac { z+2 }{ 2 }\) lies in the plane x + 3y – αz + ß = 0 then (α + ß) is
(a) (-5, 5)
(b) (-6, 7)
(c) (5, -5)
(d) (6, -7)
Solution:
(b) (-6, 7)
Hint:
\(\frac { x-2 }{ 3 }\) = \(\frac { y-1 }{ 5 }\) = \(\frac { z+2 }{ 2 }\) = λ ⇒ (3λ + 2, -5λ + 1, 2λ – 2)
which lie in x + 3y – αz + ß = 0
(3λ + 2) + 3(-5λ + 1) – α(2λ – 2) + ß = 0
3λ + 2 – 15λ + 3 – 2αλ + 2α + ß = 0.
(-12λ – 2αλ) + 2α + ß + 5 = 0.
-12λ – 2αλ = 0
2αλ = -12λ
α = -6
2α+ ß +5 = 0
-12 + ß + 5 = 0
ß – 7 = 0
ß = 7
(α, ß) = (-6, 7)
![]()
Question 17.
The angle between the line \(\overline { r }\) = (\(\hat { i }\) + 2\(\hat { j }\) – 3\(\hat { k }\)) + t(2\(\hat { i }\) + \(\hat { j }\) – 2\(\hat { k }\)) and the plane \(\overline { r }\) (\(\hat { i }\) + \(\hat { j }\)) + 4 = 0 is
(a) 0°
(b) 30°
(c) 45°
(d) 90°
Solution:
(c) 45°
Hint:

Question 18.
The co-ordinates of the point where the line \(\overline { r }\) = (6(\(\hat { i }\) – \(\hat { j }\) – 3\(\hat { k }\)) + t(-\(\hat { i }\) + \(\hat { k }\) meets the plane \(\overline { r }\) ((\(\hat { i }\) + (\(\hat { j }\) – (\(\hat { k }\)) = 3 are
(a) (2, 1, 0)
(b) (7, -1, -7)
(c) (1, 2, -6)
(d) (5, -1, 1)
Solution:
(d) (5, -1, 1)
Hint:
Given \(\overline { r }\) = (6(\(\hat { i }\) – (\(\hat { j }\) – 3(\(\hat { k }\)) + t(-(\(\hat { i }\) + (\(\hat { k }\))
\(\frac { x-6 }{ -1 }\) = \(\frac { y+1 }{ 0 }\) = \(\frac { z+3 }{ 4 }\) = t ⇒ (-t + 6, -1, 4t – 3)
which meets x + y – z = 3
-t + 6 – 1 – 4t + 3 = 3
-5t + 5 = 0
5t = 5
t = 1
∴ Co-ordinate is (5, -1, 1)
Question 19.
Distance from the origin to the plane 3x – 6y + 2z + 7 = 0 is
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(b) 1
Hint:
(x1, y1, z1) = (o, 0, o)
(a, b, c) = (3, -6, 2); d = 7.
d = \(\frac { ax_1+by_1+cz_1+d }{ \sqrt{a^2+b^2+c^2} }\) = \(\frac { 7 }{ \sqrt{9+36+4} }\) = \(\frac { 7 }{ 7 }\) = 1
![]()
Question 20.
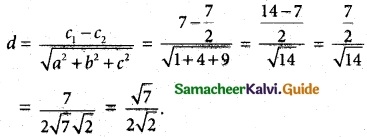
The distance between the planes
x + 2y + 3z + 7 = 0 and 2x + 4y + 6z + 7 = 0 is
(a) \(\frac { √7 }{ 2√2 }\)
(b) \(\frac { 7 }{ 2 }\)
(c) \(\frac { √7 }{ 2 }\)
(d) \(\frac { 7 }{ 2√2 }\)
Solution:
(a) \(\frac { √7 }{ 2√2 }\)
Hint:
x + 2y + 3z+7 = 0
2x + 4y + 6z + 7 = 0
(÷ 2) x + 2y + 3z + \(\frac { 7 }{ 2 }\) = 0
(1) and (2) are parallel planes
Question 21.
If the direction cosines of a line are \(\frac { 1 }{ c }\), \(\frac { 1 }{ c }\), \(\frac { 1 }{ c }\)
(a) c = ±3
(b) c = ±√3
(c) c > 0
(d) 0 < c < 1
Solution:
(b) c = ±√3
Hint:
cos²α + cos²ß + cos²γ = 1
\(\frac { 1 }{ c^2 }\) + \(\frac { 1 }{ c^2 }\) + \(\frac { 1 }{ c^2 }\) = 1
\(\frac { 3 }{ c ^2}\) = 1
c² = 3
c = ±√3
Question 22.
The vector equation \(\overline { r }\) = (\(\hat { i }\) – 2\(\hat { j }\) – \(\hat { k }\)) + t(6\(\hat { i }\) – \(\hat { k }\)) represents a straight line passing through the points
(a) (0, 6, -1) and (1, -2, -1)
(b) (0, 6, -1) and (-1, -4, -2)
(c) (1, -2, -1) and (1, 4, -2)
(d) (1, -2, -1) and (0, -6, 1)
Solution:
(c) (1, -2, -1) and (1, 4, -2)
Hint:
Given vector equation is

![]()
Question 23.
If the distance of the point (1, 1, 1) from the origin is half of its distance from the plane x + y + z + k = Q, then the values of k are
(a) ±3
(b) ±6
(c) -3, 9
(d) 3, -9
Solution:
(d) 3, -9
Hint:

Question 24.
If the planes \(\overline { r }\) (2\(\hat { i }\) – λ\(\hat { j }\) + \(\hat { k }\)) = 3 and \(\overline { r }\) (4\(\hat { i }\) + \(\hat { j }\) – µ\(\hat { k }\)) = 5 are parallel, then the value of λ and µ are
(a) \(\frac { 1 }{ 2 }\), -2
(b) –\(\frac { 1 }{ 2 }\), 2
(c) –\(\frac { 1 }{ 2 }\), -2
(d) \(\frac { 1 }{ 2 }\), 2
Solution:
(c) –\(\frac { 1 }{ 2 }\), -2
Hint:

![]()
Question 25.
If the length of the perpendicular from the origin to the plane 2x + 3y + λz = 1, λ > 0 is \(\frac { 1 }{ 5 }\), then the value of λ is
(a) 2√3
(b) 3√2
(c) 0
(d) 1
Solution:
(a) 2√3
Hint:
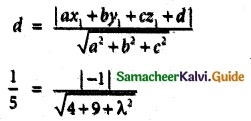
5 = \(\sqrt { 4+9+λ^2 }\)
25 = 4 + 9 + λ²
25 = 13 + λ²
λ² = 12
λ = 2√3