Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 4 Inverse Trigonometric Functions Ex 4.5 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.5
Question 1.
Find the value, if it exists. If not, give the reason for non-existence.
(i) sin-1 (cos π)
(ii) tan-1(sin(\(\frac {-5π}{2}\)))
(iii) sin-1 [sin 5]
Solution:
(i) sin-1 (cos π) = sin-1 (-1) = -sin-1 (1) = –\(\frac {π}{2}\) [∵ cos π = -1]
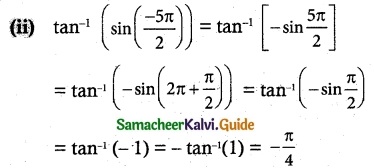
(iii) sin-1 [sin 5]
–\(\frac {π}{2}\) ≤ sin-1 5 ≤ \(\frac {π}{2}\)
-3\(\frac {π}{2}\) ≤ 5 ≤ 2π
–\(\frac {π}{2}\) ≤ 5 – 2π ≤ 0 ≤ \(\frac {π}{2}\)
sin(5 – 2π) = sin 5
sin-1 (sin 5) = 5 – 2π
![]()
Question 2.
Find the value of the expression in terms of x, with the help of a reference triangle.
(i) sin (cos-1(1 – x))
(ii) cos (tan-1 (3x – 1))
(iii) tan (sin-1(x + \(\frac {π}{2}\)))
Solution:
(i) sin (cos-1(1 – x)) = sin [cos-1(adj/hyp)]

(ii) cos (tan-1(3x – 1)) = cos [opp/adj]
Let θ = tan-1(3x – 1)
tan θ = 3x- 1
1 + tan² θ = 1 +(3x – 1)²
sec² θ = 9x² – 6x + 2
sec θ = \(\sqrt{9x² – 6x + 2}\)
cos θ = \(\frac{1}{\sqrt{9x² – 6x + 2}}\)
⇒ cos (tan-1(3x – 1)) = \(\frac{1}{\sqrt{9x² – 6x + 2}}\)
![]()

Question 3.
Find the value of
(i) sin-1(cos(sin-1(\(\frac {√3}{2}\))))
(ii) cot(sin-1 \(\frac {3}{5}\) + sin-1\(\frac {4}{5}\))
(iii) tan(sin-1 \(\frac {3}{5}\) + cot-1\(\frac {3}{2}\))
Solution:
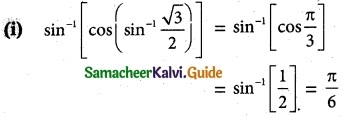


![]()
Question 4.
(i) tan-1\(\frac {2}{11}\) + tan-1 \(\frac {7}{24}\) = tan-1 \(\frac {1}{2}\)
(i) tan-1\(\frac {3}{5}\) + cos-1 \(\frac {12}{13}\) = sin-1 \(\frac {16}{65}\)
Solution:
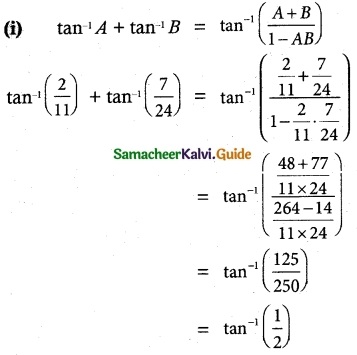

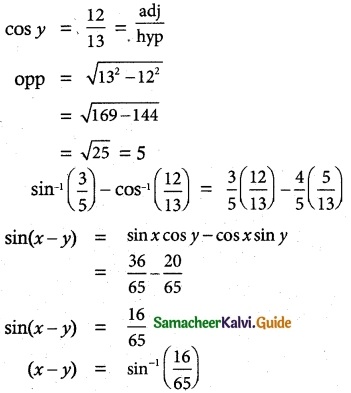
Question 5.
Prove that
tan-1 x + tan-1 y + tan-1 z = tan-1 (\(\frac {x+y+z-xyz}{1-xy-yz-zx}\))
Solution:
tan-1 x + tan-1 y + tan-1 z
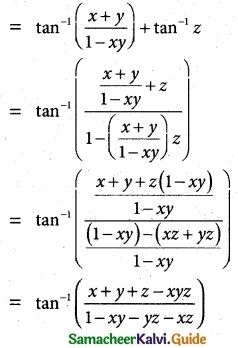
![]()
Question 6.
tan-1 x + tan-1 y + tan-1 z = π, show that x + y + z = xyz
Solution:
tan-1 x + tan-1 y + tan-1 z = π

x + y + z – xyz = 0
x + y + z = xyz
Question 7.
Prove that
tan-1 x + tan-1 \(\frac {2x}{1-x^2}\) = tan-1 \(\frac {3x-x^3}{1-3x^2}\), |x| < \(\frac {1}{√3}\)
Solution:
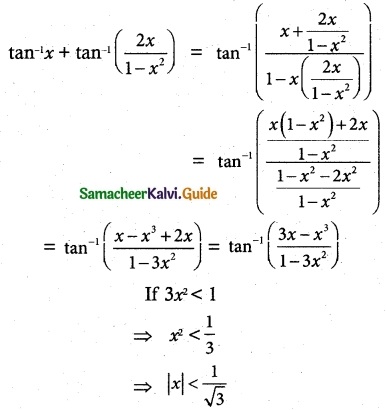
![]()
Question 8.
Simplify
tan-1 \(\frac {x}{y}\) – tan-1 \(\frac {x-y}{x+y}\)
Solution:

Question 9.
(i) sin-1 \(\frac {5}{x}\) + sin-1 \(\frac {12}{x}\) = \(\frac {π}{2}\)
(ii) 2 tan-1 x = cos-1 \(\frac {1-a^2}{1+a^2}\) – cos-1 \(\frac {1-b^2}{1+b^2}\), a > 0, b > 0
(iii) 2 tan-1 (cos x) = tan-1 (2 cosec x)
(iv) cot-1 x – cot-1 (x + 2) = \(\frac {π}{12}\), x > 0
Solution:
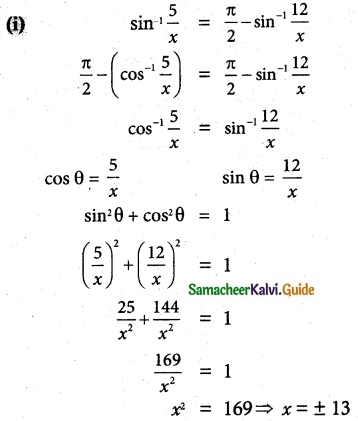

![]()

sin² x = sin x cos x
⇒ sin x cos x – sin² x = 0
⇒ sin x(cos x – sin x) = 0
sin x = 0 (or) cos x – sin x = 0
⇒ x = nπ, n ∈ Z, (or) cos x = sin x
tan x = 1 = tan \(\frac {π}{4}\)
⇒ x = nπ + \(\frac {π}{4}\), n ∈ Z
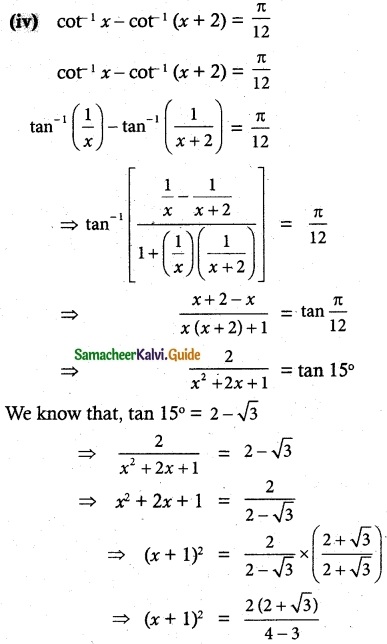
⇒ (x + 1)² = 4 + 2√3
⇒ (x + 1)² = 1 + 3 + 2√3
⇒ (x + 1)² = (1 + √3)²
⇒ x + 1 = 1 + √3
∴ x = √3
![]()
Question 10.
Find the number of the solutions of the equations
tan-1(x – 1) + tan-1 x + tan-1(x + 1) = tan-13x
Solution:
tan-1(x – 1) + tan-1 x + tan-1(x + 1)
= tan-1(x – 1) + tan-1(x + 1) + tan-1x

4x – x³ = 6x – 9x³
8x³ = 2x
8x³ – 2x = 0
2x(x² – 1) = 0
x = 0, x² = 1
x = ±1
Number of solutions are three (0, 1 -1)
![]()