Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 4 Inverse Trigonometric Functions Ex 4.2 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.2
Question 1.
Find all values of x such that
(j) -6π ≤ x ≤ 6π and cos x = 0
(ii) -5π ≤ x ≤ 5π and cos x = 1
Solution:
(i) cos x = 0
cos x = cos \(\frac {π}{2}\)
x = (2n + 1) \(\frac {π}{2}\), n = 0, ±1, ±2, ±3, ±4, ±5, -6
(ii) cos x = -1
cos x = cos π
x = (2n + 1) π, n = 0, ±1, ±2, -3
![]()
Question 2.
state the reason for cos -1 [cos(\(\frac {-π}{6}\))] ≠ –\(\frac {π}{6}\)
Solution:
cos -1 [cos(-\(\frac {π}{6}\))] = cos -1[ \(\frac {π}{6}\) ] = \(\frac {π}{6}\) ≠ \(\frac {-π}{6}\) ∉ [0, π]
Which is the principle domain of cosine function [∵ cos(-θ) = cos θ]
Question 3.
Is cos-1 (-x) = π – cos-1 true? justify your answer.
solution:
![]()
Question 4.
Find the principle value of cos-1(\(\frac {1}{2}\))
solution:
y = cos-1(\(\frac {1}{2}\))
cos-1x range is [0, π]
cos y = \(\frac {1}{2}\) = cos = \(\frac {π}{3}\)
y = \(\frac {π}{3}\) ∈ [0, π]
principle value is \(\frac {π}{3}\)
Question 5.
find the value of
(i) 2 cos-1 (\(\frac {1}{2}\)) + sin-1 (\(\frac {1}{2}\))
(ii) cos-1 (\(\frac {1}{2}\)) + sin-1(-1)
(iii) cos-1 (cos\(\frac {π}{2}\)cos\(\frac {π}{17}\) – sin\(\frac {π}{7}\)sin\(\frac {π}{17}\))
Solution:
(i) 2 cos-1 \(\frac {1}{2}\) + sin-1 \(\frac {1}{2}\)
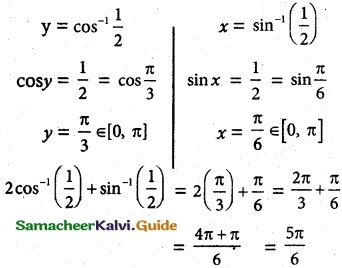
![]()
(ii) cos-1 \(\frac {1}{2}\) + sin-1(-1)
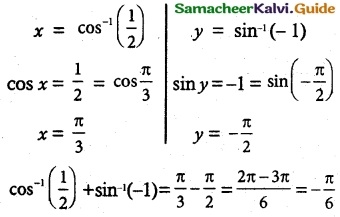
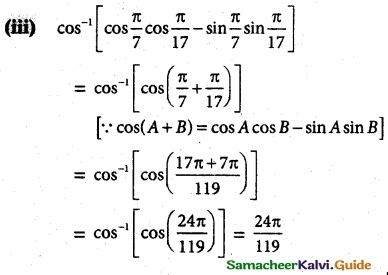
Question 6.
Find the domain of
(i) f(x) = sin-1 (\(\frac {|x|-2}{3}\)) + cos-1 (\(\frac {1-|x|}{4}\))
(ii) g(x) = sin-1 x + cos-1 x
Solution:
(i) -1 ≤ sin-1 (x) ≤ 1
-1 ≤ \(\frac {|x|-2}{3}\) ≤ 1
-3 ≤ |x| – 2 ≤ 3
-3 + 2 ≤ |x| ≤ 3 + 2
-1 ≤ |x| ≤ 5
|x| ≤ 5
since -1 ≤ |x| is not possible
-5 ≤ x ≤ 5 ………. (1)
By the definitions
-1 ≤ cos-1 (x) ≤ 1
-1 ≤ \(\frac {1-|x|}{4}\) ≤ 1
-4 ≤ 1 – |x| ≤ 4
-5 ≤ -|x| ≤ 3
-3 ≤ |x| ≤ 5
-3 ≤ |x| is not possible
-5 ≤ x ≤ 5 ………. (2)
From 1 and 2 we get
domain is x ∈ [-5, 5]
![]()
(ii) g(x) = sin-1 x + cos-1 x
range of sin x and cos x is [-1, 1]
-1 ≤ x ≤ 1
∴ x ∈ [-1, 1]
The domain of g(x) = [-1, 1]
Question 7.
For what value of x, the inequality
\(\frac {π}{2}\) < cos-1 (3x – 1) < π holds?
Solution:
\(\frac {π}{2}\) < cos-1 (3x – 1) < π
cos \(\frac {π}{2}\) < (3x – 1) < cos π
0 < 3x < 1 < -1
0 + 1 < 3x < -1 + 1
1 < 3x < 0
The inequality is true, only when
0 < x < \(\frac {1}{3}\)
![]()
Question 8.
Find the value of
(i) cos[cos-1(\(\frac {4}{5}\)) + sin-1(\(\frac {4}{5}\))]
(ii) (cos-1(cos \(\frac {4π}{3}\))) + cos-1(cos(\(\frac {5π}{4}\)))
Solution:
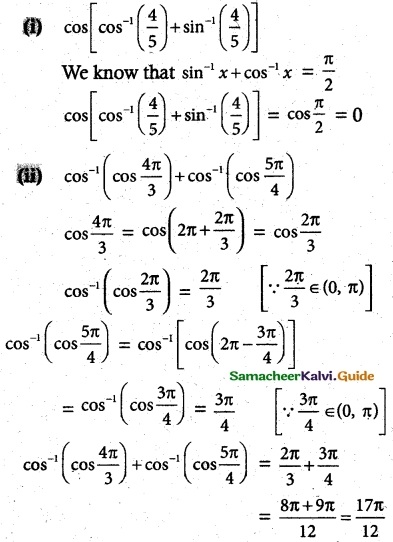
![]()