Samacheer Kalvi 12th Maths Guide Chapter 10 Ordinary Differential Equations Ex 10.8

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 10 Ordinary Differential Equations Ex 10.8 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.8

Question 1.
The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours, find how many bacteria will be present after 10 hours?
Solution:
Let x denote the number of bacteria at time t hours.
Given = \(\frac { dx }{ dt }\) = kx hence \(\frac { dx }{ x }\) = kdt
∴ x = C e^kt
Suppose x = x₀ at time t = 0
x₀ = C e^k(0) = C e° = C
∴ C = x₀
Hence x = x₀ e^kt
At time 5, x = 3x₀
(∵ Number triple in 5 hrs)
∴ Hence 3x₀ = x₀ e^5k
∴ e^5k = 3
when t = 10, x = x₀ e^10k = x₀ (e^5k)²
= x₀ 3² = 9x₀
∴ After 10 hours, the number of bacteria as 9 times the original number of bacteria.

Question 2.
Find the population of a city at any time t, given that the rate of increase of population is proportional to the population at that instant and that in a period of 40 years, the population increased from 3,00,000 to 4,00,000.
Solution:
Let P denote the population of a city
Given \(\frac { dP }{ dt }\) = kP
This equation can be written as
\(\frac { dP }{ P }\) = kdt
Taking integration on both sides, we get
∫ \(\frac { dP }{ P }\) = k∫ dt
log P = kt + log c
log P – log c = kt
log (\(\frac { P }{ c }\)) = kt
\(\frac { P }{ c }\) = e^kt
P = ce^kt …….. (1)
Initial condition:
Given when t = 0 ; P = 3,00,000
Equation (1) becomes,
3.0. 000 = ce^k(0) = ce°
3,00,000 = c [∵ e° = 1]
∴ (1) ⇒ P = 3,00,000 e^kt ………. (2)
Again when t = 40; P = 4,00,000
Equation (2) becomes,
4,00,000 = 3,00,000 e^40k
\(\frac { 4,00,000 }{ 3,00,000 }\) = e^40k
\(\frac { 4 }{ 3 }\) = e^40k
Taking log,
log(\(\frac { 4 }{ 3 }\)) = 40k
k = \(\frac { 1 }{ 40 }\) log \(\frac { 4 }{ 3 }\)
k = log(\(\frac { 4 }{ 3 }\))^{\(\frac { 1 }{ 40 }\)} [∵ n log m = log mⁿ]
Substituting k values in equation (2), we get
P = 3,00,000 e^{log(\(\frac { 4 }{ 3 }\))\(\frac { 1 }{ 40 }\)}
P = 3,00,000 (\(\frac { 4 }{ 3 }\))^{\(\frac { 1 }{ 40 }\)} [∵ e^{log a x} = a^x]

Question 3.
The equation of electromotive force for an electric circuit containing resistance and self-inductance is E = Ri + L\(\frac { di }{ dt }\), where E is the electromotive force is given to the circuit, R the resistance and L, the coefficient of induction. Find the current i at time t when E = 0.
Solution:

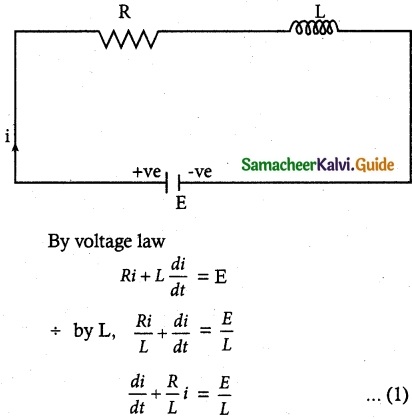
This is a linear differential equation.
Integrating factor I.F = e^{∫ \(\frac { R }{ L }\)dt} = e^{\(\frac { R }{ L }\)t}
Its solution is given by

Question 4.
The engine of a motorboat moving at 10 m/s is shut off. Given that the retardation at any subsequent time (after shutting off the engine) equal to the velocity at that time. Find the velocity after 2 seconds of switching off the engine.
Solution:
Let v be the velocity
Given the engine of a motorboat moving 10 m/s.
After that the engine is shut off then the acceleration is negative.
So it be \(\frac { -dv }{ dt }\)
i.e., \(\frac { dv}{ dt}\) = -v
The equation can be written as taking integration on both sides, we get
\(\frac { dv}{ dt}\) = -dt
∫ \(\frac { dv}{ v }\) = ∫-dt
log v = -t + log c
log v – log c = -t
log (\(\frac { v }{ c }\)) = -t
\(\frac {v}{c}\) = e^-t
v = ce^-t ……….. (1)
Initial condition
Given that when t = 0, v = 10 m/sec i
substituting in equation (1), we get !
10 = ce^-0
10 = ce°
10 = c
∴ c = 10
(1) ⇒ v = 10e^-t
when t = 2 find v
v = 10 e^-2
v = \(\frac {10}{e^2}\)
The velocity after 2 seconds is \(\frac {10}{e^2}\)
i.e., v = \(\frac {10}{e^2}\)

Question 5.
Suppose a person deposits 10,000 Indian rupees in a bank account at the rate of 5% per annum compounded continuously. How much money will be in his bank account 18 months later?
Solution:
Let P be the principal amount
Given Rate of interest = 5% per annum.
∴ \(\frac {dp}{dt}\) = p(\(\frac {5}{100}\)) = 0.05P
The equation can be written as,
\(\frac {dP}{P}\) = 0.05 dt
Taking Integration on both sides, we get
∫\(\frac {dP}{P}\) = 0.051 ∫dt
log P = 0.05 t + log c
log P – log C = 0.05t
log (\(\frac {P}{C}\)) = 0.05 t
\(\frac {P}{C}\) = e^0.05t
P = C e^0.05t ………. (1)
Initial condition:
Given when t = 0; P = 10,000
Substituting these values in equation (1), we get
P = C e^0.05t
10,000 = C e^{0.05 (0)}
10,000 = C e°
C = 10,000
∴ Substituting the C value in equation (1), we get
P = 10,000 e^0.05t ……. (2)
When t= 18 months = 1\(\frac {1}{2}\)yr =3/2 years, we get
(2) ⇒ P = 10,000 e^{0.05 (3/2)}
P = 10,000 e^0.075
The amount in a bank account be
P = 10,000 e^0.075

Question 6.
Assume that the rate at which radioactive nuclei decay is proportional to the number of such nuclei that are present in a given sample. In a certain sample, 10% of the original number of radioactive nuclei have undergone disintegration in a period of 100 years. What percentage of the original radioactive nuclei will remain after 1000 years?
Solution:
Let N be the sample radioactive nuclei at any time t & N₀ be the radioactive nuclei at the initial time.
Given \(\frac {dN}{dt}\) = -kN
Where k > 0 is a constant
The equation can be written as
\(\frac {dN}{N}\) = -kdt
Taking integration on both sides, we get
∫\(\frac {dN}{N}\) = ∫-kdt
log N = -kt + log C
log N – log C = -kt
log(\(\frac {N}{C}\)) = -kt
\(\frac {N}{C}\) = e^-kt
N = Ce^-kt ……… (1)
Initial condition:
when t = 0 we have N = N₀
N₀ = Ce^-k(0)
N₀ = Ce⁰
N₀ = C
Substituting C value in equation (1), we get ;
N = N₀ e^-kt ……… (2)
Given: In a certain sample 10% of the original number of radioactive nuclei have undergone disintegration in a period of 100 years be when t = p₀

Equation (2) becomes

The percentage of the original radioactive nuclei of remain after 1000 years is
\(\frac {N}{N_0}\) × 100 = (\(\frac {9}{10}\))¹⁰ × 100 = \(\frac {9^{10}}{10^{10}}\) × 10²
= \(\frac {9^{10}}{10^{8}}\) %

Question 7.
Water at temperature 100°C cools in 10 minutes to 80° C at a room temperature of 25°C. Find
(i) The temperature of the water after 20 minutes
(ii) The time when the temperature is 40° C
[log, \(\frac {11}{15}\) = -0.3101; log_e 5 = 1.6094]
Solution:
We apply “Newton’s law of cooling” while states that the rate of decrease of the temperature of a body is proportional to the difference between the temperature of the body and that of the medium.
\(\frac {dT}{dt}\) = -k(T – T₀)
Where T is the temperature of the body at time t & T₀ the constant temperature of the medium.
Thus \(\frac {dT}{dt}\) = -k(T – 25) or
\(\frac {dT}{T-25}\) = -kdt
On Integrating equation (1), we get
∫\(\frac {dT}{T-25}\) = ∫-kdt
log (T – 25) = -kt + c₁
Now T = 100, t = 0
log (100 – 25) = -k (0) + c₁
∴ log 75 = c₁
Substituting c₁ value in equation (1), we get
log (T – 25) = -kt + log 75
∵ log m – log n = log m/n
log \(\frac {T-25}{75}\) = kt ……. (2)
Also T = 80 when t = 10 minutes

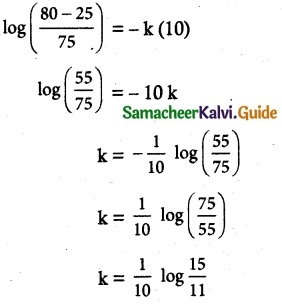
Substituting k value in equation (2), we get

T = 75 (0.5378) + 25
T = 40.33 + 25
T = 65.33°C

Question 8.
At 10.00 A.M. a woman took a cup of hot instant coffee from her microwave oven and placed it on a nearby kitchen counter to cool. At this instant, the temperature of the coffee was 180° F and 10 minutes later it was 160° F. Assume that the constant temperature of the kitchen was 70° F.
(i) What was the temperature of the coffee at 10.15 AM?
The woman likes to drink coffee when its temperature is between 130° F and 140° F. Between what times should she have drunk the coffee?
Solution:
Let T be the temperature of a coffee at time t.
T_k be the temperature of the kitchen
By Newton’s law of cooling

Initial condition:
when t = 0; T = 180°F
180 = ce^k(0) + 70
180 = ce° + 70
180 – 70 = c
∴ c = 110°
Substituting c value in equation (1), we get
T = ce^+kt + 70
T = 100 e^kt + 70 …….. (2)
Second condition:
when t = 10, T = 160
(2) ⇒ 160 = 110 e^10k + 70
160 – 70= 110 e^10k

T = 81.33 + 70
T = 151.3 F
∴ The temperature of the coffee at 10.15 A.M is 151.3° F

(ii) Woman’s like to drink a coffee between 130°F and 140°F.
(a) when T = 130°F
(2) ⇒ T = 110 e^kt + 70
130 – 70 = 110 e^kt
\(\frac { 60 }{ 110 }\)
\(\frac { 6 }{ 11 }\) = e^kt

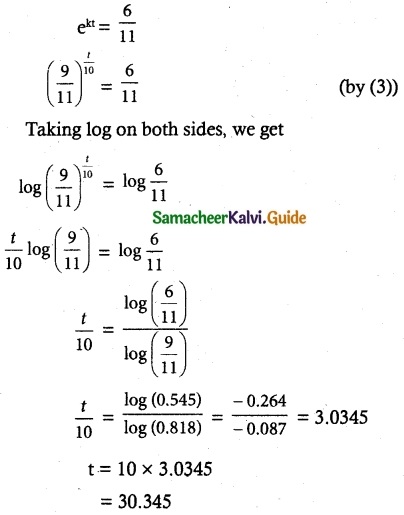
b) When T = 140°
(2) ⇒ T = 110e^kt + 70
160 – 70 = 110 e^kt

t = 22.6 min
She drinks coffee between 10.22 & 10.30 approximately.

Question 9.
A pot of boiling water at 100° C is removed from a stove at time t = 0 and left to cool in the kitchen. After 5 minutes, the water temperature has decreased to 80° C and another 5 minutes later it has dropped to 65° C. Determine the temperature of the kitchen.
Solution:
Let T be the temperature of the boiling water.
T_m is the temperature of the kitchen.
By Newton’s law of cooling, we get
\(\frac { dT }{ dt }\) = k (T – T_m)
The equation can be written as
Taking Integration on both sides, we get


(a – b)² = a² + b² – 2ab
a = 80 b = T_m
6400 + T\(_{m}^{2}\) – 160 T_m = 6500 – 100 T_m – 65 T_m + T\(_{m}^{2}\)
6400 – 6500 = 160 T_m – 165 T_m
– 100 = – 5T_m
T_m = \(\frac { 100 }{ 5 }\)
T_m = 20°C
Hence the temperature of the kitchen be 20° C

Question 10.
A tank initially contains 50 litres of pure water. Starting at time t = 0 a brine containing 2 grams of dissolved salt per litre flows into the tank at the rate of 3 litres per minute. The mixture is kept uniform by stirring and the well-stirred mixture simultaneously flows out of the tank at the same rate. Find the amount of salt present in the tank at any time t > 0.
Solution:
Let x be the amount of salt in the tank at time t.
∴ \(\frac { dx }{ dt }\) = inflow rate – outflow rate ……… (1)
Given 2 grams of dissolved salt per litre flows into the tank at the rate of 3 litres per minute.
(i.e) inflow rate contain = 6 gram salt
[∵ for one litre = 2 gram salt]
[for 3 litre = 6 gram salt]
tank contain 50 litres of water
∴ out flow of rate of salt = \(\frac { 3x }{ 50 }\)
substitute inflow rate and outflow rate in equation (1), we get