Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 3 Integral Calculus II Ex 3.3 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 3 Integral Calculus II Ex 3.3
Question 1.
Calculate consumer’s surplus if the demand function p = 50 – 2x and x = 20
Solution:
Demand function p = 50 – 2x and x = 20
when x = 20, p = 50 – 2(20)
p = 50 – 40 = 10
∴ p0 = 10
CS = \(\int _{0}^{x}\) (demand function) dx – (Price × quantity demanded)
= \(\int _{0}^{20}\) (50 – 2x)dx – (10 × 20)
= [50x – 2(\(\frac { x^2 }{2}\))]\( _{0}^{20}\) – 200
= [50x – x²]\( _{0}^{20}\) – 200
= {50(20) – (20)² – [0]} – 200
= (1000 – 400) – 200
= 600 – 200
∴ C.S = 400 units
![]()
Question 2.
Calculate consumer’s surplus if the demand function p = 122 – 5x – 2x² and x = 6.
Solution:
Demand function p = 122 – 5x – 2x² and x = 6
when x = 6; p = 122 – 5(6) – 2(6)²
= 122 – 30 – 2 (36)
= 122 – 102 = 20
∴ p0 = 20
C.S = \(\int _{0}^{x}\) (demand function) dx – (Price × quantity demanded)
= \(\int _{0}^{6}\)(122 – 5x – 2x²) dx – (20 × 6)
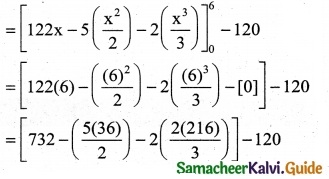
[732 – 5(18) – 2(72)] – 120
= 732 – 90 – 144 – 120
= 732 – 354 = 378
∴ CS = 378 units
![]()
Question 3.
The demand function p = 85 – 5x and supply function p = 3x – 3. Calculate the equilibrium price and quantity demanded. Also calculate consumer’s surplus.
Solution:
Demand function p = 85 – 5x
Supply function p = 3x – 35
W.K.T. at equilibrium prices pd = ps
85 – 5x = 3x – 35
85 + 35 = 3x + 5x
120 = 8x ⇒ x = \(\frac { 120 }{8}\)
∴ x = 15
when x = 15 p0 = 85 – 5(15) = 85 – 75 = 10
C.S = \(\int _{0}^{x}\) f(x) dx – x0p0
= \(\int _{0}^{x}\) (85 – 5x) dx – (15)(10)
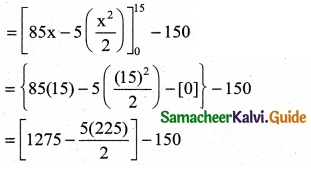
= 1275 – \(\frac { 1125 }{2}\) – 150
= 1275 – 562.50 – 150
= 1275 – 712.50
∴ CS = 562.50 units
Question 4.
The demand function for a commodity is p = e-x. Find the consumer’s surplus when p = 0.5
Solution:
The demand function p = e-x
when p = 0.5 ⇒ 0.5 = e-x
\(\frac { 1 }{2}\) = \(\frac { 1 }{e^x}\) ⇒ ex = 2
∴ x = log 2
∴ Consumer’s surplus
C.S = \(\int _{0}^{x}\) (demand function) dx – (Price × quantity demanded)
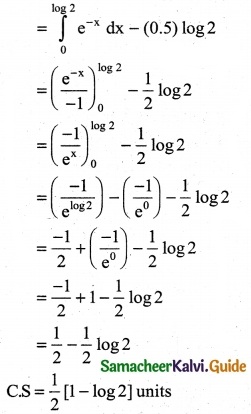
![]()
Question 5.
Calculate the producer’s surplus at x = 5 for the supply function p = 7 + x
Solution:
The supply function p = 7 + x
when x = 5 ⇒ p = 7 + 5 = 12
∴ x0 = 5 and p0 = 12
Producer’s surplus

Question 6.
If the supply function for a product is p = 3x + 5x². Find the producer’s surplus when x = 4
Solution:
The supply function p = 3x + 5x²
when x = 4 ⇒ p = 3(4) + 5(4)²
p = 12 + 5(16)= 12 + 80
p = 92
∴ x0 = 4 and p0 = 92
Producer’s Surplus

![]()
Question 7.
The demand function for a commodity is p = \(\frac { 36 }{x+4}\) Find the producer’s surplus when the prevailing market price is Rs 6.
Solution:
The demand function for a commodity
p = \(\frac { 36 }{x+4}\)
when p = 6 ⇒ 6 = \(\frac { 36 }{x+4}\)
x + 4 = \(\frac { 36 }{6}\) ⇒ x + 4 = 6
x = 2
∴ p0 = 6 and x0 = 2
The consumer’s surplus
C.S = \(\int _{0}^{x}\) f(x) dx – x0p0
= \(\int _{0}^{2}\) (\(\frac { 36 }{x+4}\)) dx – 2(6)
= 36 [log (x + 4)]\(_{0}^{2}\) – 12
= 36 [log (2 + 4) – log (0 + 4)] – 12
= 36 [log6 – log4] – 12
= 36[log(\(\frac { 6 }{4}\))] – 12
∴ CS = 36 log(\(\frac { 6 }{4}\)) – 12 units
![]()
Question 8.
The demand and supply functions under perfect competition are pd = 1600 – x² and ps = 2x² + 400 respectively, find the producer’s surplus.
Solution:
pd = 1600 – x² and ps = 2x² + 400
Under the perfect competition pd = ps
1600 – x² = 2x² + 400
1600 – 400 = 2x² + x² ⇒ 1200 = 3x²
⇒ x² – 400 ⇒ x = 20 or -20
The value of x cannot be negative, x = 20 when x0 = 20;
p0 = 1600 – (20)² = 1600 – 400
P0 = 1200
PS = x0p0 – \(\int _{0}^{x_0}\) g(x) dx

![]()
Question 9.
Under perfect competition for a commodity the demand and supply laws are Pd = \(\frac { 8 }{x+1}\) – 2 and Ps = \(\frac { x+3 }{2}\) respectively. Find the consumer’s and producer’s surplus.
Solution:

16 – (x² + 3x + x + 3) = 2 [2(x + 1)]
16 – (x² + 4x + 3) = 4(x + 1)
16 – x² – 4x – 3 = 4x + 4
x² + 4x + 4x + 4 + 3 – 16 = 0
x² + 8x – 9 = 0
(x + 9) (x – 1) = 0 ⇒ x = -9 (or) x = 1
The value of x cannot be negative x = 1 when x0 = 1
p0 = \(\frac { 8 }{1+1}\) – 2 ⇒ p0 = \(\frac { 8 }{2}\) – 2
p0 = 4 – 2 ⇒ p0 = 2
CS = \(\int _{0}^{x}\) f(x) dx – x0p0
= \(\int _{0}^{1}\) (\(\frac { 8 }{x+1}\) – 2) dx – (1) (2)
= {8[log(x + 1)] – 2x}\(\int _{0}^{1}\) – 2
= 8 {[log (1 + 1) – 2(1)] – 8 [log (0 + 1) – 2(0)]} – 2
= [8 log (2) – 2 – 8 log1] – 2
= 8 log(\(\frac { 8 }{2}\)) – 2 – 2
C.S = (8 log 2 – 4) units
P.S = x0p0 – \(\int _{0}^{x_0}\) g(x) dx

![]()
Question 10.
The demand equation for a products is x = \(\sqrt {100-p}\) and the supply equation is x = \(\frac {p}{2}\) – 10. Determine the consumer’s surplus and producer’s, under market equilibrium.
Solution:
pd = \(\sqrt {100-p}\) and ps = \(\sqrt {100-p}\)
Under market equilibrium, pd = ps
\(\sqrt {100-p}\) = \(\frac {p}{2}\) – 10
Squaring on both sides
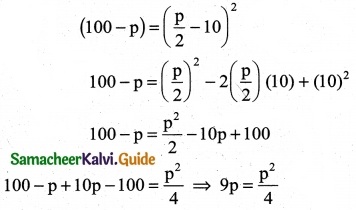
36p = p² ⇒ p² – 36 p = 0
p (p – 36) = 0 ⇒ p = 0 or p = 36
The value of p cannot be zero, ∴p0 = 36 when p0 = 36
x0 = \(\sqrt {100-36}\) = \(\sqrt {64}\)
∴ x0 = 8

= 288 – [x² + 20x]\( _{0}^{8}\)
= 288 – { [(8)² + 20(8)] – [0]}
= 288 – [64 + 160]
= 288 – 224 = 64
PS = 64 Units
![]()
Question 11.
Find the consumer’s surplus and producer’s surplus for the demand function pd = 25 – 3x and supply function ps = 5 + 2x
Solution:
pd = 25 – 3x and ps = 5 + 2x
Under market equilibrium, pd = ps
25 – 3x = 5 + 2x
25 – 5 = 2x + 3x ⇒ 5x = 20
∴ x = 4
when x = 4
P0 = 25 – 3(4)
= 25 – 12 = 13
p0 = 13

= 52 – [5x + x²]\( _{0}^{4}\)
= 52 – (5(4) + (4)²) – (0)}
= 52 – [20 + 16]
= 52 – 36
∴ PS = 16 units
![]()
Read More: