Samacheer Kalvi 12th Business Maths Guide Chapter 10 Operations Research Ex 10.2

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 10 Operations Research Ex 10.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 10 Operations Research Ex 10.2

Question 1.
What is the Assignment problem?
Solution:
Suppose that we have ‘m1 jobs to be performed on ‘n’ machines. The cost of assigning each job to each machine is C_ij (i = 1, 2, … n and j = 1, 2, … , n). Our objective is to assign the different jobs to the different machines (one job per machine) to minimize the overall cost. This is known as assignment problem.

Question 2.
Give mathematical form of assignment problem.
Solution:
Consider the problem of assigning n jobs to n machines (one job to one machine). Let C_ij be the cost of assigning i^th job to the j^th machine and x_ij represents the assignment of i^th job to the j^th machine.

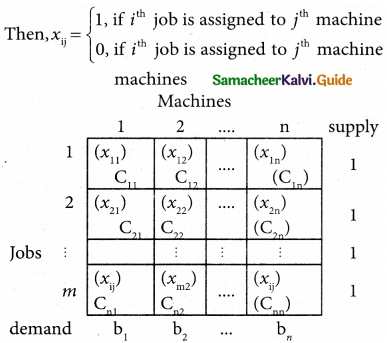
x_ij is missing in any cell means that no assignment is made between the pair of job and machine.(i.e) x_ij = 0.
x_ij is presents in any cell means that an assignment is made their. In such cases x_ij = 1
The assignment model can written in LPP as follows
Minimize Z = \(\sum_{i=1}^{m}\) \(\sum_{j=1}^{n}\) C_ij x_ij
Subject to the constrains
\(\sum_{i=1}^{n}\) x_ij = 1, j = 1, 2, …. n
\(\sum_{j=1}^{n}\) x_ij = 1, i = 1,2,….n and x_ij =0 (or) 1 for all i, j

Question 3.
What is the difference between Assignment Problem and Transportation Problem?
Solution:

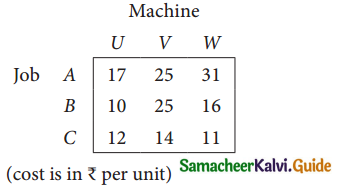
Question 4.
Three jobs A, B and C one to be assigned to three machines U, V and W. The processing cost for each job machine combination is shown in the matrix given below. Determine the allocation that minimizes the overall processing cost.
(cost is in Rs per unit)

Solution:
Here the number of rows and columns are equal.
∴ The given assignment problem is balanced.
Step 1.
Select the smallest element in each row and subtract this from all the elements in its row.

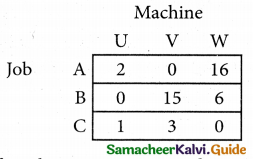
Look for atleast one zero in each row and each column.
Here each and every row and columns having exactly one zero No need step 2 go to step 3.

Step 3.

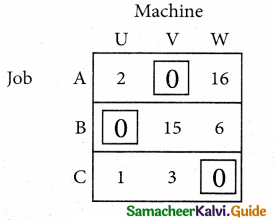
Mark the zero by □ Mark other zeros in its column by X.
Since each row and each column contains exactly one assignment, all the three machine have been assigned a job.

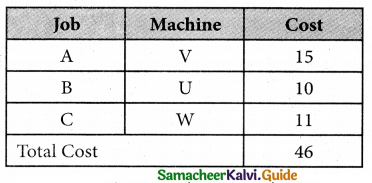
The Optimal assignment (minimum) cost = 46

Question 5.
A computer centre has got three expert programmers. The centre needs three application programmes to be developed. The head of the computer centre, after studying carefully the programmes to be developed, estimates the computer time in minitues required by the experts to the application programme as follows.

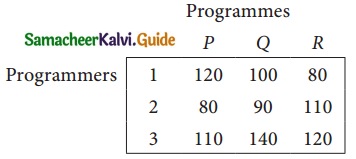
Assign the programmers to the programme in such a way that the total computer time is least.
Solution:
Here the number of rows and columns are equal.
∴ The given assignment problem is balanced.
Step 1.
Select the smallest element in each row and subtract this from all the elements in its row.

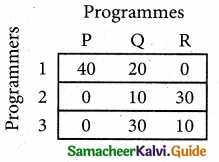
Step 2.
Select the smallest element in each column and subtract this from all the elements in its column.

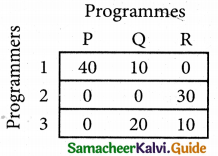
Step 3. (Assignment)
Examine the rows with exactly one zero, mark the zero by □. Mark other zeros in its column by X.

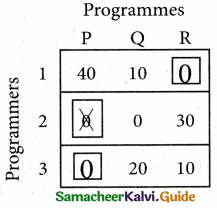
Step: 4
Now examine the columns with exactly one zero mark the zero by □. Mark other zeros in its row by X.

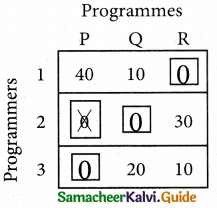
Thus all the three assignment have been made. The optimal assignment schedule and total cos is

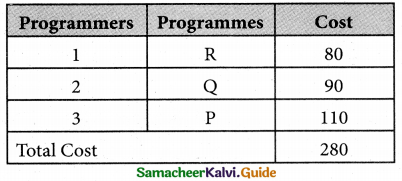
The optimal assignment (minimum) cost = Rs 280

Question 6.
A departmental head has four subordinates and four tasks to be performed. The subordinates differ in efficiency and the tasks differ in their intrinsic difficulty. His estimates of the time man would take to perform each task is given below.

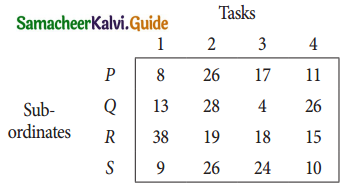
How should the tasks to allocated to subordinates so as to minimize the total man-hours?
Solution:
Here the number of rows and columns are equal.
∴ The given assignment problem is balanced.
Step 1.
Select the smallest element in each row and subtract this from all the elements in its row.

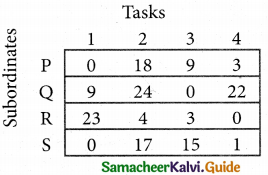
Step 2.
Select the smallest element in each column and subtract this from all the elements in its column.

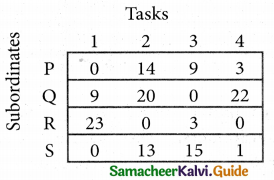
Step 3. (Assignment)
Examine the rows with exactly one zero Mark the zero by □. Mark other zeros in its row by X.

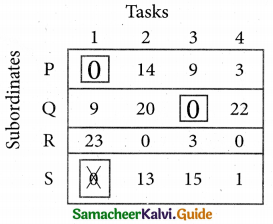
Step 4.
Now examine the columns with exactly one zero. Mark the zero by □ Mark other zeros in its row by X.

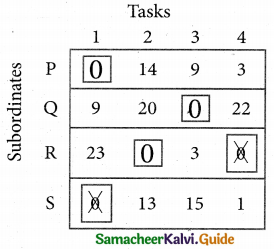
Step 5.
Cover all the zeros of table 4 with three lines, since three assignments were made check (✓) row S since it has no assignment.

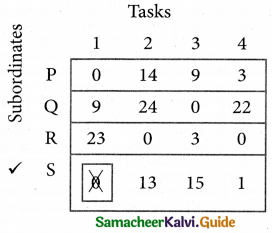
Step 6.
Develop the new revised tableau. Examine those elements that are not covered by a line in table 5. Take the smallest element. This is 1 (one) our case. By subtracting 1 from the uncovered cells.

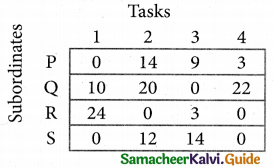
[Adding 1 to elements (Q, S, R) that line at the intersection of two lines]

Step 7.
Go to step 3 and repeat the procedure until you arrive at an optimal assignment.

Step 8.
Determine an assignment.

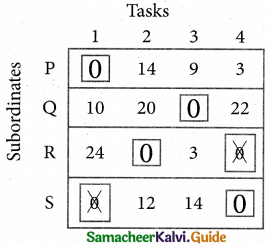
Thus all the four assignment have been made. The optimal assignment schedule and total time is

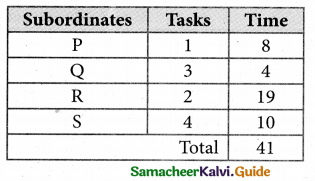
The optimum time (minimum) = 41 Hrs.

Question 7.
Find the optimal solution for the assignment problem with the following cost matrix.

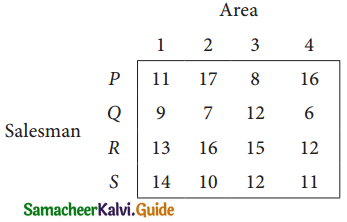
Solution:
Here the number of rows and columns are equal.
∴ The given assignment problem is balanced.
Step 1.
Select the smallest element in each row and subtract this from all the elements in its row.

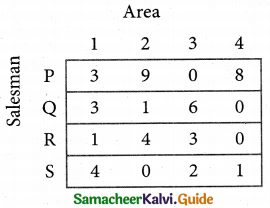
Step 2.
Select the smallest element in each column and sub tract this from all the elements in its column.

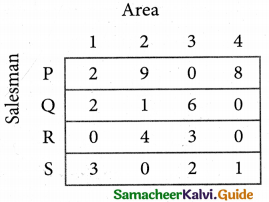
Step 3. (Assignment)
Examine the rows with exactly one zero. Mark the zero by □ Mark other zeros in its column by X

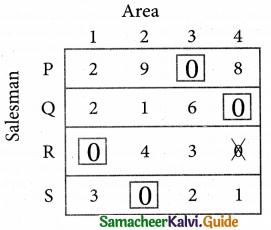
Thus all the four assignments have been made. The optimal assignment schedule and total cost.

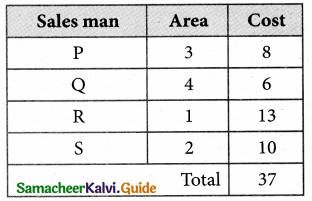
The Optimum cost (minimum) = Rs 37

Question 8.
Assign four trucks 1, 2, 3 and 4 to vacant spaces A, B, C, D, E and F so that distance travelled is minimized. The matrix below shows the distance.

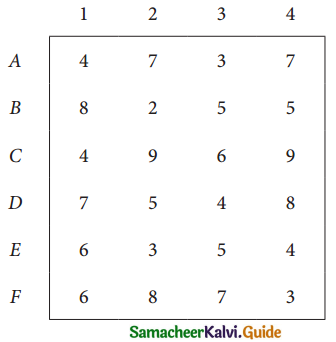
Solution:
Since the number of columns is less than the number of rows, the given assignment problem is unbalanced one. To balance it, introduce two dummy columns with all the entries zeros.
The revised assignment problem is

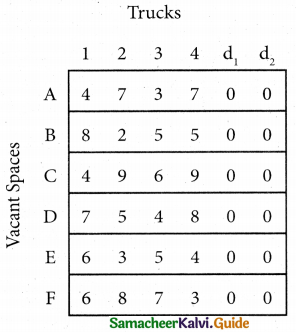
Here only 4 tasks can be assigned to 4 vacant spaces.
Step 1.
It is not necessary, since each row contains zero entry. Go to step 2.

Step 2.
Select the smallest element in each column and subtract this from all the elements in its column.

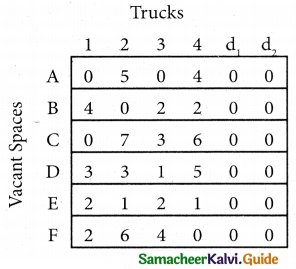
Step 3. (Assignment)
Since each row contains more than one zeros. Go to step 4.

Step 4.
Examine the columns with exactly one zero, mark the zero by □ Mark other zeros in its rows by X.

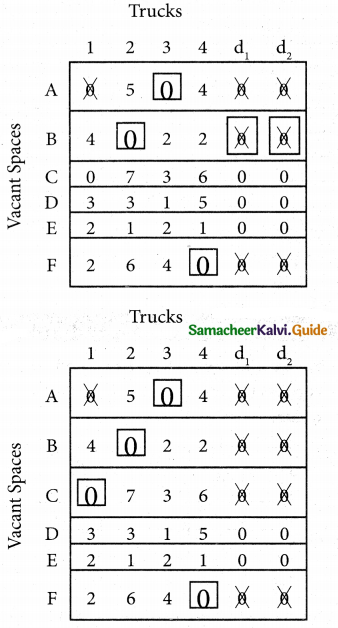
Step 5.
Here all the four assignments have been made we can assign d₁ for D then we will get d₂ for E.

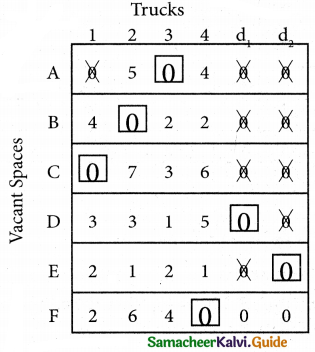
The optimal assignment schedule and total distance is

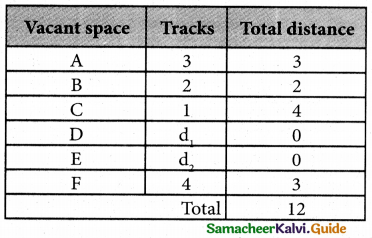
∴ The Optimum Distant (minimum) = 12 units