Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 Trigonometry Ex 3.8 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.8
Question 1.
Find the principal solution and general solutions of the following
(i) sin θ = – \(\frac{1}{\sqrt{2}}\)
(ii) cot θ = √3
(iii) tan θ = –\(\frac{1}{\sqrt{3}}\)
Answer:
(i) sin θ = – \(\frac{1}{\sqrt{2}}\)
We know that principal of sin θ lies in \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\)
sin θ = – \(\frac{1}{\sqrt{2}}\) < 0
∴ The principal value of sin θ lies in the IV quadrant.
sin θ = – \(\frac{1}{\sqrt{2}}\)
= – sin \(\left(\frac{\pi}{4}\right)\)
sin o = sin \(\left(-\frac{\pi}{4}\right)\)
Hence θ = \(-\frac{\pi}{4}\) is the principal solution.
The general solution is
θ = nπ + (- 1)n . \(\left(-\frac{\pi}{4}\right)\) , n ∈ Z
θ = nπ + (- 1)n + 1 . \(\frac{\pi}{4}\) , n ∈ Z
![]()
(ii) cot θ = √3

The principal value of tan θ lies in \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
Since tan θ = \(\frac{1}{\sqrt{3}}\) > 0
The principal value of tan θ lies in the I quadrant.
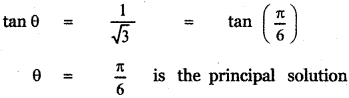
The general solution of tan θ is
θ = nπ + \(\frac{\pi}{6}\) , n ∈ Z
(iii) tan θ = –\(\frac{1}{\sqrt{3}}\)
The principal value of tan θ lies in \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
Since tan θ = – \(\frac{1}{\sqrt{3}}\) > 0
The principal value of tan θ lies in the IV quadrant.
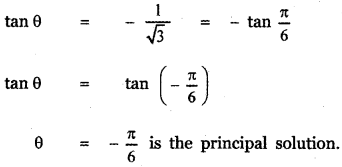
The general solution of tan θ is
θ = nπ – \(\frac{\pi}{6}\) , n ∈ Z
![]()
Question 2.
Solve the following equations for which solutions lies in the interval 0° ≤ 9 < 360°
(i) sin4x = sin2x
Answer:
sin4x – sin2x = 0
sin2 x (sin2 x – 1) = 0
sin2 x [ – (1 – sin2 x)] = 0
sin2x × – cos2x = 0
– sin2x cos2x = 0
(sin x cos x)2 = 0
(\(\frac { 1 }{ 2 }\) × 2 sin cos x)2 = 0
\(\frac { 1 }{ 4 }\) sin 2x = 0
sin 2x = 0
The general solution is
2x = nπ, n ∈ Z
x = \(\frac{\mathrm{n} \pi}{2}\), n ∈ Z
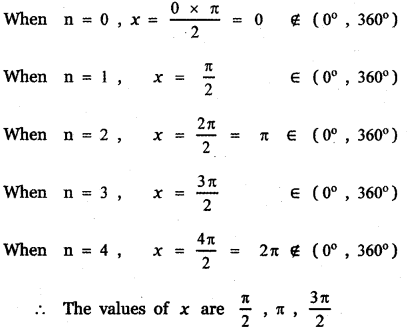
![]()
(ii) 2 cos2x + 1 = – 3 cos x
Answer:
2 cos2x + 1 = – 3 cos x
2 cos2x + 3 cos x + 1 = 0
2 cos2x + 2 cos x + cos x + 1 = 0
2 cos x (cos x + 1) + 1 (cos x + 1) = 0
(2 cos x + 1) (cos x + 1) = 0
2 cos x + 1 = 0 or cos x + 1 = 0
cos x = \(-\frac{1}{2}\) or cos x = – 1
To find the solution of cos x = \(-\frac{1}{2}\)
cos x = \(-\frac{1}{2}\)

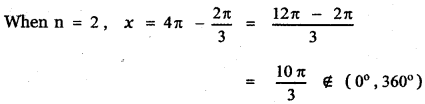
To find the solution of cos x = – 1
cos x = – 1
cos x = cos π
The general solution is
x = 2nπ ± π, n ∈ Z
x = 2nπ + π or x = 2nπ – π, n ∈ Z
Consider x = 2nπ + π
when n = 0 , x = 0 + π = π ∈ (0°, 360°)
when n = 1 , x = 2π + π = 3π ∉ (0°, 360°)
Consider x = 2nπ – π
when n = 0, x = 0 – π ∉ (0°, 360°)
when n = 1, x = 2π – π = π ∈ (0°, 360°)
when n = 2, x = 4π – π = 3π ∉ (0°, 360°)
∴ The required solution are x = \(\frac{2 \pi}{3}\), \(\frac{4 \pi}{3}\), π
![]()
(iii) 2 sin2x + 1 = 3 sin x
Answer:
2 sin2x – 3 sin x + 1 = 0
2 sin2x – 2 sin x – sin x + 1 = 0
2 sin x (sin x – 1) – 1 (sin x – 1) = 0
(2 sin x – 1)(sin x – 1) = 0
2 sin x – 1 = 0 or sin x – 1 = 0
sin x = \(\frac { 1 }{ 2 }\) or sin x = 1
To find the solution of sin x = \(\frac { 1 }{ 2 }\)
sin x = \(\frac { 1 }{ 2 }\)
sin x = sin \(\left(\frac{\pi}{6}\right)\)
The general solution is x = nπ + (-1)n\(\frac{\pi}{6}\), n ∈ z

![]()
(iv) cos2x = 1 – 3 sin x
Answer:
1 – 2 sin2x = 1 – 3 sinx
2 sin2 x – 3 sin x = 0
sin x(2 sin x – 3) = 0smx =
sin x = 0 or 2 sin x – 3 = 0
sin x = 0 or sin x = \(\frac{3}{2}\)
sin x = \(\frac{3}{2}\) is not possible since sin x ≤ 1
∴ sin x = 0 = sin 0
The general solution is x = nit ,
When n = 0, x = 0 ∉ (0°, 360°)
When n = 1, x = π ∈ (0°, 360°)
When n = 2, x = 2π ∉ (0°, 360°)
∴ The required solutions is x = π
![]()
Question 3.
Solve the following equations:
(i) sin 5x – sin x = cos 3x
Answer:
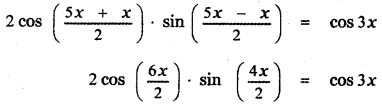
2 cos 3 x . sin 2x = cos 3 x
2 cos 3x . sin 2x – cos3x = 0
cos 3x (2 sin 2x – 1) = 0
cos 3x = 0 or 2 sin 2x – 1 = 0
cos 3x = 0 or sin 2x = \(\frac { 1 }{ 2 }\)
To find the general solution of cos 3x = 0
The general solution of cos 3x = 0 is
3x = (2n + 1)\(\frac{\pi}{2}\), n ∈ Z
x = (2n + 1)\(\frac{\pi}{6}\), n ∈ Z
To find the general solution of sin 2x = \(\frac{1}{2}\)
sin 2x = \(\frac{1}{2}\)
sin 2x = sin \(\left(\frac{\pi}{6}\right)\)
The general solution is
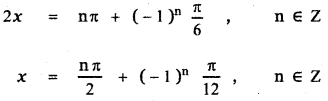
∴ The required solutions are
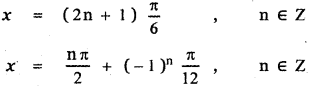
![]()
(ii) 2 cos2θ + 3 sin θ – 3 = θ
Answer:
2 cos2θ + 3 sin θ – 3 = θ
2(1 – sin2θ)+ 3 sin θ – 3 = θ
2 – 2 sin2θ + 3 sin θ – 3 = θ
– 2 sin2θ + 3 sin θ – 1 = θ
2 sin2 θ – 3 sin θ + 1 = θ
2 sin2θ – 2 sin θ – sin θ + 1 = θ
2 sin θ (sin θ – 1) – (sin θ – 1) = θ
(2 sin θ – 1) (sin θ – 1) = 0
2 sin θ – 1 = 0 or sin θ – 1 = θ
sin θ = \(\frac { 1 }{ 2 }\) or sin θ = 1
To find the general solution of’ sin θ = \(\frac { 1 }{ 2 }\)
sin θ = \(\frac { 1 }{ 2 }\)
sin θ = sin \(\frac{\pi}{6}\)
The general solution is θ = nπ + (-1)n\(\frac{\pi}{6}\), n ∈ Z
To find the general solution of sin θ = 1
sin θ = 1
sin θ = \(\frac{\pi}{2}\)
The general solution is θ = nπ + (-1)n\(\frac{\pi}{2}\), n ∈ Z
∴ The required solutions are
θ = nπ + (-1)n\(\frac{\pi}{6}\), n ∈ Z (or)
θ = nπ + (-1)n\(\frac{\pi}{6}\), n ∈ Z
![]()
(iii) cos θ + cos 3θ = 2 cos 2θ
Answer:
cos 3θ + cos θ = 2 cos 2θ
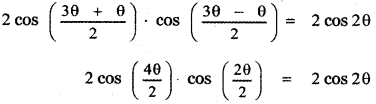
2 cos 2θ . cos θ = 2 cos 2θ
cos 2θ . cos θ – cos 2θ = θ
cos 2θ (cos θ – 1) = θ
cos 2θ = θ or cos θ – 1 = θ
cos 2θ = θ or cos θ = 1
To find the general solution of cos 2θ = θ
The general solution is
2θ = (2n + 1)\(\frac{\pi}{2}\), n ∈ Z
θ = (2n + 1)\(\frac{\pi}{4}\), n ∈ Z
To find the general solution of cos θ = 1
cos θ = 1
cos θ = cos 0
The general solution is θ = 2nπ , n ∈ Z
∴ The required solutions are
θ = (2n + 1)\(\frac{\pi}{4}\), n ∈ Z (or)
θ = 2nπ, n ∈ Z
![]()
(iv) sin θ + sin 3θ + sin 5θ = 0
Answer:
sin 5θ + sin 3θ + sin θ = 0
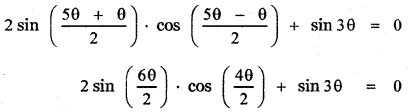
2 sin 3θ . cos 2θ + sin 3θ = 0
sin 3θ (2 cos 2θ + 1) = θ
sin 3θ = 0 or 2 cos 2θ + 1 = θ
sin 3θ = 0 or cos 2θ = –\(\frac { 1 }{ 2 }\)
To find the general solution of sin 3θ = 0
The general solution is
3θ = nπ, n ∈ Z
θ = \(\frac{\mathbf{n} \pi}{3}\), n ∈ Z
To find the general solution of cos 2θ = –\(\frac { 1 }{ 2 }\)
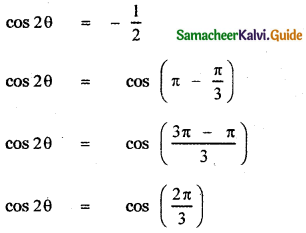
The general solution is
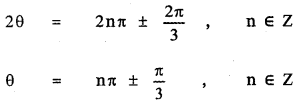
∴ The required solutions are

![]()
(v) sin 2θ – cos 2θ – sin θ + cos θ = θ
Answer:


![]()
(vi) sin θ + cos θ = √2
Answer:

The general solution is
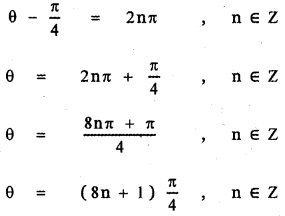
![]()
(vii) sin θ + √3 cos θ = 1
Answer:
Divide each term by 2

![]()
(viii) cot θ + cosec θ = √3
Answer:



![]()
(ix) tan θ + tan \(\left(\theta+\frac{\pi}{3}\right)\) + tan \(\left(\theta+\frac{2 \pi}{3}\right)\) = √3
Answer:
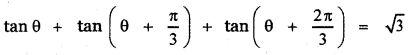


![]()
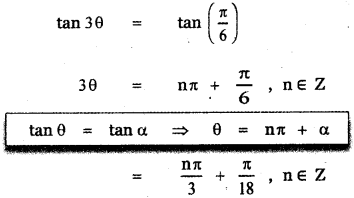
(x) cos 2θ = \(\frac{\sqrt{5}+1}{4}\)
Answer:
we know cos 36° = \(\frac{\sqrt{5}+1}{4}\), 36° = \(\frac{\pi}{5}\)
cos 2θ = cos 36° = cos \(\left(\frac{\pi}{5}\right)\)
The general solution is
2θ = 2nπ ± \(\frac{\pi}{5}\), n ∈ Z
θ = nπ ± \(\frac{\pi}{10}\), n ∈ Z
![]()
(xi) 2cos 2x – 7 cos x + 3 = 0
Answer:
2 cos2x – 7 cos x + 3 = 0
2 cos2x – 6 cos x – cos x + 3 = 0
2 cos x (cos x – 3) – 1 (cos x – 3) = 0
(2 cos x – 1) (cos x – 3) = 0
2 cos x – 1 = 0 or cos x – 3 = 0
cos x = \(\frac { 1 }{ 2 }\) or cos x = 3
Since – 1 ≤ cos x ≤ 1 , we have
cos x = 3 is not possible.
∴ cos x = \(\frac { 1 }{ 2 }\)
cos x = cos \(\frac{\pi}{3}\)
The general solution is x = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z