Samacheer Kalvi 11th Maths Guide Chapter 3 Trigonometry Ex 3.6

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 Trigonometry Ex 3.6 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.6

Question 1.
Express each of the following as a sum or difference.
(i) sin 35°. cos 28°
(ii) sin 4x cos 2x
(iii) 2 sin 10θ . cos 2θ
(iv) cos 5θ . cos 2θ
(v) sin 5θ . sin 4θ
Answer:
(i) sin 35°. cos 28°
We know
sin A cos B = \(\frac { 1 }{ 2 }\) [sin (A + B) + sin (A – B)]
Take A = 35° and B = 28°
sin 35°cos 28° = \(\frac { 1 }{ 2 }\)[sin(35° + 28°) + sin(35° – 28°)]
sin 350 cos 28° = \(\frac { 1 }{ 2 }\)[sin 63° + sin 7°]

(ii) sin 4x cos 2x
We know
sin A cos B = \(\frac { 1 }{ 2 }\) [sin (A + B) + sin (A – B )]
Take A = 4x , B = 2x
sin 4x . cos 2x = \(\frac { 1 }{ 2 }\)[sin(4x + 2x) + sin(4x – 2x)]
sin 4x . cos 2x = \(\frac { 1 }{ 2 }\)[sin 6x + sin 2x]

(iii) 2 sin 10θ . cos 2θ
We know
2 sin A cos B = sin (A + B) + sin (A – B)
Take A = 10θ, B = 2θ
2 sin 10θ . cos 2θ = sin (10θ + 2θ) + sin (10θ – 2θ)
2 sin 10θ. cos 2θ = sin 12 θ + sin 8θ
2 sin 10θ . cos 2θ = \(\frac { 1 }{ 2 }\)[sin 12θ + sin 8θ]

(iv) cos 5θ . cos 2θ
We know .
cosA cosB = \(\frac { 1 }{ 2 }\) [cos (A + B) + cos (A – B)]
Take A = 5θ, B = 2θ
cos 5θ . cos 2θ = \(\frac { 1 }{ 2 }\) [cos (5θ + 2θ) + cos(5θ – 2θ)]
cos 5θ . cos 2θ = \(\frac { 1 }{ 2 }\) [cos 7θ + cos 3θ]

(v) sin 5θ . sin 4θ
we know
sin A sin B = \(\frac { 1 }{ 2 }\) [cos (A – B) – cos (A + B)]
Take A = 5θ, B = 4θ
sin 5θ . sin 4θ = \(\frac { 1 }{ 2 }\) [cos (5θ – 4θ) – cos (5θ + 4θ)]
sin 5θ . sin 4θ = \(\frac { 1 }{ 2 }\) [cos θ – cos 9θ]

Question 2.
Express each of the following as a product.
(i) sin 75° sin 35°
(ii) cos 65° + cos 15°
(iii) sin 50° + sin 40°
(iv) cos 35° – cos 75°
Answer:
(i) sin 75° sin 35°

(ii) cos 65° + cos 15°

(iii) sin 50° + sin 40°
We know

(iv) cos 35° – cos 75°
We know

Question 3.
Show that sin 12° . sin 48° . sin 54° = \(\frac{1}{8}\)
Answer:
sin 12° . sin 48° . sin 54° = sin 48° . sin 12°. sin (90° – 36°)
= \(\frac { 1 }{ 2 }\) [cos (48° – 12°) – cos (48° + 12°)] cos 36°
= \(\frac { 1 }{ 2 }\) [cos 36° – cos 6o°] cos 36°
= \(\frac { 1 }{ 2 }\) [cos 36° – \(\frac { 1 }{ 2 }\)] cos 36°
= \(\frac { 1 }{ 2 }\) [cos²36° – \(\frac { 1 }{ 2 }\) cos 36°]

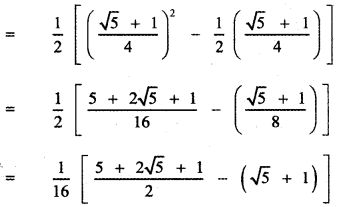
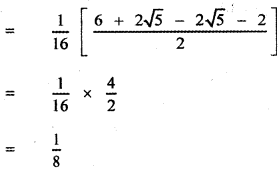
Question 4.
Show that

Answer:

Question 5.
Show that

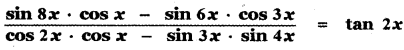
Answer:

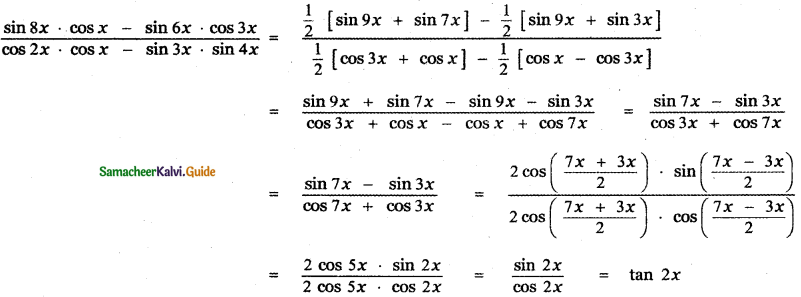
Question 6.
Show that

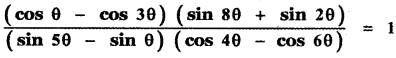
Answer:

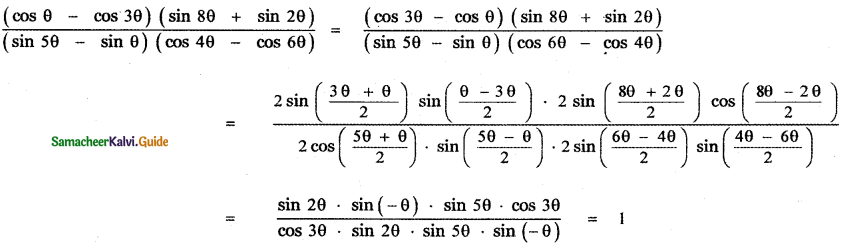
Question 7.
Prove that sin x + sin 2x + sin 3x = sin 2x (1 + 2 cos x)
Answer:
sin x + sin 2x + sin 3x = sin x + 2 sin x cos x + 3 sin x – 4 sin³ x
= sin x [1 + 2 cos x + 3 – 4 sin² x]
= sin x [2 cos x + 4 – 4 sin² x ]
= sin x [2 cosx + 4(1 – sin²x)]
= sin x [2 cos x + 4 cos²x]
= 2 sin x cos x [1 + 2 cos x]
= sin 2x (1 + 2 cosx)

Question 8.
Prove that

Answer:

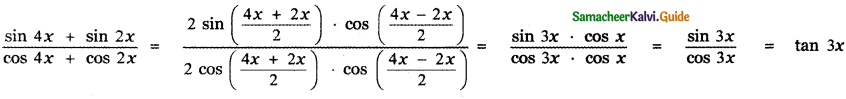
Question 9.
Prove that 1 + cos 2x + cos 4x + cos 6x = 4 cos x . cos 2x . cos 3x
Answer:
4 cos x cos 2x . cos 3x = 4 cos x . cos 3x . cos 2x = 4 cos x . [cos (3x + 2x) + cos (3x – 2x)]
2 cos x. [cos 5x + cos x] = 2 cos 5x . cos x + 2 cos² x
= 2 × \(\frac { 1 }{ 2 }\) [cos (5x + x) + cos (5x – x)] + 1 + cos 2x
= cos 6x + cos 4x + 1 + cos 2x
= 1 + cos 2x + cos 4x + cos 6x

Question 10.
Prove that

Answer:

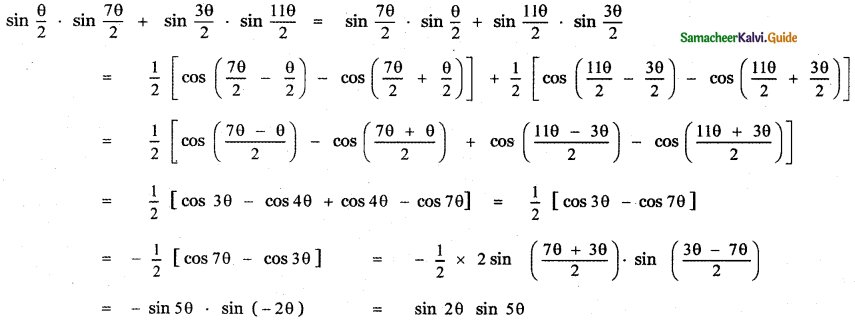
Question 11.
Prove that cos (30°- A) cos (30° + A) + cos (45° – A). cos(45° + A) = cos 2A + \(\frac { 1 }{ 4 }\)
Answer:
cos(30° – A) cos(30° + A) + cos(45° – A) . cos(45° + A)
= cos (30° + A) cos (30°- A) + cos (45° + A) cos (45° – A)
= \(\frac { 1 }{ 2 }\) [cos (30° + A + 30° – A) + cos ( 30° + A – (30° + A ))] + \(\frac { 1 }{ 2 }\) [cos (45° + A + 45° – A) + cos (45° + A – (450 + A))
= \(\frac { 1 }{ 2 }\) [cos 60° + cos (30° + A – 30° + A)] + \(\frac { 1 }{ 2 }\)[cos 90° + cos(45° + A – 45° + A)]
= \(\frac { 1 }{ 2 }\)[cos 60° + cos 2A] + \(\frac { 1 }{ 2 }\)[cos 90° + 2A]
= \(\frac { 1 }{ 2 }\) cos 60° + \(\frac { 1 }{ 2 }\) cos 2A + \(\frac { 1 }{ 2 }\) cos 90° + \(\frac { 1 }{ 2 }\) cos 2A
= \(\frac { 1 }{ 2 }\) × \(\frac { 1 }{ 2 }\) + cos 2A + \(\frac { 1 }{ 2 }\) × o
= \(\frac { 1 }{ 4 }\) + cos 2A

Question 12.
Show that

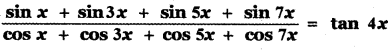
Answer:

Question 13.
Prove that

Answer:

Question 14.
Show that cot (A + 15°) – tan (A – 15°) = \(\frac{4 \cos 2 A}{1+2 \sin 2 A}\)
Answer: