Samacheer Kalvi 11th Maths Guide Chapter 3 Trigonometry Ex 3.3

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 Trigonometry Ex 3.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.3

Question 1.
Find the values of
(i) sin 480°
(ii) sin (-1110°)
(iii) cos 300°
(iv) tan (1050°)
(v) cot 660°
(vi) tan \(\left(\frac{19 \pi}{3}\right)\)
(vii) sin \(\left(\frac{-11 \pi}{3}\right)\)
Answer:
(i) sin(480°) = sin(360° + 120°) = sin 120°
= sin(90° + 30°) = cos 30° = \(\sqrt{3}\)/2

(ii) sin(-1110°) = -sin(1110°)
= – sin (360° × 3 + 30°)
= -sin 30° = -1/2

(iii) cos(300°) = cos(270° + 30°) = sin 30° = 1/2

(iv) tan (1050°)
tan (1050°) = tan(12 × 90 – 30°)
= – tan30° = – \(\frac{1}{\sqrt{3}}\)

(v) cot 660°
cot 660° = cot (7 × 90 + 30°)
= – tan 30° = – \(\frac{1}{\sqrt{3}}\)

(vi) tan \(\left(\frac{19 \pi}{3}\right)\)

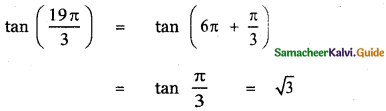
(vii) sin \(\left(\frac{-11 \pi}{3}\right)\)

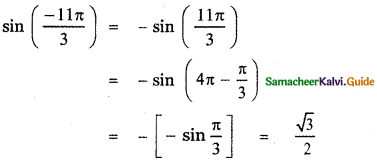
Question 2.
\(\left(\frac{5}{7}, \frac{2 \sqrt{6}}{7}\right)\) is a point on the terminal side of an angle θ in standard position. Determine the six trigonometric function values of angle θ.
Answer:
Given \(\left(\frac{5}{7}, \frac{2 \sqrt{6}}{7}\right)\) is a point on the terminal side of an angle θ in standard position.

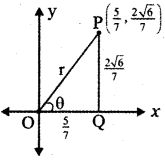
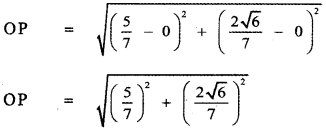
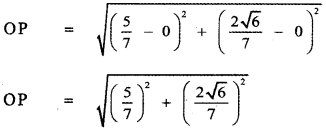
Question 3.
Find the values of the other five trigonometric functions of the following
(i) cos θ = –\(\frac{1}{2}\), θ lies in the III quadrant
(ii) cos θ = \(\frac{2}{3}\), θ lies in the I quadrant
(iii) sin θ = –\(\frac{2}{3}\), θ lies in the IV quadrant
(iv) tan θ = – 2, θ lies in the II quadrant
(v) sec θ = \(\frac{13}{5}\), θ lies inthe IVquadrant
Answer:
(i) cos θ = –\(\frac{1}{2}\), θ lies in the III quadrant

(ii) cos θ = \(\frac{2}{3}\), θ lies in the I quadrant
We know that cos²θ + sin²θ = 1
\(\left(\frac{2}{3}\right)^{2}\) + sin²θ = 1
\(\frac{4}{9}\) + sin²θ = 1

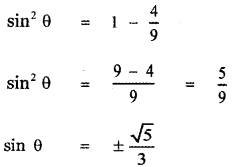
Since θ lies in the I quadrant all trigonometric functions are positive.

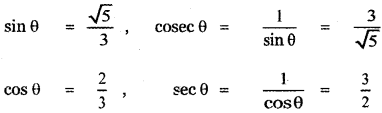
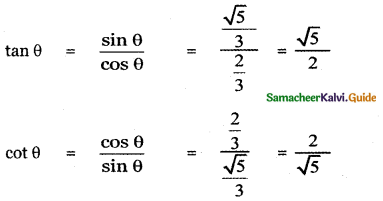
(iii) sin θ = –\(\frac{2}{3}\), θ lies in the IV quadrant
We know that cos²θ + sin²θ = 1
cos²θ + \(\left(-\frac{2}{3}\right)^{2}\) = 1
cos²θ + \(\frac{4}{9}\) = 1

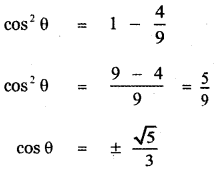
Since θ lies in the fourth quadrant cos θ is positive.

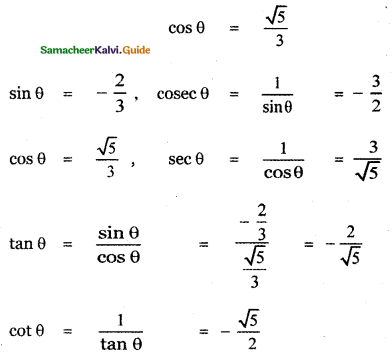
(iv) tan θ = – 2, θ lies in the II quadrant
We know that sec²θ – tan²θ = 1
sec²θ – (-2)² = 1
sec²θ – 4 = 1
sec²θ = 1 + 4 = 5
sec θ = ± √5
Since θ lies in the second quadrant sec θ is negative.

(v) sec θ = \(\frac{13}{5}\), θ lies inthe IVquadrant
We know that sec²θ – tan²θ = 1
\(\left(\frac{13}{5}\right)^{2}\) – tan²θ = 1
\(\frac{169}{25}\) – 1 = tan²θ

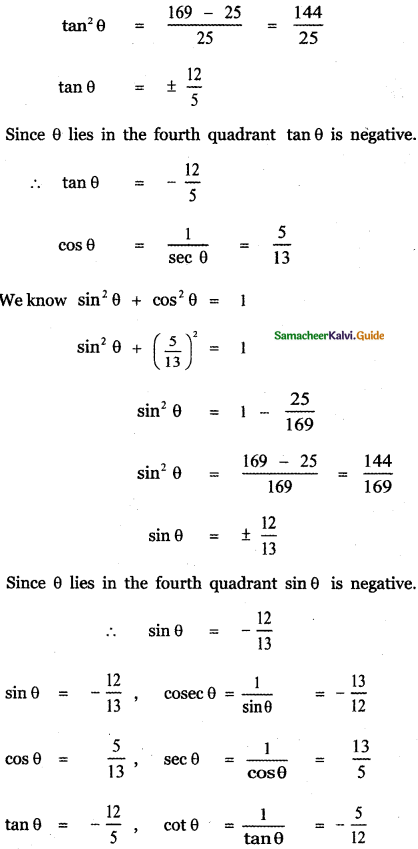
Question 4.
Prove that

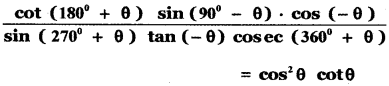
Answer:

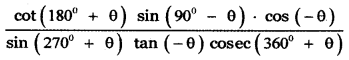
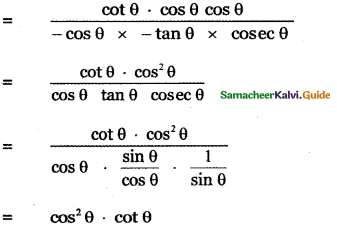
Question 5.
Find all the angles between 0° and 360° which satisfy the equation sin²θ = \(\frac{3}{4}\)
Answer:
sin²θ = \(\frac{3}{4}\) ⇒ sin θ = ± \(\frac{\sqrt{3}}{2}\)
sin 60° = \(\frac{\sqrt{3}}{2}\)
sin 120° = sin (180° – 60°)
= sin 60° = \(\frac{\sqrt{3}}{2}\)
∴ θ = 60° and 120°

Question 6.
Show that

Answer:

= sin² 10° + sin² 20° + [cos 20°]² + [cos 10°]²
= sin² 10° + sin² 20° + cos² 20° + cos² 10°
= sin² 10° + cos² 10° + sin² 20° + cos² 20°
= 1 + 1 = 2