Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 3 Trigonometry Ex 3.2 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.2
Question 1.
Express each of the following in radian measure.
(i) 30°
(ii) 135°
(iii) -205°
(iv) 150°
(v) 330°
Answer:
(i) 30°

![]()
(ii) 135°
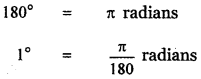
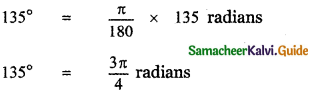
(iii) – 205°

(iv) 150°

![]()
(v) 330°

Question 2.
Find the degree measure corresponding to the following radian measures.
(i) \(\frac{\pi}{3}\)
(ii) \(\frac{\pi}{9}\)
(iii) \(\frac{2 \pi}{5}\)
(iv) \(\frac{7 \pi}{3}\)
(v) \(\frac{10 \pi}{9}\)
Answer:
(i) \(\frac{\pi}{3}\) radians

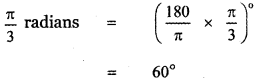
![]()
(ii) \(\frac{\pi}{9}\) radians

(iii) \(\frac{2 \pi}{5}\) radians

(iv) \(\frac{7 \pi}{3}\) radians

(v) \(\frac{10 \pi}{9}\) radians

![]()
Question 3.
What must be the radius of a circular running path, around which an athlete must run 5 times in order to describe 1 km?
Answer:
Let the radius of the circular path be = r m.
Length of the circular path s = 1 k. m
s = 1000 m.
Athlete runs 5 times around the path to cover 1 k. m distance
∴ θ = 360° × 5
θ = 360° × 5 × \(\frac{\pi}{180}\) radians
θ = 10 π radians
s = r θ
1000 = r 10 π
r = \(\frac{1000}{10 \pi}\)
r = \(\frac{1000 \times 7}{10 \times 22}=\frac{350}{11}\)
r = 31 .818 meters
Radius of the circular path = 31 .82 meters
![]()
Question 4.
In a circle of diameter 40 cm a chord is of length 20 cm. Find the length of the minor arc of the chord.
Answer:
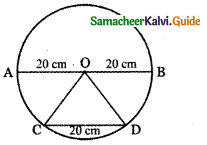
Given Diameter AB = 40 cm
∴ Radius r = 20 cm
Chord CD = 20 cm
O – Centre of the circle
OC = OD = radius = 20 cm.
∴ Triangle OCD is an equilateral triangle.
![]()
To find the length of the minor arc CD.
Let s = minor arc CD.
The arc CD subtends 60° at the centre.
θ = 60°
θ = 60° × \(\frac{\pi}{180}\) radians.
θ = \(\frac{\pi}{3}\) radians
We have s = rθ
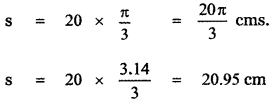
![]()
Question 5.
Find the degree measure of the angle subtended at the centre of the circle of radius 100 cm by an arc of length 22 cm.
Answer:
Given radius r = 100 cm.
Length of arc s = 22 cm.
Angle subtended by the arc at the centre = θ radians

Question 6.
What is the length of the arc intercepted by a central angle of measure 41° in a circle of radius of 10 feet?
Answer:
Central angle subtended by the arc θ = 41°
θ = 41 × \(\frac{\pi}{180}\) Radians
The radius of the circle r = 10 feet
Length of the arc = s
s = rθ
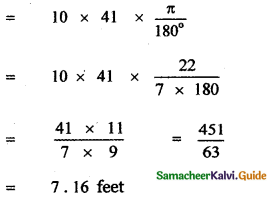
![]()
Question 7.
If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.
Answer:
Let r1 and r2 be the radii of the two circles and l be the length of the arc.
Given central angle θ1 = 60°

![]()
Question 8.
The perimeter of a certain sector of a circle is equal to the length of the arc of a semi-circle having the same radius. Express the angle of the sector in degrees, minutes, and seconds.
Answer:
Let OAB be the sector of a circle of radius r.
The angle of the sector is θ.

Perimeter of the sector = OA + arc AB + OB arc AB = rθ
∴ Perimeter of the sector = r + r θ + r
= 2r + rθ
= r(2 + θ) ———- (1)
Length of the arc of the semi – circle of radius
l = nπ ——– (2)
Given that perimeter the circular sector = Length of the arc of the semi circle of radius r
From equations (1) and (2), we have
r(2 + θ) = πr
2 + θ = π
θ = π – 2

![]()
Question 9.
An airplane propeller rotates 1000 times per minute. Find the number of degrees that a point on the edge of the propeller will rotate in 1 second.
Answer:
Given An airplane, the propeller rotates 1000 times per minute.
∴ A point on the edge of the propeller also rotates 1000 times in 1 minute.
∴ In 1 minute the point describes 1000 × 2π radians angle at the centre.
In 60 seconds the point describes 1000 × 2π radians angle.
∴ In 1 second the angle described = \(\frac{1000 \times 2 \pi}{60}\) radians
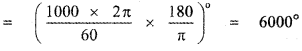
Question 10.
A train is moving on a circular track of a 1500 m radius at the rate of 66 km/hr. What angle will it turn in 20 seconds?
Answer:
Radius of the circular track r = 1500 m.
Speed of the train = 66 km/hr
Let θ be the angle made by the path of train at the centre in 20 seconds.
In 1 hr distance moved by train along the circular path = 66 km
In 60 × 60 seconds distance moved = 66 km
∴ In 20 seconds distance moved s = \(\frac{66}{60 \times 60}\) × 20

![]()
Question 11.
A circular metallic plate of radius 8 cm and thickness 6 nuns is melted and molded into a pie (a sector of the circle with thickness) of radius 16 cm and thickness 4 mm. Find the angle of the sector.
Answer:
Radius of the circular metallic plate r = 8 cm
Thickness of the plate h = 6 mm = \(\frac{6}{10}\)
Radius of the Pie l = 16 cm
Thickness of the Pie ( h) = 4mm = \(\frac{4}{10}\) cm
Given volume of the cylinder = Volume of the sector
