Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 2 Basic Algebra Ex 2.2 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.2
Question 1.
Solve for x
(i) |3 – x| < 7
Answer:
-7 < 3 – x < 7 3 – x > -7
-x > -7 -3 (= -10)
-x > -10 ⇒ x < 10
3 – x < 7
– x < 7 – 3 (= 4)
– x < 4x > -4 … .(2)
From (1) and (2)
⇒ x > -4 and x < 10
⇒ -4 < x < 10
![]()
![]()
(ii) |4x – 5| ≥ – 2
Answer:
|4x – 5| ≥ -2
(4x – 5) ≤ -(-2) or (4x – 5) ≥ -2
(4x – 5) ≤ 2 or (4x – 5) ≥ -2
4x ≤ 2 + 5 or 4x ≥ -2 + 5
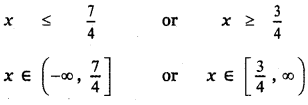
∴ x ∈ (-∞, ∞) = R
(iii) |3 – \(\frac{3}{4}\)x| ≤ \(\frac{1}{4}\)
Answer:
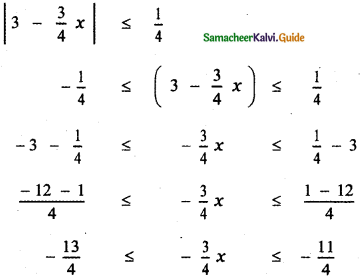
Multiplying by 4, we have
– 13 ≤ – 3x ≤ – 11 ——– (1)
We know that a < b ⇒ \(\frac{\mathrm{a}}{\mathrm{y}}\) > \(\frac{\mathrm{b}}{\mathrm{y}}\) when y < 0
Divide equation (1) by – 3, we have

![]()
(iv) |x| – 10 < – 3
Answer:
|x| – 10 < – 3
|x| < – 3 + 10
|x| < 7
– 7 < x < 7
∴ The solution set is (-7, 7)
![]()
Question 2.
Solve \(\frac{1}{|2 x-1|}\) < 6 and express the solution using the interval notation.
Answer:
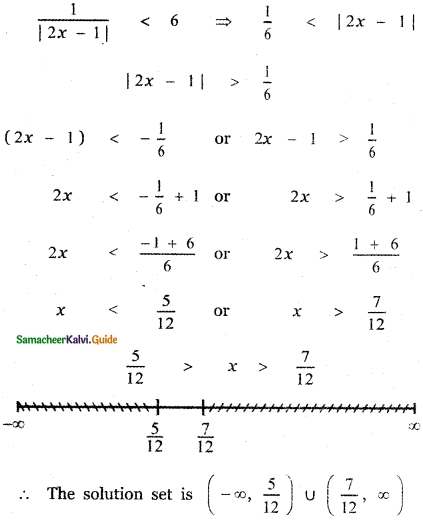
![]()
Question 3.
Solve – 3 |x| + 5 ≤ – 2 and graph the solution set in a number line.
Answer:
-3|x| + 5 ≤ – 2
⇒ -3 |x| ≤ – 2 – 5 (= -7)
-3|x| ≤ – 7 ⇒ 3 |x| ≥ 7
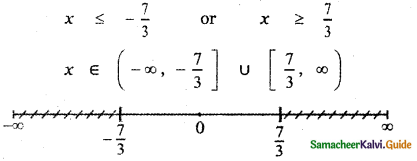
Question 4.
SoIve 2|x + 1| – 6 ≤ 7 and graph the solution set in a number line.
Answer:
Given 2|x + 1| – 6 ≤ 7
2|x + 1| ≤ 7 + 6
2|x + 1| ≤ 13
|x + 1| ≤ \(\frac{13}{2}\)
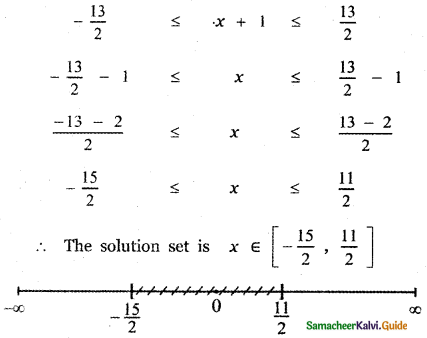
![]()
Question 5.
Solve \(\frac{1}{5}\) |10x – 2| < 1
Answer:
Given \(\frac{1}{5}\) |10x – 2| < 1
|10x – 2| < 5
-5 < (10x – 2) < 5
– 5 + 2 < 10x < 5 + 2
– 3 < 10x < 7
\(-\frac{3}{10}\) < x < \(\frac{7}{10}\)
∴ The solution set is x ∈ \(\left(-\frac{3}{10}, \frac{7}{10}\right)\)
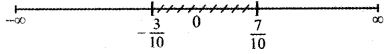
![]()
Question 6.
Solve |5x – 12| < – 2
Answer:
By the definition of modulus function. |5x – 12| always positive.
∴ |5x – 12| < -2 is not possible.
∴ Solution does not exist.