Samacheer Kalvi 11th Maths Guide Chapter 2 Basic Algebra Ex 2.12

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 2 Basic Algebra Ex 2.12 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.12

Question 1.
Let b > 0 and b ≠ 1. Express y = b^x in logarithmic form. Also, state the domain and range of the logarithmic function.
Answer:
Given y = b^x ⇒ log_by = x, x ∈ R with range (0, ∞) (-∞, ∞)

Question 2.
Compute log₉ 27 – log₂₇ 9
Answer:
log₉27 – log₂₇9 = log₉ 3³ – log₂₇ 3²
= 3 log₉ 3 – 2 log₂₇ 3 —— (1)
By change of base rule [log_b a = \(\frac{1}{\log _{a} b}\)]

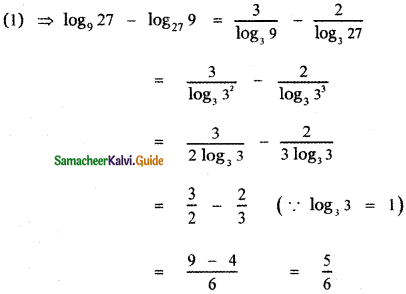
Question 3.
Solve log_ax + log₄x + log₂x = 11
Answer:

Question 4.
Solve log ₄ 2 ^8x = 2 ^log₂8
Answer:
Given log ₄ 2^8x = 2 ^log₂8
log ₄ 2^8x = 2^log₂23
log ₄ 2^8x = 2^{3 log₂2}
log ₄ 2^8x = 2³ = 8
2^8x = 4⁸
(2²)^4x = 4⁸
⇒ (4)^4x = 4⁸
⇒ 4x = 8
⇒ x = \(\frac { 8 }{ 4 }\) = 2

Question 5.
If a² + b² = 7ab, show that
log \(\left(\frac{a+b}{3}\right)\) = \(\frac{1}{2}\) (log a + log b)
Answer:
Given
a² + b² = 7ab
Adding both sides 2ab we get
a² + b² + 2ab = 7ab + 2ab
(a + b)² = 9ab

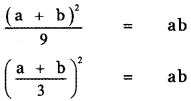
Taking square root on both sides

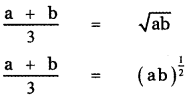
Taking logarithm on both sides

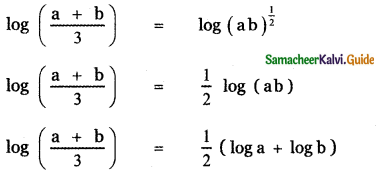
Question 6.
Prove that log \(\frac{\mathbf{a}^{2}}{\mathbf{b c}}\) + log \(\frac{\mathbf{b}^{2}}{\mathbf{c a}}\) + log \(\frac{c^{2}}{a b}\) = 0
Answer:

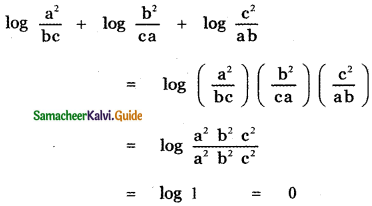
Question 7.
Prove that

Answer:

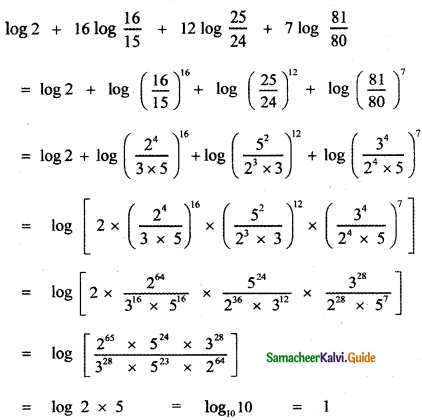
Question 8.
Prove that log_a² a + log_b² b + log_c² c = \(\frac{1}{8}\)
Answer:

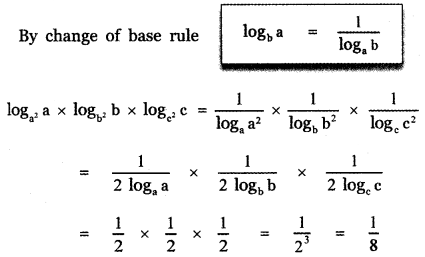
Question 9.
Prove log a + log a² + log a³ + ……… + log aⁿ = \(\frac{n(n+1)}{2}\) log a
Answer:
log a + log a² + log a³ + ……… + log aⁿ
= log a + 2 log a + 3 log a + ………….. + n log a
= log a (1 + 2 + 3 + ………….. + n)
= log a × \(\frac{n(n+1)}{2}\)
= \(\frac{n(n+1)}{2}\) log a

Question 10.
If 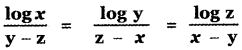, then prove that xyz = 1
Answer:
Let \(\frac{\log x}{y-z}\) = k
log x = k(y – z)
log x = ky – kz ——— (1)
Similarly log y = k(z – x) = kz – kx ——(2)
log z = k(x – y) = kx – ky ——- (3)
Adding (1), (2) and (3)
log x + log y + log z = ky – kz + kz – kx + kx – ky
log (xyz) = 0 = log 1
xyz = 1

Question 11.
Solve log₂x – 3 log_1/2x = 6
Answer:

Question 12.
Solve log_{5 – x} (x² – 6x + 65) = 2
Answer:
log_{5 – x}(x² – 6x + 65) = 2
⇒ x² – 6x + 65 = (5 – x)²
⇒ x² – 6x + 65 = 25 + x² – 10x
⇒ x² – 6x + 65 – 25 – x² + 10x = 0
⇒ 4x + 40 = 0
⇒ 4x = -40
⇒ x = -10