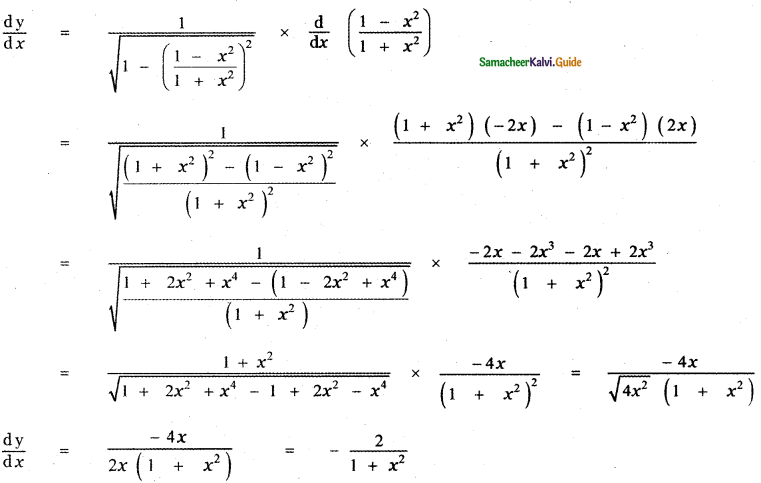Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 10 Differentiability and Methods of Differentiation Ex 10.3 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 10 Differentiability and Methods of Differentiation Ex 10.3
Differentiate the following:
Question 1.
y = (x2 + 4x + 6)5
Answer:
Let = u = x2 + 4x + 6
⇒ \(\frac{d u}{d x}\) = 2x + 4
Now y = u5 ⇒ \(\frac{d y}{d x}\) = 5u4
∴ \(\frac{d y}{d x}=\frac{d y}{d u} \times \frac{d u}{d x}\) = 5u4 (2x + 4)
= 5(x2 + 4x + 6)4 (2x + 4)
= 5 (2x + 4) (x2 + 4x + 6)4
![]()
Question 2.
y = tan 3x
Answer:
y = tan 3x
[ y = f(g(x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = sec2 3x . \(\frac{\mathrm{d}}{\mathrm{d} x}\) (3x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = sec23x × 3
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = 3 sec2 3x
Question 3.
y = cos (tan x)
Answer:
Put u = tan x
\(\frac{d u}{d x}\) = sec2x
Now y = cos u ⇒ \(\frac{d u}{d x}\) = -sin u
Now \(\frac{d y}{d x}=\frac{d y}{d u} \times \frac{d u}{d x}\)
= (-sin u) (sec2x)
= -sec2 (sin (tan x))
Question 4.
y = \(\sqrt[3]{1+x^{3}}\)
Answer:
y = \(\sqrt[3]{1+x^{3}}\)
y = (1 + x3)1/3
[ y = f(g(x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]
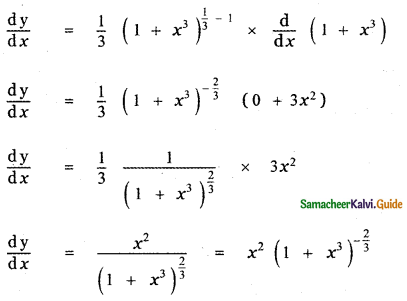
![]()
Question 5.
y = \(\mathrm{e}^{\sqrt{x}}\)
Answer:
y = \(\mathrm{e}^{\sqrt{x}}\)
y = \(e^{x^{\frac{1}{2}}}\)
[ y = f(g(x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]

Question 6.
y = sin (ex)
Answer:
y = sin (ex)
[ y = f(g(x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]
y = cos (ex) . \(\frac{\mathrm{d}}{\mathrm{d} x}\) (ex)
y = cos ((ex)) . ex
y = ex cos (ex)
Question 7.
F(x) = (x3 + 4x)7
Answer:
F(x) = (x3 + 4x)7
[ y = f(g(x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]
F’ (x) = 7 (x3 + 4x)7 – 1 \(\frac{\mathrm{d}}{\mathrm{d} x}\) (x3 + 4x)
= 7 (x3 + 4x)6 (3x2 + 4)
= 7 (3x2 + 4) (x3 + 4x)6
![]()
Question 8.
h (t) = \(\left(t-\frac{1}{t}\right)^{\frac{3}{2}}\)
Answer:
h (t) = \(\left(t-\frac{1}{t}\right)^{\frac{3}{2}}\)
[ y = f(g(x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]
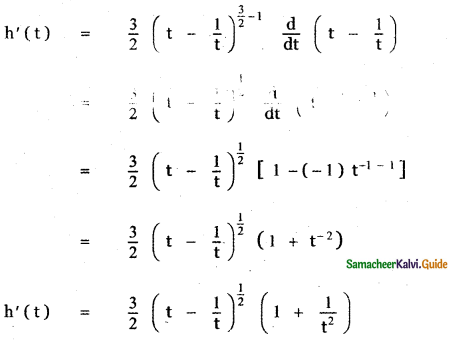
Question 9.
f(t) = \(\sqrt[3]{1+\tan t}\)
Answer:
f(t) = \(\sqrt[3]{1+\tan t}\)
f(t) = (1 + tan t)1/3
[ y = f(g(x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]

![]()
Question 10.
y = cos (a3 + x3)
Answer:
y = cos (a3 + x3)
[ y = f(g(x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = – sin (a3 + x3) \(\frac{\mathrm{d}}{\mathrm{d} x}\) (a3 + x3)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = – sin (a3 + x3) (0 + 3x2)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = – 3x2 sin (a3 + x3)
Question 11.
y = e-mx
Answer:
y = e-mx
[ y = f(g(x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = e-mx × \(\frac{\mathrm{d}}{\mathrm{d} x}\) (- mx)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = e-mx × – m
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = – m e-mx = – my
Question 12.
y = 4 sec 5x
Answer:
y = 4 sec 5x
[ y = f(g(x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = 4 × sec 5x × tan 5x \(\frac{\mathrm{d}}{\mathrm{d} x}\) (5x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = 4 sec 5x tan 5x × 5 × 1
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = 20 sec 5x tan 5x
![]()
Question 13.
y = (2x – 5)4 (8x2 – 5) – 3
Answer:
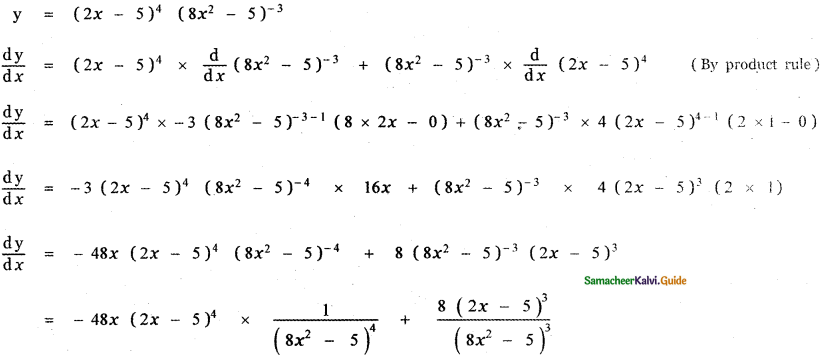

Question 14.
y = (x2 + 1) \(\sqrt[3]{x^{2}+2}\)
Answer:
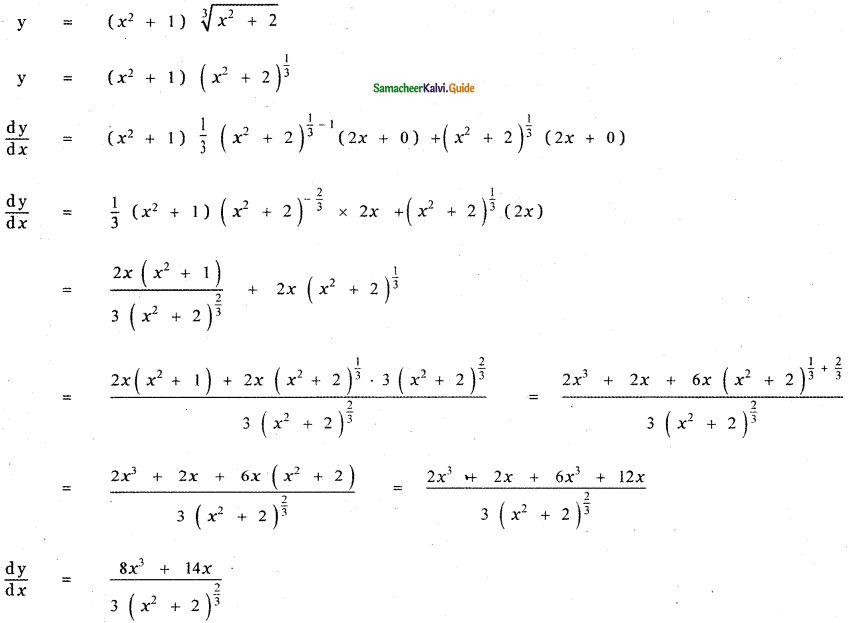
![]()
Question 15.
y = x e-x2
Answer:
y = xe-x2
y = uv where u = x and v = e-x2
Now u’ = 1 and v’ = e-x2 (-2x)
v’ = – 2xe-x2
Now y = uv ⇒ y’ = uv’ + vu’
(i.e.) \(\frac{d y}{d x}\) = x[-2xe-x2] + e-x2 (1)
= e-x2 (1 – 2x2)
Question 16.
s(t) = \(\sqrt[4]{\frac{t^{3}+1}{t^{3}-1}}\)
Answer:
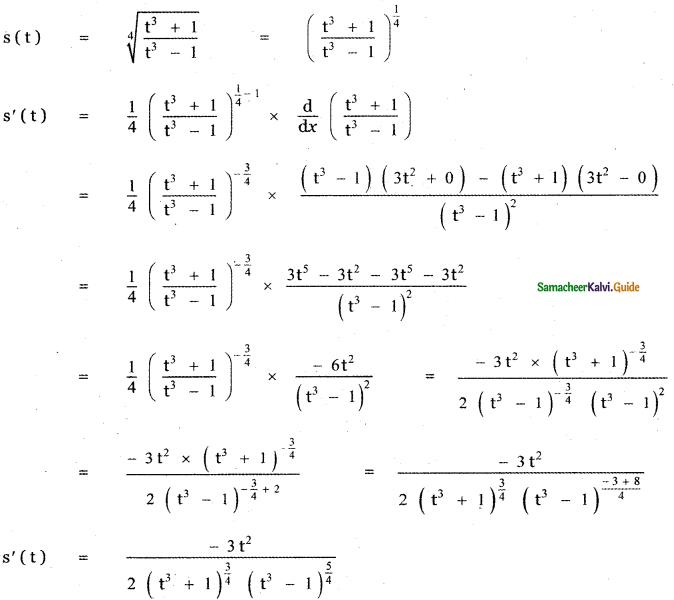
Question 17.
f(x) = \(\frac{x}{\sqrt{7-3 x}}\)
Answer:
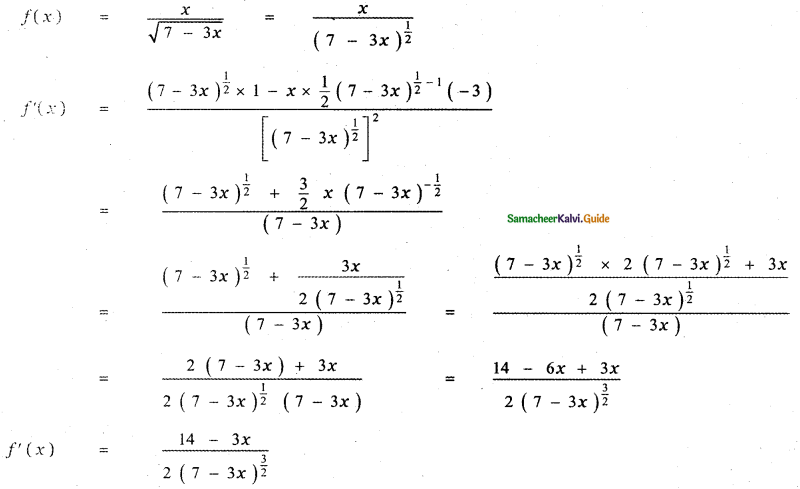
![]()
Question 18.
y = tan (cos x)
Answer:
y = tan (cos x)
[ y = f(g(x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = sec2 (cos x) × \(\frac{\mathrm{d}}{\mathrm{d} x}\) (cos x)
= sec2 (cos x) × – sin x
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = -sin x . sec2 (cos x)
Question 19.
y = \(\frac{\sin ^{2} x}{\cos x}\)
Answer:
y = \(\frac{\sin ^{2} x}{\cos x}\)
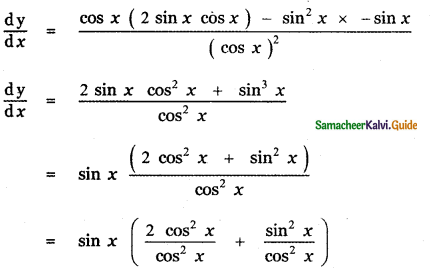
= sin x (2 + tan2x)
= sin x (1 + 1 + tan2x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = sin x (1 + sec2 x)
Question 20.
y = \(5^{\frac{-1}{x}}\)
Answer:
y = \(5^{\frac{-1}{x}}\)
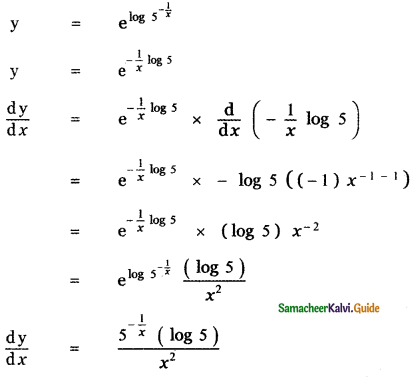
![]()
Question 21.
y = \(\sqrt{1+2 \tan x}\)
Answer:

Question 22.
y = sin3x + cos3x
Answer:
y = sin3x + cos3x
Here u = sin3 x = (sin x)3
⇒ \(\frac{d u}{d x}\) = 3 (sin x)2 (cos x)
= 3sin2x cos x
v = cos3x = (cos x)3
⇒ \(\frac{d v}{d x}\) = 3 (cos x)2 (-sin x) = -3 sin x cos2x
Now y = u + v ⇒ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\)
= 3 sin2x cos x – 3sin x cos2x
= 3 sin x cos x (sin x – cos x)
Question 23.
y = sin2 (cos kx)
Answer:
y = sin2 (cos kx)
y = f(g(x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = 2 sin (cos kx) × cos (cos kx) × -sin kx × k × 1
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = sin (2 cos kx) × -k sin kx
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = -k sin kx . sin (2 cos kx)
![]()
Question 24.
y = (1 + cos2)6
Answer:
y = (1 + cos2)6
y = f(g(x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = 6(1 + cos2x)6-1 (0 + 2 cos x × -sin x)
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = 6(1 + cos2x)5 × – 2 sin x cos x
\(\frac{\mathrm{dy}}{\mathrm{d} x}\) = -6 sin 2x (1 + cos2)5
Question 25.
y = \(\frac{e^{3 x}}{1+e^{x}}\)
Answer:
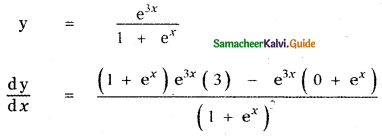

Question 26.
y = \(\sqrt{x+\sqrt{x}}\)
Answer:
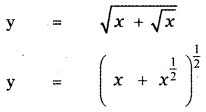
[y = f(g(x))
\(\frac{\mathrm{d} \mathrm{y}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]
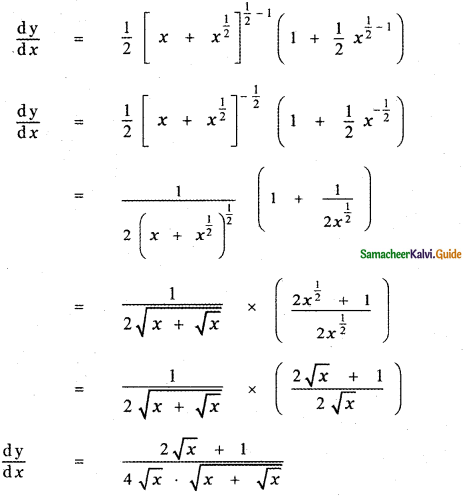
![]()
Question 27.
y = ex cos x
Answer:
y = ex cos x
\(\frac{\mathrm{d} \mathrm{y}}{\mathrm{d} x}\) = ex cos x (x – sinx + cos x . 1)
\(\frac{\mathrm{d} \mathrm{y}}{\mathrm{d} x}\) = ex cos x (cos x – x sin x)
Question 28.
y = \(\sqrt{x+\sqrt{x+\sqrt{x}}}\)
Answer:

[y = f(g(x))
\(\frac{\mathrm{d} \mathrm{y}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]
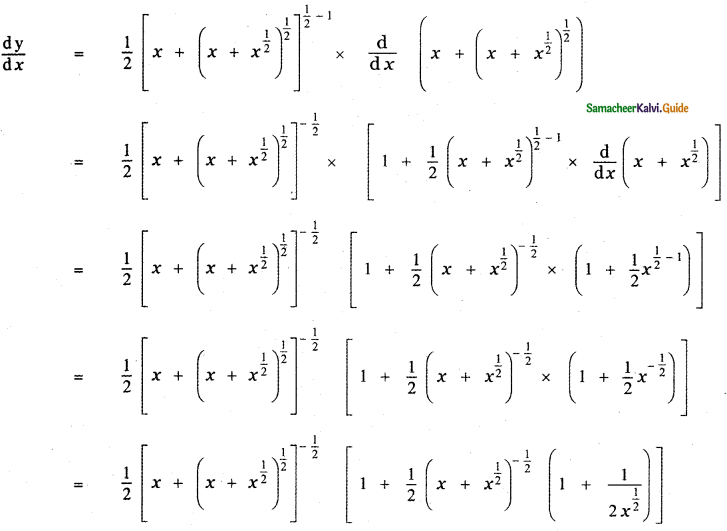
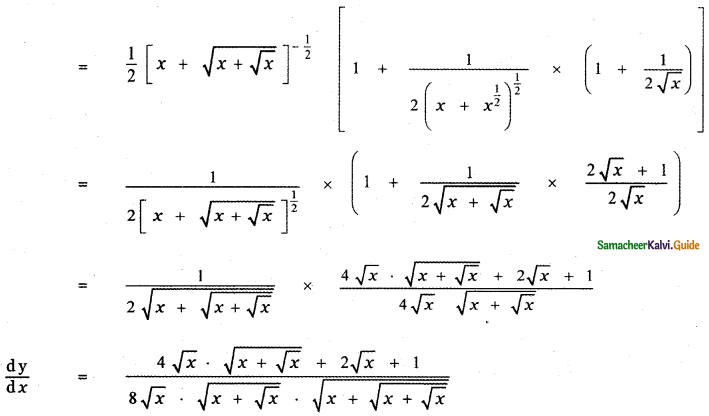
Question 29.
y = sin (tan (\(\sqrt{\sin x}\)))
Answer:
y = sin (tan (\(\sqrt{\sin x}\)))
y = f(g(x))
\(\frac{\mathrm{d} \mathrm{y}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]
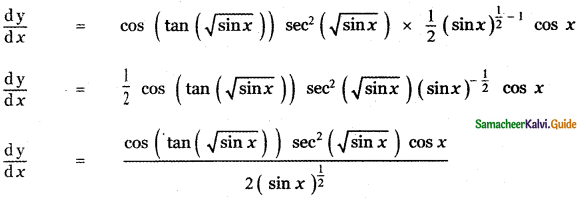
![]()
Question 30.
y = sin-1\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
Answer:
y = sin-1\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
[y = f(g(x))
\(\frac{\mathrm{d} \mathrm{y}}{\mathrm{d} x}\) = f'(g(x)) . g'(x)]