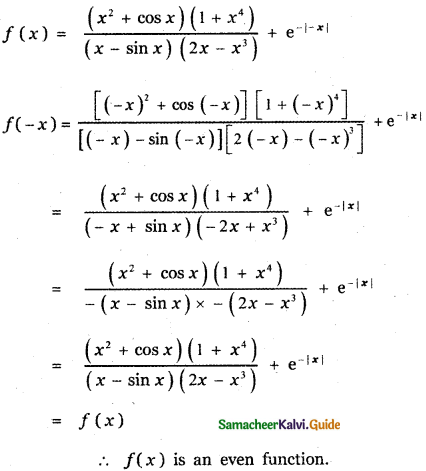Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 1 Sets, Relations and Functions Ex 1.5 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets, Relations and Functions Ex 1.5
Choose the correct or the most suitable answer.
Question 1.
If A = {(x,y): y = ex, x ∈ R} and B = {(x, y): y = e-x, x ∈ R},then n(A ∩ B) is
(1) Infinity
(2) 0
(3) 1
(4) 2
Answer:
(3) 1
![]()
Explaination:
Given
A = {(x,y): y = ex, x ∈ R}
B = {(x,y): y = e-x, x ∈ R}
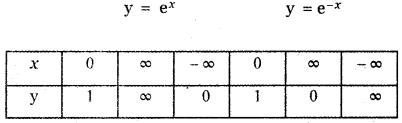
Consider the curve y = ex
When x = 0 ⇒ y = e-0 = 1
When x = ∞ ⇒ y = e-∞ = ∞
When x = -∞ ⇒ y = e∞ = 0
Consider the curve y = e-x.
When x = 0 ⇒ y = e-0 = 1
When x = ∞ ⇒ y = e-∞ = 0
When x = -∞ ⇒ y = e∞ = ∞
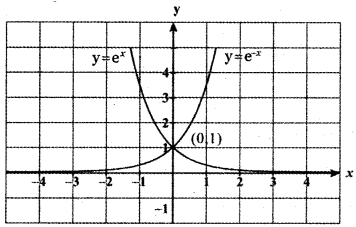
(0, 1) is the only point common to y = e<sup.x and y = e-x
∴ A ∩ B = {(0,1)} ⇒ n (A ∩ B ) = 1
![]()
Question 2.
If A = { ( x, y): y = sin x, x ∈ R } and B = { ( x, y): y = cos x, x ∈ R} then A ∩ B contains
(1) no element
(2) infinitely many elements
(3) only one element
(4) cannot be determined
Answer:
(2) infinitely many elements
Explaination:
Given A = { (x, y): y = sin x, x ∈ R}
B = {(x, y): y = cos x, x ∈ R }
Consider the equations y = sin x and y = cos x
sin x = cos x ⇒ \(\frac{\sin x}{\cos x}\) = 1
tan x = 1 ⇒ x = nπ + \(\) for n ∈ z
There are infinite number of common points for the sets A and B
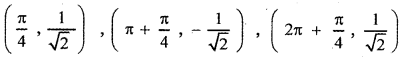
Question 3.
The relation R defined on a set A = {0, -1, 1, 2} by x R y if |x2 + y2| ≤ 2,
then which one of the following is true.
(1) R = {(0,0), (0,-1), (0,1), (-1,0), (-1,1), (1,2), (1,0)}
(2) R-1 = {(0, 0), (0, -1), (0, 1), (-1, 0), (1, 0)}
(3) Domain of R is {0,- 1, 1, 2}
(4) Range of R is {0, -1, 1}
Answer:
(4) Range of R is {0, -1, 1}
Explaination:
A= {0, -1, 1, 2}
|x2 + y2| ≤ 2
The values of x and y can be 0, -1 or 1
So range = {0, -1, 1}
![]()
Question 4.
If f(x) = |x – 2 | + |x + 2| x ∈ R then
(1) 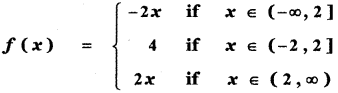
(2) 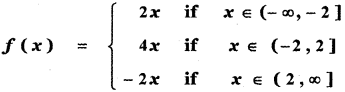
(3) 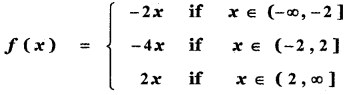
(4) 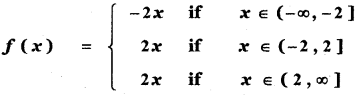
Answer:
(1) 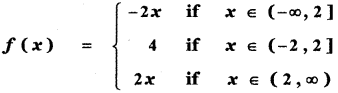
Explaination:
f(x) = |x – 2| + |x + 2|, x ∈ R
Divide the Real line into three intervals
In the interval (2, ∞), both the factors x – 2 and x + 2 are positive.
∴ f(x) = x – 2 + x + 2 = 2x
f(x) = 2x for all x ∈ (2, ∞)

In the interval (- ∞, – 2 ] both the factors x – 2 and x + 2 are negative.
∴ f(x) = – (x – 2) – (x + 2)
= – x + 2 – x – 2 = – 2x
∴ f(x) = – 2x for all x ∈ (- ∞,- 2]
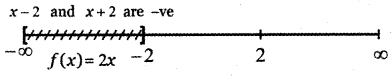
In the interval (—2, 2], the factor x – 2 is negative and the factor x + 2 is positive.
∴ f(x) = – (x – 2) + (x + 2)
f(x) = – x + 2 + x + 2 = 4
Thus f(x) = 4 for all x ∈ (- 2, – 2]
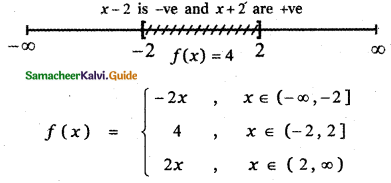
![]()
Question 5.
Let R be the set of all real numbers. Consider the following subsets of the plane R × R:
S = { (x, y): y = x + 1 and 0 < x < 27 and
T = {(x, y): x – y is an integer} Then which of the following is true?
(1) T is an equivalence relation but S Is not an equivalence relation
(2) Neither S nor T is an equivalence relation
(3) Both S and T are equivalence relation
(4) S is an equivalence relation but T is not an equivalence relation.
Answer:
(1) T is an equivalence relation but S Is not an equivalence relation
Explanation:
(0, 1), (1, 2) it is not an equivalence relation
T is an equivalence relation
![]()
Question 6.
Let A and B be subsets of the universal set N, the set of natural numbers. Then A’ ∪ [(A ∩ B) ∪ B’] is
(1) A
(2) A’
(3) B
(4) N
Answer:
(4) N
Explaination:
Let N = {1, 2, 3, ……….. 10}
A = { 1, 2, 3, 4, 5 }
B = {6, 7, 8, 9, 10}
A’ = {6, 7, 8, 9, 10 }
B’ = { 1 , 2, 3, 4, 5 }
A ∪ B = {1, 2, 3, 4, 5} ∪ {6, 7, 8, 9, 10}
A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(A ∪ B) ∩ B’ = {1,2, 3, 4, 5, 6,7, 8, 9,10} ∩ { 1, 2, 3, 4 , 5 }
(A ∪ B) ∩ B’= {1,2, 3,4, 5}
A’ ∪ [(A ∪ B ) ∩ B’] = { 6, 7, 8, 9 , 10 } ∪ {1, 2, 3, 4, 5 }
= {1, 2, 3, 4,5, 6, 7, 8, 9, 10}
A’ ∪ [(A ∪ B) ∩ B’] = N
![]()
Question 7.
The number of students who take both the subjects Mathematics and Chemistry is 70. This represents 10% of the enrollment in Mathematics and 14% of the enrollment in Chemistry. The number of students takes atleast one of these two subjects, is
(1) 1120
(2) 1130
(3) 1100
(4) Insufficient data
Answer:
(2) 1130
Explanation:
n(M ∪ C) = n(M) + n(C) – n(M ∩ C)
= 700 + 500 – 70
= 1130
![]()
Question 8.
If n[ (A × B) n (A × C) ] = 8 and n(B ∩ C) = 2 then n(A) is
(1) 6
(2) 4
(3) 8
(4) 16
Answer:
(2) 4
Explaination:
Given n[(A × B) n (A × C)] = 8
n(B ∩ C) = 2
n[(A × B) ∩ (A × C)] = 8
A × (B ∩ C) = (A × B) ∩ (A × C) ]
⇒ n [A × (B ∩ C)] = 8
⇒ n(A) . n (B ∩ C) = 8
⇒ n(A). 2 = 8
⇒ n(A) = \(\frac{8}{2}\) = 4
Question 9.
If n(A) = 2 and n(B ∪ C) = 3,then n[(A × B) ∪ (A × C)] is
(1) 23
(2) 32
(3) 6
(4) 5
Answer:
(3) 6
Explaination:
n[(A × B) ∪ (A × C)] = n[ A × (B ∪ C)] = n(A) × n(B ∪ C)
= 2 × 3
= 6
![]()
Question 10.
If two sets A and B have 17 elements in common, then the number of elements common to the set A × B and B × A is
(1) 217
(2) 172
(3) 34
(4) Insufficient data
Answer:
(2) 172
Explanation:
If two sets A and B have 17 elements in common, then the number of elements common to the set A × B
and B × A is 172
Question 11.
For non-empty sets A and B, if A ⊂ B then (A × B) ∩ (B × A) is equal to
(1) A ∩ B
(2) A × A
(3) B × B
(4) None of these
Answer:
(2) A × A
Explanation:
When A ⊂ B, (A × B) ∩ (B × A) = A × A
![]()
Question 12.
The number of relations on a set containing 3 elements is
(1) 9
(2) 81
(3) 512
(4) 1024
Answer:
(3) 512
Explanation:
The number of relations on a set containing n elements is 2n2. Here n = 3
∴ Required number = 232 = 29
= 512
Question 13.
Let R be the universal relation on a set X with more than one element. Then R is
(1) not reflexive
(2) not symmetric
(3) transitive
(4) none of the above
Answer:
(3) transitive
Explanation:
Given R is a universal relation on the set X.
The universal relation is always an equivalence relation.
R is reflexive, symmetric, and transitive.
![]()
Question 14.
Let X = { 1, 2, 3, 4 } and R = { ( 1, 1 ), (1, 2), (1, 3), (2, 2), (3, 3), (2, 1), (3, 1), (1, 4), ( 4, 1) } . Then R is
(1) Reflexive
(2) Symmetric
(3) Transitive
(4) Equivalence
Answer:
(2) Symmetric
Explanation:
(4, 4} ∉ R ⇒ R is not reflexive
(1, 4), (4, 1) ∈ R ⇒ R is symmetric
(1, 4), (4, 1) ∈ R but (4, 4) ∉ R
So R is not transitive
Question 15.
The range of the function \(\frac{1}{1-2 \sin x}\) is
(1) (- ∞, – 1) ∪ (\(\frac{1}{3}\), ∞)
(2) (-1, \(\frac{1}{3}\))
(3) [-1, \(\frac{1}{3}\)]
(4) (- ∞, – 1] ∪ [\(\frac{1}{3}\), ∞)
Answer:
(4) (- ∞, – 1] ∪ [\(\frac{1}{3}\), ∞)
Explaination:
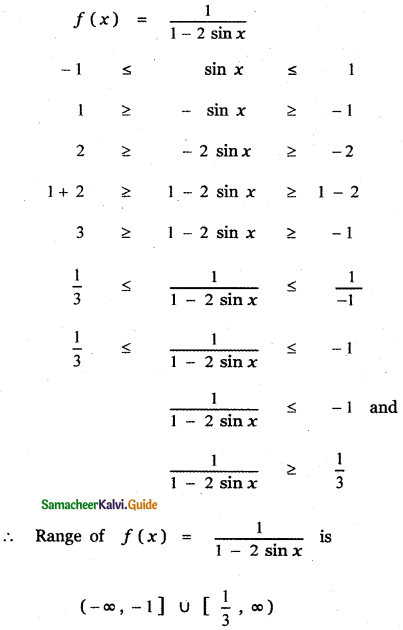
![]()
Question 16.
The range of the function
f(x) = |[x] – x|, x ∈ R is
(1) [0, 1]
(2) [0, ∞)
(3) [0, 1)
(4) (0, 1)
Answer:
(3) [0, 1)
Explaination:
f(x) = |[x] – x|
When x = 1 ,
we have [x] = [1] = 1
f(1) = |1 – 1| = o
When x = 1.5
we have [x} = [1.5] = 1
f(1.5) = |1 – 1.5| = |- 0.5| = 0.5
When x = 2.5
we have [x] = [2.5] = 2
f (2.5) = |2 – 2.5| = |- 0.5| = 0.5
When x = – 2.5
we have [x] = [- 2.5] = – 3
f (-2.5) = |- 3 – (-2.5| = |- 3 + 0.5| = |- 0.5| = 0.5
∴ Range of f(x) = |[x] – x| is [0, 1)
![]()
Question 17.
The rule f(x) = x2 is a bijection if the domain and the co – domain are given by
(1) R, R
(2) R,(0, ∞)
(3) (0, ∞)R
(4) [0, ∞), [0, ∞)
Answer:
(4) [0, ∞), [0, ∞)
Explaination:
Let x ∈ R, then x can be negative or zero or positive.
Given f(x) = x2
The image of x under f is always positive since x2 is positive for x = 1 and x = – 1 ∈ R
f(1) = 12 = 1
f(-1) = (-1)2 = 1
∴ 1, – 1 have the same image
∴ f is not one – one if the domain is R.
Suppose the domain is [0, ∞) then f is one – one and onto.
Domain = [0, ∞)
Co-domain = [0, ∞)
![]()
Question 18.
The number of constant functions from a set containing m elements to a set containing n elements is
(1) mn
(2) m
(3) n
(4) m + n
Answer:
(3) n
Explanation:
Let A be a set having m elements and B be a set having n elements.
When all the elements of A mapped onto the first element of B we get the first constant function. When all the elements of A mapped onto the second element of B we get the second constant function.
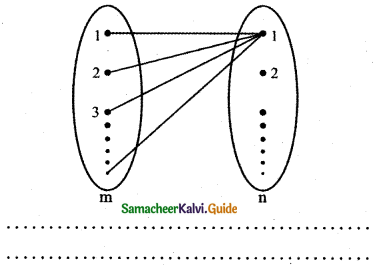
When all the elements of A mapped on to the nth element of B, we get the nth constant function.
∴ The number of constant functions possible is n.
![]()
Question 19.
The function f:[0, 2π] → [- 1, 1] defined by f(x) = sin x is
(1) one to one
(2) onto
(3) bijection
(4) cannot be defined
Answer:
(2) onto
Explaination:
f : [0, 2π] → [- 1, 1]
Defined by f (x) = sin x
f(0) = sin 0 = 0
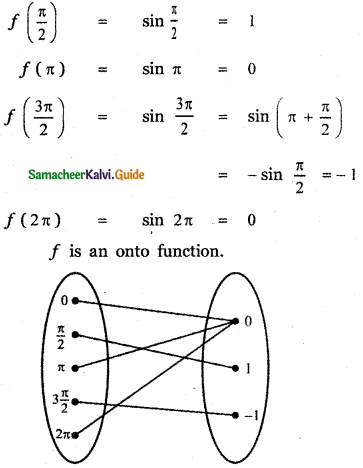
![]()
Question 20.
If the function f : [-3, 3] → S defined by f(x ) = x2 is onto, then S is
(1) [-9, 9]
(2) R
(3) [-3, 3]
(4) [0, 9]
Answer:
(4) [0, 9]
Explaination:
f: [-3, 3] → S defined by f(x) = x2
f(-3) = (-3)2 = 9
f(0) = 02 = o
f(3) = 32 = 9
∴ S = [0, 9]
Question 21.
Let X = {1, 2, 3, 4}, Y = { a, b , c, d } and f = {(1, a), (4, b), (2, c), (3, d), (2, d)}. Then f is
(1) an one – to – one function
(2) an onto function
(3) a function which is not one to one
(4) not a function
Answer:
(4) not a function
Explaination:
X = {1, 2, 3, 4}, Y = {a, b, c, d>
f = {(1, a), (4, b), (2, c), (3, d), (2, d)}
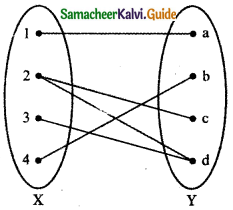
f is not a function since 2 ∈ X has two images c and d.
![]()
Question 22.
The inverse of
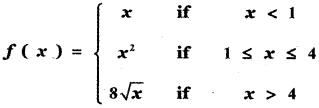
(1) 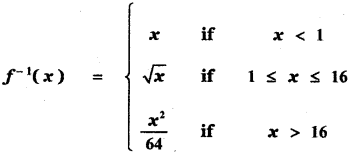
(2) 
(3) 
(4) 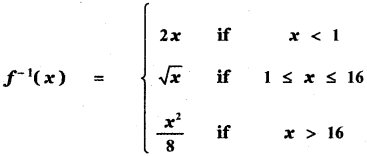
Answer:
(1) 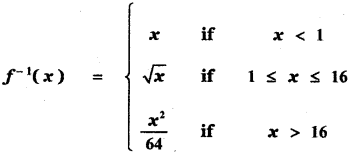
![]()
Explaination:
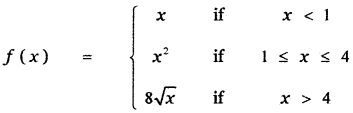
Let f(x) = x if x < 1 —— (1)
Put y = x then
(1) ⇒ f(x) = y
⇒ x = f-1(y) if y < 1
⇒ y = f-1(y) if y < 1
⇒ f-1(x) = x if x < 1
Let f(x) = x2 if 1 ≤ x ≤ 4 —– (2)
Put y = x2 ⇒ x = √y, if 1 ≤ y ≤ 16
then (2) ⇒ f(x) = y
⇒ x = f-1(y) if 1 ≤ y ≤ 16
⇒ √(y) = f-1(y) if 1 ≤ y ≤ 16
⇒ √x = f-1(y) if 1 ≤ x ≤ 16
Let f(x) = 8√x if x > 4 ———– (3)
Put y = 8√x ⇒ y2 = 64 x
⇒ x = \(\frac{y^{2}}{64}\) if y>16
then (3) ⇒ f(x) = y
⇒ x = f-1(y) if y > 16
⇒ √y = f-1(y) if y > 16
⇒ \(\frac{y^{2}}{64}\) = f-1(x) if x > 16
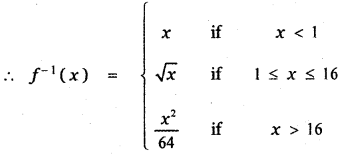
![]()
Question 23.
Let f: R → R be defined by f(x) = 1 – |x|. Then the range of f is
(1) R
(2) (1, ∞)
(3) (-1, ∞)
(4) (- ∞, 1)
Answer:
(4) (- ∞, 1)
Explaination:
f: R ➝ R defined by
f(x) = 1 – |x|
For example,
f(1) = 1 – 1 = 0
f(8) = 1 – 8 = -1
f(-9) = 1 – 9 = -8
f(-0.2) = 1 – 0.2 = 0.8
so range = (-∞, 1]
Question 24.
The function f : R → R be defined by f(x) = sin x + cos x is
(1) an odd function
(2) neither an odd function nor an even function
(3) an even function
(4) both odd function and even function
Answer:
(2) neither an odd function nor an even function
Explaination:
f : R → R is defined by f(x) = sin x + cos x
f(-x) = sin (-x) + cos (-x) = -sin x + cos x ≠ f (x)
If f(-x) = -f(x) then f(x) is an odd function.
If f(-x) = f(x) then f(x) is an even function.
∴ f (x) is neither odd function nor an even function.
![]()
Question 25.
The function f : R → R be defined by
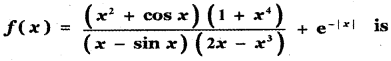
(1) an odd function
(2) neither an odd function nor an even function
(3) an even function
(4) both odd function and even function.
Answer:
(3) an even function
Explanation: