Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Chemistry Guide Pdf Chapter 7 Thermodynamics Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Chemistry Solutions Chapter 7 Thermodynamics
11th Chemistry Guide Thermodynamics Text Book Back Questions and Answers
Textual Questions:
I. Choose the best answer:
Question 1.
The amount of heat exchanged with the surrounding at constant temperature and pressure is given by the quantity
(a) ∆E
(b) ∆H
(c) ∆S
(d) ∆G
Answer:
(b) ∆H
Question 2.
All the naturally occurring processes proceed spontaneously in a direction which leads to
(a) decrease in entropy
(b) increase in enthalpy
(c) increase in free energy
(d) decrease in free energy
Answer:
(d) decrease in free energy
Question 3.
In an adiabatic process, which of the following is true?
(a) q = w
(b) q = 0
(c) ∆E = q
(d) P∆V = 0
Answer:
(b) q = 0
Question 4.
In a reversible process, the change in entropy of the universe is
(a) > 0
(b) ≥ 0
(c) <0
(d) = 0
Answer:
(d) = 0
Question 5.
In an adiabatic expansionof an ideal gas
(a) w = – ∆U
(b) w = ∆U + ∆H
(c) ∆U = 0
(d) w = 0
Answer:
(a) w = – ∆U
![]()
Question 6.
The intensive property among the quantities below is
(a) mass
(b) volume
(c) enthalpy
(d) mass/volume
Answer:
(d) mass/volume
Question 7.
An ideal gas expands from the volume of 1 × 10-3 m3 to 1 × 10-2 m3 at 300 K against a constant pressure at 1 × 105 Nm-2. The work done is
(a) -900 J
(b) 900 kJ
(c) 270 kJ
(d) – 900 kJ
Answer:
(a) -900 J
Question 8.
Heat of combustion is always
(a) positive
(b) negative
(c) zero
(d) either positive or negative
Answer:
(b) negative
Question 9.
The heat of formation of CO and CO2 are -26.4 kCal and -94 kCal, respectively. Heat of combustion of carbon monoxide will be
(a) + 26.4 kcal
(b) – 67.6 kcal
(c) – 120.6 kcal
(d) + 52.8 kcal
Answer:
(b) – 67.6 kcal
Question 10.
C(diamond) → C(graphite), ∆H = -ve, this indicates that
(a) graphite is more stable than diamond
(b) graphite has more energy than diamond
(c) both are equally stable
(d) stability cannot be predicted
Answer:
(a) graphite is more stable than diamond
![]()
Question 11.
The enthalpies of formation of Al2O3 and Cr2O3 are – 1596 kJ and – 1134 kJ, respectively.
∆H for the reaction 2Al + Cr2O3 → 2Cr + Al2O3 is
(a) – 1365 kJ
(b) 2730 kJ
(c) – 2730 kJ
(d) -462 kJ
Answer:
(d) -462 kJ
Question 12.
Which of the following is not a thermodynamic function?
(a) internal energy
(b) enthalpy
(c) entropy
(d) frictional energy
Answer:
(d) frictional energy
Question 13.
If one mole of ammonia and one mole of hydrogen chloride are mixed in a closed container to form ammonium chloride gas, then
(a) ∆H > ∆U
(b) ∆H – ∆U=0
(c) ∆H + ∆U=0
(d) ∆H < ∆U
Answer:
(d) ∆H < ∆U
Question 14.
Change in internal energy, when 4 kJ of work is done on the system and 1 kJ of heat is given out by the system is
(a) +1 kJ
(b) -5 kJ
(c) +3 kJ
(d) -3 kJ
Answer:
(c) +3 kJ
Question 15.
The work done by the liberated gas when 55.85 g of iron (molar mass 55.85 g mol-1) reacts with hydrochloric acid in an open beaker at 25°C
(a) – 2.48 kJ
(b) – 2.22 kJ
(c) + 2.22 kJ
(d) + 2.48 kJ
Answer:
(a) – 2.48 kJ
![]()
Question 16.
The value of ∆H for cooling 2 moles of an ideal monatomic gas from 1250°C to 250°C at constant pressure will be [given Cp = \(\frac{5}{2}\)R]
(a) – 250 R
(b) – 500 R
(c) 500 R
(d) + 250 R
Answer:
(b) – 500 R
Question 17.
Given that C(g) + O2(g) → CO2(g) ∆H° = – a kJ;
2 CO(g) + O2(g) → 2CO2(g) ∆H° = -b kJ; Calculate the ∆H° for the reaction C(g) + ½O2(g) → CO(g)
(a) \(\frac{b+2 a}{2}\)
(b) 2a – b
(c) \(\frac{2 a-b}{2}\)
(d) \(\frac{b-2 a}{2}\)
Answer:
(d) \(\frac{b-2 a}{2}\)
Question 18.
When 15.68 litres of a gas mixture of methane and propane are fully combusted at 0° C and 1 atmosphere, 32 litres of oxygen at the same temperature and pressure are consumed. The amount of heat of released from this combustion in kJ is (∆HC(CH4)) = – 890 kJ mol and ∆HC(C3H8) = – 2220 kJ mol-1)
(a) -889 kJ
(b) -1390 kJ
(c) -3180 kJ
(d) -632.68 kJ
Answer:
(d) -632.68 kJ
Question 19.
The bond dissociation energy of methane and ethane are 360 kJ mol-1 and 620 kJ mol-1 respectively. Then, the bond dissociation energy of C-C bond is
(a) 170 kJ mol-1
(b) 50 kJ mol-1
(c) 80 kJ mol-1
(d) 220 kJ mol-1
Answer:
(c) 80 kJ mol-1
Question 20.
The correct thermodynamic conditions for the spontaneous reaction at all temperature is
(a) ∆H < 0 and ∆S > 0
(b) ∆H < 0 and ∆S < 0
(c) ∆H > 0 and ∆S = 0
(d) ∆H > 0 and ∆S > 0
Answer:
(a) ∆H < 0 and ∆S > 0
![]()
Question 21.
The temperature of the system, decreases in an
(a) Isothermal expansion
(b) Isothermal Compression
(c) adiabatic expansion
(d) adiabatic compression
Answer:
(c) adiabatic expansion
Question 22.
In an isothermal reversible compression of an ideal gas the sign of q, ∆S and w are respectively
(a) +, -, –
(b) -, +, –
(c) +, -, +
(d) -, -, +
Answer:
(d) -, -, +
Question 23.
Molar heat of vapourisation of a liquid is 4.8 kJ mol-1 If the entropy change is 16 J mol-1 K-1. the boiling point of the liquid is
(a) 323 K
(b) 27°C
(c) 164 K
(d) 0.3 K
Answer:
(b) 27°C
Question 24.
∆S is expected to be maximum for the reaction
(a) Ca(S) + 1/2 O2(g) → CaO(S)
(b) C(S) + O2(g) → CO2(g)
(c) N2(g) + O2(g) → 2NO(g)
(d) CaCO3(S) → CaO(S) + CO2(g)
Answer:
(d) CaCO3(S) → CaO(S) + CO2(g)
Question 25.
The values of ∆H and ∆S for a reaction are respectively 30 kJ mol-1 and 100 JK-1 mol-1. Then the temperature above which the reaction will become spontaneous is
(a) 300 K
(b) 30 K
(c) 100 K
(d) 20°C
Answer:
(a) 300 K
![]()
II. Write brief answers to the following questions:
Question 26.
State the first law of thermodynamics.
Answer:
The first law of thermodynamics, known as the law of conservation of energy, states that the total energy of an isolated system remains constant though it may change from one foim to another.
The mathematical statement of the First Law as:
∆U = q + w
where q – the amount of heat supplied to the system; w – work done on the system.
Question 27.
Define Hess’s law of constant heat summation.
Answer:
The heat changes in chemical reactions are equal to the difference in internal energy (∆U) or heat content (∆H) of the products and reactants, depending upon whether the reaction is studied at constant volume or constant pressure. Since ∆U and ∆H are functions of the state of the system, the heat evolved or absorbed in a given reaction depends only on the initial state and final state of the system and not on the path or the steps by which the change takes place.
Question 28.
Explain intensive properties with two examples.
Answer:
The property that is independent of the mass or the size of the system is called an intensive property. Refractive index, Surface tension, density, temperature, Boiling point, Freezing point, molar volume.
Question 29.
Define the following terms:
(a) isothermal process
(b) adiabatic process
(c) isobaric process
(d) isochoric process
Answer:
a. An isothermal process is defined as one in which the temperature of the system remains constant, during the change from its initial to final state. The system exchanges heat with its surrounding and the temperature of the system remains constant. For an isothermal process dT = 0.
b. An adiabatic process is defined as one in which there is no exchange of heat (q) between the system and surrounding during the process. Those processes in which no heat can flow into or out of the system are called adiabatic processes.
c. An isobaric process is defined as one in which the pressure of the system remains constant
during its change from the initial to final state.
For an isobaric process dP = 0.
d. An isochoric process is defined as the one in which the volume of system remains constant during its change from initial to final state. Combustion of a fuel in a bomb calorimeter is an example of an isochoric process.
For an isochoric process, dV= 0.
Question 30.
What is the usual definition of entropy? What is the unit of entropy?
Answer:
Entropy is a measure of the molecular disorder (randomness) of a system.
The thermodynamic definition of entropy is concerned with the change in entropy that occurs as a result of a process.
It is defined as, dS = dqrev /T
![]()
Question 31.
Predict the feasibility of a reaction when
(i) both ∆H and ∆S positive
(ii) both ∆H and ∆S negative
(iii) ∆H decreases but ∆S increases
Answer:
(i) ∆Hr = + ve, ∆S = + ve; non-spontaneous at low temperature spontaneous at high temperature
(ii) ∆Hr = – ve, ∆S = – ve; spontaneous at low temperature non-spontaneous at high temperature
(iii) ∆H decreases but ∆S increases = Spontaneous at all temperature.
Question 32.
Define is Gibb’s free energy.
Answer:
G is expressed as G = H – TS, free energy change of a process is given by the relation
∆G = ∆H – T∆S.
Question 33.
Define enthalpy of combustion.
Answer:
The heat of combustion of a substance is defined as “The change in enthalpy of a system when one mole of the substance is completely burnt in excess of air or oxygen”. It is denoted by ∆HC.
Question 34.
Define molar heat capacity. Give its unit.
Answer:
The heat capacity for 1 mole of substance, is called molar heat capacity (cm). It is defined as “The amount of heat absorbed by one mole of the substance to raise its temperature by 1 kelvin”.
The SI unit of molar heat capacity is JK-1 mol-1
Question 35.
Define the calorific value of food. What is the unit of calorific value?
Answer:
The calorific value is defined as the amount of heat produced in calories (or joules) when one gram of the substance is completely burnt. The SI unit of calorific value is J kg-1. However, it is usually expressed in cal g-1.
![]()
Question 36.
Define enthalpy of neutralization.
Answer:
The heat of neutralisation is defined as “The change in enthalpy when one gram equivalent of an acid is completely neutralised by one gram equivalent of a base or vice versa in dilute solution”.
HCl(aq) + NaOH(aq) → NaCl(aq) + H2O1
∆H = – 57.32 kJ
Question 37.
What is lattice energy?
Answer:
Lattice energy is defined as the amount of energy required to completely remove the constituent ions from its crystal lattice to an infinite distance. It is also referred as lattice enthalpy.
Question 38.
What are state and path functions? Give two examples.
Answer:
State function:
A state function is a thermodynamic property of a system, which has a specific value for a given state and does not depend on the path (or manner) by which the particular state is reached.
Example:
Pressure (P), Volume (V), Temperature(T), Internal energy (U), Enthalpy (H), free energy (G) etc.
Path functions:
A path function is a thermodynamic property of the system whose value depends on the path by which the system changes from its initial to final states.
Example:
Work (w), Heat (q).
Question 39.
Give Kelvin statement of second law of thermodynamics.
Answer:
It is impossible to construct a machine that absorbs heat from a hot source and converts it completely into work by a cyclic process without transferring a part of heat to a cold sink.
Question 40.
The equilibrium constant of a reaction is 10, what will be the sign of ∆G? Will this reaction be spontaneous?
Answer:
∆G = -2.303 RT logKeq
Substituting the known values of R, T and Keq
R = 8.314(JK-1 mol-1)
T = 300 K
Keq = 10
∆G = –2.303 8.314(JK-1) 300(K) log 10
= -5744.14 J/mol
= -5.744 KJ/mol
∆G < 0, then it is spontaneous.
![]()
Question 41.
Enthalpy of neutralization is always a constant when a strong acid is neutralized by a strong base: account for the statement.
Answer:
It is because in dilution solution all strong acids and strong bases are completely ionized. The neutralization of strong acid and strong bases are completely ionized. The neutralization of a strong acid and strong base simply involves the combination of H+ ions (from acid) and OH– ions (from base) to form unionized water molecules with the evolution of 57.1 kJ heat.
H+(aq) + OH–(aq) → H2O(l),
∆2H° = -57.1 kJ
Since the same reaction takes place during neutralization of all strong acids and strong bases, the value of enthalpy of neutralization is constant.
Question 42.
State the third law of thermodynamics.
Answer:
The third law of thermodynamics states that the entropy of pure crystalline substance at absolute zero is zero. Otherwise it can be stated as it is impossible to lower the temperature of an object to absolute zero in a finite number of steps. Mathematically,
limT→0 S = 0 for a perfectly ordered crystalline state.
Question 43.
Write down the Born-Haber cycle for the formation of CaCl2.
Answer:
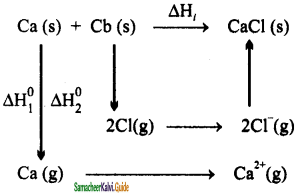
Step 1:
Solid calcium is converted to gaseous state (Enthalpy of atomization)
Ca(S) → Ca(g) Ca(g) ∆H°a = 178 KJ/mol
Step 2:
The calcium is converted to ionic form
(divalent cation): (Ionisation enthalpy)
Ca → Ca+ + e– ∆H°IE = 590 kJ
Ca → Ca2+ + e– ∆H°IE = 590 KJ
Step 3:
Atomisation of chlorine molecule to chlorine atom: (Atomisation enthalpy)
\(\frac{1}{2}\)Cl2 → Cl ∆H°Cl-Cl = 121 KJ
For two chlorine atoms required, atomistion energy = 2 × 121 = 242 KJ/mol
Step 4:
Convrsion of chlorine atom into ion:(Electron affinity)
Cl + e– → Cl–; ∆H°ea = – 364KJ
Step 5:
Finally the two ions join together by lattice energy as: (here two Cl– ions are involved)
Ca2+ + 2Cl– → CaCl2
Hence Lattice energy = Heat of formation – heat of atomization – dissociation energy – (sum of ionization energies) – (sum of electron affinities)
Since, heat of formation (i.e standard enthalpy of formation ) of CaCl2 = – 796KJ/mol
Lattice energy = -796 -178 -242 -(590 + 1145) – (2 × – 364) = -2223KJ/mol
Question 44.
Identify the state and path functions out of the following: (a) Enthalpy (b) Entropy (c) Heat (d) Temperature (e) Work (f) Free energy.
Answer:
State function:
Enthalpy, Temperature, Free energy, Entropy
Path function:
Work, Heat.
![]()
Question 45.
State the various statements of second law of thermodynamics.
Answer:
Entropy statement:
The second law of thermodynamics can be expressed in terms of entropy, i.e “the entropy of an isolated system increases during a spontaneous process”.
Kelvin-Planck statement:
It is impossible to construct a machine that absorbs heat from a hot source and converts it completely into work by a cyclic process without transferring a part of heat to a cold sink.
Clausius statement:
It is impossible to transfer heat from a cold reservoir to a hot reservoir without doing some work.
Question 46.
What are spontaneous reactions? What are the conditions for the spontaneity of a process?
Answer:
- A reaction that occurs under the given set of conditions without any external driving force is called a spontaneous reaction.
- The spontaneity of any process depends on three different factors.
- If the enthalpy change of a process is negative, then the process is exothermic and may be spontaneous. (∆H is negative)
- If the entropy change of a process is positive, then the process may occur spontaneously. (∆S is positive)
- The gibbs free energy which is the combination of the above two (∆H – T∆S) should be negative for a reaction to occur spontaneously, i.e. the necessary condition for a reaction to be spontaneous is ∆H – T∆S < 0
- For spontaneous process,
∆Stotal > 0, ∆G < 0, ∆S < 0
Question 47.
List the characteristics of internal energy.
Answer:
The internal energy of a system is an extensive property. It depends on the amount of the substances present in the system. If the amount is doubled, the internal energy is also doubled.
The internal energy of a system is a state function. It depends only upon the state variables (T, P, V, n) of the system. The change in internal energy does not depend on the path by which the final state is reached.
The change in internal energy of a system is expressed as ∆U = Uf – Ui.
In a cyclic process, there is no internal energy change. ∆U(cyclic) = 0
If the internal energy of the system in the final state (Uf) is less than the internal energy of the system in its initial state (Ui), then ∆U would be negative.
∆U = Uf – Ui = -ve(Uf < Ui)
If the internal energy of the system in the final state (Uf) is greater than the internal energy of the system in its initial state (Ui), then ∆U would be positive.
∆U = Uf – Ui = + ve(Uf > Ui).
Question 48.
Explain how heat absorbed at constant volume is measured using bomb calorimeter with a neat diagram.
Answer:
Calorimeter is used for measuring the amount of heat change in a chemical or physical change. In calorimetry, the temperature change in the process is measured which is directly proportional to the heat capacity. By using the expression C = \(\frac{q}{m \Delta T}\), we can calculate the amount of heat change in the process. Calorimetric measurements are made under two different conditions
(i) At constant volume (qV)
(ii) At constant pressure (qp)
(A) ∆U Measurements:
For chemical reactions, heat evolved at constant volume, is measured in a bomb calorimeter.
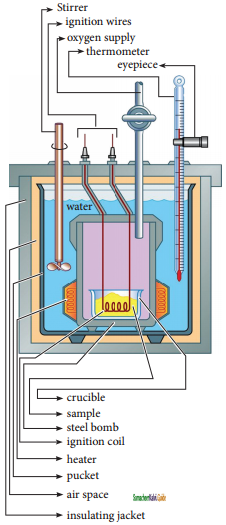
The inner vessel (the bomb) and its cover are made of strong steel. The cover is fitted tightly to the vessel by means of metal lid and screws.
A weighed amount of the substance is taken in a platinum cup connected with electrical wires for striking an arc instantly to kindle combustion. The bomb is then tightly closed and pressurized with excess oxygen. The bomb is immersed in water, in the inner volume of the calorimeter. A stirrer is placed in the space between the wall of the calorimeter and the bomb, so that water can be stirred, uniformly. The reaction is started by striking the substance through electrical heating.
A known amount of combustible substance is burnt in oxygen in the bomb. Heat evolved during the reaction is absorbed by the calorimeter as well as the water in which the bomb is immersed. The change in temperature is measured using a Beckman thermometer. Since the bomb is sealed its volume does not change and hence the heat measurements is equal to the heat of combustion at a constant volume (∆U)c.
The amount of heat produced in the reaction (∆U)c is, equal to the sum of the heat abosrbed by the calorimeter and water.
Heat absorbed by the calorimeter
q1 = k.∆T
where k is a calorimeter constant equal to mc Cc ( me is mass of the calorimeter and Cc is heat capacity of calorimeter)
Heat absorbed by the water q2 = mw Cw ∆T
where mw is molar mass of water
Cw is molar heat capacity of water (4,184 kJ K-1 mol-1)
Therefore ∆Uc = q1 + q2
= k.∆T + mw Cw ∆T
= (k + mw Cw)∆T
Calorimeter constant can be determined by burning a known mass of standard sample (benzoic acid) for which the heat of combustion is known (-3227 kJ mol-1). The enthalpy of combustion at constant pressure of the substance is calculated from the equation
∆H°c (pressure) = ∆U°c (Vol) + ∆ngRT
![]()
Question 49.
Calculate the work involved in expansion and 1 compression process.
Answer:
Work involved in expansion and compression processes:
In most thermodynamic calculations we are dealing with the evaluation of work involved in the expansion or compression of gases. The essential condition for expansion or compression of a system; is that there should be difference between external pressure (Pext) and internal pressure (Pint).
For understanding pressure-volume work, let us consider a cylinder which contains V moles of an ideal gas fitted with a frictionless piston of cross sectional area A. The total volume of the gas inside is V and pressure of the gas inside is Pint. If the external pressure Pext is greater than Pint, the piston moves inward till the pressure inside becomes equal to Pext. Let this change be achieved in a single step
and the final volume be Vf.In this case, the work is done on the system (+w). It can be calculated as follows
w = -F.∆x ……….(1)
where dx is the distance moved by the piston during the compression and F is the force acting on the gas.
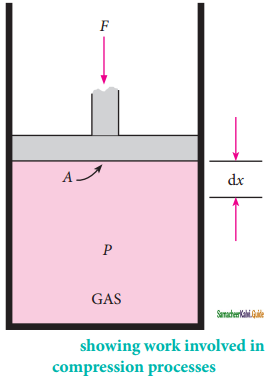
F = PextA ……….(2)
Substituting (2) in (1)
w = – Pext. A. ∆x
A .∆x = change in volume = Vf – Vi
w = -Pext.{Vf – Vi) ……….(3)
w = -Pext. (-∆V) …………(4)
= Pext.∆V
Since work is done on the system, it is a positive quantity.
If the pressure is not constant, but changes during the process such that it is always infinitesimally greater than the pressure of the gas, then, at each stage of compression, the volume decreases by an infinitesimal amount, dV. In such a case we can calculate the work donp on the gas by therelation
Wrev = – \(\int_{V_{i}}^{v_{f}}\) pext dV.
In a compression process, Pext the external pressure is always greater than the pressure of the system.
i.e., Pext = (Pint + dP)
In an expansion process, the external pressure is always less than the pressure of the system
i.e., Pext = (Pint – dP)
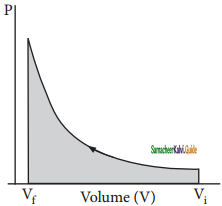
When pressure is not constant and changes in infinitesimally small steps (reversible conditions) during compression from Vi to Vf. the P-V plot looks like in figure. Work done on the gas is represented by the shaded area.
In general case we can write,
Pext = (Pint ± dP). Such processes are called reversible processes. For a compression process work can be related to internal pressure of the system under reversible conditions by writing equation
Wrev = – \(\int_{V_{i}}^{v_{f}}\) Pint dV
For a given system with an ideal gas
Pint V = nRT
pint = \(\frac{n R T}{V}\)
Wrev = – \(\int_{V_{i}}^{v_{f}}\) \(\frac{n R T}{V}\) dV
Wrev = – nRTln(\(\frac{V_{f}}{V_{i}}\))
Wrev= -2.303nRTlog\(\frac{V_{f}}{V_{i}}\) ………….(5)
If Vf > Vi (expansion), the sign of work done by the process is negative.
If Vf < Vi (compression) the sign of work done on the process is positive.
Question 50.
Derive the relation between ∆H and ∆U for an ideal gas. Explain each term involved in the equation.
Answer:
When the system at constant pressure undergoes changes from an initial state with H1, U1 and V1 to a final state with H2, U2 and V2 the change in enthalpy
∆H, can be calculated as follows:
H =U + PV
In the initial state
H1 = U1 + PV1 ………………(1)
In the final state
H2 = U2 + PV2 ……………..(2)
change in enthalpy is (2) – (1)
(H2 – H1) = (U2 – U1) + P(V2 – V1)
∆H = ∆U + P∆V ………………..(3)
As per first law of thermodynamics,
∆U = q + w
Equation (3) becomes
∆H = q + w+P∆V
w = -P∆V
∆H = qp – P∆V + P∆V
∆H = qp ………….(4)
qp – is the heat absorbed at constant pressure and is considered as heat content.
Consider a closed system of gases which are chemically reacting to form gaseous products at constant temperatureand pressure with Vi and Vf,as the total volumes of the reactant and product gases respectively, and niand nfas the number of moles of gaseous reactants and products, then,
For reactants (initial state):
PVi = niRT ………..(5)
For products (final state):
PVf = nfRT ……………..(6)
(6) – (5)
P{Vf – Vi) = (nf – ni)RT
P∆V = ∆n(g) RT ………..(7)
Substituting in (7) in (3)
∆H = ∆U+ ∆n(g)RT …………….(8)
![]()
Question 51.
Suggest and explain an indirect method to calculate lattice enthalpy of sodium chloride crystal.
Answer:
The formation of NaCl can be considered in five steps. The sum of the enthalpy changes of these steps is equal to the enthalpy change for the overall reaction from which the lattice enthalpy of NaCl is calculated.
Let us calculate the lattice energy of sodium chloride using Bom-Haber cycle
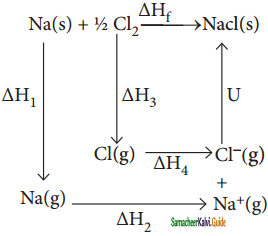
∆H = heat of formation of sodium chloride = -411.3 kJmol-1
∆H1 = heat of sublimation of Na(s) = 108.7 kJmol-1
∆H2 = ionisation energy of Na(s) = 495. kJ mol-1
∆H3 = dissociation energy of Cl2(g) = 244 kJ mol-1
∆H4 = Electron affinity of Cl(g) = -349 kJ mol-1
U = lattice energy of NaCl
∆Hf = ∆H1 + ∆H2 + ∆H3 + ∆H4 + U
∴ U = (∆Hf ) – (∆H1 + ∆H2 + \(\frac{1}{2}\)∆H3 + ∆H4)
=» U = (-411.3) – (108.7 + 495.0 + 122 – 349)
U = (-411.3) – (376.7)
∴ U = -788kJ mol-1
Question 52.
List the characteristics of Gibbs free energy.
Answer:
(i) G is defined as (H-TS) where H and S are the enthalpy and entropy of the system respectively. T = temperature. Since H and S are state functions, G is a state function.
(ii) G is an extensive property while ∆G = (G2 – G1) which is the free energy change between the initial (1) and final (2) states of the system becomes the intensive property when mass remains constant between initial and final states (or) when the system is a closed system.
(iii) G has a single value for the thermodynamic state of the system.
(iv) G and ∆G values correspond to the system only. There are three cases of ∆G in predicting the nature of the process. When, ∆G < 0 (negative), the process is spontaneous and feasible; ∆G = 0. The process is in equilibrium and ∆G > 0 (positive), the process is nonspontaneous and not feasible.
(v) ∆G = ∆H – T∆S. But according to I law of thermodynamics,
∆H = ∆G + P∆V and ∆U = q + w
∴ ∆G = q + w + P∆V – T∆S
But ∆S = \(\frac{T}{q}\) and T∆S = q = heat involved in the process.
∴ ∆G = q + w + P∆V – q = w + P∆V
(or) – ∆G = – w – P∆V = network.
The decrease in free energy – ∆G, accompanying a process taking place at constant temperature and pressure is equal to the maximum obtainable work from the system other than work of expansion.
This quantity is called as the “net work” of the system and it is equal to (- w – P∆V).
∴ Network = – w – P∆V
-∆G represents all others forms of work obtainable from the system such as electrical, chemical or surface work etc other than P-V work.
Question 53.
Calculate the work done when 2 moles of an ideal gas expands reversibly and isothermally from a volume of 500 ml to a volume of 2 L at 25°C and normal pressure.
Solution:
Given
n = 2 moles
Vi = 500 ml = 0.5 lit
Vf = 2 lit
T = 25°C = 298 K
w = -2303 nRTIog (\(\frac{V_{f}}{V_{i}}\))
w = -2.303 × 2 × 8.314 × 298 × log (4)
w = -2.303 × 2 × 8.314 × 298 × 0.6021
w = -6871 J
w = -6.871 kJ.
![]()
Question 54.
In a constant volume calorimeter, 3.5 g of a gas with molecular weight 28 was burnt in excess oxygen at 298 K. The temperature of the calorimeter was found to increase from 298 K to 298.45 K due to the combustion process. Given that the calorimeter constant is 2.5kJ K-1. Calculate the enthalpy of combustion of the gas in kJ mol-1.
Solution: Given
Ti = 298 K
Tf = 298.45 K
k = 2.5 kJ K-1
m = 3.5g
Mm = 28
heat evolved = k∆T
= k(Tf – Ti)
= 2.5KJ K-1 (298.45 – 298)K = 1.125 kJ
∆Hc = \(\frac{1.125}{3.5}\) × 28 kJ mol-1
∆Hc = 9 kJmol-1
Question 55.
Calculate the entropy change in the system, and surroundings, and the total entropy change in the universe during a process in which 245 J of heat flow out of the system at 77°C to the surrounding at 33°C.
Solution:
Given
Tsys = 77° C = (77 + 273) = 350 K
Tsurr = 33°C = (33 + 273) = 360 K
q = 245J
∆Ssys = \(\frac{q}{T_{s y}}=\frac{-245}{350}\) = -0.7 JK-1
∆Ssurr = \(\frac{q}{T_{s \mathrm{sr}}}=\frac{+245}{306}\) = +0.8 JK-1
∆Suniv = ∆Ssys + ∆Ssurr
∆Suniv = -0.7 JK-1 + 0.8 JK-1
∆Suniv = 0.1 JK-1
Question 56.
1 mole of an ideal gas, maintained at 4.1 atm and at a certain temperature, absorbs heat 3710/and expands to 2 litres. Calculate the entropy change in expansion process.
Solution:
Given
n = 1 mole
P = 4.1 atm
V = 2 Lit
T = ?
q = 3710 J
∆S = \(\frac{q}{T}\)
∆S = \(\frac{q}{\frac{p v}{n R}}\)
∆S = \(\frac{n R q}{P V}\)
∆S = \(\frac{1 \times 0.082 \text { lit atm } K^{-1} \times 3710 J}{4.1 \text { atm } \times 2 \text { lit }}\)
∆S = 37.10 JK-1
Question 57.
30.4 kJ is required to melt one mole of sodium chloride. The entropy change during melting is 28.4 JK-1 mol-1. Calculate the melting point of sodium chloride.
Answer:
Given,
∆Hf(NaCl) = 30.4 kJ = 30400 J mol-1
∆Sf(NaCl) = 28.4 JK-1 mol-1
∆S-1 = \(\frac{\Delta H_{f}}{T_{f}}\)
Tf = \(\frac{\Delta H_{f}}{\Delta S_{f}}\)
Tf = \(\frac{30400 J m o l^{-1}}{28.4 J K^{-1} m o l^{-1}}\)
Tf = 1070.4 K
![]()
Question 58.
Calculate the standard heat of formation of propane, if its heat of combustion is -2220.2 kJ mol-1. The heats of formation of CO2(g) and H2O(1) are -393.5 and -285.8 kJ mol-1 respectively.
Solution:
Given:
C3H8 + 5O2 → 3CO2 + 4H2O
∆H°C = 2220.2kJ mol-1 ……………..(1)
C + O2 → CO2
∆H°f = -393.5 kf mol-1 ……….(2)
H2 + \(\frac{1}{2}\)O2 → H2O
∆H°f = -285.8 kJ mol-1 ……………(3)
3C + 4H2 → C3H8
∆H°c =?
(2) × (3)
⇒ 3C + 3O2 → 3CO2
∆H°f = -1180.5 kJ ………..(4)
(3)× (4)
⇒ 4H2 + 2O2 → 4H2O
∆H°f = 1143.2 kJ ……..(5)
(4) + (5) – (1)
⇒ 3C + 3O2 + 4H2 + 2O2 + 3CO2 + 4H2O → 3CO2 + 4H2O + C3H8 + 5O2
∆H°f = -1180.5 – 1143.2 – (-2220.2) kJ
3C + 4H2 → C3H8
∆H°f = -103.5 kJ
Standard heat of formation of propane is ∆H°f(C3H8) = -103.5 kJ
Question 59.
You are given normal boiling points and standard enthalpies of vapourisation. Calculate the entropy of vapourisation of liquids listed below.
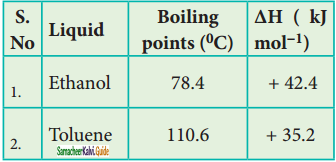
Answer:
For ethanol
Given:

Question 60.
For the reaction Ag2O(s) → 2Ag(s)+12O2(g) ∆H = 30.56 kJ mol-1 and ∆S = 6.66JK-1 mol-1 (at 1 atm). Calculate the temperature at which G is equal to zero. Also predict the direction of the reaction (I) at this temperature and (ii) below this temperature.
Solution:
Given,
∆H = 30.56 kJ mol-1
∆S = 6.66 x 10-3 kJK-1 mol-1
T = ? at which ∆G =0
∆G = ∆H – T∆S
0 = ∆H – T∆S
T = \(\frac{\Delta H}{\Delta S}\)
T = \(\frac{30.56 \mathrm{~kJ} \mathrm{~mol}^{-1}}{66.6 \times 10^{-3} \mathrm{~kJ} K^{-1} \mathrm{~mol}^{-1}}\)
T = 4589 K
(i) At 4589K;
∆G = 0 the reaction is in equilibrium.
(ii) at temperature below 4598 K
∆H > T∆S
∆G = ∆H – T∆S > 0, the reaction in the forward direction, is non spontaneous. In other words the reaction occurs in the backward direction.
![]()
Question 61.
What is the equilibrium constant Keq for the following reaction at 400K.
2NOCl(g) ⇌ 2NO(g) + Cl2(g), given that ∆H° = 77.2 kJ mol-1 ∆S° = 122 JK-1 mol-1
Answer:

Question 62.
Cyanamide (NH2CN) is completely burnt in excess oxygen in a bomb calorimeter, ∆U was found to be -742.4 kJ mol-1, calculate the enthalpy change of the reaction at 298K.
NH2CN(s) + \(\frac{3}{2}\)O2(g) → N2(g) + CO2(g) + H2O (l) ∆H = ?
Solution:
Given
T = 298 K;
∆U = -742.4 kJ mol-1
∆H =?
∆H = ∆U + ∆n(g)RT
∆H = ∆U + (np – nr)RT
∆H = 742.4 + 2 – \(\frac{3}{2}\) × 8.314 × 10-3 × 298
= -742.4 + (0.5 × 8.314 ×10-3 × 298)
=-742.4 + 1.24
= -741.16 kJ mol-1
Question 63.
Calculate the enthalpy of hydrogenation of ethylene from the following data. Bond energies of C – H, C – C, C = C and H – Hare 414, 347, 618 and 435 kJ mol-1.
Solution:
Given
EC-H= 414 kJ mol-1
EC-C= 347 kJ mol-1
EC-C= 6l8 kJ mol-1
EH-H = 435 kJ mol-1
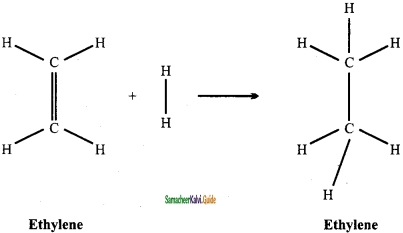
∆Hr = Σ(Bond energy)r – Σ(Bond energy)p
∆Hr = (EC=C + 4EC-H + EH-H) – (EC-C + 6EC-H)
∆Hr = (618 + (4 × 414) + 315) – (347 + (6 ×414))
∆Hr = 2709 – 2831
∆Hr = -122 kJ mol-1
Question 64.
Calculate the lattice energy of CaCl2 from the given data
Ca(s) + Cl2(g) → CaCl2(s) ∆H°f = – 795 kJ mol-1
Atomisation:
Ca(s) → Ca(g) ∆H°1 = -795 kJ mol-1
Ionisation:
Ca(g) → Ca2+(g) + 2e-1
∆H°2 = 2422 kJ mol-1
Dissociation:
Cl2(g) → 2Cl(g)
∆H°3 = + 242.8 kJ mol-1
Electron Affinity:
Cl(g) + e– → Cl-1
∆H°4 = -355 kJ mol-1
Answer:
∆Hf = ∆H1 + ∆H2 + ∆H3+∆H4 + u
-795 = 121 + 2422 + 242.8 + (2 × -355) + u
-795 = 2785.8 – 710 + u
-795 = 2075.8 + u
u = -795 – 2075.8
u = -2870.8 kJ mol-1
![]()
Question 65.
Calculate the enthalpy change for the reaction Fe203 + 3C0 – 2Fe + 3C02 from the following data.
2Fe + \(\frac{3}{2}\)O2 → Fe2O3; ∆H = -741 kJ
C + \(\frac{3}{2}\)O2 → CO; ∆H=-137kJ
C + O2 → CO2; ∆H = – 394.5 kJ
Answer:
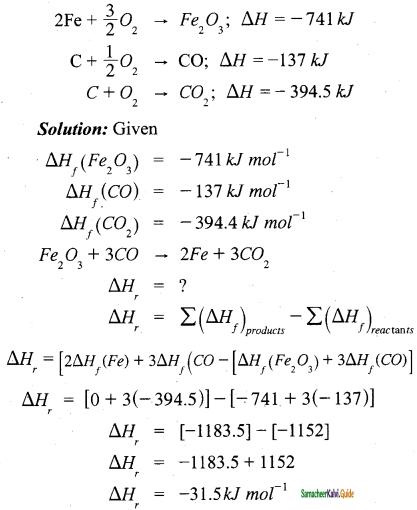
Question 66.
When 1-pentyne (A) is treated with 4N alcoholic KOH at 175°C, it is converted slowly into an equilibrium mixture of 1.3% 1-pentyne(A), 95.2% 2-pentyne(B), and 3.5% of 1,2 pentadiene (C) the equilibrium was maintained at 175°C, calculate ∆G° for the following equilibria.
B ⇌ A; ∆G°1 =?
B ⇌ C; ∆G°2 =?
Solution:
Given
T = 175°
C = 175 + 273 = 448 K
Concentration of 1-pentyne [A] = 1.3%
Concentration of 2-pentyne [B] = 95.2%
Concentration of 1, 2-pentadiene [C] = 3.5%
At equilibrium
B ⇌ A
95.2% 1.3% ⇒
B ⇌ C
95.2% 3.5% ⇒
K2 = \(\frac{3.5}{95.2}\) = 0.0367
⇒ ∆G°1 = -2.303 RTlogK
∆G°1 = – 2.303 × 8.314 × 448 × log 0.0136
∆G°1 = +16010 J
∆G°1 = +16 kJ
⇒ ∆G°2 = – 2.303 RT log K2
∆ G°2 = -2.303 × 8.314 × 448 × log 0.0367
∆ G°2 = +12312J
∆G°2 = +12.312 kJ
Question 67.
At 33K, N2O4 is fifty percent dissociated. Calculate the standard free energy change at this temperature and at one atmosphere.
Solution:
Given
T= 33 K
N2O4 ⇌ 2NO2
Initial concentration: 100% 0
Concentration dissociated 50% – Concentration remaining at equilibrium 50% 100%
Keq = \(\frac{100}{50}\) = 2
∆G° = -2.303 RT log Keq
∆G°= -2.303 × 8.314 × 33 × log 2
∆G° = -190.18 Jmol-1
Question 68.
The standard enthalpies of formation of SO2 and SO3 are – 297 kJ mol-1 and – 396 kJ mol-1 respectively. Calculate the standard enthalpy of reaction for the reaction: SO +4-0 — SO
Solution:
Given
∆H°f(SO2) = – 297 kJ mol-1
∆H°f(SO3) = – 396 kJ mol-1
SO2 + 12O2 → SO3;
∆H°r =?
∆H°r = (∆H°f)compound – Σ( ∆Hf)elements
∆H°r =∆H°r(SO3) – ∆H°f
∆H°r = 396 kJ mol-1– (- 297 kJ mol-1 + 0)
∆H°r = – 396 kJ mol-1 + 297
∆H°r = -99 kJ mol-1
Question 69.
For the reaction at 298 K: 2A + B → C
∆H = 400 Jmol-1; ∆S = 0.2 JK∆ mol-1 Determine the temperature at which the reaction would be spontaneous.
Solution:
Given,
T = 298 ∆T
∆H = 400 J mol-1 = 400 J mol-1
∆S = 0.2 JK-1 mol-1
∆G = ∆H – T∆S
if T = 2000 K
∆G = 400 – (0.2 × 2000) = 0
if T > 2000 K
∆G will be negative. The reaction would be spontaneous only beyond 2000 K
Question 70.
Find out the value of equilibrium constant for the following reaction at 298K,
2NH3 + CO2 ⇌ NH2CONH2 (aq) + H2O (l) Standard Gibbs energy change, ∆G°r at the given temperature is -13.6 kJ mol-1.
Solution:
Given:
T = 298 K
∆G°r = -13.6 kJ mol-1
= – 13600 J mol-1
∆G° = – 2.303 RT log Keq
log Keq = \(\frac{-\Delta G^{0}}{2.303 R T}\)
log Keq = \(\frac{13.6 \mathrm{~kJ} \mathrm{~mol}^{-1}}{2.303 \times 8.314 \times 10^{-3} \mathrm{JK}^{-1} \mathrm{~mol}^{-1} \times 298 \mathrm{~K}}\)
log Keq = 2.38
Keq = antilog (2.38)
Keq = 239.88
![]()
Question 71.
A gas mixture of 3.67 lit of ethylene and methane on complete combustion at 25°C and at 1 atm pressure produce 6.11 lit of carbondioxide. Find out the amount of heat evolved in kJ, during this combustion. (∆HC(CH4)) = -890 kJmol-1 and ∆HC(C2H4) = -1423 kJ mol-1
Solution:
Given
∆HC(CH4) = – 890 kJ mol-1
∆HC(C2H4) = -1423 kJ mol-1
Let the mixture contain x lit of CH4 and (3.67 – x) lit of ethylene.
CH4 + 2O2 → CO + 2H2O
x lit x lit
C2H4 + 3O2 → 2 CO2 + 2H2O
(3.67 -x) lit 2 (3.67 -x) lit
Volume of Carbondioxide formed = x + 2(3.67 – x) = 6.11 lit
x + 7.34 – 2x = 6.11
7.34 – x = 6.11
x = 1.23 lit
Given mixture contains 1.23 lit of methane and 2.44 lit of ethylene, hence
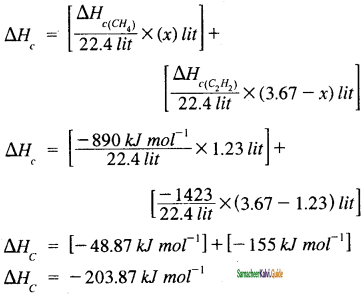
11th Chemistry Guide Thermodynamics Additional Questions and Answers
I. Choose the best answer:
Question 1.
_______is a part of universe which is separated from the rest of the universe by real or imaginary boundaries.
(a) Surroundings
(b) boundary
(c) system
(d) matter
Answer:
(c) system
Question 2.
Which one of the following is a closed system?
(a) Hot water in a closed beaker
(b) Hot water in a thermos flask
(c) Hot water in a open beaker
(d) Chemical reactions
Answer:
(a) Hot water in a closed beaker
Question 3.
Which of the following is/are extensive properties?
1. volume
2. Surface tension
3. mass
4. internal energy
(a) 1, 2 and 4
(b) 1, 3 and 4
(c) 1 and 3
(d) 1, 2 and 3
Answer:
(b) 1, 3 and 4
Question 4.
Which of the following is/are intensive properties?
1. refractive index
2. density
3. number of moles
4. molar volume
(a) 1, 2 and 4
(b) 1, 3 and 4
(c) 1, 2 and 3
(d) 2, 3 and 4
Answer:
(b) 1, 3 and 4
Question 5.
For an isothermal process _______.
(a) dT = 0
(b) dV = 0
(c) dq = 0
(d) dP = 0
Answer:
(a) dT = 0
![]()
Question 6.
Which of the following is/are state function?
1. Pressure
2. work
3. internal energy
4. Free energy
5. heat
(a) 1, 2 and 4
(b) 1, 3 and 4
(e) 1, 2 and 3
(d)2, 3 and 4
Answer:
(b) 1, 3 and 4
Question 7.
Which of the following is/are path function?
1. pressure
2. work
3. internal energy
4. Free energy
5. heat
(a) 1, 2 and 4
(b) 1, 3 and 4
(c) 2 and 5
(d) 2, 3 and 4
Answer:
(c) 2 and 5
Question 8.
Which is the correct about internal energy, U?
(a) It is an extensive property
(b) It is a state function
(c) For a cyclic process. ∆U = 0.
(d) Change in internal energy is ∆U = Ui – Uf
Answer:
(a) It is an extensive property
Question 9.
Work done by’ a given system with an ideal gas in a reversible process is wrev =
(a) – nRln (Vf/Vi)
(b) – nRTln (Vi/Vf)
(c) – nRTln (Vf/Vi)
(d) – nTln (Vf/Vi)
Answer:
(c) – nRTln (Vf/Vi)
Question 10.
For a cyclic process involving isothermal expansion of an ideal gas
(a) ∆U = 0
(b) ∆U = q
(c) ∆U = q + w
(d) ∆U = q – w
Answer:
(a) ∆U = 0
![]()
Question 11.
Choose the correct statement about enthalpy
(a) Enthalpy is a path function
(b) Enthalpy change ∆H = ∆U + V∆P
(c) In an endothermic process, ∆H = 0.
(d) In an exothermic process. ∆H is negative
Answer:
(d) In an exothermic process. ∆H is negative
Question 12.
Which ofthc following reactions correctly indicates the process of atomization?
(a) CH4 → CH3(g) + H(g)
(b) CH4(g) → CH(g) + 4H(g)
(c) CH(g) + O2(g) → CO2(g)
(d) N2(g) + 3H2(g) → 2NN3(g)
Answer:
(b) CH4(g) → CH(g) + 4H(g)
Question 13.
A reaction has both H and S negative. The rate of reaction
(a) increases with increase of temperature
(b) increases with decrease of temperature
(e) remains unaffected by change of temperature
(d) cannot be predicted for change in temperature
Answer:
(b) increases with decrease of temperature
Question 14.
Evaporation of water is
(a) an exothermic change
(b) an endothermic change
(e) a process where no heat changes occur
(d) a process accompanied by chemical reaction
Answer:
(b) an endothermic change
Question 15.
The entropy change for a non spontaneous reaction is 140 JK-1 mol at 298 K. The reaction is
(a) reversible
(b) irreversible
(c) exothermic
(d) endothermic
Answer:
(d) endothermic
![]()
Question 16.
The enthalpy and entropy change for the reaction: Br2(l) +Cl2(g) → 2BrCl(g) are 30 kJ mol-1 and 105 kJ mol-1 respectively. The temperature at which the reaction will be in
equilibrium is
(a) 300 K
(b) 285.7 K
(c) 273 K
(d) 450 K
Answer:
(b) 285.7 K
Question 17.
Three moles ofan ideal gas expanded spontaneously into vaccum. The work done will be
(a) Infinite
(b) 3 JouIes
(c) 9 Joules
(d) zero
Answer:
(d) zero
Question 18.
If the enthalpy change for the transition of liquid water to steam is 30 kJ mol-1 at 27°C, the entropy change for the process would be
(a) 10 J mol-1K-1
(b) 1.0 J mol-1K-1
(c) 0.1 J mol-1K-1
(d) 100 J mol-1K-1
Answer:
(d) 100 J mol-1K-1
Question 19.
Enthalpy change for the reaction,
4H(g) → 2H2(g) is – 869.6 kJ
The dissociation energy of H-H bond is
(a) -434.8 kJ
(b) -869.6 kJ
(c) + 434.8 kJ
(d) +217.4 kJ
Answer:
(c) + 434.8 kJ
Question 20.
Which of the following is correct option for free expansion of an ideal gas under adiabatic condition?
(a) q = 0, ∆T ≠ 0, w = 0
(b) q ≠ 0, ∆T = 0, w = 0
(c) q = 0, ∆T = 0, w = 0
(d) q = 0, ∆T < 0, w ≠ 0
Answer:
(b) q ≠ 0, ∆T = 0, w = 0
![]()
Question 21.
The total entropy change for a system and its surroundings increases, if the process is
(a) reversible
(b) irreversible
(c) exothermic
(d) endothermic
Answer:
(b) irreversible
Question 22.
∆S is positive for the change
(a) mixing of two gases
(b) boiling of liquid
(c) melting of solid
(d) all of these
Answer:
(d) all of these
Question 23.
If w1, w2, w3 and w4 are work done in isothermal, adiabatic, isobaric and isochoric reversible processes, the correct order (for expansion) will be
(a) w1 > w2 > w3 > w4
(b) w3 > w2 > w1 > w4
(c) w3 > w2 > w4 > w1
(d) w3 > w1 > w2 > w4
Answer:
(d) w3 > w1 > w2 > w4
Question 24.
The subject matter of thermodynamics comprises
(a) energy transformations in a system
(b) mass changes in molecular reactions
(c) total energy of system
(d) rates of chemical reactions
Answer:
(a) energy transformations in a system
Question 25.
A hydrogen bond is very useful in determining the structures and properties of compounds. Its energy varies between
(a) 12 – 20 kJ /mol
(b) 50 – 100 kJ/mol
(c) 10 – 100 kJ/mol
(d) 75 – 200 kJ/mol
Answer:
(c) 10 – 100 kJ/mol
![]()
Question 26.
In which of the enlisted cases, Hess’s law is not applicable?
(a) Determination of lattice energy
(b) Determination of resonance energy
(c) Determination of enthalpy of transformation of one allotropic form to another
(d) Dtermination of entropy
Answer:
(d) Dtermination of entropy
Question 27.
The amount of energy required to completely remove the constituent ions from its crystal lattice to an infinite distance is called
(a) lattice energy
(b) ionization energy
(c) internal energy
(d) free energy
Answer:
(a) lattice energy
Question 28.
Statement -1:
The allotropes of carbon, namely, graphite and diamond differ each other.
Statement -2:
They possess different internal energies and have different structures.
In the above statement/s
(a) 1 alone is correct
(b) 2 alone is correct
(c) both 1 and 2 are correct
(d) both 1 and 2 are incorrect
Answer:
(c) both 1 and 2 are correct
Question 29.
Which of the following statement is incorrect? According to thermodynamics, work
(a) is a path function
(b) appears only at the boundary of the system
(c) appears during the change in the state of the system.
(d) surroundings is so large that macroscopic changes occurs in the surroundings
Answer:
(d) surroundings is so large that macroscopic changes occurs in the surroundings
Question 30.
The work done by a force of one Newton through a displacement of one meter is called
(a) joule
(b) calorie
(c) erg
(d) tesla
Answer:
(a) joule
![]()
Question 31.
The enthalpy of neutralization of strong acid vs strong base is approximately equal to ________(in kJ).
(a) 57.32
(b) – 57.32
(c) 5.98
(d) – 5.98
Answer:
(b) – 57.32
Question 32.
The maximum efficiency of an automobile engine working between the temperatures 816°C and 21°C is
(a) 73 %
(b) 45%
(c) 67%
(d) 78%
Answer:
(b) 45%
Question 33.
A reaction that occurs under the given set of conditions without any external driving force is called a reaction.
(a) Reversible
(b) spontaneous
(c) irrversible
(d) cyclic
Answer:
(b) spontaneous
Question 34.
Which one of the following spontaneous reaction is endothermic?
(a) combustion of methane
(b) dissolution of ammonium nitrate
(c) acid-base neutralization reaction
(d) none of the above
Answer:
(b) dissolution of ammonium nitrate
Question 35.
The available energy in the system to do work is called
(a) Gibbs free energy
(b) internal energy
(c) potential energy
(d) kinetic energy
Answer:
(a) Gibbs free energy
![]()
Question 36.
Which one of the following is incorrect about Gibbs free energy?
(a) Extensive property
(b) path function
(c) ∆G < 0 for a spontaneous process (d) ∆G > 0 for a non-spontaneous process
Answer:
(b) path function
Question 37.
Match the following:
| (A) Adiabatic | (i) dp = 0 |
| (B) Isothermal | (ii) dV = 0 |
| (C) Isobaric | (iii) dq = 0 |
| (D) Isochoric | (iv) dT = 0 |
(a) A – iii, B – iv, C – i, D – ii
(b) A – ii, B – iv, C – iii, D – i
(c) A – iv, B – iii, C – i, D – ii
(d) A – i, B – iv, C – ii, D – iii
Answer:
(a) A – iii, B – iv, C – i, D – ii
Question 38.
For a cyclic process involving isothermal expansion of an ideal gas, q =
(a) 0
(b) P∆V
(c) w
(d) – w
Answer:
(d) – w
Question 39.
In Calorimeter, the expression used to calculate the amount of heat change in the process is
(a) C = qm∆T
(b) C = m/q∆T
(c) C = q/m∆T
(d) C = q∆T/m
Answer:
(c) C = q/m∆T
Question 40.
“It is impossible to transfer heat from a cold reservoir to a hot reservoir without doing some work”. This statement is given by
(a) Clausius
(b) Kelvin
(c) Gibbs
(d) Joule
Answer:
(a) Clausius
![]()
II. Very short question and answers (2 Marks):
Question 1.
Define isolated system.
Answer:
A system which can exchange neither matter nor energy with its surroundings is called an isolated system. Here boundary is sealed and insulated.
Question 2.
What is a homogeneous system? Give an example.
Answer:
A system is called homogeneous if the physical state of all its constituents is the same. Example: a mixture of gases.
Question 3.
Illustrate Closed system with an example.
Answer:
Hot water contained in a closed beaker is an example for a closed system. In this system energy (heat) is transferred to the surroundings but no matter (water vapour) can escape from this system. A gas contained in a cylinder fitted with a piston constitutes a closed system.
Question 4.
Define irreversible process.
Answer:
The process in which the system and surrounding cannot be restored to the initial state from the final state is called an irreversible process. All the processes occurring in nature are irreversible processes.
Question 5.
Define standard entropy change.
Answer:
The absolute entropy of a substance at 298 K and one bar pressure is called the standard entropy S°.
![]()
Question 6.
What is Zeroth law of thermodynamics?
Answer:
The law states that’ If two systems are separately in thermal equilibrium with a third one, then they tends to be in thermal equilibrium with themselves’.
Question 7.
Define enthalpy.
Answer:
The enthalpy (H), is a thermodynamic property of a system, is defined as the sum of the internal energy (U) of a system and the product of pressure and volume of the system.
H = U + PV
Question 8.
Define specific heat capacity of a system.
Answer:
The heat absorbed by one kilogram of a substance to raise its temperature by one Kelvin at a specified temperature.
Question 9.
What is a reversible process?
Answer:
The process in which the system and surrounding can be restored to the initial state from the final state without producing any changes in the thermodynamic properties of the universe is called a reversible process.
Question 10.
What is a thermodynamic process? Give two examples.
Answer:
The method of operation which can bring about a change in the system is called thermodynamic process.
Examples: Heating, Cooling, expansion.
![]()
Question 11.
Distinguish between state function and path function.
Answer:
A state function is a thermodynamic property of a system, which has a specific value for a given state and does not depend on the path by which the particular state is reached. A path function is a thermodynamic property of the system whose value depends on the path by which the system changes from its initial to final states.
Question 12.
Write any two characteristics of internal energy.
Answer:
- The internal energy of a system is an extensive property.
- The internal energy of a system is a state function.
Question 13.
Write the importance of internal energy.
Answer:
The internal energy possessed by a substance differentiates its physical structure. For example, the allotropes of carbon, namely, graphite C (graphite) and diamond C (diamond), differ from each other because they possess different internal energies and have different structures.
Question 14.
Write notes on heat.
Answer:
The heat (q) is regarded as an energy in transit across the boundary separating a system from its surrounding. Heat changes lead to temperature differences between system and surrounding. Heat is a path function.
Question 15.
Write the thermodynamic significance of work.
Answer:
The work
- is a path function.
- appears only at the boundary of the system.
- appears during the change in the state of the system.
- in thermodynamics, surroundings is so large that macroscopic changes to surroundings do not happen.
![]()
Question 16.
What is meant by pressure-volume work?
Answer:
In elementary thermodynamics the only type of work generally considered is the work done in expansion (or compression) of a gas. This is known as pressure-volume work, PV work or expansion work.
Question 17.
What is specific heat capacity of a system?
Answer:
The heat absorbed by one kilogram of a substance to raise its temperature by one Kelvin at a specified temperature is called specific heat capacity of a system.
Question 18.
Distinguish between Cv and Cp.
Answer:
The molar heat capacity at constant volume (Cv) is defined as the rate of change of internal energy with respect to temperature at constant volume. The molar heat capacity at constant pressure (Cp) can be defined as the rate of change of enthalpy with respect to temperature at constant pressure.
![]()
III. Short Question and Answers (3 Marks):
Question 1.
What is internal energy?
Answer:
The internal energy of a system is equal to the energy possessed by all its constituents namely atoms, ions and molecules. The total energy of all molecules in a system is equal to the sum of their translational energy (Ut), vibrational energy (Uv), rotational energy (Ur), bond energy (Ub), electronic energy (Ue) and energy due to molecular interactions (Ui).
Thus:
U = Ut + Uv + Ur + Ub + Ue + Ui
The total energy of all the molecules of the system is called internal energy.
Question 2.
Give applications of bomb calorimeter.
Answer:
- Bomb calorimeter is used to determine the amount of heat released in combustion reaction.
- It is used to determine the calorific value of food.
- Bomb calorimeter is used in many industries such as metabolic study, food processing, explosive testing etc.
Question 3.
What is Molar heat of fusion?
Answer:
The molar heat of fusion is defined as “the change in enthalpy when one mole of a solid substance is converted into the liquid state at its melting point”.
For example, the heat of fusion of ice
H2O(s) → H2O(l)
∆H(fusion) = +5.98 kJ
![]()
Question 4.
Write any three statements of first law of thermodynamics.
Answer:
- Whenever an energy of a particular type disappears, an equivalent amount of another type must be produced.
- The total energy of a system and surrounding remains constant (or conserved)
- “Energy can neither be created nor destroyed, but may be converted from one form to another”.
Question 5.
Describe the need for the second law of thermodynamics.
Answer:
From the first law of thermodynamics, the energy of the universe is conserved. Let us consider the following processes:
A glass of hot water over time loses heat energy to the surrounding and becqmes cold.
When you mix hydrochloric acid with sodium hydroxide, it forms sodium chloride and water with evolution of heat.
In both these processes, the total energy is conserved and are consistent with the first law of thermodynamics. However, the reverse process i.e. cold water becoming hot water by absorbing heat from surrounding on its own does not occur spontaneously even though the energy change involved in this process is also consistent with the first law. However, if the heat energy is supplied to cold water, then it will become hot. i.e. the change that does not occur spontaneously and an be driven by supplying energy.
Question 6.
Write notes on entropy statement of second law of thermodynamics.
Answer:
The second law of thermodynamics can be expressed in terms of entropy, i.e “the entropy of an isolated system increases during a spontaneous process”.
For an irreversible process such as spontaneous expansion of a gas,
Stotal > 0
Stotal > Ssystem + Ssurrounding
i.e., Suniverse > Ssystem + Ssurrounding
For a reversible process such as melting of ice,
Ssystem = Ssurrounding
Suniverse = 0
![]()
IV. Long Question and Answers(5 Marks):
Question 1.
Explain steps to write thermochemical equations.
Answer:
A thermochemical equation is a balanced stoichiometric chemical equation that includes the enthalpy change (∆H). The following conventions are adopted in thermochemical equations:
- The coefficients in a balanced thermochemical equation refer to number of moles of reactants and products involved in the reaction.
- The enthalpy change of the reaction ∆Hr has to be specified with appropriate sign and unit.
- When the chemical reaction is reversed, the value of ∆H is reversed in sign with the same magnitude.
- The physical states (gas, liquid, aqueous, solid in brackets) of all species are important and must be specified in a thermochemical reaction, since ∆H depends on the physical state of reactants and products.
- If the thermochemical equation is multiplied throughout by a number, the enthalpy change is also multiplied by the same number.
- The negative sign of ∆Hr indicates that the reaction is exothermic and the positive sign of ∆Hr indicates an endothermic reaction.