Students can download Maths Chapter 3 Algebra Ex 3.5 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.5
Question 1.
Simplify
(i) \(\frac{4 x^{2} y}{2 z^{2}} \times \frac{6 x z^{3}}{20 y^{4}}\)
Answer:
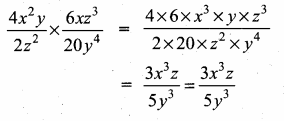
![]()
(ii) \(\frac{p^{2}-10 p+21}{p-7} \times \frac{p^{2}+p-12}{(p-3)^{2}}\)
Answer:
P2 – 10p + 21 = (p – 7) (p – 3)
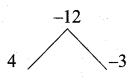
p2 + p – 12 = (p + 4) (p – 3)
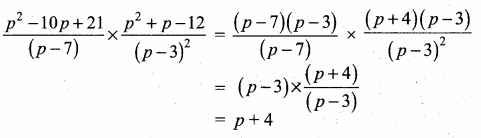
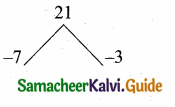
(iii) \(\frac{5 t^{3}}{4 t-8} \times \frac{6 t-12}{10 t}\)
Answer:
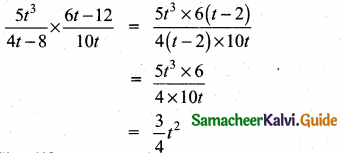
![]()
Question 2.
Simplify
(i) \(\frac{x+4}{3 x+4 y} \times \frac{9 x^{2}-16 y^{2}}{2 x^{2}+3 x-20}\)
Answer:
9x2 – 16y2 = (3x)2 – (4y)2
= (3x + 4y) (3x – 4y)
2x2 + 3x – 20 = 2x2 + 8x – 5x – 20
= 2x (x + 4) – 5 (x + 4)
= (x + 4) (2x – 5)
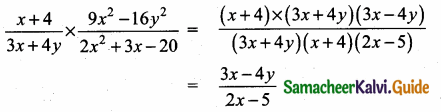
(ii) \(\frac{x^{3}-y^{3}}{3 x^{2}+9 x y+6 y^{2}} \times \frac{x^{2}+2 x y+y^{2}}{x^{2}-y^{2}}\)
Answer:
x3 – y3 = (x – y) (x2 + xy + y2)
x2 + 2xy + y2 = (x + y) (x + y)
3x2 + 9xy + 6y2 = 3(x2 + 3xy + 2y2)
= 3 (x + 2y) (x + y)
(x2 – y2) = (x + y) (x – y)
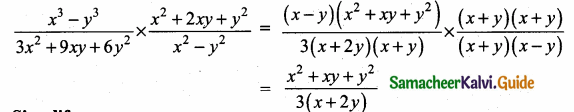
![]()
Question 3.
Simplify
(i) \(\frac{2 a^{2}+5 a+3}{2 a^{2}+7 a+6} \div \frac{a^{2}+6 a+5}{-5 a^{2}-35 a-50}\)
Answer:
2 a2 + 5a + 3a + 3 = 2a2 + 2a + 3a + 3
= 2a(a + 1) + 3 (a + 1)
= (a + 1) (2a + 3)
2a2 + 7a + 6 = 2a2 + 3a + 4a + 6
= a(2a + 3) + 2 (2a + 3)
= (2a + 3) (a + 2)
a2 + 6a + 5 = (a + 5) + (a + 1)
-5a2 – 35a – 50 = -5(a2 + 7a + 10)
= -5(a + 5)(a + 2)
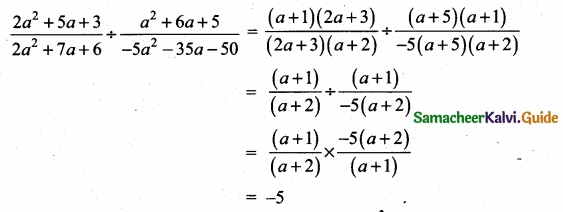
![]()
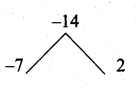
(ii) \(\frac{b^{2}+3 b-28}{b^{2}+4 b+4}+\frac{b^{2}-49}{b^{2}-5 b-14}\)
Solution:
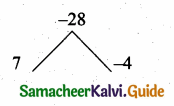
b2 + 3b – 28 = (b + 7) (b – 4)
b2 + 4b + 4 = (b + 2) (b + 2)
b2 – 49 = b2 – 72
= (b + 7) (b – 7)
b2 – 5b – 14 = (b – 7) (b + 2)

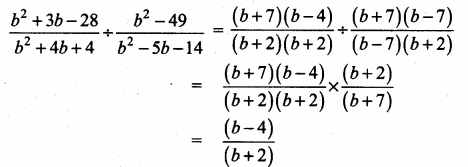
(iii) \(\frac{x+2}{4 y}+\frac{x^{2}-x-6}{12 y^{2}}\)
Answer:
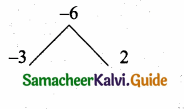
x2 – x – 6 = (x – 3) (x + 2)
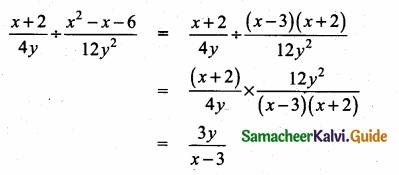
![]()
(iv) \(\frac{12 t^{2}-22 t+8}{3 t} \div \frac{3 t^{2}+2 t-8}{2 t^{2}+4 t}\)
Answer:
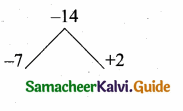
12t2 – 22t + 8 = 2(6t2 – 11t + 4)
= 2[6t2 – 8t – 3t + 4]
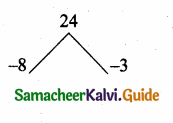
= 2[2t (3t – 4) – 1 (3t – 4)]
= 2(3t – 4) (2t – 1)
3t2 + 2t – 8 = 3t2 + 6t – 4t – 8
= 3t(t + 2) – 4 (t + 2)
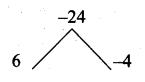
= (t + 2) (3t – 4)
2t2 + 4t = 2t(t + 2)
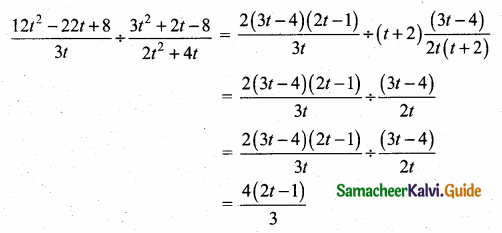
![]()
Question 4.
If x = \(\frac{a^{2}+3 a-4}{3 a^{2}-3}\) and y = \(\frac{a^{2}+2 a-8}{2 a^{2}-2 a-4}\) find the value of x2y-2
Answer:
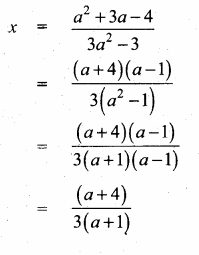

The value of x2 y-2 = \(\frac{x^{2}}{y^{2}}\) = (\(\frac { x }{ y } \))2

![]()
Question 5.
If a polynomial p(x) = x2 – 5x – 14 when divided by another polynomial q(x) gets reduced to \(\frac { x-7 }{ x+2 } \) find q(x).
Answer:
p(x) = x2 – 5x – 14
= (x – 7) (x + 2)
By the given data
\(\frac { p(x) }{ q(x) } \) = \(\frac { (x-7) }{ x+2 } \)
\(\frac{(x-7)(x+2)}{q(x)}\) = \(\frac { (x-7) }{ x+2 } \)
q(x) × (x – 7) = (x – 7) (x + 2) (x + 2)
q(x) = \(\frac{(x-7)(x+2)(x+2)}{(x-7)}\)
= (x + 2)2
q(x) = x2 + 4x + 4